永磁同步电动机参数在线辨识的无位置传感器控制

杨灵艺,　王忠庆

(中北大学 电气与控制工程学院，太原 030051)

0　引　言

随着不断提升的永磁材料性能和日益成熟电力电子技术，永磁同步电机由于其具有高效率、高转动惯量比、体积小等优势，在相关领域的应用越来越广泛[1-3]。

近年来，为满足实际需求实现永磁同步电动机(PMSM)的无位置传感器控制，提出了很多方法，主要分为两类：一类方法是基于电机基频估计数学模型的直接的方法[4-7]，其优点是相对容易实现，但在低速和零速时，基本的电压、电流信号检测困难。另一类方法，即利用电机的凸极性估计[8，9]，避免了电机参数的影响，但是由于电机运行过程中需要不断的注入信号，降低了逆变器的电压利用率，信号处理的复杂程度限制了此类方法的动态性能。

为了保证电机在不同阶段运行状态的控制效果，近几年，学者们广泛研究了将参数辨识应用到无位置传感器控制系统中。其中，文献[10]中采用模型参考自适应系统实现无位置传感器控制技术，并利用扩展卡尔曼滤波器法(Extended Kalman filter,EKF)对转子磁链在同步旋转坐标系下的分量进行了在线辨识，避免了外加信号的注入。文献[11]在文献[10]的基础上分析了在不同转速下转子磁链和交轴电感对电机控制的影响，实现了多参数的辨识反馈，调速过程平稳。但是，两者都用到了低通滤波器，增加了系统运算的复杂性。在文献[12]中，采用高频注入法估算转子位置，将辨识参数应用于模型自适应方法的PMSM无传感器控制，但误差较大。文献[13]中建立了递归最小二乘法的参数辨识模型, 实时辨识出了对电机的d、q轴电感,并将辨识结果应用于对转子的位置观测，但是此方法并不适用于电机的零速启动。文献[14]中改进了模型参考自适应系统，但是不适用于无位置传感器控制。

在上述研究的基础上，本文提出了一种改进的EKF方法来实现PMSM的无位置传感器控制。在此基础上建立了模型参考自适应模型在线辨识参数，补偿了由于电机的低阶状态方程而引起的转子磁链辨识问题，提高了电机动态与稳态过程的稳定性。最后，利用 MATLAB/Simulink进行仿真，验证所提出的方案的有效性。

1　PMSM无位置传感器的实现

EKF是一种非线性估计，它能有效地抑制系统和测量误差的影响，提高状态估计的精度，并能快速准确地估计状态变量的值，收敛速度较快[15]。

1.1　PMSM的EKF数学模型

在PMSM的控制中，通常采用id=0的矢量控制方法，以最小的电流幅值保证得到最大的输出转矩。并作出以下假设：定子三相绕组对称分布，气隙磁动势和磁通的基波为正弦分布，并且不计铁心饱和，忽略涡流以及磁滞损耗。此时电机在dq轴的数学模型可以表示为：

(1)

式中:id、iq和ud、uq分别为dq轴电流和电压；Ld、Lq为电机dq电感；pm为电机的极对数；ωm为转子的机械角速度；Te、TL分别为电磁转矩与负载转矩；Bv为阻尼系数；J为转动惯量；ψr为转子磁链。

根据Park变换以及Clark变换，可以得出αβ坐标系下电机的磁链方程为：

(2)

对于表面式PMSM来说，d轴电感与q轴电感有Ld=Lq=L，磁链的表达式为：

(3)

又两相静止坐标系下电压方程为：

(4)

将式(1)代入式(2)得电压方程的另一种表达式：

(5)

αβ坐标系下电机的电磁转矩方程为：

Te=1.5pmψr(iβcosθ-iαsinθ)

(6)

将式(5)用电流方式表达可得：

(7)

式中:iα、iβ和uα、uβ分别为α、β轴电流和电压;R和L分别为电机的定子电阻和定子电感;ψr为转子磁链;ω为电机的转速;θ为转子位置角。

选取状态变量x和输入量u：

x=[iαiβωθ]T，u=[uαuβ]T

则系统对应的非线性方程为：

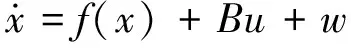
系统的测量方程为：

y=h(x)+ν

其中:w、ν分别为系统噪声与量测噪声，且

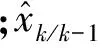
1.2　无位置传感器控制系统

EKF用于估计PMSM的转子位置时，电机的随机参数对估计结果有很大的影响。因此，研究这些参数的影响对提高估计结果的准确性具有重要意义。本文在1.1分析的基础上，得出了基于EKF的无位置传感器PMSM系统的结构框图，如图1所示。仿真时采用的电机参数如下：额定电压220 V，额定电流2.5 A，极对数3，定子电阻0.6 Ω，d轴电感6．8 mH，q轴电感17． 2 mH，转子磁链0.178 Wb，转动惯量1.44×10 kg·m2。

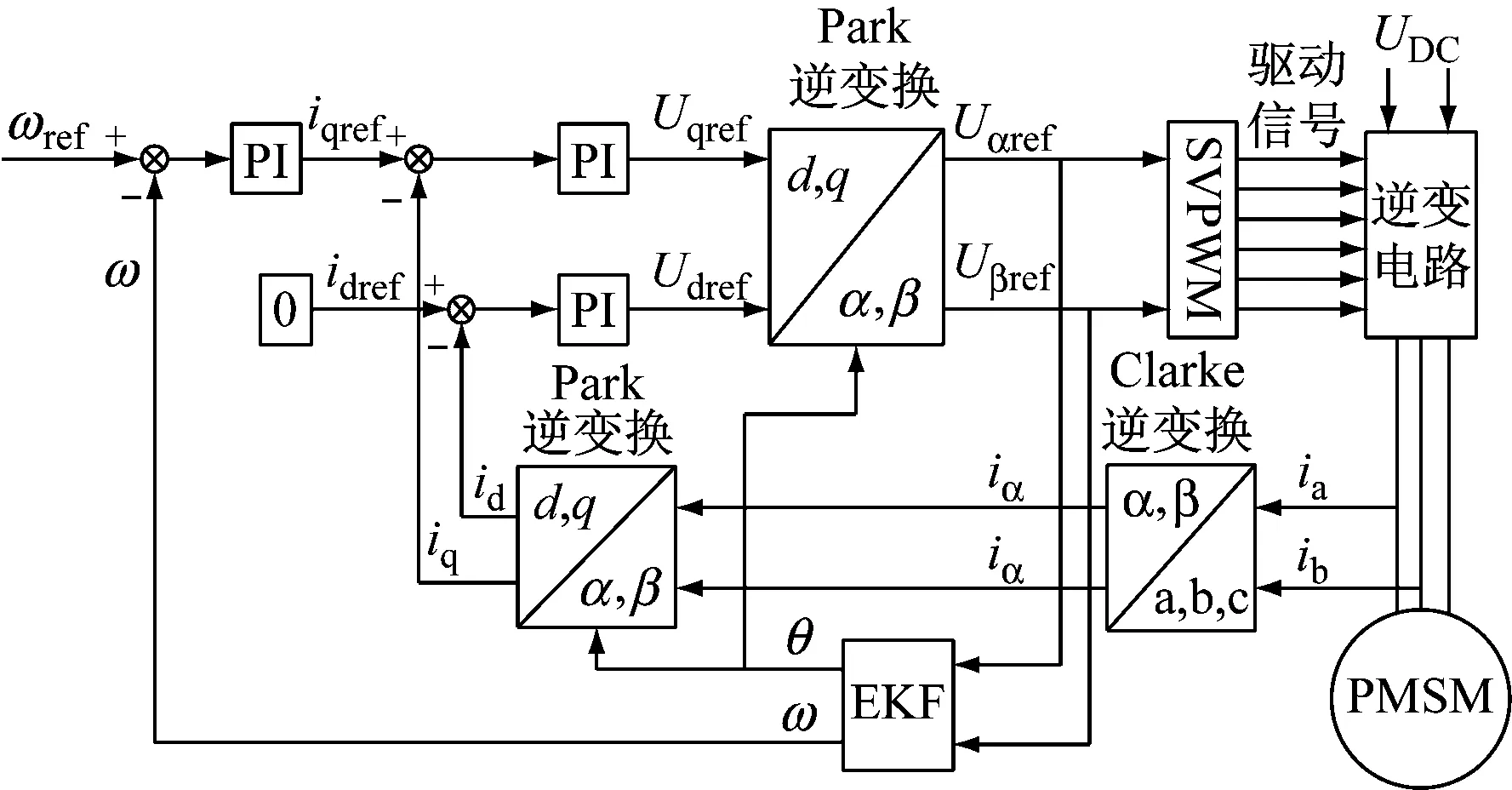
图1无位置传感器系统结构图

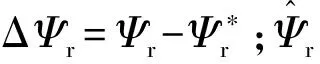
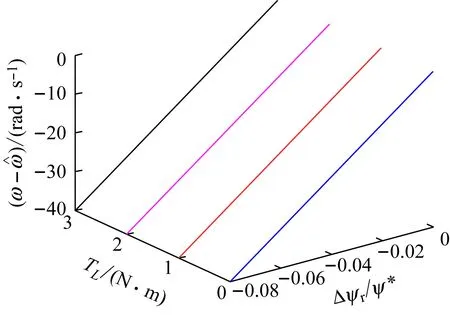
图2　转速估计偏差与负载及转子磁链偏差关系图

2　仿真和试验验证

2.1　基于MARS的扩展卡尔曼滤波器在线修正

由上述研究可知，当采用EKF模型对电机位置估计时，转子磁链参数的依赖性较大。为了提高无传感器模式下的估算精度，本文采用模型参考自适应的方法对转子磁链辨识，以更新EKF模型，从而提高估算精度。

PMSM的d-q坐标系状态方程可描述为：

(13)

式中:

假设PMSM定子电阻R和电感L已知，转速ω恒定且已知，PMSM转子磁链Ψr的辨识模型如下：

[8]阿兰·罗伯-格里耶：《理论有什么用》，《快照集/为了一种新小说》，余中先译，长沙：湖南美术出版社，2001年，第74页。

(14)

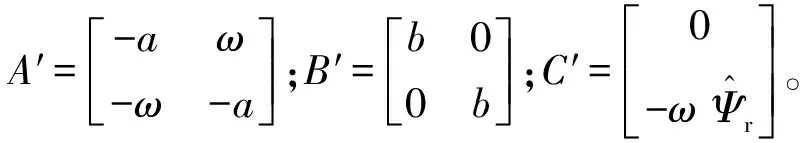
将ψr的辨识模型式(14)减去方程(13),得:

(15)

令

(16)

根据Popov超稳定理论，要使上述系统稳定，则要求下列条件成立：① 线性定常环节严格正实； ② 非线性时变环节满足Popov积分不等式。

(17)

式中，Kh1、Kh2均为正数。

利用Matlab/Simulink构建出PMSM转子磁链的自适应辨识仿真模型，得到仿真结果如图3，由图得出，基于模型参考自适应方法对转子磁链的辨识时间短，辨识结果能够很快达到收敛。

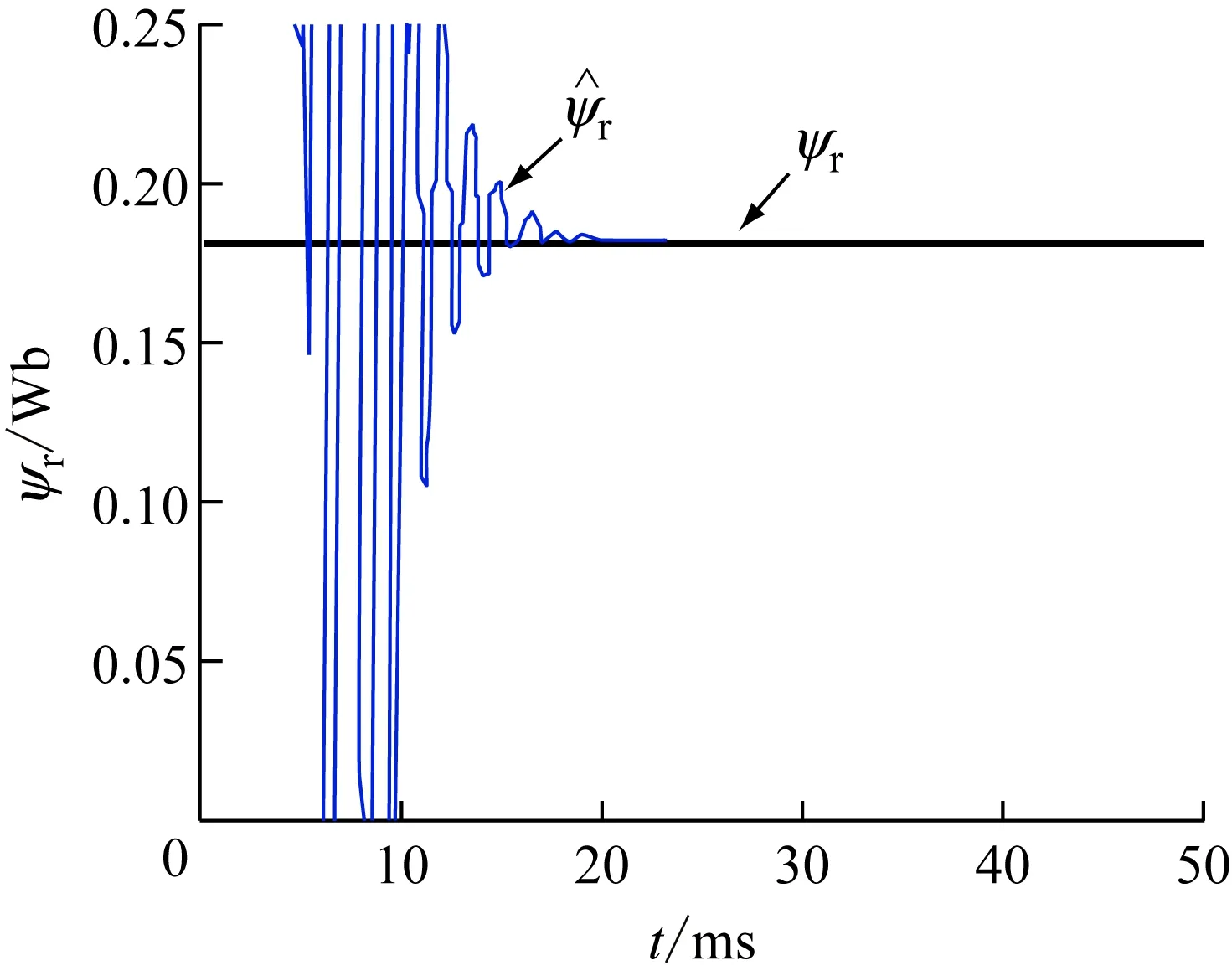
图3　转子磁链的辨识曲线

仿真时，将电机参数的实际值应用于EKF模型中，而在40 ms时改变电机参数，此时减小10%的转子永磁磁链，分别增大和减小15%的定子电阻与定子电感。与EKF模型使用原来的电机参数的估算进行对比，此时估计结果出现了较大的偏差，如图4所示。当在60 ms时刻时将辨识出的参数反馈到EKF滤波器时，及时更新了EKF模型中的电机参数，随后的估计偏差明显降低，如图4所示。

图4带参数辨识的EKF仿真结果

2.2　实验结果

本文搭建的实验平台采用ST公司16位定点处理器TMS320LF2407A作为控制芯片，采用Lattice公司的CPLD芯片ispLSI1032E实现逻辑译码、数据锁存以及多路开关功能，系统时钟设置为48 MHz，功率模块的开关频率设定为8 kHz。PMSM从零速时刻起动运行到1 000 r/min，无传感器位置和速度估计性能和在线参数辨识性能如图5～6所示(A点表示200 mV点)。其中：图5为EKF估计的测量结果，可见，通过传感器和EKF估算得到的转速和位置。图6为由模型参考自适应电机永磁磁链曲线线辨识结果，辨识得到的磁链平均为0.191Wb，具有较好的稳定性，且接近于实际值0.178Wb，两者的误差仅0.7%，验证了辨识方法的有效性。将模型参考自适应辨识得到的永磁磁链参数实时应用到EKF系统中用于电机转速和位置的估算，得到较好的控制效果。

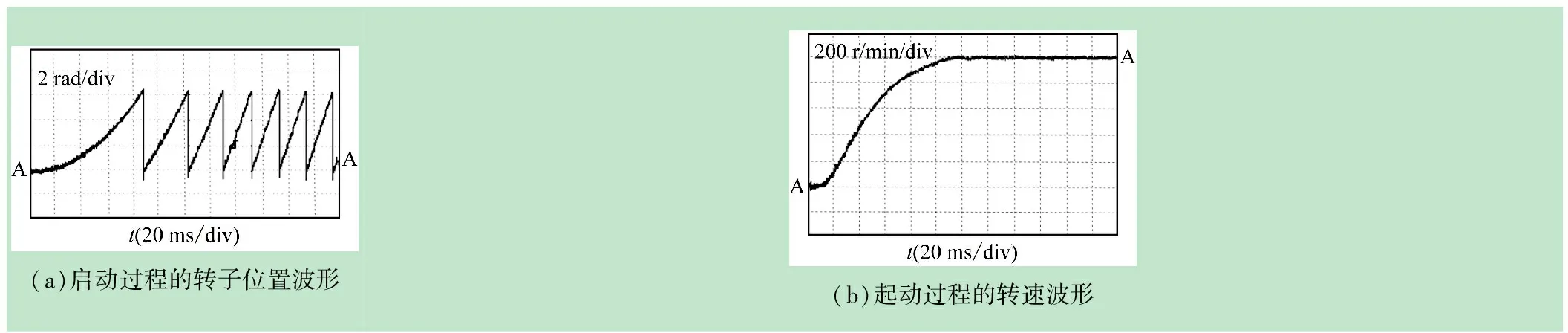
图5EKF估算的的实测结果

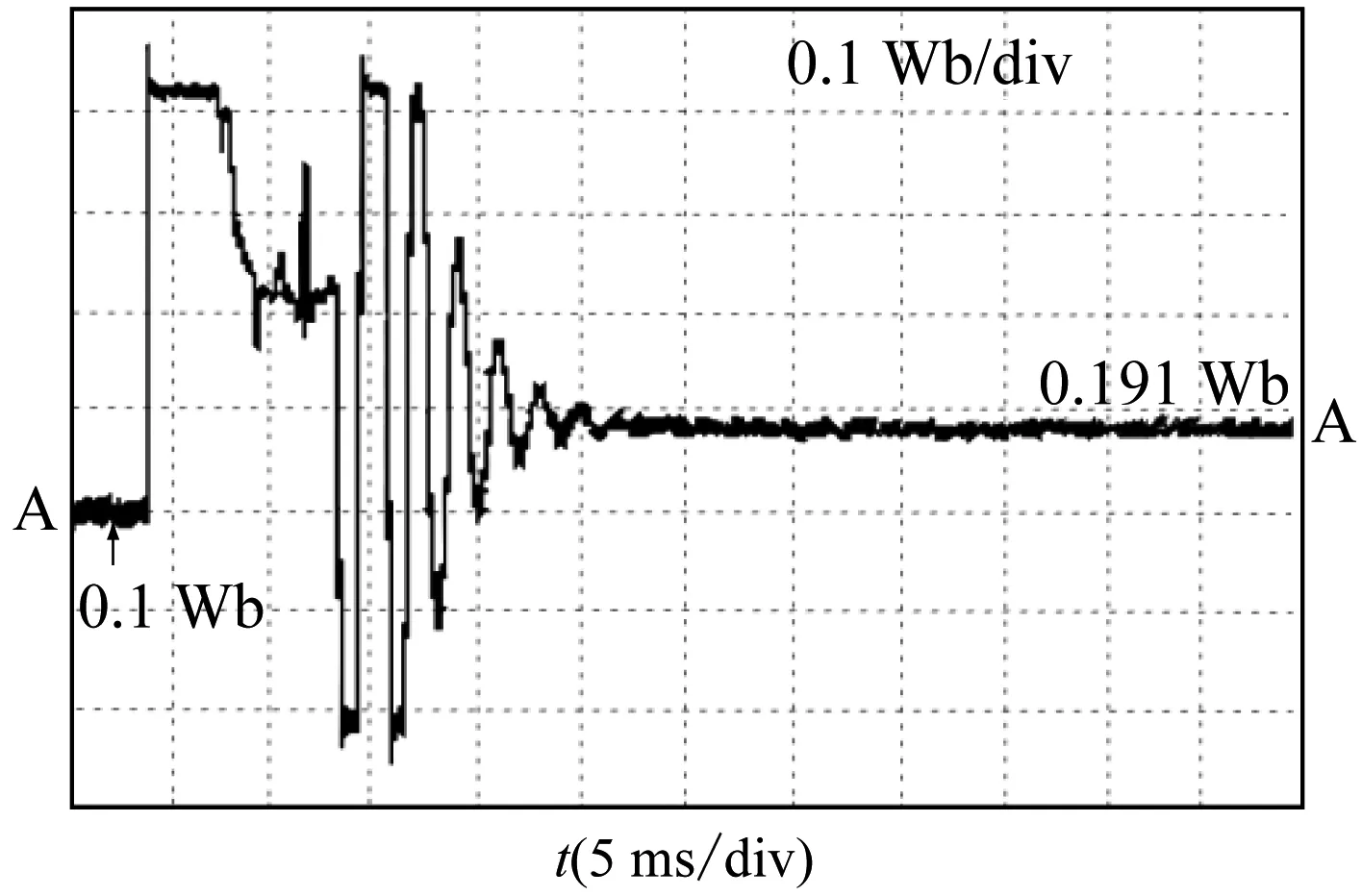
图6转子磁链的辨识结果

3　结　语

本文改进了应用于无位置传感器PMSM系统，从电机的实际模型出发，考虑了实际的转动惯量，减小了在模型假设下“无穷大转动惯量”对滤波器跟随性能的影响。在此基础上，根据Popov超稳定理论出发和电机模型，设计了转子磁链的自适应辨识律。实现了对永磁磁链的在线辨识，误差为0.7%。仿真和实验证明，该方法使电机从零速时刻起动运行到1 000 r/min的时间约为25 ms，能够快速收敛到真实值，对基于EKF模型的的转子磁链参数进行了实时修正，对EKF的估算效果进行有效的补偿。

参考文献(References)：

[1]卢东斌,欧阳明高,谷靖,等. 电动汽车永磁同步电机最优制动能量回馈控制[J]. 中国电机工程学报,2013(3):83-91，12.

[2]Chen Xing, Hu Jibin, Chen Kai, Peng Zengxiong. Modeling of electromagnetic torque considering saturation and magnetic field harmonics in permanent magnet synchronous motor for HEV[J]. Simulation Modelling Practice and Theory,2016(10):256-261.

[3]孙静,张承慧,刘旭东,等. 基于Hamilton系统理论的电动汽车用永磁同步电机H_∞控制[J]. 电工技术学报,2013,(11):163-169.

[4]Li Biao，Li Chuan. Position sensorless control of permanent magnet synchronous motor based on high performance flux estimation algorithm[J]. Transactions of China Electrotechnical Society, 2016，31(11)：59-67.

[5]Wang Xiaodong, Liu Gang.Sensorless control of high speed permanent magnet synchronous motor based on modified sliding-mode observer Source[J]. Energy Research and Power Engineering, 2014，986：1134-1137.

[6]Shi Yuchao, Sun Kai, Ma Hongyan. Permanent magnet flux identification of IPMSM based on EKF with speed sensorless control[C]∥Conference of the IEEE Industrial Electronics Society, Singapore, 2010:2252-2257.

[7]Zhao Xiangheng, Yang Wu, Wang Minhuai.Direct torque control of speed sensorless permanent magnet synchronous motor based on MARS[J]. Journal of Central South University, 2015,46(10)：3631-3636.

[8]高宏伟,于艳君,柴凤,等. 基于载波频率成分法的内置式永磁同步电机无位置传感器控制[J]. 中国电机工程学报,2010(18):91-96.

[9]Wang Jianmin, Gao Jianwei. Analysis of position estimation error resulted from filter in carrier signal injection based sensorless control of PMSM[C]∥International Conference on Electrical Machines and Systems, 2011:1-6.

[10]Shi Yuchao, Sun Kai, Huang Lipei,etal. Online identification of permanent magnet flux based onextended Kalman filter for IPMSM drive with position sensorless control[J]. IEEE Transactions on Industrial Electronics, 2012,59(11): 4169-4178.

[11]李旭春,张鹏,严乐阳,等. 具有参数辨识的永磁同步电机无位置传感器控制[J]. 电工技术学报,2016(14):139-147,164.

[12]张红. 无位置传感器控制下的永磁同步电机在线参数辨识[J]. 微特电机,2016(6):66-69.

[13]年珩,李嘉文,万中奇. 基于参数在线辨识的永磁风力发电机无位置传感器控制技术[J]. 中国电机工程学报,2012(12):146-154.

[14 ]Liu Hongzhang ,Chen Shijun, Cao Hui. The parameters identification of PMSM based on model reference adaptive[J]. International Conference on Consumer Electronics,2012: 687-689.

[15]安群涛,孙力,李波. 永磁同步电动机转速的变参数EKF估算方法[J]. 电机与控制学报,2007(6):559-563.