满足公平性约束的云任务调度QoS算法
2018-04-11刘雨潇
刘雨潇, 王 毅, 袁 磊, 吴 钊
(湖北文理学院 数学与计算机科学学院, 湖北 襄阳 441053)
0 引 言
大多数大规模科学应用通常表现为复杂的科学工作流形式,包含了一个通过数据依赖性连接而成的有序任务集合[1]。工作流调度系统即是使用具体的调度策略实现可用云资源与工作流任务间的映射,并满足用户需求[2]。传统的工作流调度环境多为静态的,即资源可用性在保持不变的情况下进行工作流任务的调度。作为最新兴的计算模式,云计算可以按即付即用和按需提供的方式提供各种互联网资源[3],因此,云资源的计算性能和可用状态是动态变化的,该环境下的工作流调度将更为复杂。本文将设计一种动态自适应的工作流调度算法,通过寻找动态的关键路径,从而动态地以更低的调度开销降低整个工作流的执行跨度。
目前,云工作流调度问题已经成为云计算领域中的研究热点。相关研究中,文献[4]中提出的HEFT是一种异构最快完成时间工作流调度算法,旨在通过赋予任务不同的优先级,最小化工作流的总调度时间。文献[5]中提出基于遗传算法GA的调度算法,将染色体表示为任务资源映射方案,同时表示任务执行序列,算法根据最优化目标对个体进行进化,并基于约束目标进化种群,但算法的进化代数过多,可能无法找到可行解。文献[6]中提出一种基于动态规划的云工作流调度算法,有效解决了资源价格变化环境中任务调度的开销优化问题。文献[7]中提出Fussy-PSO算法尝试使用粒子群优化PSO算法实现工作流调度时执行跨度与执行代价的均衡。以上算法在进行任务映射时,其针对的对象多为静态行为的资源,没有考虑资源使用本身的动态性,可能导致任务调度的开销过大。
基于关键路径的启发式算法是解决工作流依赖任务间调度问题的有效手段,其目标是寻找任务DAG中所有执行路径中的最长路径(关键路径),从而得到整个工作流的最小执行跨度[8]。显然,在单个任务被调度后,关键路径会发生动态变化,而传统的动态关键路径调度算法仅仅实现了同质环境中的任务与资源映射问题,即调度方案仅在任务DAG中计算一次。由于云计算环境是动态异构环境,本文的目标即是扩展传统的动态关键路径以适应于云工作流的动态调度环境。
1 工作流调度问题
通常,工作流应用以有向无循环图(Directed Acyclic Graph,DAG)表示,图的节点表示工作流任务,图的边表示任务间的依赖性,节点权重表示任务计算复杂性,边的权重则表示任务间的通信数据量。因此,工作流调度问题通常可视为一种DAG调度问题,为NP完全问题。
令W(T,E)表示云工作流,T表示工作流任务集,T={T1,T2,…,Tx,…,Ty,Tn},E表示任务间依赖关系集,E={
2 CWS-DCP算法设计
在工作流任务DAG中,单个任务的开始时间的下限与上限可分别表示为绝对最早开始时间AEST和绝对最晚开始时间ALST。传统的动态关键路径算法中,由于关键任务的延迟会影响任务DAG的整体执行时间,因此,处于关键路径上的任务拥有相同的AEST和ALST。处于关键路径上的第一个任务首先被调度,直至所有任务被调度完成为止。然而,以上的调度方法仅适用于调度资源不受限且不考虑计算和通信时间的环境,云计算提供的计算、存储、带宽资源拥有不同的能力和可用性,是异构动态环境,因此,笔者作了如下几点改进:
(1) 对于单个任务,其初始AEST和ALST由为该任务提供最小执行时间的资源计算得到,总体目标是降低每次通过的关键路径的长度;
(2) 为了实现关键路径上的任务映射,所有可用的云资源均被考虑进来,由于在异构云环境中资源的可用性会发生变化,而通信与计算时间会受此影响;
(3) 当任务映射至资源时,其执行时间和与父任务间的数据传输时间进行实时更新,这会改变后续任务的AEST和ALST。
为了便于CWS-DCP算法的描述,表1给出了文中相关的符号及其含义说明。
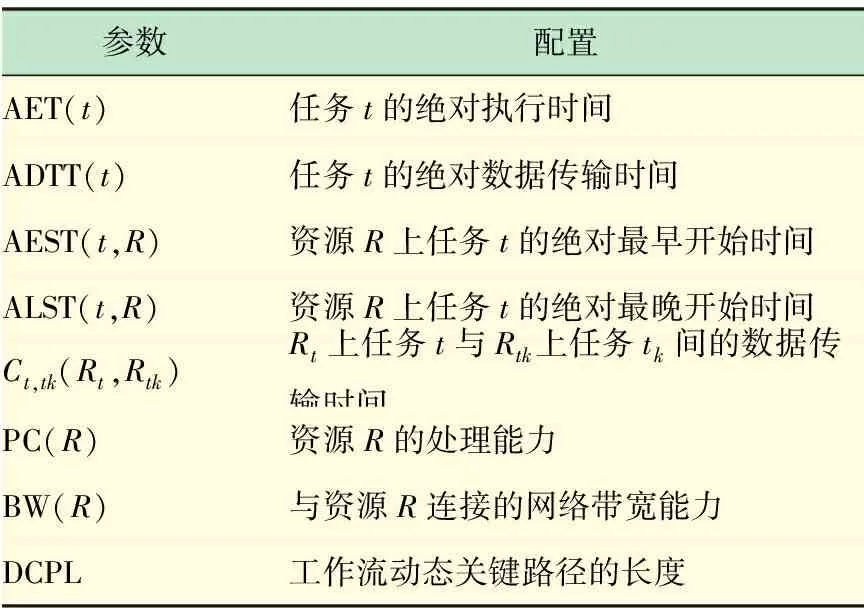
表1 符号说明
2.1 AEST和ALST计算
CWS-DCP算法中,任务的开始时间直到被映射至资源上才被确定下来。此时,引入两个属性:任务的绝对执行时间AET和绝对数据传输时间ADTT,AET表示任务的最小执行时间,ADTT表示在当前部署状态下传输任务输出数据的最小时间。初始状态下,AET和ADTT的计算方法为:
(1)
(2)
式中:PC(Rk)表示资源Rk的处理能力,BW(Rk)表示资源Rk的传输能力(带宽)。
当任务t调度至资源时,AET(t)和ADTT(t)根据式(1)、式(2)进行更新。因此,资源R上任务t的AEST可表示为AEST(t,R),以递归形式表示为:
AEST(t,R)=MAX1≤k≤p{AEST(tk,Rtk)+
AET(tk)+Ct,tk(Rt,Rtk)}
(3)
式中:t拥有p个父任务,tk表示第k个父任务,且:
(1) 如果t为入口任务,则AEST(t,R)=0;
(2) 如果Rt=Rtk,则Ct,tk(Rt,Rtk)=0;
(3) 如果t和tk未被调度,则Ct,tk(Rt,Rtk)=ADTT(tk)。
此时,如果两个任务被调度至相同资源,则其通信时间等于0,如果子任务仍未被调度,则其通信时间等于父任务的ADTT。利用以上定义,AEST可以通过从入口任务开始以宽度优先方式遍历任务DAG的方式计算AEST。
计算所有任务的AEST后,可以计算动态关键路径长度DCPL,即部分已映射工作流的调度长度(时间),定义为:
DCPL=MAX1≤i≤n{AEST(ti,Rti)+AET(ti)}
(4)
式中:n表示工作流的任务总数量。
计算DCPL后,ALST可以通过反向宽度优先方式遍历任务DAG的方式计算得到。因此,资源R上任务t的ALST可表示为ALST(t,R),以递归形式表示为:
ALST(t,R)=MIN1≤k≤c{ALST(tk,Rtk)-
AET(t)-Ct,tk(Rt,Rtk)}
(5)
式中:t拥有c个子任务,tk表示第k个子任务,且:
(1) 如果t为出口任务,则ALST(t,R)=DCPL-AET(t);
(2) 如果Rt=Rtk,则Ct,tk(Rt,Rtk)=0;
(3) 如果t和tk未被调度,Ct,tk(Rt,Rtk)=ADTT(tk)。
2.2 任务与资源选择
任务调度过程中,任务DAG的关键路径决定了部分调度工作流的调度长度,因此,必须赋予关键路径上的任务优先级。然而,随着调度过程的进行,关键路径是动态变化的,即:由于资源行为的动态变化可能导致在当前步骤中关键路径上的任务在下一步骤中可能不是关键路径上的任务。因此,在云计算环境中,工作流的关键路径是动态可变的。
动态关键路径上的任务有着相同的开始时间上限和下限,即相同的AEST和ALSP。因此,如果任务的AEST和ALST是相同的,则动态关键路径的任务也在关键路径上,称为关键任务。为了降低每一步中的DCPL,调度过程中选择的任务需要处于关键路径上,且不存在未被映射的父任务,即:选择的为拥有最低AEST的关键路径。
确定关键任务后,需要为任务选择合适资源。此时选择的资源是为任务提供最小执行时间的资源。该过程可以通过遍历所有可用资源,寻找在相同资源上关键子任务的最小开始时间的任务,该子任务即为关键任务所有子任务中拥有最小的AEST与ALST之差的任务。最后,关键任务被映射至能够提供最早开始时间的资源上。
2.3 算法步骤
以下伪代码给出了CWS-DCP算法的具体执行过程。
1.Input:WorkflowW(T,E),TashDependencyList,
Resource SetR
2.Output: Mappling Strategy
3.for allt∈Tof workflowW
4.compute AET and ADTT fort
5.end for
6.for allt∈Tof workflowW
7.compute AEST for r running BFS
8.end for
9.compute DCPL
10.for allt∈Tof workflowW
11.compute ALST fortrunning BFS following reverse
task dependency
12.end for
13.while all tasks inTare not completed do
14.TaskList←Get unscheduled Ready tasks for workflowW
15.Schedule Tash(TaskList,R)
16.Update TaskDependencyList
17.end while
18.Schedule Task
19.Input: TaskList, Resource SetR
20.while TaskList is not empty do
21.Tct←Get critical task from all tasks of TaskList
22.Tctc←Get critical chile task from all child task ofTct
23.r←Get a resource from R that can provide earliest start time for bothTctandTctc
24.scheduleTctonr
25.update status ofr
26.for allt∈Tof workflowW
27.compute AEST fortrunning BFS
28.end for
29.cmpute DCPL
30.for allt∈Tof workflowW
31.compute ALST fortrunning BFS following reverse
task dependency
32.end for
33.end while
算法说明:首先,CWS-DCP算法计算所有任务的初始AET、ADTT、AEST和ALST,然后,选择AEST与ALST之差最小的任务,并通过选择拥有最小AEST的任务切断与前驱任务的连接。根据之前的讨论,处于动态关键路径DCP上的该任务即为关键任务。关键任务的关键子任务也通过这种方式确定。然后,算法计算关键任务在所有可用资源上的开始时间(同时考虑了其所有父任务的完成时间),选择为任务tct和其关键子任务提供了最早开始时间的资源作为目标资源。
选择合适资源R之后,算法计算开始时间AEST(tct,R)和在该资源上任务tct的持续时间AET(tct),并更新任务tct的实际开始时间和执行时间。其他任务的AEST和ALST在每次调度的结束进行更新,以决定下一个关键任务。该过程进行至工作流中所有任务被调度时结束。
2.4 算例说明
为了进一步说明CWS-DCP算法的思想,图1给出了以CWS-DCP算法进行工作流任务调度的算例过程。样本工作流由五个任务组成,表示为{T0,T1,T2,T3,T4},各任务拥有不同的执行时间和数据传输需求。图1(a)给出了每个任务的大小和输出数据的大小,分别表示为百万指令数(Million Instruction,MI)和GB,任务被调度至两个云资源R1和R2,其处理能力表示为PC,传输能力表示为BW(带宽),如图1所示。
算例说明:首先,图1(a)计算每个任务的AET和ADTT,然后,使用以上得到的值,计算所有任务的AEST和ALST,如图1(b)所示。由于T0、T2、T3和T4拥有相同的AEST和ALST,则这4个任务均在关键路径上,且T0作为最高任务。由于选择T0作为关键任务并被映射至R1,故R1带给T0最小开始时间。该步骤完成后,可以计算此时工作流的调度长度DCPL为890。类似地,图1(c)中,选择T2作为关键任务并被映射至R1。由于T0和T2均被映射至R1,T0的数据传输时间此时为0,所有任务的AEST和ALST均发生改变,工作流的调度长DCPL变为850,如图1(d)。在下一步,T3被映射至R1,由于T2的数据传输时间为0,因此DCPL减少至770。
当前,T4是唯一处于关键路径上的任务,如图1(e)。然而,T4的子任务之一T1仍然没有被映射,因此,选择T1作为关键任务。由于T2和T3已经被映射至R1,R1上T1的开始时间为700,故在R2上其开始和结束时间分别为180和430,T1被映射至R2。最后,当T4映射至R1时(图1(g)),所有任务已被映射,工作流的调度长度DCPL无法进一步改进,得到最终DCPL为750。由CWS-DCP得到的最终调度方案如图1(h)所示。

图1算例说明
3 性能评估
为了评估CWS-DCP算法的性能,利用CloudSim[9]构建云工作流调度环境,并建立了不同类型的工作流模型与同类型算法进行性能比较。
3.1 工作流模型
为了模拟产生不同格式不同权重的工作流模型,实验中将以下参数作为工作流模型的输入参数:
(1)N,表示工作流任务的总数量;
(2)α,表示形状参数,即任务总量与宽度(即同一层次上节点的最大数量)的比例,因此,宽度W=int[N/α]。
(3) 工作流类型,提供3种不同类型的工作流:并行工作流、Fork-join工作流和随机工作流。
① 并行工作流:并行工作流中,一组任务形成一个拥有单入口任务和出口任务的任务串,多个任务串形成一个工作流,因此,单个任务的执行仅取决于某个任务,而任务串的串首任务取决于入口任务,出口任务取决于所有串尾任务。并行工作流的层次数为:
层次数=int[(N-2)/W]
(6)
② Fork-join工作流:Fork-join工作流中,任务先分支再连接,因此,只拥有一个入口任务和出口任务,在每个层次上的任务数量取决于任务总数和层次宽度W。Fork-join工作流的层次数为:
层次数=int[N/(W+1)]
(7)
③ 随机工作流:随机工作流中,单个任务与其它任务的依赖性与父任务数量即是工作流DAG中节点的入度,均是随机产生的。此时,任务依赖性和入度定义为:
max indegree(Ti)=int[W/2]
(8)
min indegree(Ti)=1
(9)
Parent(Ti)={Tx|Tx∈[T0,…,Ti-1]},
ifTiis not a root task
(10)
xis a random number and
0≤x≤int[W/2]
(11)
Parent(Ti)={φ},ifTiis a root task
(12)
图2给出以上3种工作流模型的示意图,其中N=10,α=5。仿真中,利用百万指令数MI表示任务长度,兆字节数MB表示任务输出数据量大小。
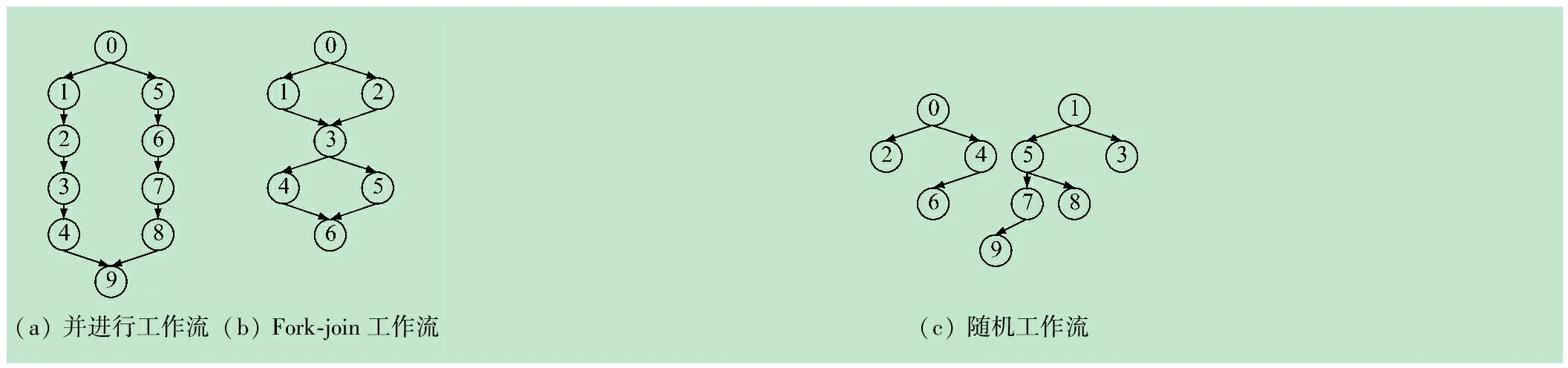
图23种工作流结构
3.2 资源模型
工作流任务的执行环境模拟为异构资源环境,即设置不同处理能力的异构云资源供任务调度。参考文献[10],设置8种不同地域不同能力的云资源,具体参数如表2所示,其中,资源的处理能力以MI/s和Mb/s度量。
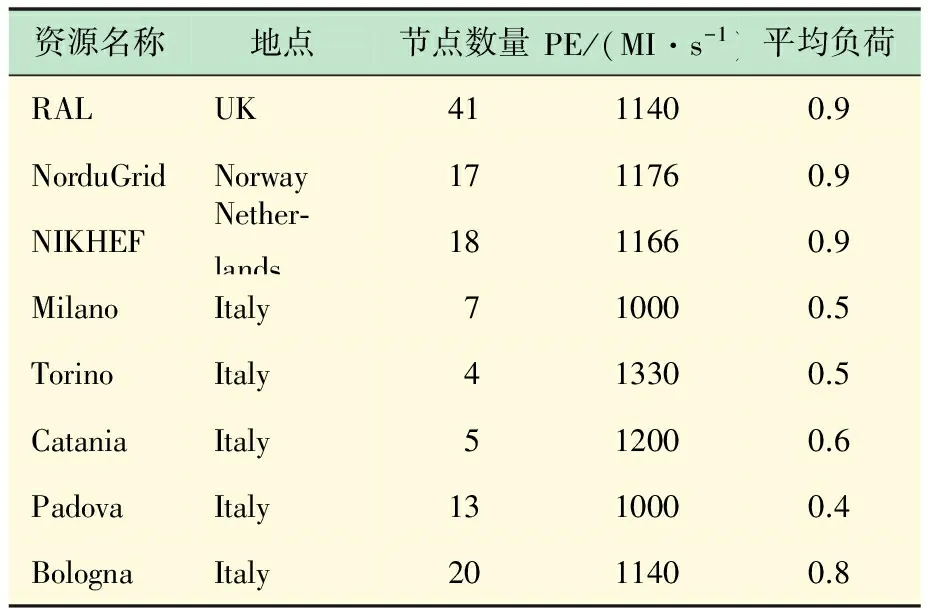
表2 资源配置
3.3 比较算法
(1) Myopic算法[11]:将未映射的任意就绪任务调度至能最早完成时任务的资源上,直到所有任务被调度。
(2) MIN-MIN算法[12]:基于任务在资源上的期望完成时间ECT最小为任务分配优先级,将任务分组并迭代调度,每次迭代中,寻找最小ECTs中使得总时间达到最小的调度方案。
(3) MAX-MIN算法[13]:与MIN-MIN类似,区别在于算法为拥有最长执行时间ECT的任务分配优先级。
(4) HEFT算法[4]:异构最早完成时间算法,给予拥有更高等级的工作流任务更高优先级,该等级使用每个任务的平均执行时间和两个连续任务在资源上的平均通信时间计算得到。
(5) GRASP算法[14]:贪婪随机自适应搜索算法,利用贪婪思想,搜索整个解空间(工作流任务与所有可用资源),将最优解保留至最终解中,搜索过程直到达到最大迭代次数为止。
(6) GA算法[5]:算法利用遗传进化的思想,通过对解空间的快速搜索和对个体的适应度评价,不同于GRASP的随机搜索方式,可以在更短时间内得到较优解。
按算法分类,Myopic、MIN-MIN、MAX-MIN和HEFT均属于启发式算法,而GRASP和GA则属于元启发式算法,以上算法均是分布式计算环境中常用的工作流调度算法。
3.4 实验参数
(1) 工作流类型。并行工作流、Fork-join工作流和随机工作流。通过配置3种不同类型的工作流拓扑结构,可以观察和评估算法在搜索关键路径时与任务结构的关系。
(2)N={50,100,200,300}。通过在工作流中配置不同数量的任务,可以观察算法性能与工作流任务间的关系。
(3)α={10}。该参数值随机选取,由于工作流的结构宽度W=int[N/α],因此该值主要影响拓扑结构中同一层次上的任务最大数量。
为了使实验结果更加具有普遍性,设置每个工作流任务的大小均匀分布于区间[100000MI,500000MI],任务的输出数据量大小均匀分布于区间[1×106,5×106]。同时,对于GRASP算法,调度迭代次数为600次。对于GA算法,参数参考原始配置,如表3所示。
3.5 实验结果分析
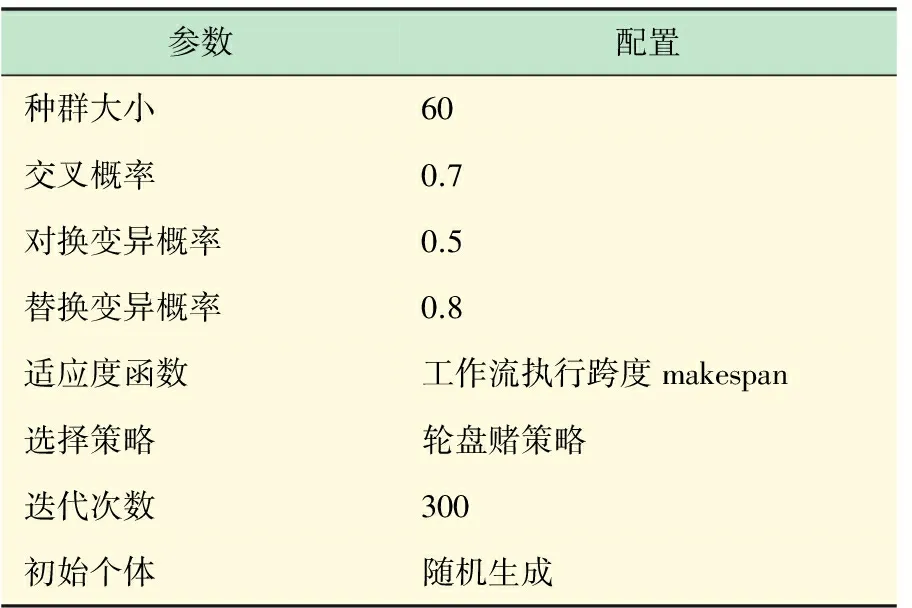
表3 GA参数
为了评估算法在工作流执行跨度上的性能,笔者设计了两种不同的实验场景,第1种场景考虑为静态场景,即:云资源的可用性和负荷保持为静态不变,根据不同的调度算法映射任务至资源并执行调度;第2种场景考虑为现实场景,即:云资源的可用性和负荷为动态改变的,此时,仿真期间每个资源的瞬时负荷(占用PE数量)服从高斯分布。
(1) 静态场景中的执行跨度makespan。图3给出了算法在3种工作流结构中任务数分别为50、100、200和300时的工作流执行跨度。对于随机工作流(图3(c)),CWS-DCP的调度makespan比HEFT低13%左右,而HEFT则优于Myopic、MIN-MIN和MAX-MIN,主要是由于随机工作流中任意任务与出口任务间拥有多条路径,而CWS-DCP通过为任务动态分配优先权可以形成更优的解。由于GRASP和GA搜索了最优解的全部空间,比较CWS-DCP节省了20%~30%的makespan。
对于Fork-join工作流(图3(b)),启发式算法与元启发式算法性能差别较大。任务选择过程中,启发式算法没有考虑映射子任务的影响,因此,所有启发式算法与CWS-DCP拥有类似的结果。然而,在Fork-join工作流中,连接交叉点任务取决于上层所有分支非依赖任务的输出。如果连接点任务分配至与其他资源带宽较低的资源,数据传输时间的增加会影响工作流执行跨度。而元启发式算法GRASP和GA不仅考虑了父分支任务对映射的影响,而且考虑了子分支任务的影响,因此,比较CWS-DCP,性能提升了40%~50%。
对于并行工作流(图3(a)),其执行跨度随着工作流大小的变化表现出相对较慢的指数级增长,原因在于,不同于Fork-join工作流,在调度每一步中,并行工作流中未被映射的就绪任务的数量恒等于W,且只要其父任务完成,该任务即转变成就绪任务。因此,当可用资源量少于未被映射任务量时,任务等待被调度的时间将导致执行跨度的增加。同时,并行工作流中,CWS-DCP和GA的结果优于其他算法,makespan至少低于其他算法20%左右。此时,GRASP的执行跨度高于CWS-DCP,主要是由于任务映射候选解的数量会随着工作流大小的增长呈指数级增加。
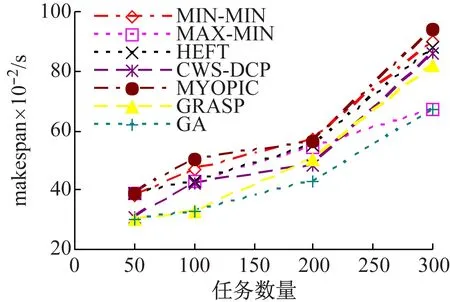
(a) 并行工作流
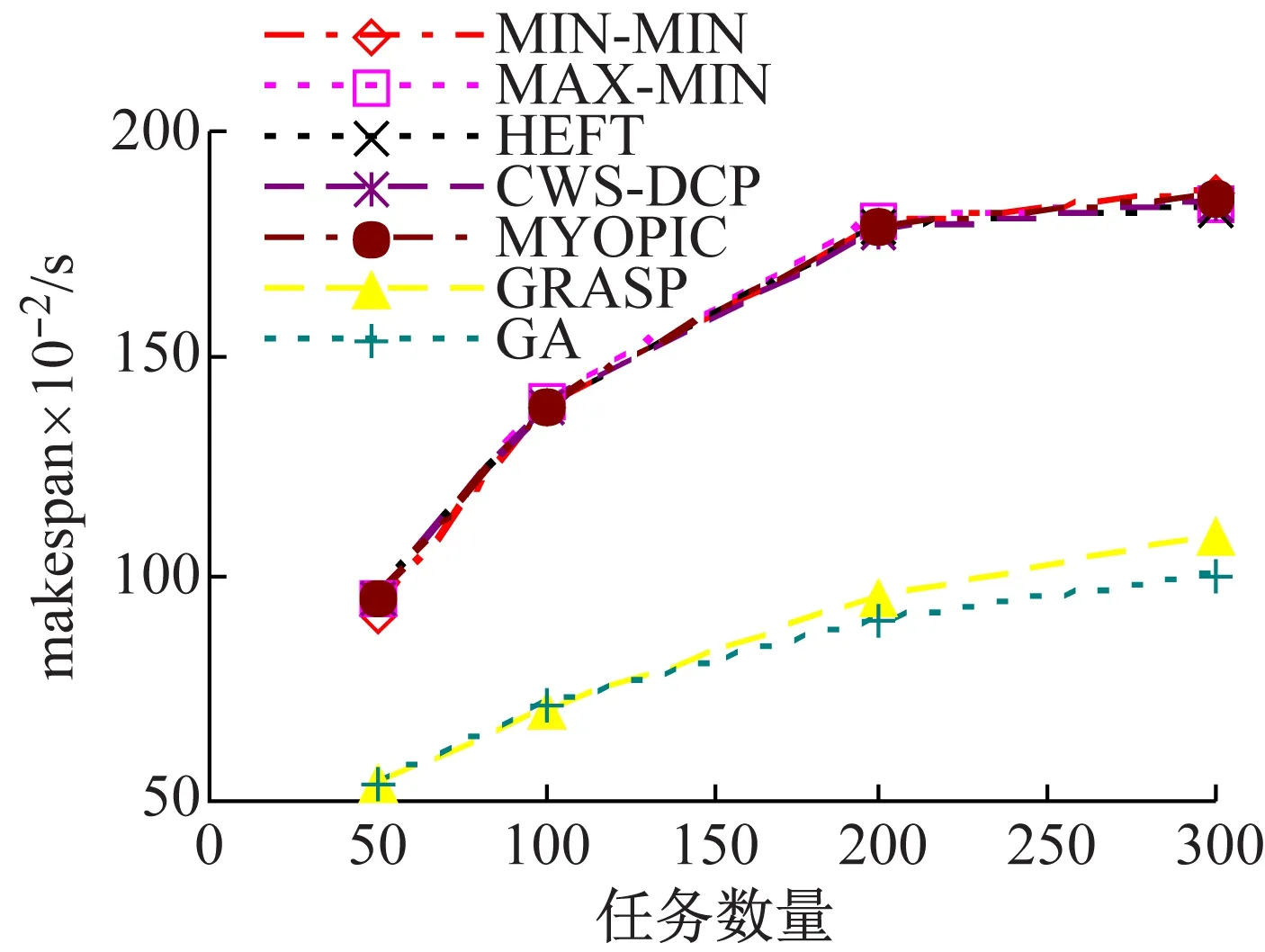
(b) Fork-join工作流
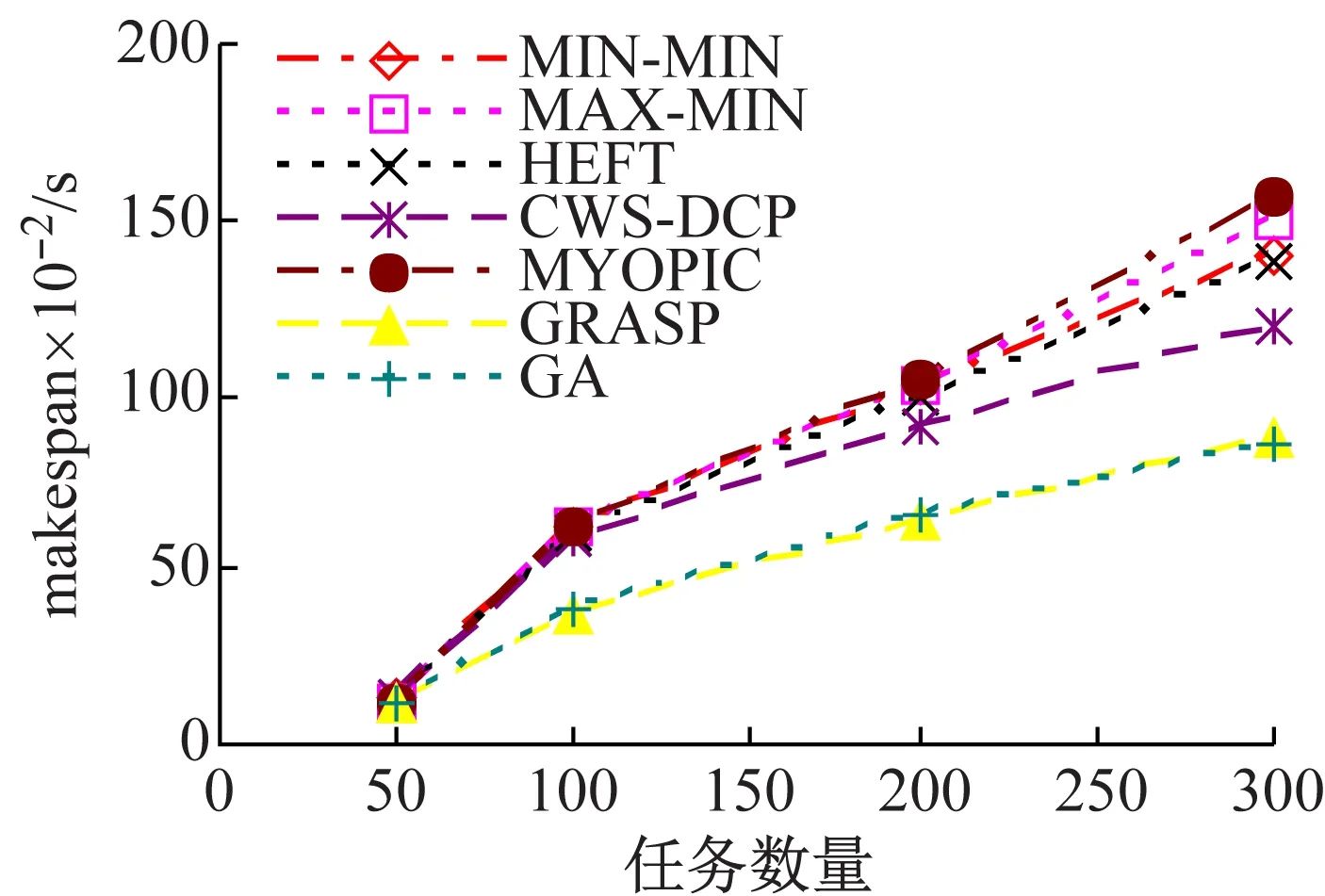
(c) 随机工作流
(2) 动态场景中的执行跨度makespan。由于动态环境中资源可用性是动态变化的,在确定周期中资源可用性信息需要连续不断更新,且任务需要根据资源可用性重新映射。此时,需要比较CWS-DCP与其他启发式调度算法和元启发式调度算法在静态场景下的结果。
图4显示了动态场景下的结果,其资源可用性的更新周期为50 s。此时,资源可用处理元素PE数量和资源上可以开始执行的任务数量会随着资源负荷动态变化。对于GRASP和GA算法而言,如果资源负荷较重且不可用,被映射至该资源的任务需要等待执行,该等待时间会相应影响其他依赖任务的开始时间,并增加工作流执行跨度makespan,GRASP和GA的较差性能也可以反映出这一结果。而且,启发式算法的结果高于元启发式算法30%左右。在所有启发式算法中,CWS-DCP可以比其他算法节省6%左右makespan,主要是由于在CWS-DCP中,在负载较重的资源上等待执行的关键路径上的任务会被重新调度至拥有可用PE的资源上,这会降低关键路径长度,即工作流执行跨度makespan会降低。
同时可以看出,对于相同类型的工作流,动态场景中的启发式算法性能优于静态场景的性能,主要原因是动态场景中的资源负荷和资源可用性是周期性更新的,这表明启发式算法可以更加适应于资源的可用性变化,产生调度方案的更优解。
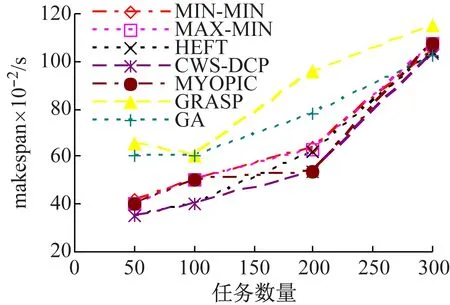
(a) 并行工作流
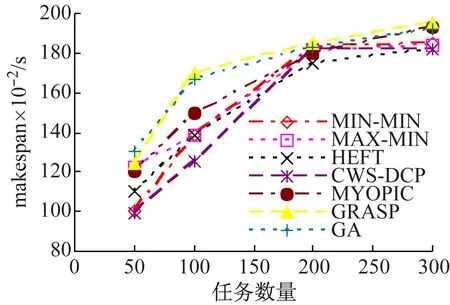
(b) Fork-join工作流
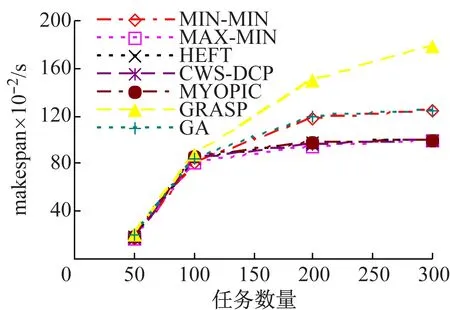
(c) 随机工作流
(3) 算法调度时间比较。图5给出了不同类型工作流下算法的调度时间的比较结果。调度时间即为调度开销,即调度算法产生调度解的运行时间。为了表述的方便,单个任务的平均调度时间(单位:ms)得到的单个调度方案如表4所示,可以看出,为产生一个调度方案,Myopic、MIN-MIN、MAX-MIN和HEFT需要接近1 ms产生调度解,而CWS-DCP需要16~17 ms,且不会随着工作流类型发生变化,主要是由于该算法的任务选择与工作流结构是无关的。

表4 单个任务的平均调度时间 ms

(a) 并行工作流
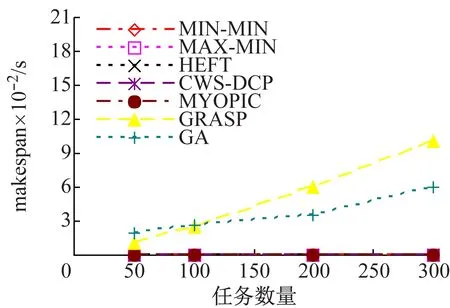
(b) Fork-join工作流
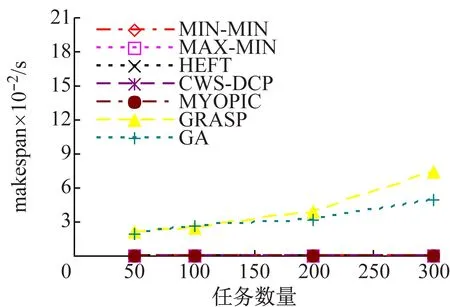
(c) 随机工作流
GRASP的调度时间不仅会随着工作流任务的增加呈指数级增长,而且与工作流结构也密切相关。在每次迭代中,GRASP为每个未被映射的就绪任务建立约束候选资源列表RCL,然后随着为任务选择资源映射。当任务增加时,RCL会呈指数级增长,从而导致调度时间的增加,而RCL本身的大小又依赖于工作流结构的不同。例如:如果工作流由于300个任务组成,并行和Fork-join工作流结构在每个层次包括30个任务,随机工作流结构层次与每个层次上的任务数量均是随机的。因此,在每一步骤中,并行工作流拥有30个就绪任务,Fork-join工作流拥有最多30个就绪任务,随机工作流每个层次上的平均就绪任务数量低于30。因此,随机工作流的调度时间是最低的,并行工作流的调度时间是最高的。
同时,GA的调度时间不会因为工作流类型的变化而变化,由于GA始终执行相同数量的遗传操作,与工作流类型无关。但是,解空间听每个个体的大小等于工作流任务的数量,因此,调度时间会随着工作流大小的增加而增加。
综上,结合图3,很明显在启发式算法中,静态场景中CWS-DCP的性能可以提升20%,尤其对于随机工作流和并行工作流,且与工作流类型无关。在随机工作流和Fork-join工作流,GRASP和GA的性能优于CWS-DCP,但是其调度时间也更高。对于任务数为300的并行工作流,CWS-DCP需要6 s将任务映射至资源,而GRASP和GA分别需要580 s和2 076 s。
在动态场景中,启发式算法可以自适应于资源的动态特征并避免性能降低。但是,元启发式算法在静态场景中且由于确定间隔内映射资源的不可用而表现更差。同时,动态场景中,无论工作流类型和大小的不同,CWS-DCP的性能均优于其他算法。
4 结 语
云资源的动态行为特征导致云工作流调度不同于传统静态分布式计算环境中的调度问题。针对该问题,提出了一种动态自适应工作流调度算法CWS-DCP,算法通过不断迭代计算工作流任务DAG中的关键路径,为关键路径上的任务分配优先级的方式有效实现了工作流任务与云资源间的映射调度。实验结果表明,在资源可用性动态改变的情况下,CWS-DCP算法在多数工作流结构中均能得到更好的调度方案,且与工作流规模无关。进一步的研究将关注多QoS参数下的工作流调度问题,如:考虑任务与服务之间映射时的资源可靠性问题或服务资源执行任务时的能效问题,设计多目标最优化算法实现多QoS指标的同步优化,并以Pareto最优评估多目标优化性能。
参考文献(References):
[1]Liu L, Zhang M, Lin Y, et.al. A survey on workflow management and scheduling in cloud computing[C]//In Cluster, Cloud and Grid Computing, 14th IEEE/ACM International Symposium on. IEEE, 2014:837-846.
[2]Vockler JS, Juve G, Deelman E, et.al. Experiences using cloud computing for a scientific workflow application[C]//In Proceedings of the 2nd international workshop on Scientific cloud computing. ACM, 2011: 15-24.
[3]Cusumano M, Cloud computing and SaaS as new computing platform[J], Communication of the ACM, 2011,53(4):27-29.
[4]Topcuoglu H, Hariri S, Wu MY. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions Parallel Distributed Systems,2012,13(3):260-274.
[5]Huang J. The workflow task scheduling algorithm based on the GA model in the cloud computing environment[J]. Journal of Software. 2014,9(4):873-880.
[6]郑敏,曹健,姚艳.面向价格动态变化的云工作流调度算法[J].计算机集成制造系统,2013,19(8):1849-1858.
[7]Garg R, Singh A K. Multi-objective workflow grid scheduling using ε-fuzzy dominance sort based discrete particle swarm optimization[J]. Journal of Supercomputing, 2014,68(2):709-732.
[8]Wu Z, Liu X, Ni Z,et.al. A market-oriented hierarchical scheduling strategy in cloud workflow systems[J].Journal of supercomputing,2013, 63(1):256-293.
[9]Rodrigo C, Rajiv R, Anton B,etal. CloudSim: a toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms[J]. Software: Practice and Experience, 2011, 41(1): 23-50.
[10]Venugopal S, Buyya R. A Set Coverage-based Mapping Heuristic for Scheduling Distributed Data-Intensive Applications on Global Grids[C]//IEEE/ACM International Conference on Grid Computing. IEEE, 2006:238-245.
[11]Wieczorek M, Prodan R, Fahringer T. Scheduling of scientific workflows in the ASKALON grid enviornment[J]. ACM SIGMOD Record, 2005,34(3):56-62.
[12]Maheswaran M, Ali S, Siegel H J,etal. Dynamic Matching and Scheduling of a Class of Independent Tasks onto Heterogeneous Computing Systems[C]//Heterogeneous Computing Workshop. IEEE Xplore, 1999:30-44.
[13]Mandal A, Auton M. Scheduling strategies for mapping application workflows onto the grid[C]//In Proceedings of the 14thIEEE International Symposium on High Performance Distributed Computing. IEEE,2005:125-134.
[14]Blythe J, Jain S, Deelman E,et.al. Task scheduling strategies for workflow-based applications in grids[C]//In Proceedings of the 5th IEEE International Symposium on Cluster Computing and the Grid. IEEE, 2005:759-767.
[15]杨玉丽, 彭新光, 黄名选,等. 基于离散粒子群优化的云工作流调度[J]. 计算机应用研究, 2014, 31(12):3677-3681.
[16]Calheiros R, Buyya R. Meeting deadlines of scientific workflows in public clouds with tasks replication[J]. IEEE Transactions on Parallel and Distributed Systems, 2014,25(7):1787-1796.
·名人名言·
知识是一座宝库,而实践则是开启宝库的钥匙。
——托马斯·富勒
