设计性实验的基本设计方法

张春华

(沧州师范学院 物理与信息工程学院，河北 沧州 061001)

在理工科教学中为学生开设设计性实验，主要体现出三个方面的教育优势：第一，它是将课堂知识转变为应用能力的有效教学途径；第二，它是有效激发学习兴趣，充分发挥学生潜能的有效教学方法；第三，它是砥砺学习意志，提升科学素养，培养创新能力的有效学习途径.目前在我国全面实施的新课程改革中，不论是在高等教育、中等教育，还是基础教育或职业教育，设计性实验教学伴随着探究式教学理念的不断加强，日益彰显出其有效提高教育教学质量的重要作用[1].然而，如何将传统的、众多的验证性实验改进为设计性实验，是当前人们遇到的一个较为普遍的问题，为此本文通过一系列的实验案例来展示如何进行设计性实验的设计与研究，以供大家参考.

1　设计性实验的基本设计方法

一般来说，在学生掌握一定的专业基础理论和一定的基本实验技能之后就可以开设设计性实验，进行设计性实验的教学设计要注意以下几个方面.

第一，设计性实验的引入要引人入胜、发人深省.任何一个实验问题，哪怕再简单，只要经过一个适当的教学设计都可以促使学生产生较为强烈的求知欲.一般来说，提升实验的吸引力应注意两点：第一点，用好奇打动人，比如密度测量实验的研究对象可选定新颖或新奇的客观存在，切忌庸俗无味；第二点，用实际应用价值或探索意义感染人，比如注重实验的社会应用性与理论探索的前瞻性，切忌脱离实际与理论发展，仍以最为普通的密度测量实验研究为例，其研究对象与探索方法的选定还应紧密联系其实验的社会科技与发展意义(比如物质鉴别、环境监测)以及未来理论的进一步构建与发展意义(比如，从宇观到宏观到微观，从实物到场物到探索中的暗物质与暗能量)等等.

第二，设计性实验的研究要立意科学、探究准确.首先，就任何一个设计性实验而言，要有一定的实验精度作保障，否则，它的实验研究是不可信的.如何保证一个实验的研究精度呢？从实验测量来讲，这就需要紧扣测量精度的定义与正确运用误差传递公式来做具体设计与分析.比如，用量筒和天平测某一可溶于水的固体的密度，要求测量精度不低于5%，如何进行实验设计？对于这样一类间接测量问题，我们通常用四步设计法即可完成.

第一步，将“测量精度不低于5%”这一要求，用测量精度的定义转换成数学表达式

Δρ/ρ≤5%

(1)

第二步，运用误差传递公式Δρ/ρ=ΔV/V+Δm/m将数学表达式(1)式进一步细化为

Δρ/ρ=ΔV/V+Δm/m≤5%

(2)

第三步，将测量精度要求合理分配给细化的表达式——不等式(2)式的左端的每一部分(亦即分配至每一个测量量)，比如，做等精度分配时，有

ΔV/V≤2.5%，Δm/m≤2.5%

(3)

第四步，根据精度分配结果(3)式，选定满足精度要求的仪器设备与相关实验方法.

由于V=V2-V1,ΔV=ΔV2+ΔV1=uV,Δm=um(V1与V2分别表示待测固体放入量筒前与完全浸没于量筒水中以后的量筒读数，uV和um分别表示量筒与天平的最小分度值)，带入(3)式即可得出选择量筒与天平的标准为：

V≥40uV,m≥40um

(4)

假如选取最小分度值uV=1ml的量筒与最小分度值um=0.02g的天平，带入(4)式可知，

V≥40ml,m≥0.8g

(5)

亦即，此时所选取的待测物的体积与质量必须满足(5)式，才能满足测量精度要求.

第三，设计性实验的探索要具有充裕的自主提升空间.设计性实验的最大优势之一，就是能够设法调动并有效发挥学生的潜能，这是由于实验前就进行了充分的设计与思考.比如，在上述测固体密度的实验设计过程中，有两方面的设计考虑可提高实验测量的精度.首先，是关于测量体积前加入量筒的水位是否与量筒的某一刻线对齐的思考问题.它可以显著影响测量结果的精度.当事先令V1与量筒的某一刻线对齐时，由于ΔV1≈0，将使ΔV=ΔV2+ΔV1≈ΔV2≤uV/2；否则，由于ΔV1≤uV/2，ΔV2≤uV/2，致使ΔV=ΔV2+ΔV1≤uV，测量精度大大降低.其次，关于思考待测物体积V的大小对提高测量精度的影响问题.由于量筒与测量方法一定时，ΔV一定，故V越大，ΔV/V越小，因此体积V的测量精度越高，这样在量筒测量范围内，待测物尽可能选的体积要大一些.同理，对待测物质量m的选取也是如此，当天平一定时，Δm=um一定，故待测物质量m越大，质量的测量精度Δm/m越高.因此，如果这些方面的设计与思考运用到位，将非常有利于培养学生的研究能力.

第四，设计性实验的内容要具有应用性与前瞻性.选定设计性实验的题目时，人们常常感到无从下手，其实任何一个实验都可以做设计性改进.大学本科生阶段的设计性实验要立足于基础性与创造性、典型性与前瞻性、应用性与地方性、科学性与思想性相结合的原则，把握住这些要点就可以在实验的设计性研究中做到纵横驰骋、游刃有余.比如，做密度测量实验的设计性改进时，它的应用性、科学性与创造性主要表现之一，就在于深入分析与探究将密度测量精度要求如何分配到各个直接测量量方面.仔细分析一下，可以发现做上述等精度分配时，(3)式确立的选择测量器材的标准(4)式或(5)式欠应用性与科学性，主要表现在选择量筒的标准过于苛刻(要求的待测物的体积偏大，这与现存的同量级的量筒的最小分度值难以匹配)，而选择天平的标准又过于宽松，为此做创造性改进时，应将测量精度要求的等精度分配方法变为科学的非等精度分配方法，进一步说，应该使待测量体积V分得的部分尽可能得多，而待测量质量m分得的部分尽可能得少，比如有ΔV/V≤4.9%，Δm/m≤0.1%，如此等等.与此同时，选题应与地方、生活或科研等实际需求密切相连，诸如与地方空气质量的监测等直接挂钩；做测重力加速度实验的设计性改进时，与地方的重力加速度、地方的经纬度、海拔高度、地球自转等精确测量相联系，加强地方性，加强科研性，加强应用性等等.

2　设计性实验的案例举例

2.1　探索未知形变规律的设计性实验

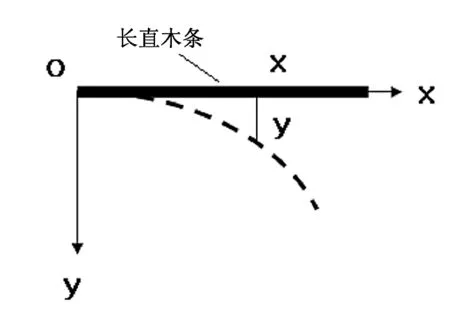
图1　长直木条形变示意图

引领学生掌握探索未知规律的基本方法，对提高学生的研究能力与探索能力非常重要.下面以探索小长木条的未知形变规律实验研究为例，从理论设计方面做一分析.

2.1.1设计性实验题目

探索一根长为l且一端被固定并呈现水平悬置状态的小直木条(或小铁条)在竖直向下的恒定外力作用下的形变规律(参见图1).

2.1.2实验培养目标

第一，提高学生在初步观察与思考之下建立规律模型的能力；第二，提高学生有效运用实验手段的能力；第三，提高学生有效获取和处理实验数据及误差分析的能力；第四，提高学生形成科学结论的能力；第五，提高学生深刻反思与深入探索的能力.

2.1.3实验方法分析

用实验探索未知规律，首先要对探索的未知规律从理论上建立某种合适的探索模型，然后通过一系列的实验观测和数据分析及处理后，再经过不断改进与完善研究后才可以确定.

(1)以基本认识为基础，建立理论探索模型

以长木条的固定点为原点O、长直木条的水平方向为x轴、竖直向下方向为y轴，建立x-y直角坐标系.为寻找形变规律，在长直木条的不同x位置，悬挂同一重物W，并假设长直木条的形变规律为y=f(x)，这里y表示长直木条在x位置处沿y轴方向发生的形变量(见图1).

通过实验观察可发现，x增加，y也增加，而且有：x→0，y→0；x→最大，y→最大且似乎带有某种幂指数的属性，因此可将y=f(x)的具体数学模型建立为如下形式：

y=axb

(6)

式中a和b为待定系数.

(2)选用科学的数据处理和误差分析方法确定待定系数a和b

对于(6)式所示的规律模型，需要选用线性拟合法或最小二乘法来进一步确定待定系数a和b.

将(6)式两边同时取自然对数得

lny=lna+blnx

(7)

这表明，当以lnx为新的自变量X，以lny为新的因变量Y，在X─Y坐标系中做lnx─lny图时，由(7)式做得的图线应该为一条直线，而且b和lna分别为该直线的斜率和截距.这样只要在实验中获取测量列数据(xi，yi)(i=1，2，3，……，n)进而取得测量列数据(lnxi，lnyi)时，就可以在X─Y坐标系中做得lnx─lny直线，从而进一步确定出待定系数a和b.

2.1.4具体实验探究

第一，做实验获取数据.表1展示了便于数据记录与数据处理的基本表格设计方式，也记录了我们的一次测量结果.

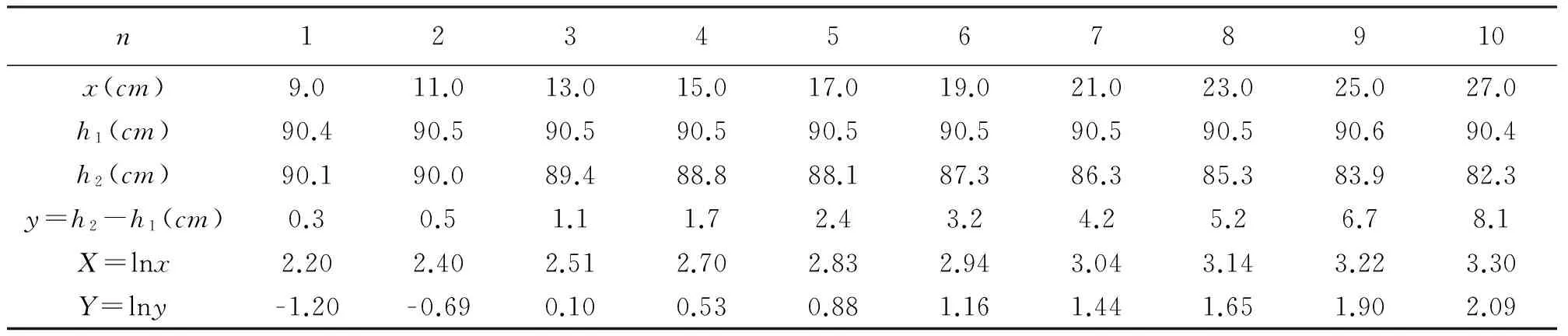
表1　测量数据

第二，在X-Y坐标系中做lnx─lny图(图2)，验证规律模型的科学性.

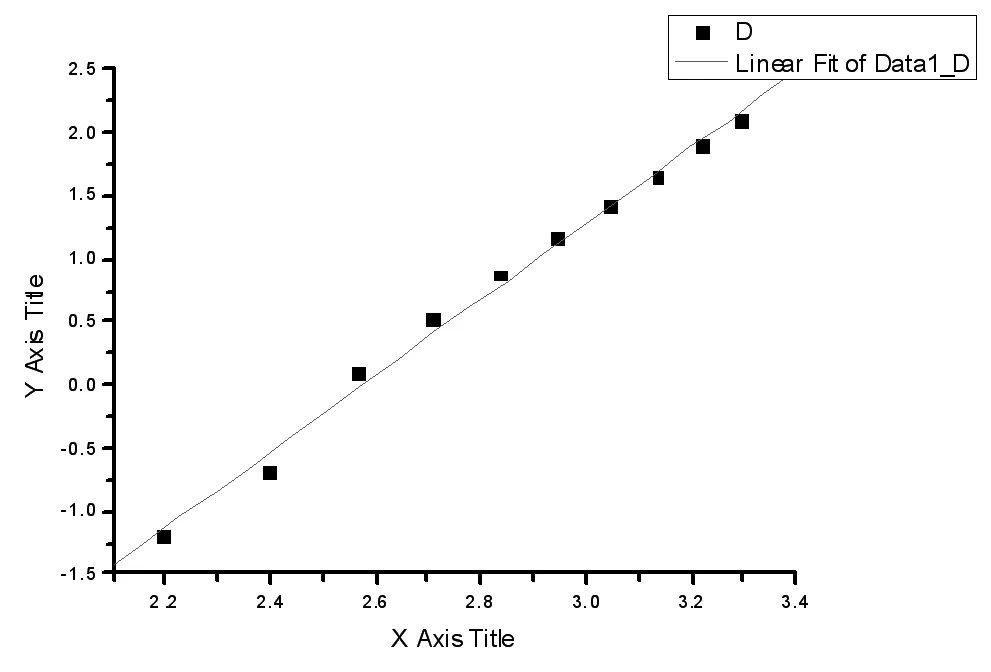
图2　lnx-lny函数图(originPro7.5软件拟合图)

根据表2做lny=lna+blnx拟合，得图2和表2所示拟合结果.

表2　双对数规律lny=lna+blnx的originPro7.5拟合结果

如此，我们探索得到的形变规律为

y=axb=(4.2133×10-4)x3.01921=(4.2×10-4)x3.019

表2清晰表明，这一形变规律比较符合实际情况，其拟合相似概率近似为99.6%.

2.1.5创新性探索

(1)规律建模深入探索

在建立探索该未知规律的理论模型时，选择了(6)式的形式，其实根据其形变的基本形状，比如似乎具有某种抛物线形状，或类似某种局部的正弦函数形式等，因此也可以考虑选择建立抛物线规律拟合y=a+bx+cx2+…或局部正弦函数规律拟合y=asinb[xπ/(2l)](0≤x≤l)等.

图3和表3是基于实验数据表1所得的抛物线拟合结果.

图3　抛物线规律y=a+bx+cx2的originPro7.5拟合图

拟合量拟合值误差待定参数a0.643180.28555待定参数b0.195760.03389待定参数c0.017429.32245E4线性相关系数拟合值标准偏差R0.99920.08569

从表3可以看出，抛物线规律y=a+bx+cx2的拟合相似概率近似为99.9%，大于双对数规律lny=lna+blnx的拟合相似概率99.6%，因此就寻找形变规律而言，抛物线规律较前者更为合理，但作为实验探究能力培养而言，抛物线规律稍显复杂，因此选择前者就较为合适了.

通过深入探究，尝试不同规律模型的拟合与分析，可进一步锻炼与提高探索未知规律的基本能力，培养与提高创造性思维.

(2)凸显应用性的建模方法

可将这一探索未知规律的方法灵活应用于解决实际问题.比如，探索汽车通过桥梁时桥梁的形变规律，由此可以建立基于“抛物线”的初步规律模型

y=a(l/2-x)b(-l/2≤x≤l/2)

也可以建立基于“余弦曲线”的初步规律模型

y=acosb(πx/l)(-l/2≤x≤l/2)

这里已假设桥梁长为l，并以桥梁的1/2处为原点建立坐标系.

2.2　精确测量物理量的设计性实验

案例一主要介绍了如何进行探索未知规律方面的设计性实验的设计方法，下面通过对给出测量精度要求的测薄凸透镜焦距的实验设计，看一看如何进行测量物理量方面的设计性实验的设计.

2.2.1设计性实验题目

主要利用光具座仪器设计一个测量薄凸透镜焦距的设计性实验，要求测量精度不低于5%.

2.2.2实验设计思路

第一，明确测量精度要求

Δf/f≤5%

(8)

第二，明确测量原理与误差传递情况

(1)测量原理式

1/f=1/u+1/v

(9)

(2)误差传递公式

(10)

(3)根据误差传递公式将测量精度要求细化：将(10)式带入(8)式得

(11)

第三，采用简洁实用的特殊情况深入实验设计.常采用特殊情况思考法将复杂设计情况简洁与实用化.比如，考虑u=v=2f的特殊情况.此时，原理式简化为

u=v=2f

(12)

因此，误差传递公式也简化为

Δu=Δv=2Δf

(13)

这时，将(12)(13)式带入(11)得

f≥10Δu=10Δv

(14)

由此可以得出一个满足5%的测量精度要求的实验设计方案为：

第一，可采用u=v=2f的测量方法；

第二，所选待测透镜的焦距满足条件f≥10Δu=10Δv.

当然，也可以利用原理式(9)，讨论f=u,u/2,u/4等情况的实验设计问题，以供进一步地比较选择.

2.2.3测量方法深入讨论

一般情况下Δu或Δv的测量方法有下述三种情况：

第一种，成倒立放大实像时，动“物”定“屏”：移动成像物，固定成像屏幕，在屏幕上呈现出清晰的像.此时确定出的能成出清晰像的成像物的最佳移动范围的一半既为Δu(因为此时若定“物”动“屏”，将使确定出的能成出清晰像的“屏”的最佳移动范围更大，从而使确定的Δv大于前者确定的Δu，使测量精度变低).

第二种，成倒立缩小实像时，定“物”动“屏”：移动成像屏幕，固定成像物，在屏幕上呈现出清晰的像.此时确定出的能成出清晰像的屏的最佳移动范围的一半既为Δv(因为此时若定“屏”动“物”，将使确定出的能成出清晰像的成像物的最佳移动范围更大，使测量精度变低).

第三种，不论成像属于放大、缩小或相等的哪一种情况，都可以将“物”与“屏”固定在两者相距不小于4f的位置，而仅仅移动凸透镜，使之在屏幕上呈现出清晰的像.此时，确定出能成出清晰像的“镜”的最佳移动范围的一半，既为Δu=Δv.此时，由于“物”与“屏”固定，“物”与“屏”两位置的确定将不产生“景深”方面的误差，这样操作更为便捷.

因此，一般来讲，第三种方法是人们经常使用的方法.

2.3　由实验器材科学制定实验方案

进行实验设计，通常采用两种思路：第一种，从测量精度要求出发，确立实验方法和选定实验器材，这也是人们常用的方法(如上述案例一)；第二种，从现有实验器材出发，根据测量精度要求，科学制定实验方案.下面，以伏安法测电阻实验为例，说明如何运用第二种思路来设计实验.

2.3.1设计性实验题目

使用J0407型安培表与J0408型伏特表设计一个伏安法测电阻实验.

2.3.2实验设计思路

从两表出发进行设计.

2.3.3实验设计方案

第一，按照省电原则选定两表量程.按照省电原则，两表均选取小量程：J0407型安培表——选0.6A量程；J0408型伏特表——选3V量程.

第二，根据两表精度级别与最佳测量范围确定实验精度.对于电压表与电流表来说，最大测量不确定度与最佳测量范围分别为

ΔU=Umaxav%,ΔI=ImaxaA%

这里，Umax和Imax分别表示伏特表与安培表的满偏量程，aV和aA分别表示伏特表与安培表的精度级别.因此由两表确定的测量电阻的精度为

亦即，有

(15)

使用J0407型安培表与J0408型伏特表时，Umax=3V，Imax=0.6A，aV=2.5,aA=2.5,由此，(15)式给出使用J0407型安培表与J0408型伏特表测电阻时的测量精度为

(16)

第三，从两表出发选定最佳待测电阻.考虑到测量时，两表需同时进入最佳测量范围才使测量数据质量最好，因此待测电阻的最佳阻值需选定为：

(17)

又考虑测量时最大电流可达0.6A(安培表的满偏量程)，因此待测电阻的最大允许工作电流IR不应低于0.6A.这样，从两表出发选定最佳待测电阻为：

R=5Ω，IR≥0.6A

(18)

第四，进一步选定测量方法.首先，考虑采用内接法.若忽略理论误差，根据微小误差准则要求[2][3][4]

R≥20RA/(7.5%)=20×0.125/(7.5%)≈33.3(Ω)

(19)

显然(19)式与(17)式的要求相差甚远，故使用内接法不合适.

然后，考虑使用外接法.此时，若忽略理论误差，根据微小误差准则要求

R≤RV7.5%/(20-7.5%)=3000×7.5%/(20-7.5%)≈11.3(Ω)

(20)

很明显，(20)式能够满足(17)式的要求，因此使用外接法测电阻方法科学合理.

第五，在具体测量的操作方面，为了有力消除两表指针轴摩擦带来的误差，选用导号法，并以安培表(或伏特表)为测量标准表；在数据处理方面，应采用作图法，并辅之以最小二乘法加以深入讨论(比如采用oringin等软件).

综上所述，选定的最佳实验设计方案为：(1)两表均选取小量程；(2)待测电阻选取R=5Ω,IR≥0.6A；(3)使用外接法来测量；(4)采用导号法来进一步获取数据与采用作图法测量数据等.需要注意的事项是，测量时两表须同时进入最佳测量范围时再获取数据.

3　结论

本文给出了进行实验设计的基本思路与基本方法.综上所述，一般情况下有两种设计与研究思路：第一种，从测量目的与测量精度要求出发，确立实验方法与选定实验器材，这也是人们进行理论设计的常用方法；第二种，从现有实验器材出发，根据测量任务与测量精度要求，科学制定实验方案，这也是人们就地取材、挖潜创新的基本方法.总体来讲，进行设计性实验教学设计要力争满足五个方面的基本要求：实验题目的融洽性(内容贴切，意义明确)，实验方法的科学性(原理简洁，科学规范)，实验测量的技能性(保证精度，体现技巧)，实验研究的深入性(思维宽阔，运用深厚)，实验探索的魅力性(引人入胜，启迪创新).只有这样，才能从理论上把握设计性实验的本质，在实践中充分发挥其能力培养、素质提高的重要作用.

参考文献：

[1]张春华.如何正确理解与有效实施探究式教学[J].物理教学探讨，2011，29(1)：1-3.

[2]张春华.消除伏安法测电阻理论误差的实验设计标准——微小误差理论在实验设计中的应用举例[J].物理实验，1995，15(2)：71-72.

[3]Chunhua Zhang.The Criterion for Expressing Errors with Significant Digit[J].Applied Mechanics and Materials，2012，143-144：815-818.

[4]Chunhua Zhang.Best Method of Measuring Resistance with Voltammetry[A].Samson Yu.Proceedings of the 2014 International Conference on Electrical，Control and Automation[C].Lancaster，Pennsylvania(U.S.):DEStech Publications，Inc.，2014.