基于车轮减震机构设计与分析
2018-04-11张志平张西培李虎
张志平,张西培,李虎
前言
21世纪以来中国经济发展迅猛前沿科技层出不穷,人民生活水平急速提升生活质量和要求也在不断升高,汽车已经成为每家每户的必备品不再是奢侈品,然而随着汽车的使用在增加环境污染问题和交通问题变得尤为突出。
在大城市的快节奏下人们每天生活在车水马龙的环境中,每日上班面对的是排成长龙堵车现象,假日旅游或闲暇外出游玩都为出行大大发愁,自驾游俨然成为一种年轻人最热爱的方式但由于车辆较多也无法很欢快的旅行。
1 车轮减震机构创新点及其未来发展前景
车轮在材料选择上选择了强度大重量轻的铝合金型材,在承受相同载荷的条件下铝合金的性能具有较大的优越性,同时使用铝合金加工车圈可以节省成本,加工便捷。
将花鼓轴通过弹簧阻尼器与轮圈进行连接达到在运行时承受的载荷作用于弹簧阻尼器上,直接通过减震器减震后再输送到车架上,这在传递冲击的过行程中极大的降低了载荷大小,减震效果相显著。
由于车轮是将弹簧阻尼器通过等角度排列,将花鼓轴承受的载荷平均分布在三个液压轴上,与传统的将载荷作用在两个减震器上,极大的减小了单个减震器承受的载荷冲击,大大提高了减震器的减震效果。使驾驶舒适度得到显著提升。
2 结构设计及受力分析计算

图2 .1

图3 .1
轮圈轮毂采用铝合金型材制作结构为图1所示,为减小单个弹簧阻尼器上所承受的载荷,将轮圈与轮毂按照θ=120°间隔进行排布,使得单个弹簧阻尼器承受的载荷最小。其大小长度将轮圈的尺寸定为。常用型26英寸,弹簧阻尼器通过定制确定其中心距为270 mm总长为310 mm。由于轮圈和弹簧阻尼器的尺寸已确定,对花鼓轴上的减震器连接块和轮圈上的减震器连接块的尺寸进行确定。
由花鼓轴的内部直径为40 mm可知花鼓轴外径距离轮圈内径的距离为310 mm,由于弹簧阻尼器的总长度为310 mm所以连接块不能直接垂直于轮圈和花鼓轴,且若将弹簧阻尼器安装为垂直于轮圈和花鼓轴将产生较大的弯矩对连接块的剪应力影响较大容易使连接块产生断裂的危险。因此要将花鼓轴的连接块与轮圈的连接块错开角度,将其分开α=45°连接,这样极大的增加了连接块的抗弯曲应力又增加了安装空间可以容纳弹簧阻尼器的尺寸。
通过花鼓轴连接块与轮圈连接块相差α=45°可计算出连接轴的大小,通过权衡受力的分布状态取轮圈连接轴的高度为45 mm,孔径10 mm,花鼓轴连接块高度为40 mm,孔径10 mm。确定安装尺寸,将弹簧阻尼器的有效行程L与连接块尺寸相结合,检验当花鼓轴承受载荷使得弹簧阻尼器发生行程改变位置变化时,弹簧阻尼器的轴是否会与花鼓轴外径发生干涉碰撞,并通过理论推导得出承受较大冲击减震器发生极限行程运动时是否产生干涉,且通过自由度计算公式
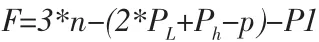
n——为活动构件数
PL——为低副数
Ph——为高副数
P——为虚约束
P1——为局部自由度
其中n=8,PL=10,Ph=1,P=0,P1=0;代入求得F=3>1
所以该机构没有固定的运动轨迹,轮毂可在X、Y、Z轴上进行相对移动。因为当行驶时自行车车轮是转动的花鼓轴上的载荷也在变化,作用于单个弹簧阻尼器上的力大小方向各不相同。但花鼓轴运动的平面是固定的因此不会出现轮毂侧向运动,保证了车轮平稳转动的要求。

图4 .1

图4 .2
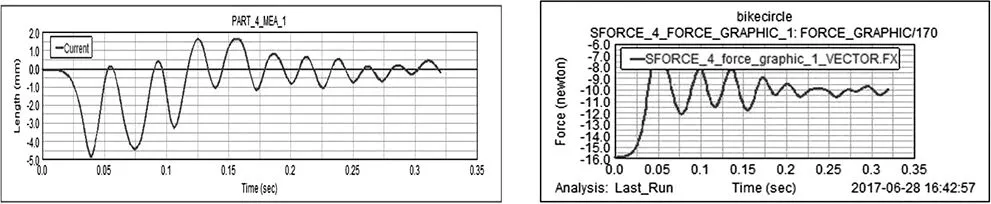
图4 .3
3 车承受自身质量时受力分析
由结构尺寸可得到计算所需的长度大小,当只承受车辆自身重力时,将花鼓轴承受的力进行放大,使得车辆自身重力全部作用在花鼓轴上即G=25kg,由花鼓轴连接块与弹簧阻尼器的连接方式得:
其中F1、F2、F3之间角度为θ=120°,所以
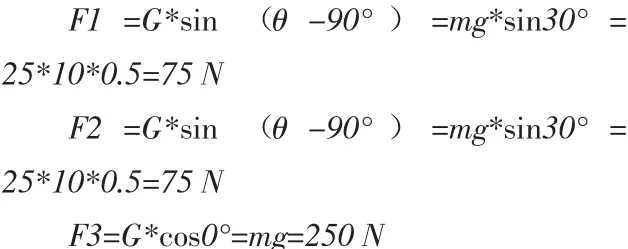
通过求得F1、F2、F3的值可求其他分力
已知花鼓轴连接块与轮圈连接块之间的夹角α=45°
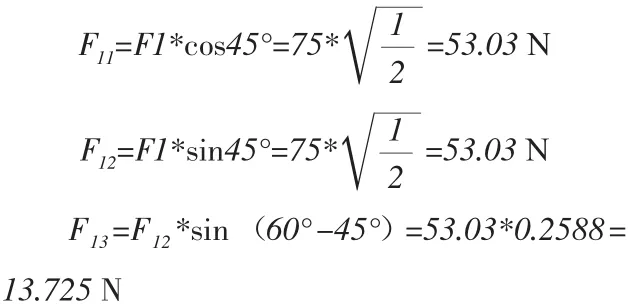
由计算出的各分力,找出作用在销轴上的力为F1,F2,F3
对销轴进行应力计算

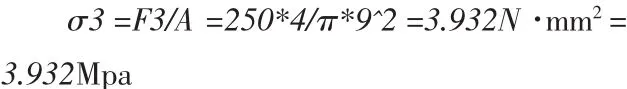
对连接块进行最大正应力计算
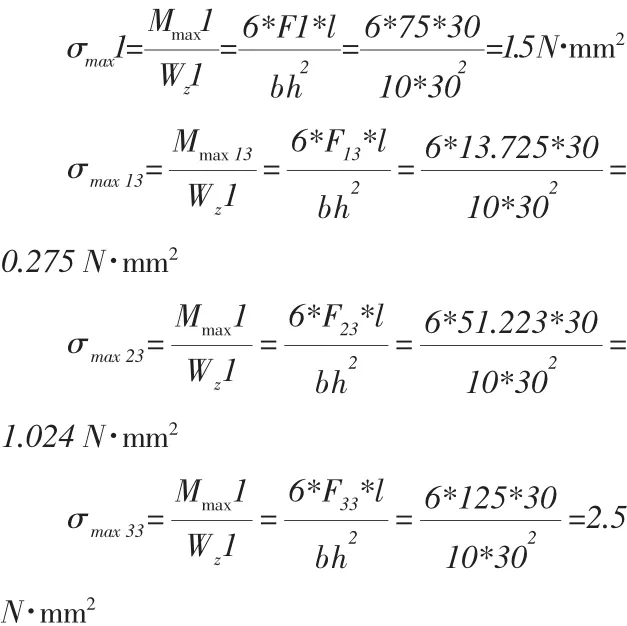
销轴的材质选择为碳素钢Q235,其许用应力σmax=235 Mpa,计算得出最大正应力小于其许用应力,故安全结构符合要求。
由上述计算分析可得,在车辆行驶时受力分析情况相同受力大小不同,因此将上述计算中的G更换为G+G'=F
由许用应力反向求F极限冲击力
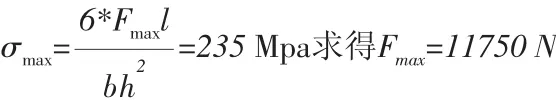
故该机构能够承受最大冲击力为11750 N。
4 ADAMS动力学仿真分析
通过对车轮受力分析,得出各个连接处的受力状态及其大小,根据其具体的数据在ADAMS中进行数据建模,将同等尺寸的车轮结构通过ADAMS中的模块构建出分析模型(如图4.1),根据其受力对其进行受力加载,并运行得出其轮毂在受外力冲击时振荡时间与轮毂位移(如图4.2)、时间与轮毂受力(如图4.3)的关系。
5 结语
通过ADAMS动态分析得出自行车减震机构轮毂处位移、速度、受力等数据随时间的变化曲线,当轮毂承受一定载荷时,轮毂的位移会随着载荷的变化而相应产生变化以应对变化载荷带来的时变冲击。从曲线图可以看出在较短的时间内自行车减震机构可以快速反应消除冲击带来的较大位移偏差,从而实现较好的减震效率。
减震力与时间的关系图可以看出,在减震机构消除冲击的较短时间内,减震力的变化幅度相对较小,得出在减震工作的过程中不会对车轮造成较大的冲击震荡,减震过程较为轻缓,符合减震器的减震舒适需求。
参考文献:
[1]王永涛,李成,马志垒基于ADAMS/Car Ride汽车平顺性仿真[J]..机械设计与制造.2010.
[2]刘进伟,吴志新,徐达.基于ADAMS/CAR 的某轿车悬架优化设计[J].轻型汽车技术.2006.
[3]Nielens H,Lejeune T M.Energy cost of riding bicycles with shock absorption systems on a flat surface.[J].International Journal of Sports Medicine,2001.
[4]Nielens Henri,Lejeune Thierry.Bicycle shock absorption systems and energy expended by the cyclist.[J].Sports Medicine,2004.
[5]Chia-Pei Chou,Wan-JuLee,Ai-ChinChen,Ren-ZuoWang,I-ChunTseng,Cheng-Chun Lee.Simulation of Bicycle-Riding Smoothness by Bicycle Motion Analysis Model[J].Journal of Transportation Engineering,2015.
[6]周志才,吴新跃,张文群,谢最伟.基于弹簧阻尼模型的碰撞动力学研究 [J].湖北工业大学学报,2012.
[7]严蔚,刘承斌,王柏生,钱国桢.新型高阻尼弹簧及其性能研究[J].振动与冲击,2004.
[8]刘增华,李芾,傅茂海,卜继玲.空气弹簧的刚度及阻尼特性研究[J].机车电传动,2005.
[9]李松焱,闵永军,王良模,安丽华.轮胎动力学模型的建立与仿真分析[J].南京工程学院学报(自然科学版),2009.
[10]阮大文.动力学分析法概论[J].分析试验室,1986.
