基于动态贝叶斯网络的突发事件情景推演模型研究

2018-04-11巩前胜

西安石油大学学报（自然科学版） 2018年2期

巩前胜

(1.西安科技大学安全管理研究所，陕西西安 710054; 2.西安石油大学经济管理学院，陕西西安 710065)

巩前胜.基于动态贝叶斯网络的突发事件情景推演模型研究[J].西安石油大学学报(自然科学版),2018,33(2):119-126.GONG Qiansheng.Research onscenario deduction model of emergencybased on dynamic Bayesian networks[J].Journal of Xi'an Shiyou University (Natural Science Edition),2018,33(2):119-126.

引言

目前，国内外针对突发事件“情景-应对”模式的研究几乎涉及到“情景-应对”决策流程的各个环节，包括情景概念[1-4]、情景描述与要素提取[5-7]、情景演化[8-10]、情景表达[11-13]、情景网络构建与情景推演[14-16]等。由于突发事件具有动态性、不确定性、演进规律与路径复杂等特点，如何根据目前的情景状态推演突发事件的未来发展趋势，以便提前做出应对，应是研究关注的重点。然而，现有文献关于情景推演的研究，大部分还停留在定性描述阶段，较少涉及数据支撑的定量模型，因此在突发事件情景推演的精确度以及效率方面还有欠缺。本文抓住突发事件情景演变“动态性”的特点，分析突发事件的情景动态演变规律与路径，提出了基于动态贝叶斯网络的情景推演模型。

1　突发事件情景演化规律与路径分析

1.1　情景演化规律

突发事件情景演化是一个动态的过程，包括情景构成要素以及要素之间的相互关系。突发事件情景构成要素主要包括以下4个方面：(1)情景状态，用字母S来表示，主要指应急客体的状态，包括致灾体情景状态以及承灾体情景状态；(2)应急活动，用字母B来表示，是指应急主体为了改变情景状态对

应急客体采取的处置行为与措施；(3)外部环境，用字母H来表示；(4)应急资源，用字母M来表示，属于应急活动的外部约束条件。这4个构成要素之间相互作用构成一个基本单元，如图1所示。

图1　突发事件情景演化基本单元Fig.1　Basic units of emergency scenario evolution

在图1中，S表示当前情景状态，在外部环境H的影响下，以及应急主体的应急活动B干预下，在应急资源M的约束下，情景状态发生变化，进入下一情景状态S1，从情景状态S到S1的转换，实现一次完整的情景演化过程，称之为突发事件情景演化的一个基本单元。

假设一个突发事件从发生到消失共经历n次情景转化，情景状态分别记为S0，S1，S2，…，Sn-1，Sn，其中S0为初始情景状态，Sn为消失情景状态，每个情景状态所在的时刻分别为t0，t1，t2，…，tn-1，tn。Bi，Hi，Mi分别表示ti时刻的应急活动、应急环境以及应急资源约束，i∈(1,2，…，n)。突发事件情景演化如图2所示。

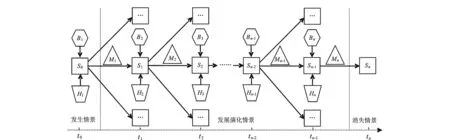
图2　突发事件情景演化规律Fig.2　Emergency scenario evolution rule

在图2中，S0为突发事件的初始情景状态，发生时刻为t0，在应急活动B1的干预下、应急环境H1的影响下、应急资源M1的约束下，情景状态发生变化，进入下一个情景状态。由于应急环境和应急资源约束不同，以及采取的应急处置措施不同，使得情景演化具有不可预测性，因此，下一个情景状态也就具有多种可能性。假设到达时刻t1，情景状态确定为S1，在B2的干预下以及H2和M2的影响下，情景状态又发生演化，出现新的情景状态；以此类推，直到时刻tn，情景消失，整个应急处置过程结束，情景演化过程终止。

1.2　情景演化路径

由于突发事件情景演化是一个连续的过程，因此，应急处置也就是一个持续的过程。应急决策主体根据即时情景状态，做出应急决策并采取措施，从而改变当前的情景状态，进入下一个情景状态。在对下一个情景状态做出应急决策之前，一般会对上一次的应急效果做出评估，其结果一般分为2种：达到预期或未达预期。达到预期表示应急决策起到应有的效果，事态已被控制住并朝着好的方向发展；未达预期表示应急决策效果不好或不明显，事态还很严重甚至进一步恶化。而决策主体要随时根据评估结果来决定是否调整提前制定的下一步应急决策。正因为每一次的评估结果分为达到预期和未达预期2种情况，突发事件情景演化路径也就可以分为乐观和悲观的2个方向。借鉴计算机数据结构里二叉树原理，可以形成突发事件情景演进路径，如图3所示。

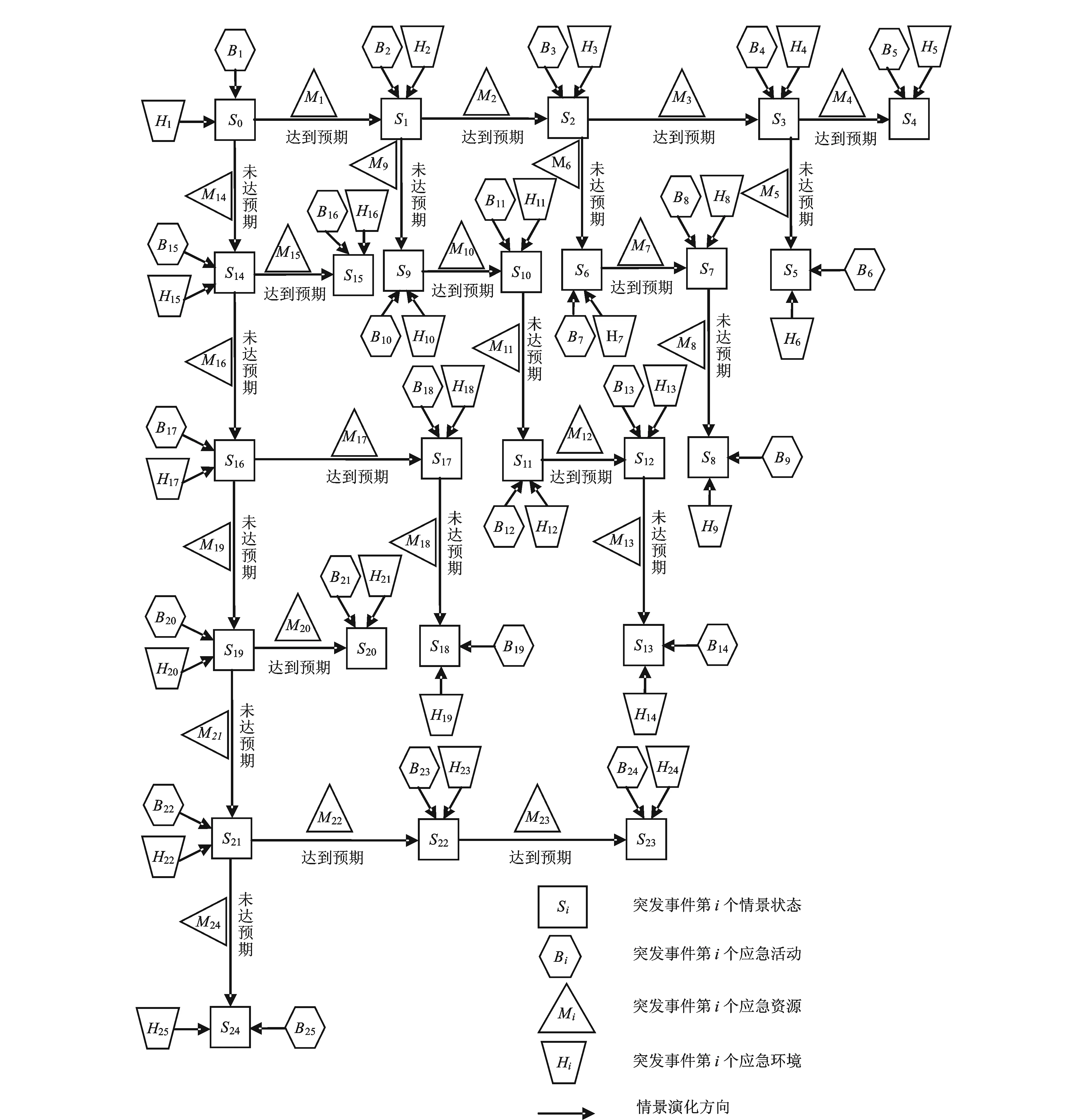
图3　突发事件情景演化路径Fig.3　Emergency scenario evolution path

在图3中，共有25个情景状态，其中S0为突发事件发生后的初始情景状态，S1到S24为发展演化情景。每一个情景状态Si(i从0开始)在应急活动Bi+1和外部环境Hi+1的作用下，在应急资源Mi的约束下，发生状态变化，实现情景演化。每一次的情景演化均有2条路径：乐观路径(达到预期)和悲观路径(未达预期)，其中横向向右的箭头(→)表示达到预期，情景演化朝着乐观的方向发展；纵向向下的箭头(↓)表示未达预期，情景演化朝着悲观的方向发展。由此，就形成一条最乐观的情景演化路径：S0→S1→S2→S3→S4，一条最悲观的情景演化路径：S0→S14→S16→S19→S21→S24。从以上分析可以看出，假设某个突发事件发生后，共发生n次情景演化，也就是说除了初始情景以外，还有n个情景状态，那么情景演化的路径理论上就有2n条，每一次应急决策都决定了突发事件朝着不同的方向发展，形成不同的演化轨迹和演化路径，而最乐观和最悲观的路径均只有一条。最乐观路径是最好的情况，也就是每一步决策都达到预期；最悲观路径正好相反，是最坏的情况，每一次决策均未达到预期。因此，由于突发事件发展的动态性，决定了应急决策主体在做每一次决策的时候都应非常谨慎，尽最大努力实现突发事件朝着最乐观的路径发展演化。

2　情景动态贝叶斯网络构建

2.1　动态贝叶斯网络

贝叶斯网络也称为信度网络、因果网络或概率图模型，是由代表变量节点以及连接节点的有向边构成的一个无环图，是目前不确定知识表达和推理领域最有效的模型之一。假设x为贝叶斯网络中因果关系的原因集合或父节点集，y为贝叶斯网络中因果关系的结果或称子节点，则有x→y，其中集合x包含n个元素，每个元素记为xi，则有xi∈x(i=1,2,…,n)。则全概率公式为：

P(y)=P(yx)

=P(yx1+yx2+…+yxn)

=P(yx1)+P(yx2)+…+P(yxn)。

(1)

从式(1)可以看出，全概率公式本质上是根据原因推结果。只要给出父节点的先验概率以及父节点到子节点的条件概率，就可以计算出子节点的后验概率。而贝叶斯公式与全概率公式正好相反，是在结果已经发生的情况下，推理某一原因的发生概率，表示式为

(2)

由于贝叶斯网络推理均隐含了一个条件独立性的前提假设，即对于一个给定节点的父节点集，该节点独立于它的所有非后代节点。因此，贝叶斯网络表示的所有节点的联合概率就可以表示为各节点条件概率的乘积，即

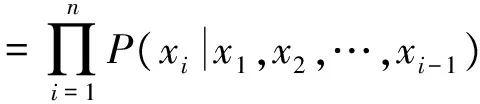
(3)

其中Pa(xi)为xi的父节点集。

所谓动态贝叶斯网络(Dynamic Bayesian Networks,简称DBN)，其实就是在静态贝叶斯网络的基础上增加了时间因素，使得时间推理与事件发展的时间上保持一致性与连续性，从而更符合客观现实。本质上动态贝叶斯网络可以看成是静态贝叶斯网络在时间轴上的展开式。假设现有T个时间片段，有n个隐藏节点和m个观测节点，xij表示第j个时间片段的第i个隐藏节点的状态，则有：

P(x11,x12,…,xT1,xT2,…,xTn|y11,y12,…,y1m,…,yT1,yT2,…,yTm)=

(4)

在式(4)中，xij为一个取值状态，每个变量的第一个下标i表示时间片段，第二个下标表示该时间片段内的第j个隐藏节点；yij为观测值，Pa(yij)为yij的父节点集合[17]。

2.2　情景网络构建

突发事件情景的动态贝叶斯网络构建，总体可以分为3个步骤：

2.2.1网络节点变量确定就是利用历史案例或者专家判断确定关键要素，关键要素数据化的结果就是网络节点变量。具体可以分步完成：第一步，根据对突发事件情景要素的分类方法分别采集情景要素；第二步，由领域专家对情景要素打分，同时可以辅助计算机图像识别与匹配技术，找出关键要素；第三步，根据关键要素的性质，确定变量的类型与取值集合。

2.2.2网络中节点变量因果关系的确定网络节点变量确定后，下一步就是确定节点变量之间的因果关系，并用有向边绘制出来，形成完整的突发事件情景网络。由于突发事件情景演化是一个连续的、动态的过程，因此，假设整个突发事件情景演化划分为T个时刻，分别为t0，t1，t2，…，tn，其中t0为突发事件发生的初始时刻，则整个突发事件情景演化的动态贝叶斯网络可以用图4表示。

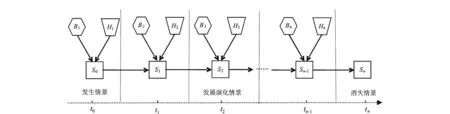
图4　突发事件情景演化的动态贝叶斯网络Fig.4　Dynamic Bayesian networks of emergency scenario evolution

2.2.3网络节点变量的概率确定与计算方法为了顺利实现情景状态的推演，必须先确定部分网络节点变量的先验概率或专家估计概率，然后利用先验概率或专家估计概率计算情景状态的状态概率，从而推演出下一情景状态出现的概率大小，完成情景推演过程。具体来说又可以分为两步：先验概率或专家估计概率的确定以及情景状态概率的计算。

3　实例应用

以2010年大连输油管道爆炸事件为例进行实证分析，检验本文提出的模型的正确性与有效性。

3.1　事件情景演化路径分析

根据前面对情景要素的划分，依据专家打分的结果，最终确定网络节点变量见表1。

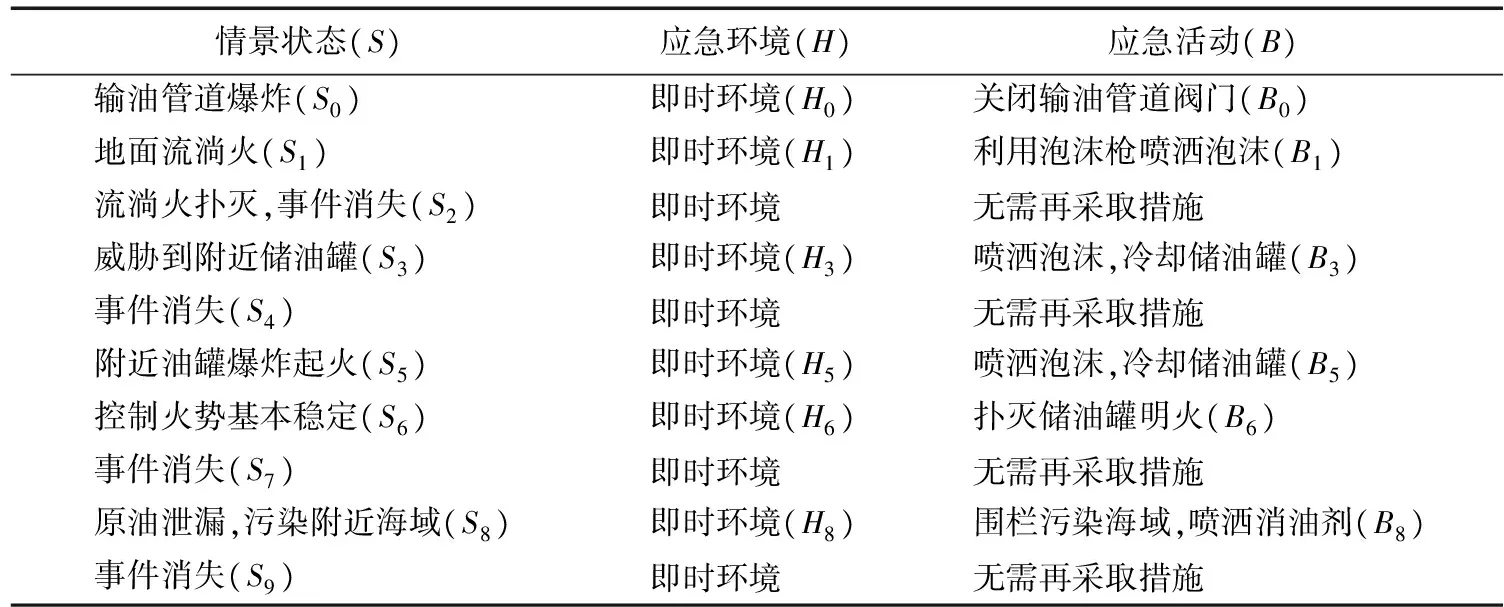
表1　大连输油管道爆炸事件情景要素[18]Tab.1　Scenario elements of Dalian oil pipeline explosion event[18]

将表1中的网络节点之间的关系表示出来，就可以形成该突发事件的情景演变路径，见图5。

3.2　事件情景概率分配与计算

根据网络节点的现实意义，确定网络节点变量的类型与取值集合见表2。

根据图5的演化路径，结合历史经验数据，对于没有父节点的节点确定先验概率，并对有父节点的网络节点变量，用专家打分的方法，确定条件概率,部分结果见表3。

表2　网络节点变量类型与取值集合Tab.2　Types and value sets of network node variables

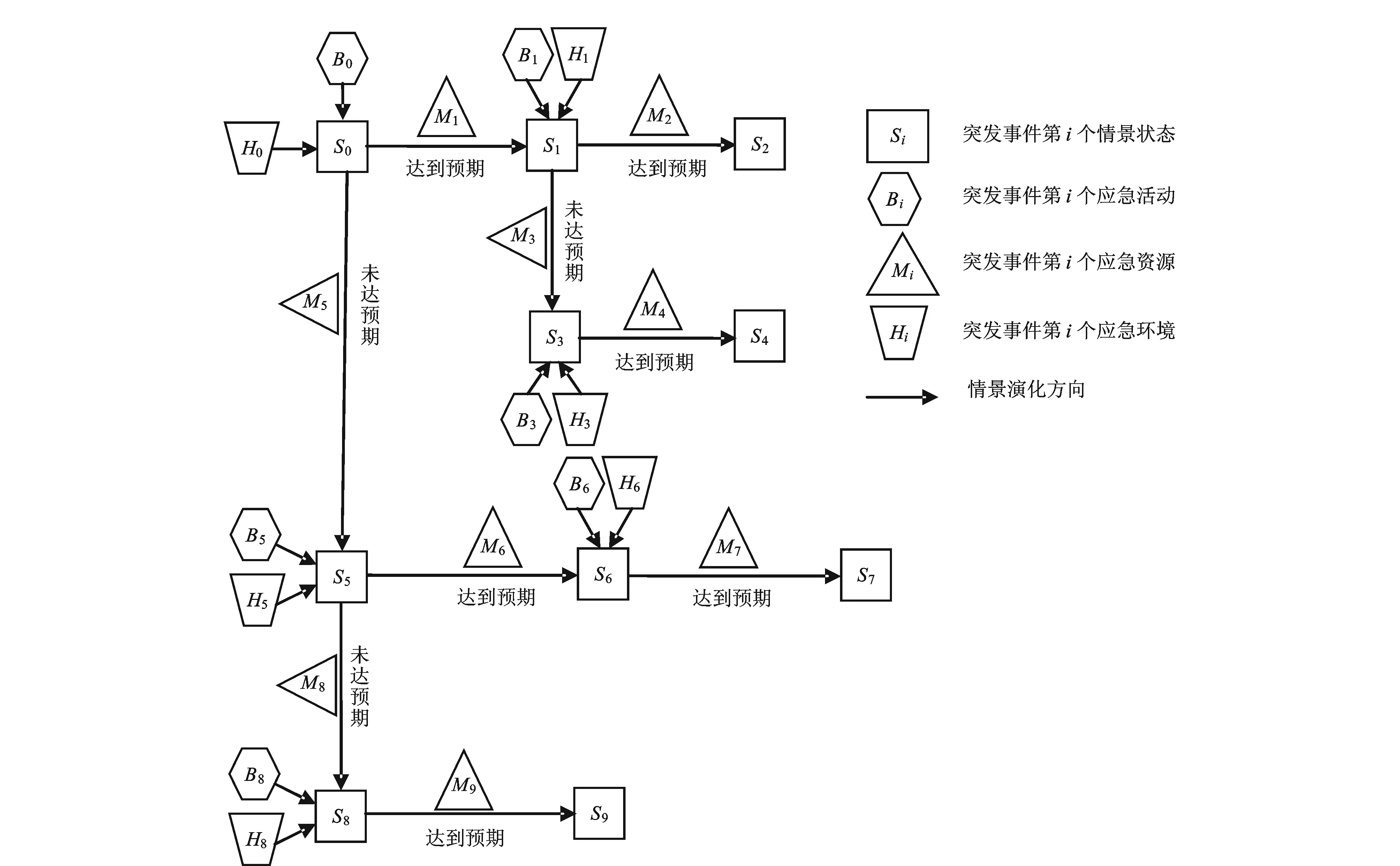
图5　大连输油管道爆炸事件情景演化路径Fig.5　Scenario evolution path of Dalian oil pipeline explosion event

利用式(1)和式(4)，计算S0的情景状态节点的概率如下：

P(S0=T) =P(B0=T)*P(H0=P)*P(S0=T|B0=T,H0=P)+P(B0=T)*P(H0=N)*P(S0=T|B0=T,H0=N)+P(B0=F)*P(H0=P)*P(S0=T|B0=F,H0=P)+P(B0=F)*P(H0=N)*P(S0=T|B0=F,H0=N)=0.95*0.7*0.95+0.95*0.3*0.8+0.05*0.7*0.7+0.05*0.3*0.4=0.890，则P(S0=F)=0.11。以此类推，分别计算出S1到S9的概率，如图6所示。

3.3　实证结果分析

从以上实证分析结果可以看出，发生概率最大的情景状态是输油管道爆炸(S0)、威胁到附近储油罐(S3)、附近储油罐起火(S5)、原油泄漏并污染附近海域(S8)等，发生概率分别为89.0%、86.4%、81.5%以及78.7%，计算结果基本符合突发事件现场实际状况，充分说明该模型的有效性与可行性。

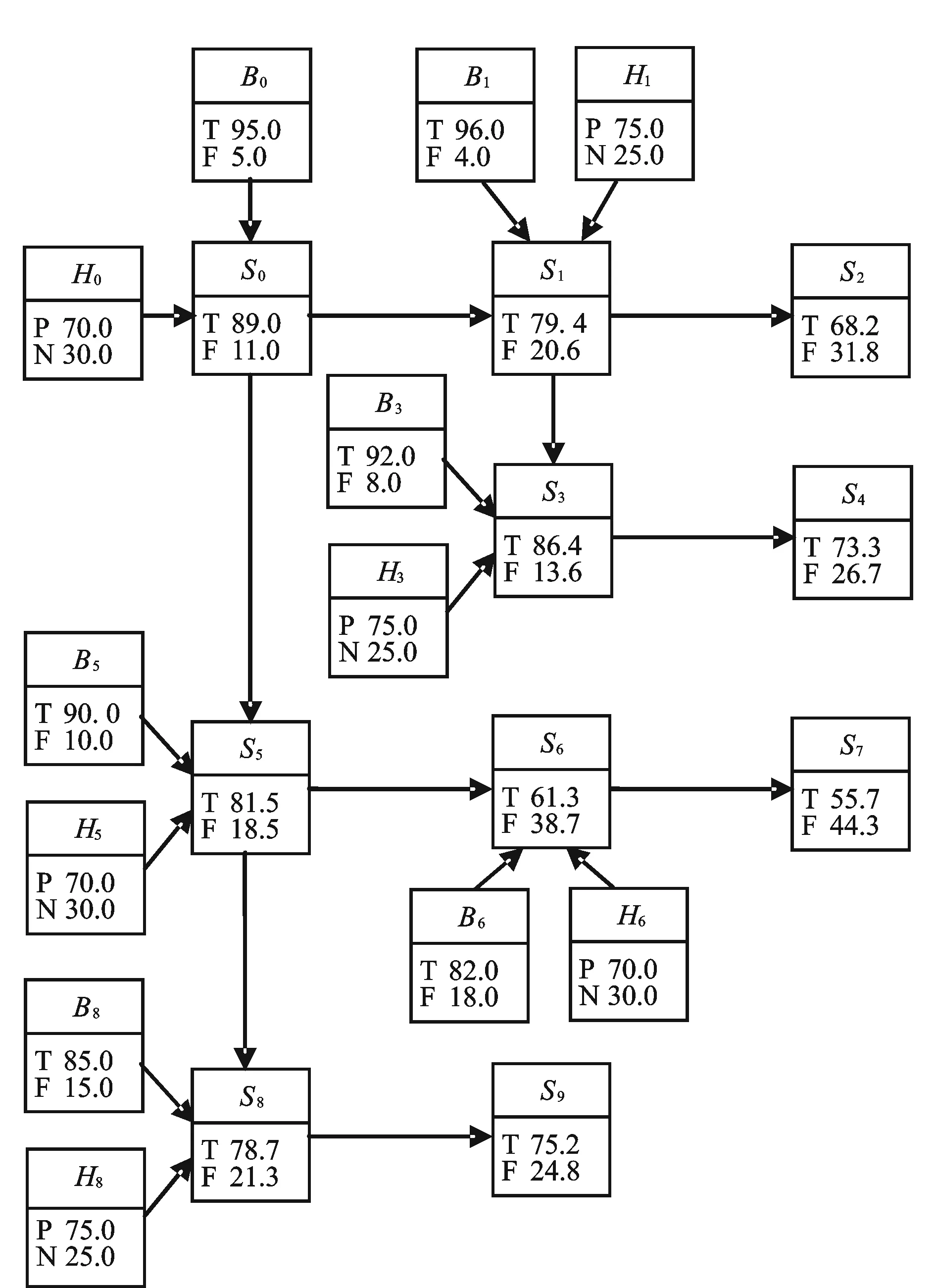
图6　大连输油管道爆炸事件情景推演Fig.6　Scenario deduction of Dalian oil pipeline explosion event

当然，每一次的应急活动和应急环境的变化，直接决定了情景演化的方向和路径，从理论上来讲，随着时间的推移，路径发展具有不确定性，而且有很多条路径，上述模型只是考虑了其中一部分路径演化情况。

4　结　论

(1)选取情景状态、应急活动、应急资源以及应急环境为关键要素，分析突发事件情景演化规律与路径，并基于动态贝叶斯网络理论构建情景网络，计算情景状态概率，从而推演情景发展趋势，以便提前采取措施。该方法思路清晰，应用简便，结果直观，有利于广泛推广应用。

(2)突发事件的发展演化的最大特点是不确定性和连续性，也是突发事件应急处置的最大障碍。基于动态贝叶斯网络的情景推演方法，不但可以通过贝叶斯网络的概率分配与计算解决不确定性问题，还可以利用动态来解决连续性问题，为突发事件情景推演提供了一种新的思路与方法。

(3)基于动态贝叶斯网络的情景推演方法的使用，需要合理确定网络节点变量，分配没有父节点的节点变量的先验概率，通过专家打分法确定条件概率。整个应用过程需要提供充分的情景信息、足够的历史经验数据以及丰富的领域专家知识等，每一个环节都会影响到最终结果的准确性。因此，如何降低情景推演过程中的主观成分，提高模型推演的精度，还有进一步研究的空间与必要性。

参考文献：

[1]KAHN H,WIENER A.The year 2000:A framework for speculation on the next thirty-three years [M].New York:Macmillan,1967.

[2]BARBAROSOGLU G,ARDA Y.A two-stage stochastic programming framework for transportation planning in disaster response[J].Journal of the Operational Research Society,2004,55(1):43-53.

[3]李仕明,刘娟娟,王博，等.基于情景的非常规突发事件应急管理研究：“2009突发事件应急管理论坛”综述[J].电子科技大学学报(社科版),2010,12(1):1-3.

LI Shiming,LIU Juanjuan,WANG Bo,et al.Unconventional incident management research based on scenarios:“The first international forum on incident management” (IFIM09) overview[J].Journal of UESTC (Social Sciences Edition),2010,12(1):1-3.

[4]姜卉,黄钧.罕见重大突发事件应急实时决策中的情景演变[J].华中科技大学学报,2009,23(1):104-108.

JIANG Hui,HUANG Jun.The study on the issues of scenario evolvement in real-time decision making of infrequent fatal emergencies[J].Journal of Huazhong University of Science and Technology,2009,23(1):104-108.

[5]武旭鹏，夏登友，李健行.非常规突发事件情景描述方法研究[J].中国安全科学学报，2014,24(4):159-165.

WU Xupeng,XIA Dengyou,LI Jianhang.Study on method for describing unconventional emergency scenario[J].China Safety Science Journal,2014,24(4):159-165.

[6]陈晨，俞政，张新梅.考虑应急活动的非常规突发事件情景刻画研究[J].中国安全科学学报，2014,24(10):163-169.

CHEN Chen,YU Zheng,ZHANG Xinmei.Study on characterization of unconventional emergency scenarios considering emergency activities[J].China Safety Science Journal,2014,24(10):163-169.

[7]盛勇，孙庆云，王永明.突发事件情景演化及关键要素提取方法[J].中国安全生产科学技术，2015,11(1):17-21.

SHENG Yong,SUN Qingyun,WANG Yongming.Emergency scenario evolution and extraction method of key element[J].Journal of Safety Science and Technology,2015,11(1):17-21.

[8]陈刚，谢科范，刘嘉，等.非常规突发事件情景演化机理及集群决策模式研究[J].武汉理工大学学报(社会科学版)，2011,24(4):458-462.

CHEN Gang,XIE Kefan,LIU Jia,et al.Research on the scenario evolution and group decision-making of unconventional emergency[J].Wuhan University of Technology(Social Science Edition),2011,24(4):458-462.

[9]袁晓芳，田水承，王莉.基于PSR与贝叶斯网络的非常规突发事件情景分析[J].中国安全科学学报，2011,21(1):169-176.

YUAN Xiaofang,TIAN Shuicheng,WANG Li.Scenario analysis of unconventional emergency based on PSR model and Bayesian networks[J].China Safety Science Journal,2011,21(1):169-176.

[10] 孙华丽，王循庆，薛耀锋.基于不同情景的群体性突发事件随机演化博弈模型[J].运筹与管理，2016,25(4):23-30.

SUN Huali,WANG Xunqing,XUE Yaofeng.Stochastic evolutionary game model for unexpected incidents involving mass participation based on different scenarios[J].Operation Research and Management Science,2016,25(4):23-30.

[11] 仲秋雁，郭艳敏，王宁，等.基于知识元的非常规突发事件情景模型研究[J].情报科学，2012(1):115-120.

ZHONG Qiuyan,GUO Yanmin,WANG Ning,et al.Research on unconventional emergency scenario model based on knowledge element[J].Information Science,2012(1):115-120.

[12] 张承伟，李建伟，陈雪龙.基于知识元的突发事件情景建模[J].情报杂志，2012(7):11-15.

ZHANG Chengwei,LI Jianwei,CHEN Xuelong.Emergency scenario model based on knowledge element[J].Journal of Intelligence,2012(7):11-15.

[13] 陈雪龙，卢丹，代鹏.基于粒计算的非常规突发事件情景层次模型[J].中国管理科学，2017,25(1):129-138.

CHEN Xuelong,LU Dan,DAI Peng.Hierarchical scenario model of unconventional emergency based on granular computing[J].Chinese Journal of Management Science,2017,25(1):129-138.

[14] 戎梅，赵廷弟，李晓磊.事故推演建模技术研究[J].航空学报，2008,29(6):1563-1569.

RONG Mei,ZHAO Tingdi,LI Xiaolei.Research on accident rehearsal modeling technique[J].Acta Aeronautica et Astronautica Sinica,2008,29(6):1563-1569.

[15] 李群.突发事件应急推演系统平台分析与设计[J].中国安全生产科学技术，2012,8(3):120-123.

LI Qun.Analysis and design of simulated emergency exercise system platform[J].Journal of Safety Science and Technology,2012,8(3):120-123.

[16] 杨保华，方志耕，刘思峰，等.基于GERTS网络的非常规突发事件情景推演共力耦合模型[J].系统工程理论与实践，2012,32(5):963-970.

YANG Baohua,FANG Zhigeng,LIU Sifeng,et al.Model of co-coupling in unconventional incidents based on GERTS network[J].Systems Engineering-Theory & Practice,2012,32(5):963-970.

[17] 史建国，高晓光.离散动态贝叶斯网络的直接计算推理算法[J].系统工程与电子技术，2005,27(9):1626-1630.

SHI Jianguo,GAO Xiaoguang.Direct calculation inference algorithm for discrete dynamic Bayesian network[J].Systems Engineering and Electronics,2005,27(9):1626-1630.

[18] 夏登友，钱新明，段在鹏.基于动态贝叶斯网络的非常规突发灾害事故情景推演[J].东北大学学报(自然科学版)，2015,36(6):897-902.

XIA Dengyou,QIAN Xinming,DUAN Zaipeng.Scenario deduction model of unconventional emergency based on dynamic Bayesian network[J].Journal of Northeastern University(Natural Science),2015,36(6):897-902.