车联网环境下的动态Robertson车队离散模型

姚志洪,蒋阳升

(1.西南交通大学交通运输与物流学院,四川 成都 610031; 2.西南交通大学综合交通运输智能化国家地方联合工程实验室,四川 成都 610031)

信号交叉口作为城市交通系统的重要组成部分,其运行状况直接影响城市交通系统的运营效果[1-2].在城市道路上,信号交叉口将连续的交通流分割成一股股的离散车队,由于车队中车辆行驶速度的差异性,在向下游交叉口行驶的过程中逐渐被离散化,出现的“离散车队”现象[3].在信号协调控制中,分析上游交叉口车辆离去流率与下游交叉口到达流率显得尤其重要,是信号协调控制优化的基础数据之一[4-5].

对于车队离散模型的研究,早在1956年Pacey[6]就分析路段车辆的速度分布,提出了基于速度服从正态分布车队密度离散模型;1964年Grace等[7]考虑车队密度的变化,在Pacey模型的基础上建立了描述车流密度变化的离散模型.但在协调控制中,不仅需要掌握车流密度的变化,更需要了解车流流量的变化规律.因此,1969年Robertson[8]在Hillier等[9]收集的数据基础上,提出了一种采用迭代计算的车队流量离散模型,其基本假设为车辆路段行程时间服从移位几何分布[10].由于该模型采用迭代计算速度快的优点,被广泛地应用于TRANSYT[8]、SCOOT[11]、SATURN[12]和TRAFLO[13]等信号配时优化软件或控制系统中.但Tracz[14]和Polus[15]通过收集大量车辆行程时间数据,发现其并不都是服从移位几何分布,正态分布或者对数正态分布拟合效果更好.随后的大多研究主要集中在Robertson模型的参数校正[16-18],并未提出新的模型.为增强模型的描述能力,姚志洪、巫威眺等[19-21]分别考虑行程速度的有界性和交通流的异质性,提出了基于截断概率分布和混合概率分布的车队流量离散模型.

以上车队离散模型均为事先假定路段行程速度或行程时间服从某种特定概率分布,基于此推导对应的车队离散模型.但由于这些模型的参数估计均基于历史调查数据,不能反映交通流的动态变化特征.随着车联网技术的发展,为信号控制领域提出了新的机遇[22-25].车联网技术通过路侧数据交互中心与车载装置之间每隔很短一段时间进行连续通讯来获取车辆信息.针对车联网应用技术,其需要两个通讯渠道,一个获取车流信息,一个则用于车辆的定位,目前需研究解决的技术问题主要在车辆定位的精度、延时、频率、信道数量以及与定位方式相关的路测定位设施建设及维护成本控制等问题上,本文仅探讨如何利用车联网技术提供的行程时间数据构建动态车队离散模型.

在Robertson模型中,需要调查获取路段行程时间数据,并基于此来估计模型的参数.因此,需要获得路段每辆车的行程时间数据,数据收集难度较大且费用较高;同时,由于其调查数据往往为历史数据,不能反映路段实际交通流的变化特征.而在车联网环境下,可实时动态收集路段的车辆的行程时间数据[24-25],并基于此可对Robertson模型参数进行动态滚动的估计与校正.

本文以经典的Robertson车队离散模型为例,采用车联网环境下提供的车辆行程时间数据对Robertson模型中的参数进行实时估计,并构建动态车队流量离散模型.文章第二部分为动态车队离散模型的构建和动态参数估计方法;第三部分为实际数据收集与模型比较分析;最后为结论与展望.

1　动态车队离散模型

1.1　Robertson模型

Robertson车队离散模型作为自适应信号控制系统TRANSYT和SCOOT中重要组成部分之一,该模型基本假设为车辆行程时间服从移位几何分布,通过上游离去流量分布预测下游到达流量分布.基于此对相邻交叉口信号协调配时优化进行研究.在文献[16]中,给出了Robertson车辆离散模型的基本形式,如式(1)～(2)所示.

(1)

qd(t)=Fqu(t-Ta)+(1-F)qd(t-1),

(2)

式中:qd(·)为下游交叉口某时间间隔内到达的车辆数;qu(·)为上游交叉口某时间间隔内离去的车辆数;Ta为上下游交叉口之间路段的最小行程时间;F为平滑系数.

在式(1)～(2)中,需要对模型的相关参数进行估计.根据文献[26]可知,路段最小行程时间和平滑系数可通过式(3)～(6)计算得到.

(3)

(4)

Ta=βμ,

(5)

(6)

式中:α为车队离散系数;β为行程时间系数;μ和σ分别为路段行程时间的均值和标准差,可根据历史调查数据计算获得[26].

1.2　动态Robertson模型

在静态Robertson车队离散模型中,F和Ta是根据历史调查数据计算得出,其值的大小与车辆的路段行程时间均值和车队离散系数有关.而在车联网环境下,车辆的行程时间可实时获取,因此为反映交通流的动态特征,这里采用滚动时间窗思想(即时间窗随着当前时刻的变化不断地滚动,假设当前时刻为tc,时间窗长度为T,则当前时刻对应的时间窗为[tc-T,tc],随着tc的变化,时间窗也随之变化,因此称为滚动时间窗)动态估计模型的参数,分别用Fi和Ta(i)来表示上游第i个周期(时间窗)离去车流所对应行程时间数据估计的模型参数值.

假设上游第i个周期tu时刻的离去流量为qu_i(tu),且其对应的模型参数为Fi和Ta(i),则根据Robertson模型[8]的原理,并引入动态参数,则有上游第i个周期车流在下游的分布为

(7)

式中:qd_i(td)为第i个周期下游交叉口时间间隔td内到达的车辆数.

基于此原理,依次类推,计算获得上游每个周期与其对应的动态参数,可运用Robertson模型计算到下游断面的车辆到达分布.

而对上游每个周期离去车辆在下游断面到达分布进行叠加,可得下游不同时刻的实际到达流量:

(8)

式中:M为总的周期个数.

可将式(7)和式(8)合并获得式(9),该公式的形式和Robertson模型一致,但其参数并不是固定不变,每个周期的参数都是动态变化,称为动态Robertson车队离散模型.

(9)

在车联网环境下,结合交叉口信号灯时间参数,很容易获取每个周期内每辆离去车辆在该路段的相关数据,如车辆的行程时间数据.若第i个周期内离去车辆数为Ni,则可结合式(3)～(6)对模型中的相关参数进行估计,估计公式如式(10)～(15).

(10)

(11)

(12)

(13)

Ta(i)=βiμi,

(14)

(15)

式中:μi、σi、αi、βi分别为根据第i个周期离去的车辆行程时间数据估计获得的路段车辆平均行程时间、行程时间标准差、车队离散参数、行程时间参数;tij为上游交叉口第i个周期第j辆离去车辆的行程时间.

本文中时间窗长度取值为上游交叉口的周期长度,即用上一周期的车辆行程时间数据估计下一周期车队离散模型的参数,这是考虑到交通流在很短的时间内不会发生突变,所以上一个信号周期的模型参数一定程度上能体现下一个信号周期的车流特征.

2　实例分析

2.1　实地调查与数据获取

在车联网环境中,车辆的行程时间数据很容易获得,基于此可对Robertson模型中的相关参数进行动态估计.在验证文中模型时,可采用拍摄车牌的方法获得车辆的行程时间数据,并结合交叉口的信号参数获得每个周期离去车辆的行程时间数据.基于这些行程时间数据验证Robertson模型采用动态参数的效果,以此来证明车联网环境下动态模型的合理性和有效性.文中选取了某市五山路进行调查,其中调查路段如图1所示.该调查路段包括上游交叉口和路段部分,路段为双向4车道,高峰时期公交车辆比例较大(其中包含14条公交线路).调查时间为上午7:30—11:20,根据流量特征可将调查时间分为时段1～4个时段，分别为7:30—8:20、8:20—9:30、9:30—10:20和10:20—11:20.同时,为了避免下游交叉口车辆排队过长时得不到车辆到达下游停车线的准确时间,在下游交叉口停车线前不远处的路段中间设置虚拟停车线,以获得车辆到达下游该断面的时间.因此,分别在上游交叉口离去断面和下游到达断面(距离650 m)设置摄像机,采用拍摄法获取每辆车的车牌号码,从而获得车辆的行程时间数据,数据精度为秒级,与车联网环境下获取的车辆行程时间精度一致,故而在车联网环境下,可直接对车路通信数据进行处理获得每辆车的行程时间数据.最终获得有效的车辆数据2 144条,其中各个时段的车辆行程时间特征数据如表1所示.

图1　调查路段示意Fig.1　Diagram of survey road segment

表1　行程时间相关参数Tab.1　Parameters of travel time

从表1中可知,4个时段公交车比例逐渐降低,行程时间的均值和标准差也随之减小.这说明公交车对路段车辆的行程时间分布影响较大,当公交车比例较大时,路段交通比较混乱,路段平均行程时间和标准差均较大,反之较小.而Robertson模型中的相关参数和路段行程时间的均值和标准差相关,因此,模型采用动态参数更能反映交通流运行特征.同时,考虑到车联网环境下,单个车辆的行程时间数据很容易获取,这为模型动态参数的估计提供了数据获取渠道.

2.2　模型动态参数分析

为证明文中模型使用动态参数的有效性和合理性,首先对调查数据分周期进行统计,获得129个信号周期的数据,求得每个周期所对应Robertson模型的参数,再按照静态Robertson模型求得4个时段模型的相关参数,如图2所示.

从图2中可知,不同时段平均行程时间变化较大,且不同周期内的平均行程时间波动更大;不同时段的平滑系数较为稳定,但也存在一定的波动.当交通流变化较大时,特别是早晚高峰,静态参数不能很好地表征交通流变化特征,因此,有必要采用新的技术和方法来动态估计模型的相关参数.而车联网环境下,很容易动态获取每个周期离去车辆的行程时间分布,这为模型动态参数的获取提供了渠道.基于这些数据动态实时地校正模型参数,使模型参数更能反映交通流的变化特征.

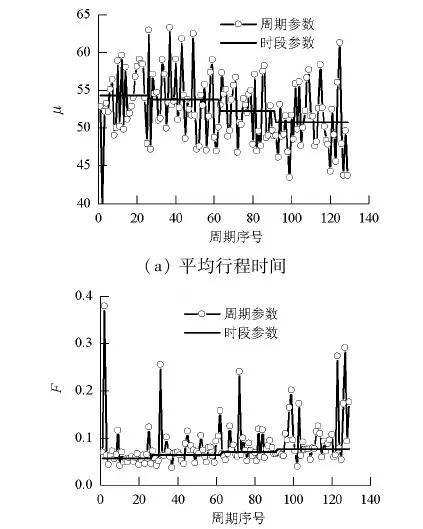
(b) 平滑系数图2　模型参数比较Fig.2　Comparison of model’s sparameters

2.3　上游交叉口离去流量

通过调查可知,调查路段上游交叉口采用自适应信号控制,其平均周期约为80 s.将各个时段的车辆按照周期进行汇总,统计精度为1 s,可求得上游交叉口车辆离去的平均流率分布和下游断面车辆到达的平均流率分布.其中上游交叉口车辆离去流率分布如图3所示.

由图3可知,4个时段流率变化较大,呈现典型的早高峰流量特征.也说明了早高峰交通流的波动特性,证明了模型采用动态参数的必要性.

2.4　下游交叉口到达流量

对于静态Robertson模型,其参数可按照文献[16]中的式(4)～(5)进行估计[16],4个时段的模型参数如表2所示.在车联网环境下,可以很容易获取当前时刻前一个时间窗长度的车辆行程时间数据,因此可基于前一个信号周期离去车辆的行程时间数据估计模型的参数,同时考虑到交通流在很短的时间内(如,一个信号周期)不会产生突变,因此,可以用上一个信号周期车辆行程时间估计的模型参数来替代当前信号周期的模型参数,基于此对未来车辆到达进行预测.由此可知,需要对每个周期进行一次参数计算,同时为了便于比较,对时段1～4分别计算下游断面的流率到达分布,4个时段下游实际观测流率分布数据、静态Robertson模型和文中动态模型计算的流率分布对比如图4所示.

(a)时段1(b)时段2(c)时段3(d)时段4图3　上游交叉口流率离去分布Fig．3　Diagramofflowrateleavingtheupstreamintersection

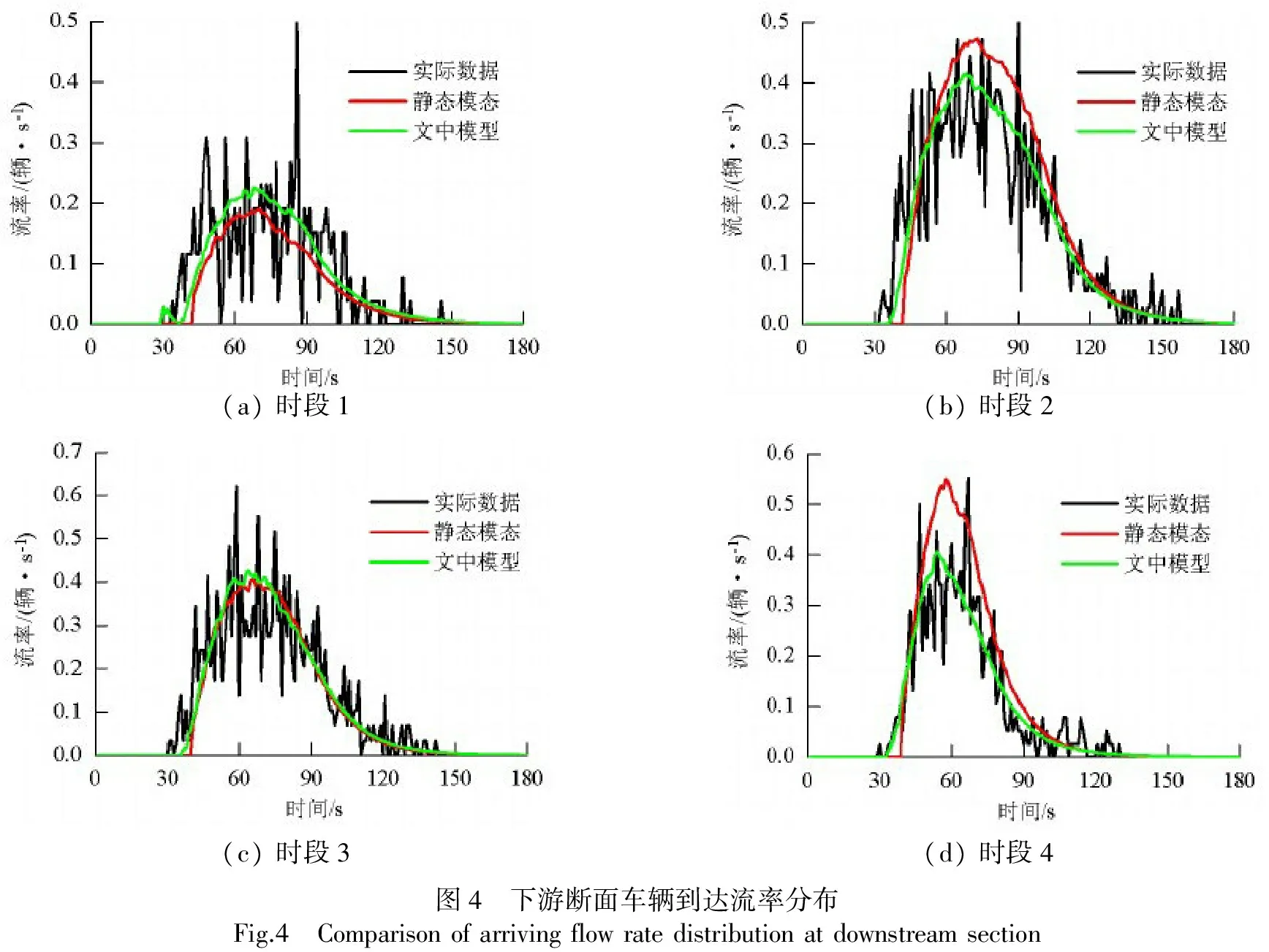
(a)时段1(b)时段2(c)时段3(d)时段4图4　下游断面车辆到达流率分布Fig．4　Comparisonofarrivingflowratedistributionatdownstreamsection

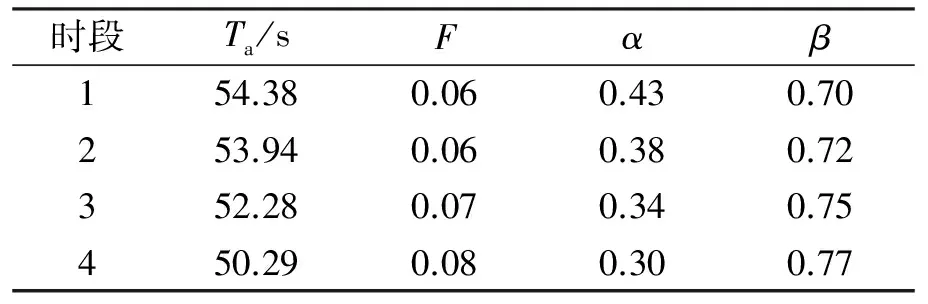
表2　Robertson模型参数估计表Tab.2　Parameters of Robertson’s model

2.5　模型比较分析

为定量地描述文中模型和静态Robertson模型的预测效果,分别计算图4中4个时段的本文模型和静态Robertson模型预测下游断面到达流率与实际观测到达流率的均方误差,计算结果如表3所示.

表3　两种模型均方误差表Tab.3　Mean squared error of two models

从图4和表3中分析可知：

(1) 从图4中可知,由于文中模型采用了动态参数,能够更准确地估计行程时间参数,所以图中对于车辆刚开始到达下游的时间点,本文模型拟合得更好;而静态Robertson模型采用的是静态行程时间参数,不能很好地反映下游断面车辆到达流率特征.

(2) 从图4中的4个时段分析可知,当交通流波动较大时,本文模型拟合效果更好.其中时段2和4下游到达流率波动较大;从表3中可知,本文模型较Robertson模型预测均方误差分别减少了42.60%和58.83%.

(3) 从图4中可知,本文模型计算得到的下游流率分布曲线与实际观测分布曲线更接近,同时表3中的均方误差计算结果也体现了这点.表3中,4个时段的平均均方误差较静态Robertson模型减少了30.68%.分析可知,文中模型采用动态参数能够很好地反映交通流的变化特征,而静态Robertson模型采用的静态参数,所以预测效果较差.

3　结　论

车联网环境下,车辆的路段行程时间很容易实时获取.本文充分利用车联网环境下的车辆行程时间数据,构建了动态Robertson车队离散模型,采用车辆的行程时间数据实时估计模型的参数,使模型参数动态化.通过与调查数据、静态Robertson模型对比,可以得到以下结论:

(1) 本文中通过研究时段参数和周期参数对模型结果的影响,证明了模型参数随着交通流的波动而波动,即使用动态参数更能体现交通流特征;

(2) 本文模型能够更好地反映交通流的变化特征,其计算结果与实际观测结果更接近;

(3) 与静态Robertson模型相比,本文模型预测的均方误差减少了30.68%.

从调查数据分析可知,路段的行程时间跟公交车辆比例存在一定的关系,未来可采用车联网技术获取海量数据的基础上,分析模型动态参数与其他因素(公交比例、天气等)之间的关系.同时探讨其他动态车队模型的参数估计和建模研究.

致谢:西南交通大学优秀博士学位论文培育项目(D-YB201708).

参考文献:

[1]ROESS R P,PRASSAS E S,MCSHANE W R.Traffic engineering:united states edition[M].Englewood Cliffs:Prentice-Hall,2010:5-10.

[2]JIANG Yangsheng,YAO Zhihong,LUO Xiaoling,et al.Heterogeneous platoon flow dispersion model based on truncated mixed simplified phase-type distribution of travel speed[J].Journal of Advanced Transportation,2016,50:2160-2173.

[3]BONNESON J,PRATT M,VANDEHEY M.Predicting arrival flow profiles and platoon dispersion for urban street segments[J].Transportation Research Record:Journal of the Transportation Research Board,2010,2173:28-35.

[4]JIANG Yangsheng,YAO Zhihong,DING Xiao,et al.Mixed platoon flow dispersion model based on truncated mixed phase distribution of speed[C/OL]∥Transportation Research Board of the National Academies.[2016-05-17].https://pubsindex.trb.org/view/2016/C/1393937.

[5]JIANG Yi,LI Shuo,SHAMO D E.A platoon-based traffic signal timing algorithm for major-minor intersection types[J].Transportation Research Part B Methodological,2006,40(7):543-562.

[6]PACEY G M.The progress of a bunch of vehicles released from a traffic signal[R].London:Transport and Road Research Laboratory,1956.

[7]GRACE M J,POTTS R B.A theory of the diffusion of traffic platoons[J].Operations Research,1964,12(2):255-275.

[8]ROBERTSON D I.TRANSYT:a traffic network study tool[R].London:Transport and Road Research Laboratory,1969.

[9]HILLIER J A,ROTHERY R.The synchronization of traffic signals for minimum delay[J].Transportation Science,1967,1(2):81-94.

[10]SEDDON P A.Another look at platoon dispersion 3:the recurrence relationship[J].Traffic Engineering and Control,1972,13(10):442-444.

[11]HUNT P,ROBERTSON D,BRETHERTON R,et al.SCOOT:a traffic responsive method of coordinating signals[R].London:Transport and Road Research Laboratory,1981.

[12]HALL M,WILLUMSEN L G.SATURN:a simulation-assignment model for the evaluation of traffic management schemes[J].Traffic Engineering & Control,1980,21(4):81-94.

[13]LIEBERMAN E B,ANDREWS B.TRAFLO:a new tool to evaluate transportation system management strategies[J].Transportation Research Record:Journal of the Transportation Research Board,1980,772:9-15.

[14]TRACZ M.The prediction of platoon dispersion based on rectangular distribution of journey time[J].Traffic Engineering & Control,1975,16(11):25-36.

[15]POLUS A.A study of travel time and reliability on arterial routes[J].Transportation,1979,8(2):141-151.

[16]YU Lei.Calibration of platoon dispersion parameters on the basis of link travel time statistics[J].Transportation Research Record:Journal of the Transportation Research Board,2000,1727:89-94.

[17]BIE Yiming,LIU Zhiyuan,MA Dongfang,et al.Calibration of platoon dispersion parameter considering the impact of the number of lanes[J].Journal of Transportation Engineering,2013,139(2):200-207.

[18]PAUL B,MITRA S,MAITRA B.Calibration of Robertson’s platoon dispersion model in non-lane based mixed traffic operation[J].Transportation in Developing Economies,2016,2(2):1-14.

[19]姚志洪,蒋阳升,吴云霞,等.基于速度服从混合PH分布的车队离散模型[J].交通运输系统工程与信息,2016,16(3):133-140.

YAO Zhihong,JIANG Yangsheng,WU Yunxia,et al.Platoon dispersion model based on mixed phase distribution of speed[J].Journal of Transportation Systems Engineering and Information Technology,2016,16(3):133-140.

[20]姚志洪,沈旅欧,巫威眺,等.基于行程时间分布的异质交通流车队离散模型[J].中国公路学报,2016,29(8):134-142,151.

YAO Zhihong,SHEN Lüou,WU Weitiao,et al.Heterogeneous traffic flow platoon dispersion model based on travel time distribution[J].China Journal of Highway and Transport,2016,29(8):134-142,151.

[21]巫威眺,沈旅欧,靳文舟.基于速度截断分布和流量的车队离散模型[J].西南交通大学学报,2014,49(1):126-133.

WU Weitiao,SHEN Lüou,JIN Wenzhou.Platoon flow dispersion model based on truncated normal distribution of speed[J].Journal of Southwest Jiaotong University,2014,49(1):126-133.

[22]LEE J,PARK B.Development and evaluation of a cooperative vehicle intersection control algorithm under the connected vehicles environment[J].IEEE Transactions on Intelligent Transportation Systems,2012,13(1):81-90.

[23]FENG Yiheng.Intelligent traffic control in a connected vehicle environment[D].Arizona:The University of Arizona,2015.

[24]TIAPRAPRASERT K,ZHANG Yunlong,WANG Xiubin,et al.Queue length estimation using connected vehicle technology for adaptive signal control[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(4):2129-2140.

[25]FENG Yiheng,HEAD K L,KHOSHMAGHAM S,et al.A real-time adaptive signal control in a connected vehicle environment[J].Transportation Research Part C Emerging Technologies,2015,55:460-473.

[26]YU Lei.Real-time calibration of platoon dispersion model to optimizethe coordinated traffic signal timings in ATMS networks[R].Houston:Center for TransportationTraining and Research,Texas Southern University,Houston,1999.