基于价格规制和第三方物流参与的三级供应链协调机制研究

2018-04-11王夫冬周梅华

统计与决策 2018年6期

王夫冬，周梅华

（1.中国矿业大学管理学院，江苏徐州 221116；2.中国矿业大学徐海学院，江苏徐州 221008）

0 引言

现代管理技术随着信息技术的快速发展，在实际中应用广泛，在市场竞争中，客户的需求也呈现出个性化、多样化，单个企业若按通过传统生产运作模式发展，则其生存会越来越难。在今后，各大企业之间的竞争发生变化，向着供应链和供应链竞争的方向发展[1-3]。在这种情况下，供应链上的节点企业起到关键性的作用，并认识到提高自身核心能力的重要性，同时将非核心业务采取外包这种新的模式，由第三方服务提供者负责，在供应链管理过程中，对现代高效率的管理方式越来越重视，而第三方服务则成为最重要的标志[4]。在此种状况下，企业越来越倾向于选择第三方物流，使其完成其高效物流的运作，节点企业之间通过协同合作，使供应链协调更加趋于合理[5-9]。在供应链出现之前，企业自身为独立经济体，经营活动目标及出发点就是使自身收益最大化[10]。因此，若在节点企业之间无有效激励机制进行约束，则合作可能会无实际意义，这会造成供应链管理优势很难得到发挥。我国物流企业大多为中小型，因此对于分包商和第三方物流提供者而言，合作非常重要[11]。

目前，对单一物流、TPL提供商、零售商需求企业间的协调问题研究较多，对在价格规则下，供应链模式下，上、下游企业、TPL提供商、零售商的协调机制、博弈关系和研究较少。因此，本文在前人研究成果的基础上，基于价格规制，对第三方物流参与的三级供应链协调机制进行了研究，根据价格规制，以增加渠道总收益，提高供应链整体服务水平，实现参与各方共赢为目的，使用简化的MCRS方法，对零售商、TPL提供商、第三方物流提供者的供应链模型及其协调问题进行了分析，为供应链的协调运作提供了指导。

1 价格规制行为对产品定价分析

1.1 投资回报率模型

在某一特定时期内，假设只有一种产品作为企业定价的依据，那么在价格规制模型中，投资回报率的产品价格用公式（1）表示：

若包含n种产品作为企业定价的依据，则其价格规制模型用公式（2）表示：

在公式（1）和公式（2）中，P表示产品价格，其值由C的大小确定，成本费用用C表示；与产品有关的变量用S表示；投资回报率基数用RB表示。

在产品只有一种时，企业投资额加上政府规定的回报率及企业的成本就等于产品规制价格(P)；当有多种产品时，所有产品的综合价格就是产品规制价格。通常情况下，在估算企业的成本费用时则比较容易，在规制者对企业价格规制时，比较难的是对投资回报率基数(RB)、投资回报率(S)的确定。关于投资回报率，就是找到一个恰当的S值，对于正常的投资回报，企业能够获取；投资回报率基数要对资本计量方法、投资范围进行合理确定，在一定的S值下，投资回报率基数直接关系着企业的利润总额。

1.2 最高限价模型

英国采取RPI-X模型进行最高限价规制，RPI所代表的是零售价格指数，也称其为通货膨胀率，X所代表的是以一定时间为周期，生产效率增长的比率，规制者确定X值。如某年的通货膨胀率为8%，也就是RPI=8%，X固定为5%，也就是X=5%，则企业提价幅度为RPI-X=8%-5%=3%。假设在本期，企业价格是Pt；在下期，企业规制价格是Pt+1，假设RPI-X＞0，在现价基础上，企业提价的最高幅度是RPI-X；假设RPI-X＜0，则意味着企业必须将价格降低，降价最低幅度是RPI-X。英国最高限价规制模型比较适用于单一产品及服务综合规制价格水平或服务规制价格水平。通常采用加权平均价格形式，进行多种产品的综合最高限价，产品所创造的收益由该产品价格权数确定。

2 模型描述

通常情况下，一般的模型包括TPL服务提供商、零售商、制造商的供应链。本文通过单一零售商供应链转化为多零售商供应链结构，并对其进行优化，使得实际情况和模型更加接近。假设一个单周期供应链构成包括制造商（M）一个、TPL提供商（L）一个、独立零售商（R）共有n个。制造商将单一产品供应给零售商，TPL提供商完成产品的运输、搬运、包装、装卸等，零售商销售产品给顾客。在供应链上，各节点企业先由制造商进行决策，选择使自身最大利润的批发价pm；在给定的批发价下，TPL提供商随后对服务价格pi进行决策，且pi使其自身获取最大利润；根据TPL提供商、制造商的报价，零售商最后对能使其自身获取最大利润的零售价进行选择，零售商及制造商共同承担订购数量qi◦pi、服务价格pi，其中pi承担比例为θ1，qi◦pi承担比例为θ2。零售的单位成本为cr，TPL提供商单位成本为cl，制造商单位成本为cm。

作如下假设方便研究：

假设H1：在供应链中，各节点企业之间信息是完全对称的。

假设H2：在供应链中，各节点企业全部是风险中性者，各节点企业自身利润最大化。

假设H3：在供应链中，零售价格及市场需求呈线性关系函数p=a-bQ，其中a、b均为常数，同时a＞0,b＞0。

假设H4：在供应链中，各零售商得到的批发价、单位成本全部相等。

假设H5：在供应链中，TPL提供商物流能力、制造商具有无限大生产能力，能及时满足对订单的需求。

3 建模与求解

3.1 独立决策模型

TPL提供商、零售商、制造商独立决策时，未有任何联盟形成，这时用公式（3）表示主从对策模型：

通过逆向归纳法，对公式（3）进行求解，获得各节点企业的定价。

供应链整体利润表示为：

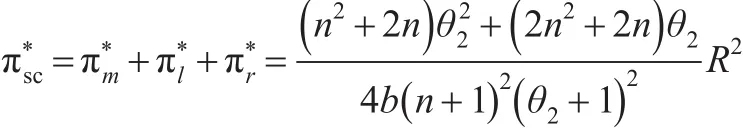
其中R=a-cr-cm-cl＞0

3.2 联合决策模型

本文建立零售商、TPL提供商、制造商组成的三级供应链合作的类型，供应链在联合决策时，假设TPL提供商参与有可能出现的4种联盟方式，即：TPL提供商和制造商的小联盟，零售商及TPL提供商的小联盟，零售商及制造商的小联盟，零售商、TPL提供商、制造商的大联盟体。

（1）TPL提供商和制造商的小联盟

TPL提供商及制造商形成小联盟联合决策，在该小联盟中，零售商没有参与，其主从对策模型用公式（4）表示：

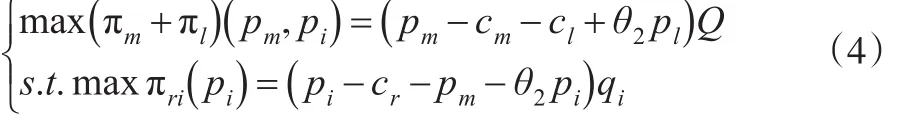
（2）零售商及TPL提供商的小联盟

零售商及TPL提供商形成小联盟联合决策，在该小联盟中，制造商没有参与，其主从对策模型用公式（5）表示为：

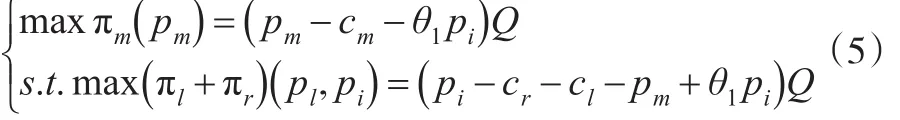
（3）零售商及制造商小联盟

小联盟联合决策由制造商、零售商组成，TPL提供商在该小联盟中未参与，其主从对策模型用公式（6）表示为：

（4）零售商和TPL提供商及制造商的大联盟体

大联盟体由零售商、制造商、TPL提供商组成，三者联合进行决策，公式（7）表示大联盟的利润函数：

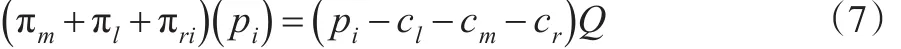
3.3 模型分析

（1）模型分析结论1

需要进行独立决策时，θ2影响对产品的市场零售价产生影响，如果θ2增大，则零售价减小，而销售量则处于增大状态；如果θ2增大，将产生较大的影响力，零售商和TPL服务提供商都会发生变化，与制造商供应链的利润均均呈增大趋势；在θ2=1时，供应链和各企业利润达到最大。

从以上可知，由于θ2≤1，因此，πm,πl,πri全部为θ2的增函数；由于 πsc=πm+πl+πr，因此，θ2的增函数是 πsc，πm,πl,πri,πsc在θ2=1时，全部获得最大值。

经过模型分析后并得出结论1,如果由TPL提供商承担起物流服务的责任，如果制造商所需要负责的费率和θ1越低时，零售商批发价格则处于较低状态，在这种情况下降低零售价，提高销售量，即零售价降低速度小于销售量增加速度，从而使得各方利润均得到增加。

（2）模型分析结论2

零售商在对销售价格进行独立决策时，如果n增大，则销售价格处于降低状态，而订购量则会受到n增大的影响而呈现出增大；从制造商和TPL提供商的利润来看，由于n增大而增加，但是需要注意的是如果n处于增大状态，则零售商所获取的利润会处于减少状态。

通过模型分析，结论2表明如果零售商数量增加，制造商会采取相应的措施，使零售价格降低，可以使产品销售量显著增加，达到提高利润的目标，使得自身的利润得到增加。

（3）模型分析结论3

当零售商、TPL提供商、制造商三方组成一个供应链大联盟时，可使供应链整体利润获得最大；当三方没有组成任何联盟时，则会导致供应链的整体利润具有最小值；如果制造商与TPL提供商之间的关系发生变化，组成小联盟局部合作的情况下，供应链整体利润则呈现为最大值，即满足公式（8）：

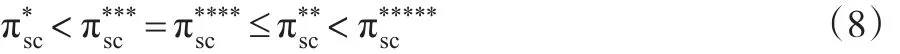
当n=1时，，这表明是成立的。

通过模型分析，通过结论3可知，在供应链中，小联盟和节点企业如果在进行独立决策合作的情况下，就会有双重边际效应产生，通过零售商、TPL提供商、制造商三方形成大联盟体的合作，会导致零售价格发生变化，处于降低状态，销售量有所增加，使系统利润显著提高。当TPL提供商和制造商在进行局部合作形成小联盟，在这种情况下供应链整体所获取的利润最大。

4 联合决策的收益分配

4.1 NASH谈判模型收益分配

如果各方都没有采取联盟形式，在本次研究中，设定收益谈判点分别为，按照HNAS谈判模型，建立进行合作的三方均收益的谈判模型，见公式（10）、（11）所示：

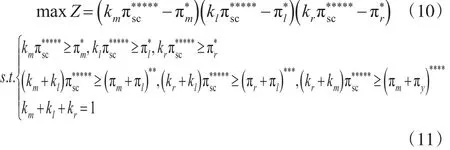
4.2 最小核心法收益分配

根据最小核心法的基本思想，建立公式（12）所示的线性规划模型：

4.3 简化的MCRS法收益分配

根据简化的MCRS法的基本思想，建立公式（13）所示的线性方程组：

5 算例分析

本文在进行算例分析时，根据参考文献中的相关数据[12]，设置各参数为a=30，b=0.2，cm=5，cl=2，cr=3，θ2=0.8。

5.1 θ2与各企业价格及供应链利润关系

θ2代表零售商所需要承担的物流费用比重，θ2影响力较大，不同企业的定价与订购数量都会受其影响。

由下页表1可知，随着θ2的增大，产品零售价格、物流服务价格、批发价格都随之降低，订购量则随之增大，同时，Q增大的速度要比pi降低的速度大。

表1 θ2与订购量及各企业价格关系

表2 θ2与各企业及供应链利润关系

表2为θ2与各企业、供应链的利润关系，由表2可知，随着θ2的增大，供应链总利润和各节点企业利润均随之增加，其中在θ2=1时，可达到最大利润。

5.2 n的大小的影响

各企业利润和定价及订购量在供应链中均受到n大小的影响，见表3。

表3 订购量变化表

由表3可知，在进行独立决策时，如果制造商和TPL提供商之间形成小联盟关系的情况下，将会对订购量产生影响，n增大则订购量增大。但是如果大联盟和小联盟把零售商也纳入其中后，则n发生变化，而订购量则处理较为稳定状态。

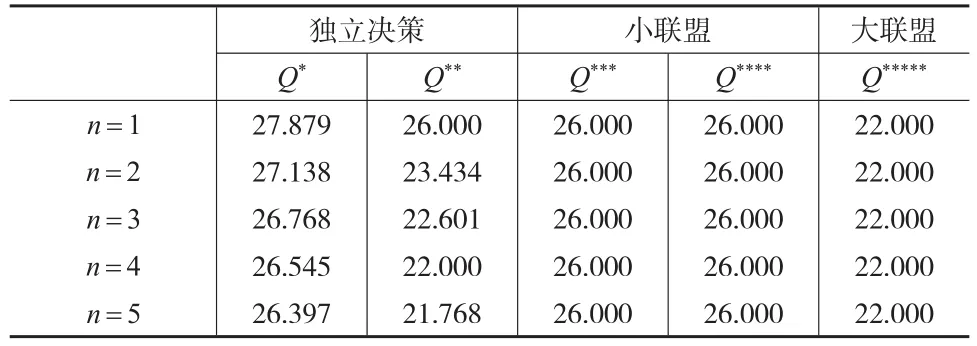
表4 市场零售价变化表

表4为市场零售价受n影响的变化表，由表4知，在TPL提供商、制造商和独立决策形成小联盟时，随着n的增大，产品市场零售价均随之降低；当大联盟或小联盟纳入零售商时，零售价不受n大小的影响。

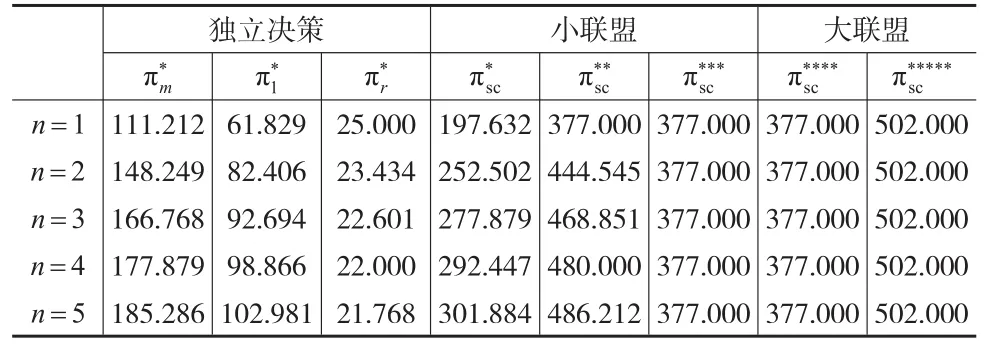
表5 供应链总利润和各企业利润变化表

表5为供应链总利润、各企业利润受n影响的变化表，由表5知，随着n的增大，供应链总利润随之增加；当大联盟或小联盟纳入零售商时，n的影响力较小，供应链总利润比较稳定。在独立决策的情况下，如果TPL提供商与制造商利润受到n增大的影响，而处于增加状态时，零售商利润会受到影响而随之减少。因此适当将零售商数量增大，可增加系统和制造商的利润。

5.3 不同分配方法对各企业的利润的影响

在独立决策时，订购量最小，零售价最高，系统总利润最小；在大联盟合作时，订购量最大，零售价最低，系统总利润最大；制造商和TPL提供商组成小联盟合作时，系统具有最大总利润。本文采用EXCEL和LINGO计算不同分配方法下各企业的利润、增长百分比。表6为不同分配方法下各企业利润，表7为不同分配方法下各企业的利润增长百分比。

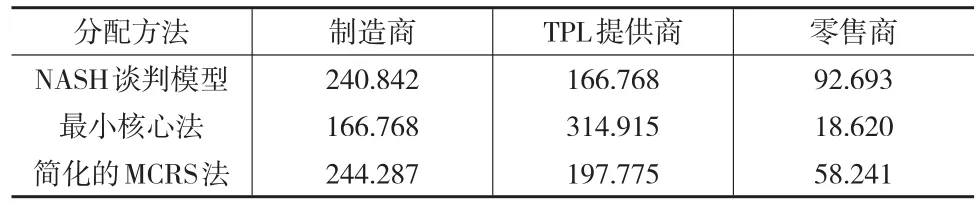
表6 不同分配方法下各企业的利润

表7 不同分配方法下利润增长百分比

由表6和表7知，在对收益进行分配时，需要采取有效的方式进行，以最小核心法为例，也就是说供应链增加收益是由TPL提供商所占有的，但对于制造商和零售商来说，收益并没有得到改进，由此可知在利润分配中并不适合采用最小核心法。在三方之间可作为协商基础。采用简化的MCRS法、NASH谈判模型时，各方利润均有较大幅度的增长。TPL提供商和制造商获取最大收益，是在简化的MCRS的方法下才能够实现，也就是说零售商在NASH谈判模型下，才能够获取最大收益。因而，在进行三方谈判时，零售商采用NASH谈判模型，TPL提供商和制造商则采用简化的MCRS方法。在本文中，供应链联盟在进行收益分配时采用简化的MCRS方法。作为零售商，在MCRS方法下与在TPL提供商和制造商两种情况下，MCRS方法下增长幅度最大。从本算例可知，经过简化处理的MCRS方法具有较高的科学性，是理想的收益分配模式，采用这种方法TPL提供商收益分配系数为0.497、零售商收益分配系数为0.217，制造商收益分配系数为0.589。