基于弹性薄板理论的充填挡墙厚度新模型
2018-04-11张爱卿吴爱祥韩斌王贻明常宝孟王虎武栓军
张爱卿,吴爱祥,韩斌,王贻明,常宝孟,王虎, 2,武栓军, 2
基于弹性薄板理论的充填挡墙厚度新模型
张爱卿1,吴爱祥1,韩斌1,王贻明1,常宝孟1,王虎1, 2,武栓军1, 2
(1. 北京科技大学 土木与资源工程学院,北京,100083; 2. 金川集团有限公司,甘肃 金昌,737100)
为了准确计算充填挡墙的厚度,选取一次充填高度和充填挡墙混凝土抗拉强度作为影响因素,基于弹性薄板理论,建立钢混充填挡墙厚度力学模型,推导一次充填高度、混凝土抗拉强度与充填挡墙厚度的关系式。以金川二矿区为工程分析实例,采用控制变量法(CVM)研究一次充填高度和混凝土抗拉强度与充填挡墙厚度的变化规律。研究结果表明:在充填挡墙尺寸和充填料浆物理力学参数一定的前提下,当一次充填高度不变时,充填挡墙的厚度随着混凝土抗拉强度的增大逐渐减小,呈1/2幂次关系;当混凝土抗拉强度不变时,充填挡墙的厚度随着一次充填高度的增加逐渐增大,呈1/2幂次关系。通过与已有充填挡墙厚度理论方法和结果比较,验证了新模型的正确性和合理性。
充填挡墙;力学模型;弹性薄板理论;变化规律
充填挡墙的设计不仅要在强度上承受来自充填料浆的作用,而且要在结构上满足抵抗矿区爆破震动和充填料浆滤水的要求[1−5]。其强度和结构与矿山充填工艺密切相关,影响充填质量、生产能力和成本效益[6−7]。但是,由于每个矿山井下充填条件的复杂性,所选用的充填挡墙类型并不完全相同。目前,在国内针对充填挡墙厚度计算多采用工程经验类比法或是引用《采矿设计手册》[8]中“井巷工程卷”的防水闸门设计公式,尚无完整的充填挡墙设计规范可以参考[9−12]。国内外学者对充填挡墙受力分析和数值模拟方面进行了大量的研究。王丽红等[13]对原有单一结构的混凝土充填挡墙进行了优化改进以及工艺研究,针对不同尺寸巷道采用不同形式的充填挡墙;汪海萍等[14]提出了采场充填挡墙的具体实施方案,并对充填挡墙进行受力分析及力学参数计算,参考《采矿设计手册》中“井巷工程卷”的防水闸门设计来计算充填挡墙的结构厚度。袁世伦[15]用有限元法对采场围岩和充填体的应力分布状况进行了研究,按充填料浆3种不同力学性质状态对充填挡墙进行了受力分析和计算。NORTJÉ 等[16]针对充填过程中挡墙的受力进行分析,并对其进行设计。KANOWNA等[17]对已有充填挡墙的厚度由40 cm调整至35 cm,并利用FLAC3D软件进行模拟分析,结果表明可保证其正常使用。对于充填挡墙厚度理论方面的研究,国内外的矿山虽已有成功案例,但对于充填挡墙厚度力学模型鲜有研究。本文作者选取一次充填高度与充填挡墙混凝土抗拉强度作为充填挡墙厚度的影响因素,基于弹性薄板理论,建立钢混充填挡墙厚度力学模型,并对其进行理论分析,以金川二矿区某巷道处钢混充填挡墙为工程分析实例,分析一次充填高度与充填挡墙混凝土抗拉强度对充填挡墙厚度的影响规律,并与已有充填挡墙厚度理论方法、结果相比较,验证新模型的正确性及合理性。
1 充填挡墙厚度力学模型理论分析
分析近些年钢混充填挡墙工程实例,可以发现充填挡墙厚度远小于其高度和长度,根据弹性力学理论,当充填挡墙尺寸已达到或超过充填挡墙厚度的5~8倍时,充填挡墙可近似按薄板处理,得出的结果在工程上也是可用的。因此,对于充填挡墙厚度力学模型作以下假设[18]:
1) 假设充填体是均质、各向同性材料。在实际进行充填过程中,采空区并不是一次性充满,而是分层充填的。为进行理论求解,这里假设充填挡墙形成后,充填过程一次性完成,且充填料浆不发生离析现象。
2) 假设充填挡墙及充填体中未留任何孔隙,且这2种介质均表现为完全弹性。
3) 微小位移变形。充填挡墙及充填体受力之后,各点位移均远远小于物体原来尺寸。
钢混充填挡墙施工时,先将一定数量一定规格的钢筋提前插入到周边围岩中,然后喷射混凝土。但在实际工程中,由于岩石强度较低、施工困难或为了满足滤水要求等,导致充填挡墙竖向配筋很难插入到顶部围岩中,因此,在满足上述假设条件下,将充填挡墙视为边界条件为三边简支一边固支的弹性矩形薄板,如图1所示。以充填挡墙高度为方向,充填挡墙宽度为方向建立计算坐标系。设充填挡墙高度为,充填挡墙宽度为,充填挡墙厚度为,一次充填高度为,充填挡墙混凝土极限抗拉强度为s,充填体对充填挡墙的作用荷载为。
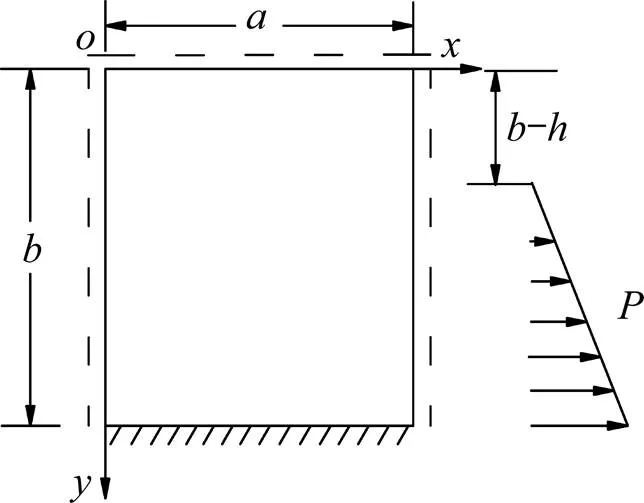
图1 充填挡墙力学模型
根据弹性基础上的薄板理论,在充填体作用下,充填挡墙产生的位移(挠度)()满足:
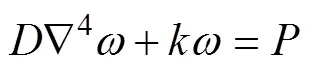
利用式(1)求解出(),根据圣维南原理计算充填挡墙的弯矩和水平应力,弯矩的表达式为
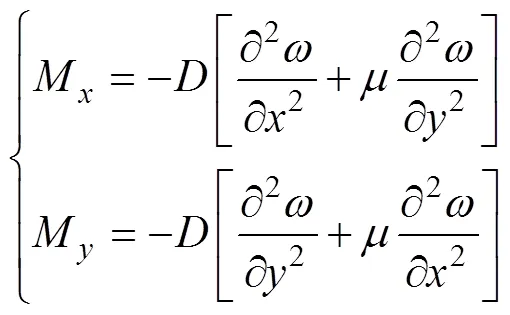
水平应力的表达式为
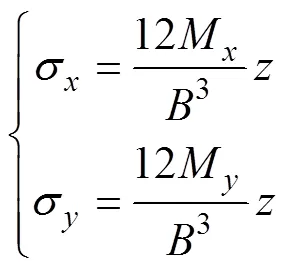
利用式(2)求解出充填挡墙弯矩,通过理论分析确定出充填挡墙的最大弯矩和极限水平应力,利用式(3)求解出充填挡墙厚度。
2 工程实例
金川二矿区具有矿体厚大、破碎、采矿效率高、对破碎矿体适应性好等特点,采用空心砖砌筑挡墙,存在施工效率低、作业周期长的问题,拟采用喷浆式钢筋混凝土充填挡墙。以金川二矿区某巷道处的钢筋混凝土充填挡墙为例,采用土力学的理论确定充填挡墙作用荷载与一次充填高度的关系,为分析充填挡墙厚度与一次充填高度和充填挡墙混凝土抗拉强度的定量关系提供参考。
2.1 充填挡墙作用荷载与一次充填高度的关系
充填料浆充填矿房一般分层进行,若一层一次充填至充填挡墙的顶部,则充填料浆对充填挡墙作用最大。根据充填料浆的形态不同,分成静液态二相流、无黏性松散充填体和黏性松散充填体3种作用形式,经分析可知无黏性松散充填体作用于充填挡墙时,充填料浆对充填挡墙的作用最大[1]。充填料浆作用于充填挡墙时受力分析如图2所示。
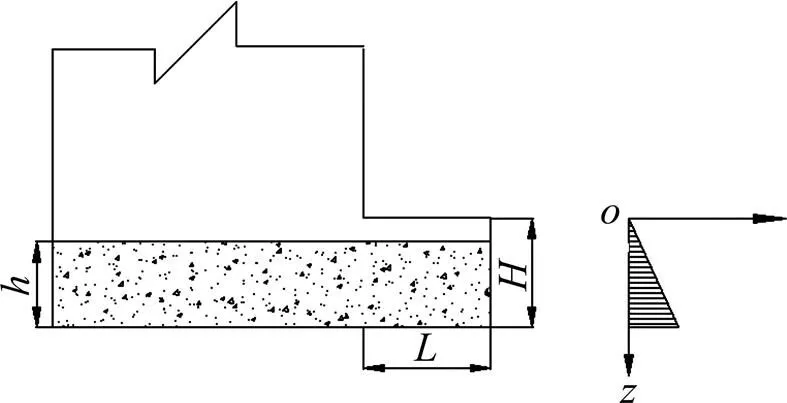
图2 充填料浆低于充填挡墙高度时受力分析
受力计算公式为
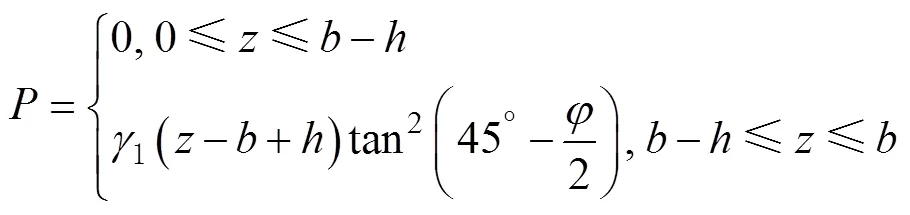
式中:为充填挡墙的高度,m;1为充填料浆容重,kN/m3;为充填料浆的内摩擦角,(°)。
观察式(4)可知,充填体作用于充填挡墙的荷载随着一次充填高度的增大不断增加,呈线性关系。
2.2 基于弹性薄板理论的充填挡墙厚度计算
根据钢混充填挡墙力学模型可知,充填挡墙为三边简支一边固支的弹性矩形薄板,从安全性角度考虑,假定充填挡墙在破坏前的边界条件为四边简支。如图3所示。

图3 四边简支充填挡墙力学模型
边界条件为:
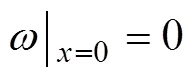
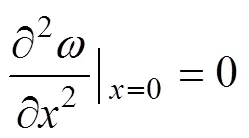
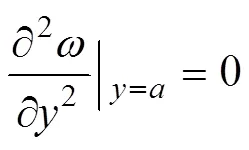
利用纳维解法进行充填挡墙的强度分析,挠度的表达式为
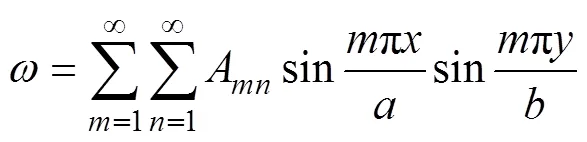
其中,为挡墙长度;和均为任意正整数。显然上述的边界条件都能满足要求。将式(6)代入式(1),得到
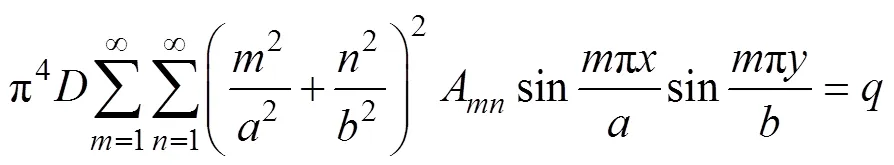
求解系数A,将式(7)右侧的站位有左侧同样的重三角数,即

利用三角函数的正交性:
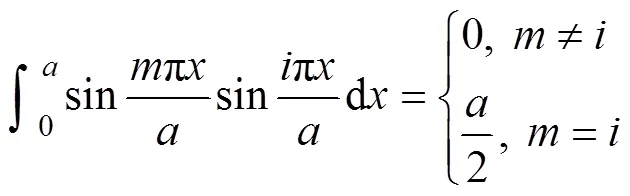
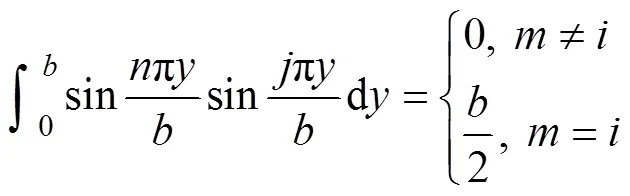
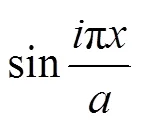
解出C,并代入式(8),得到的展开式为
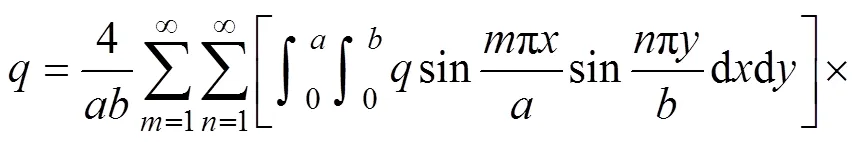
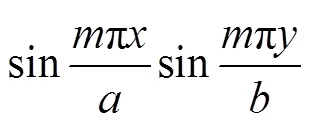
与式(7)对比,得
首先,高中化学教职人员必须要准确有效地了解每一位学生的实际学习情况,然后依照学生的综合素质对其进行准确的划分,同时在对学生进行层次划分的过程当中,必须要时刻关注学生的心理变化情况,准确地告知学生将其进行小组划分对于学生自身化学水平提升的重要性。
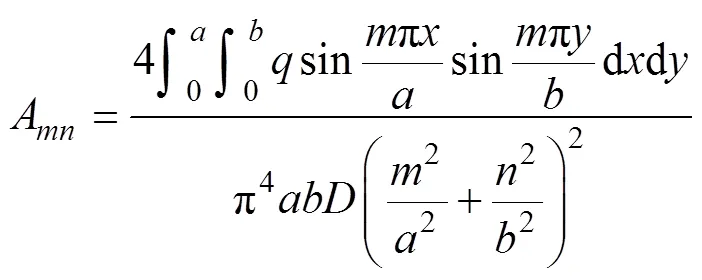
将式(4)代入到式(10)中,对式(10)进行积分,积分式为
代入式(10)可得:

将式(11)代入式(6),可得挠度的表达式为
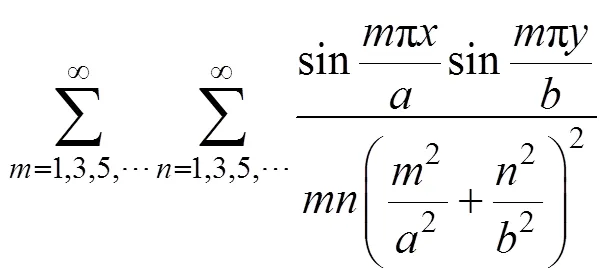

将式(12)代入式(2)得到充填挡墙的弯矩表达式为

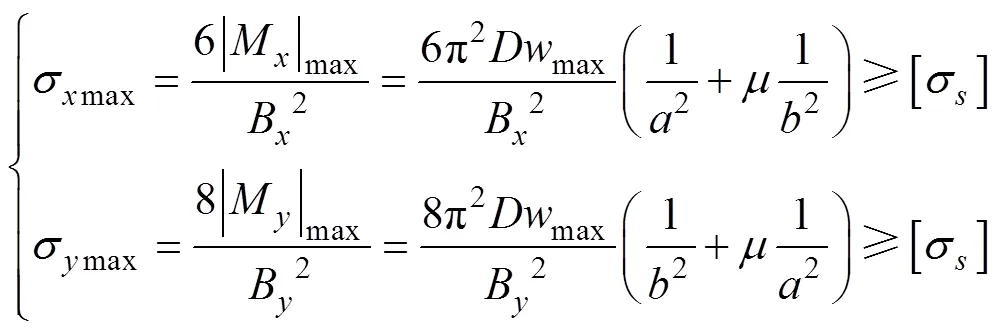
若按照最不利情况考虑,则式(15)的水平应力等于充填挡墙的极限抗拉强度,则式(15)变为
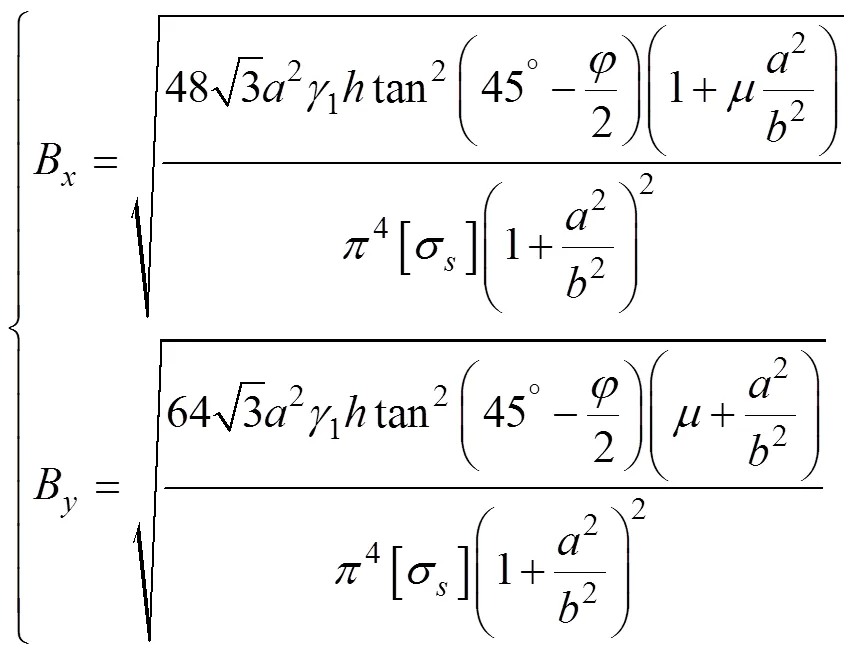
观察式(16)可以发现,在充填挡墙使用位置一定的前提下,充填挡墙厚度与充填挡墙尺寸的变化无关,若充填料浆的物理力学参数不变,充填挡墙的厚度取决于一次充填高度和充填挡墙的抗拉强度,式(16)可以简化为:
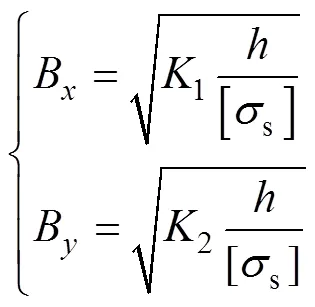
其中:
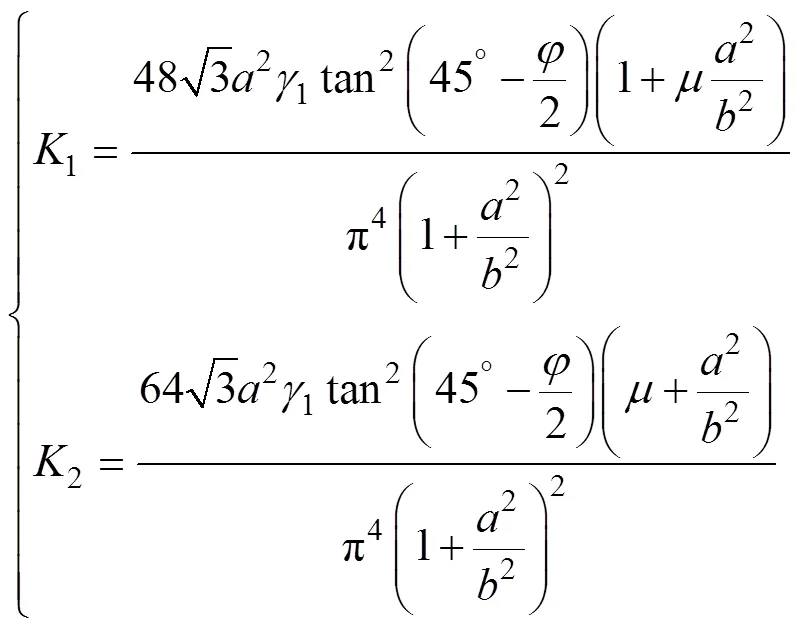
充填挡墙高度为4 m、宽度为5 m,充填体的物理力学参数为1=21 kN/m3,33°,充填挡墙混凝土的泊松比为0.2,施工现场制作充填挡墙多采用C20,C25和C30 3个水平的混凝土,参考GB 50010—2010“钢筋混凝土结构设计规范”[19]可知对应的极限抗拉强度分别为1.1,1.27和1.43 MPa,根据工程经验选择充填体一次充填高度分别为1.0,1.5,2.0,2.5,3.0,3.5和4.0 m 7个水平划分,进行充填挡墙厚度求解,计算结果如图4所示。
由图4可知,无论充填挡墙抗拉强度如何取值,方向上的充填挡墙厚度都比方向上的大,因此,为了满足矿山安全性的要求,应选取较大的值作为充填挡墙的厚度。
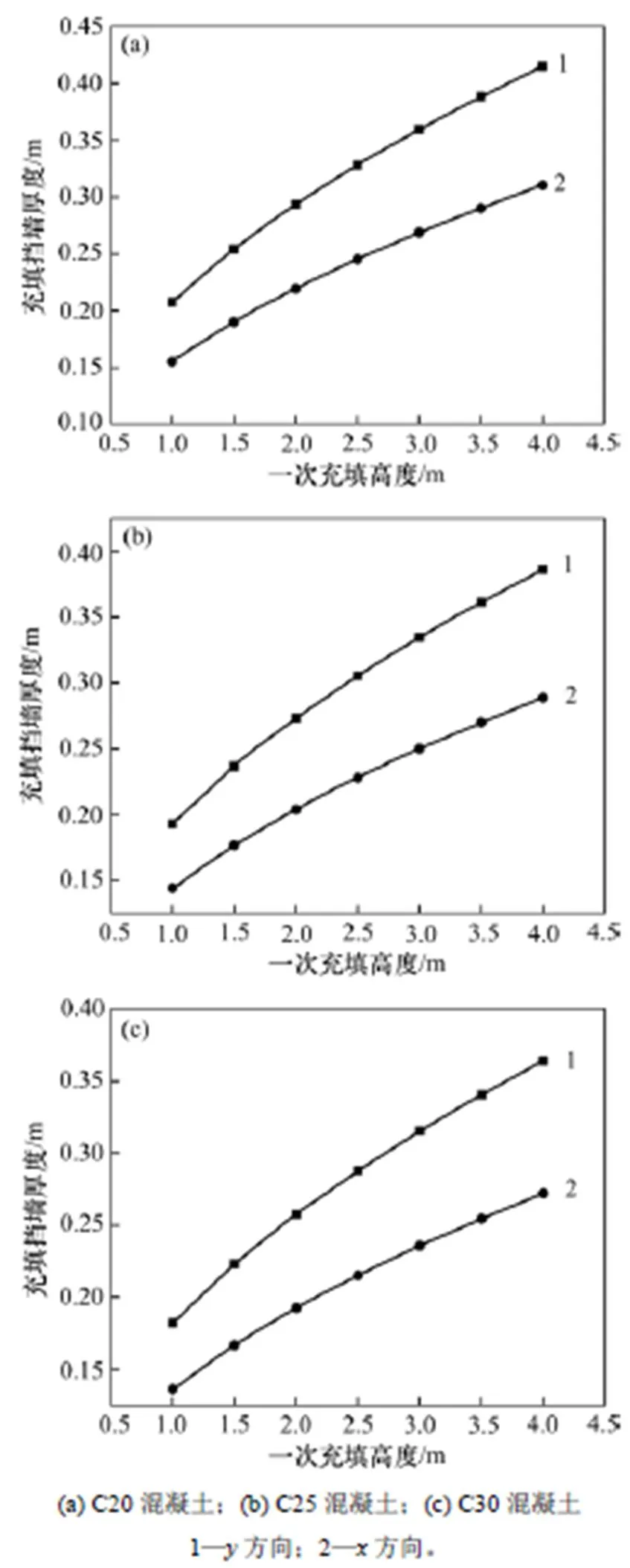
图4 不同方向的一次充填高度与充填挡墙厚度的关系
为了分析不同等级混凝土条件下一次充填高度与充填挡墙厚度的关系,以方向上对应的充填挡墙厚度为例进行说明。不同等级混凝土一次充填高度与充填挡墙厚度的关系如图5所示。

图5 不同等级混凝土的一次充填高度与充填挡墙厚度的关系
由图5可知:C20混凝土在一次充填高度4 m时充填挡墙厚度最大,为416 mm,C30混凝土在一次充填高度4 m时充填挡墙厚度最小,为272 mm,表明相同一次充填高度时,充填挡墙混凝土的抗拉强度越大,对应的充填挡墙厚度越小。
2.3 结果比较
从充填挡墙抗压强度考虑,充填挡墙厚度理论计算公式[13−15]为
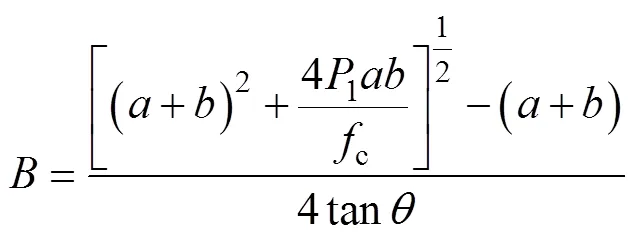
从挡墙抗剪强度考虑,充填挡墙厚度理论计算公式为

从挡墙抗渗性考虑,充填挡墙厚度理论计算公 式为
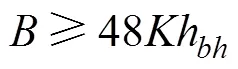
式中:ƒv为挡墙混凝土抗剪强度,MPa;ƒc为挡墙混凝土抗压强度,MPa;1为静水压力荷载,MPa;为充填挡墙嵌入巷道角度,岩石坚固性系数:当<6时,取20°,当>6时,取30°;为挡墙的抗渗性要求,查表取=0.000 03;h为承受静水压头设计高度,m。
现场充填挡墙长度=5 m,假定一次充填高度与充填挡墙高度相同,均为4 m,当现场选用C25混凝土时,参考GB 50010—2010“钢筋混凝土结构设计规范”[19]可知充填挡墙混凝土的抗压强度为11.9 MPa,抗剪强度为1.8 MPa,岩石坚固性系数>6,作用于充填挡墙上静水压力荷载1为0.6 MPa,代入式(19)~(21)计算挡墙厚度,3个公式计算结果分别为95,369和17 mm,选取最大值作为充填挡墙厚度=369 mm。由于现场情况更为复杂,加上施工条件限制,因而现场充填挡墙厚度不能小于理论值,而是应比理论值大10%左右[14],因此,现场施工充填挡墙厚度为400 mm。
充填体的物理力学参数为1=21 kN/m3,33°,充填挡墙混凝土的泊松比=0.2,代入本文得出的式(17),充填挡墙厚度的计算结果分别为289 mm和 386 mm。为了满足充填挡墙安全性和施工的要求,选取充填挡墙厚度=400 mm。
已有充填挡墙厚度理论是将充填挡墙按照四边固定的防水闸门进行设计,充填挡墙承受的荷载按照静水压力计算,经过大量的工程实践验证,该理论计算结果可以满足充填挡墙安全性的要求。本文的理论是将充填挡墙设定为四边简支的弹性薄板,真实地反映了充填体对充填挡墙的作用荷载,且计算结果与已有充填挡墙厚度理论结果相同,同样可以满足充填挡墙安全性的要求,验证了基于弹性薄板理论建立充填挡墙厚度力学模型是正确性和合理性。
综上所述,2种计算充填挡墙厚度理论计算结果相同,都符合工程实际的要求。但本文推导得出的公式充分考虑了充填体对充填挡墙的作用,更加符合工程实际情况,且本文推导出的公式在形式上较简单,因此,对于工程实际具有一定的应用意义。
3 结论
1) 基于弹性薄板理论,选取一次充填高度和充填挡墙混凝土抗拉强度作为充填挡墙厚度的影响因素,建立钢混充填挡墙厚度力学模型,采用纳维解法进行理论分析,推导得出充填挡厚度与一次充填高度和充填挡墙混凝土抗拉强度之间的关系式。
2) 在充填挡墙尺寸和充填料浆物理力学参数一定的前提下,当一次充填高度不变时,充填挡墙的厚度随着混凝土抗拉强度的增大逐渐减小,呈1/2幂次关系;当混凝土抗拉强度不变时,充填挡墙的厚度随着一次充填高度的增加逐渐增大,呈1/2幂次关系。
3) 以金川二矿区某钢混充填挡墙为工程实例,利用本文推导得出的理论公式计算出充填挡墙厚度为400 mm,计算结果与已有充填挡墙理论计算结果相同,验证了充填挡墙厚度力学模型的正确性和合理性。工程中只需要确定充填挡墙的设计尺寸、充填体的物理力学参数、一次充填高度和混凝土抗拉强度,就可利用推导出的公式确定出充填挡墙的厚度,具有一定的工程实用意义。
[1] 黄建君. 充填法挡墙强度模型研究及应用[D]. 昆明: 昆明理工大学国土资源工程学院, 2014: 21−28. HUANG Jianjun. Research and application of filling method of retaining wall strength mode[D]. Kunming University of Science and Technology. College of L and and Resources, 2014: 21−28.
[2] 郑学敏. 大型采空区井下密闭墙设计[J]. 金属矿山, 2002, 12(12): 56−57. ZHENG Xuemin. Large underground goaf seal design[J]. Metal Mine, 2002, 12(12): 56−57.
[3] YU Guangyun, BAI Yongsheng, SHENG Ping, et al. Mechanical performance of a double-face reinforced retaining wall in an area disturbed by mining[J]. Mining Science and Technology, 2009(19): 36−39.
[4] TAN Y L, YU F H, NING J G, et al. Design and construction of entry retaining wall along a gob side under hard roof stratum[J]. International Journal of Rock Mechanics & Mining Sciences, 2015(77): 115−121.
[5] ZHOU Baojing, XU Jinhai, ZHAO Maosen, et al. Stability study on naturally filling body in gob-side entry retaining[J]. International Journal of Mining Science and Technology, 2012(22): 423−427.
[6] 张葆春, 曹宗权, 赵永和, 等. 尾砂胶结充填挡墙受力分析及工程应用[J]. 有色金属科学与工程, 2011, 2(5): 57−60. ZHANG Baochun, CAO Zongquan, ZHAO Yonghe, et al. Bulkhead stress analysis in filling cemented tailings and its practical application[J]. Nonferrous Metals Science and Engineering, 2011, 2(5): 57−60.
[7] 张海波, 刘芳芳. 充填采矿法充填挡墙合理结构参数研究及应用[J]. 化工矿物与加工, 2014(5): 33−35. ZHANG Haibo, LIU Fangfang. Research and application of reasonable structural parameters for filling retaining wall in cut-and-fill mining method[J]. Mineral and Chemical Processing, 2014(5): 33−35.
[8] 采矿设计手册编委会. 采矿设计手册(井巷工程卷)[M]. 北京: 中国建筑工业出版社, 1988: 763−766. Editorial Board of the Mining Design Manual. Mining design handbook (well and alley engineering roll)[M]. Beijing: China Construction Industry Press, 1988: 763−766.
[9] HELINSKI M, FAHEY M, FOURIE A. Behavior of cemented paste backfill in two mine stopes: measurements and modeling[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011(2): 171−182.
[10] STREUDERS S B. Rock engineering related experiences with the use of backfill on the deepest platinum mine[C]// Minefill 2011, 10th International Symposium on Mining with Backfill. Cape Town: The Southern African Institute of Mining and Metallurgy, 2011: 49−64.
[11] JOUGHIN W C, BESTER.M W M. PLOOY D U. Mining methods and backfill at South Deep Gold Mine[C]// Minefill 2011, 10th International Symposium on Mining with Backfill. The Southern African Institute of Mining and Metallurgy, Cape Town: 2011: 69−78.
[12] DUTTA S, GRICE T. Mining with backfill at Rajpura Dariba Mine[C]// Minefill 2011, 10th International Symposium on Mining with Backfill. Cape Town: The Southern African Institute of Mining and Metallurgy, 2011: 87−98.
[13] 王丽红, 李夕兵, 赵国彦, 等. 永平铜矿充填挡墙安全设计及工程应用[J]. 矿冶工程, 2013, 12(6): 6−12. WANG Lihong, LI Xibing, ZHAO Guoyan, et al. Safety design of backfilled retaining wall and its application in Yongping Copper Mine[J]. Mining and Metallurgical Engineering, 2013, 12(6): 6−12.
[14] 汪海萍, 宋卫东, 张兴才, 等. 大冶铁矿浅孔留矿嗣后胶结充填挡墙设计[J]. 有色金属, 2014, 9(5): 14−26. WANG Haiping, SONG Weidong, ZHANG Xingcai, et al. Design for retaining wall of short-hole shrinkage subsequent cemented filling method in Daye Iron Mine[J]. Nonferrous Metals, 2014, 9(5): 14−26.
[15] 袁世伦. 盘区大孔采矿采场全尾砂充填挡墙力学特性研究[J]. 中国矿山工程, 2011, 8(4): 9−12. YUAN Shilun. Study on mechanical property of whole tailing filling retaining wall in panel large hole mining stope[J]. China Mine Engineering, 2011, 8(4): 9−12.
[16] NORTJÉ A S, MEINTJIES H A C, JOUGHIN W C. Design of hydraulic backfill bulkheads at south deep gold mine[R]. Montreal: Euler De Souza Publications, 2007: 1−11.
[17] KANOWNA B, OPERATION R. Assessment of 12 hour fibrecrete curing on Raleigh paste bulkheads[R]. Victoria: Revell Resources Pty Ltd Atf Revell Family Trust, 2010: 1−12.
[18] 徐芝纶. 弹性力学[M]. 4版. 北京: 高等教育出版社, 2006. XU Zhilun. Elasticity[M]. 4th ed. Beijing: Higher Education Press, 2006.
[19] GB 50010—2010,混凝土结构设计规范[S]. GB 50010—2010, Code for design of concrete structures[S].
(编辑 赵俊)
New model of filling-retaining wall thickness based on theory of elastic plates
ZHANG Aiqing1, WU Aixiang1, HAN Bin1, WANG Yiming1, CHANG Baomeng1, WANG Hu1, 2, WU Shuanjun1,2
(1. School of Civil & Resources Engineering, University of Science & Technology Beijing, Beijing 100083, China; 2. Jinchuan Group Co. Ltd., Jinchang 737100, China)
In order to calculate the thickness of filling-retaining wall correctly, the height of once-filling and concrete tensile strength were chosen as factors. Based on theory of elastic plates, the mechanical model was built for thickness of filling-retaining wall reinforced, and the relationship between filling height, concrete tensile strength and thickness of retaining wall was deduced. Taking Jinchuan NO.2 mine as the example for engineering analysis, the rule of filling height, concrete tensile strength and thickness of retaining wall was studied by CVM. The result shows that the thickness of filling decreases with the increase of the concrete tensile strength, and shows 1/2 power relations with certain retaining wall size and physical and mechanical parameters of filling slurry. And the thickness of filling increases with the increase of the height of once-filling, and shows 1/2 power relations under constant concrete tensile strength. Comparing the results with the existing theory of filling-retaining wall thickness, the correctness and rationality of the mechanical model are verified.
filling- retaining wall; mechanical model; theory of elastic plates; variation law
TD853, TU375
A
10.11817/j.issn.1672-7207.2018.03.024
1672−7207(2018)03−0696−07
2017−03−12;
2017−06−20
新世纪优秀人才支持计划项目(NCET-13-0669) (Project(NCET-13-0669) supported by Program for New Century Excellent Talents in University)
吴爱祥,博士,教授,从事矿山岩石力学和溶浸采矿等研究;E-mail: wuaixiang@126.com
