基于批次回归系数的热轧带钢头部拉窄过程监控与诊断

孙勇，何飞，杨德斌



基于批次回归系数的热轧带钢头部拉窄过程监控与诊断

孙勇1, 2，何飞1，杨德斌2

(1. 北京科技大学 钢铁共性技术协同创新中心，北京，100083； 2. 北京科技大学 机械工程学院，北京，100083)

针对目前热轧带钢生产过程数据分析主要利用工艺参数和产品质量的平均值，忽略带钢长度方向上的变异信息，提出一种新的三维生产过程数据的监控框架。首先建立热连轧机组精轧过程中每块带钢的工艺变量与宽度间的偏最小二乘模型，获得所有批次的回归系数并组成二维数据矩阵，利用回归系数矩阵建立主成分分析模型进行监控和诊断。研究结果表明：该方法可以有效获取过程变量对质量的影响关系、实现过程监控，并有效给出质量异常的原因。

批次数据分析；偏最小二乘回归；回归系数；过程监控；质量诊断

热连轧带钢生产以连铸板坯为原料，将钢材加工成厚度为2~6 mm的板带产品。常用的带钢热连轧生产线一般包括加热炉区、粗轧区、粗精轧之间的中间辊道及飞剪、精轧区、热输出辊道及层流冷却装置、卷取区等[1]。宽度精度是热轧产品重要的质量参数[2]，头部拉窄是指带钢头部的实际宽度小于目标宽度，造成产品质量不合格，给企业带来重大经济损失。在热轧带钢生产过程中，每卷带钢会生成实时的工艺参数与产品质量表，实际的多卷带钢生产会得到生产过程的三维批次数据(批次×时间×工艺变量)。如何充分利用三维批次数据对生产过程进行监控及当出现质量异常时，如何利用数据分析方法进行批次生产过程的诊断等，是有待解决的难题。传统的主成分分析(principal component analysis，PCA)、偏最小二乘(partial least-squares, PLS)等多元统计方法都是针对二维数据矩阵进行分析，无法直接应用于三维批次数据，因此，一些研究者提出了基于矩阵展开的批次数据处理框架，并将其应用于批次生产过程的监控。其方法是将三维批次数据基于批次或者基于变量展开并重组为二维数据后，运用各种传统的多元统计方法对二维数据进行建模、监控和诊断，从而产生一系列处理批次数据的新方法，例如多向PCA[3−4]、多向PLS[5]以及多向独立成分分析[6]等。针对批次生产过程中变量间存在的非线性关系，非线性方法被引入批次生产过程，如多向核PCA[7]、多向核独立成分分析[8]以及分层的核PLS[9]。基于矩阵展开的批次数据处理框架原理简单、易于实现，但是存在明显的缺点，如：基于批次展开的方法需要对各批次长度不等的批次数据进行长度对齐，而长度对齐会改变数据的变异信息，展开后的数据矩阵中变量数可能远大于样本数，不利于回归建模；而基于变量展开的方法是对所有批次所有样本点统一进行标准化，忽略了变量轨迹中的非线性和动态特性[10]，且发现异常样本点后难以解释。这2种展开方法的共同缺点是：将三维矩阵展开成二维矩阵时因破坏数据结构而丢失了一些重要变异信息。一些研究者提出基于三线性的批次数据处理框架如基于并行因子模型和Tucker模型的方法[11−12]。其方法是直接将三维数据张量分解成3个方向上的线性成分的外积和，3个方向的负载向量提取了过程变量在对应方向上存在的线性关系。该方法不需要进行矩阵展开，避免了数据结构的破坏，比传统的基于矩阵展开的批次数据处理框架更加稳定，但是其明显的缺点是适应性差、计算复杂以及收敛速度慢，而且难以对载荷向量和残差进行统计检验。在热轧带钢生产过程中，因难以使用上述三维批次处理方法，目前常用方法是计算每个批次内样本数据中每个变量的均值，获得二维矩阵(批次×工艺变量)，进而在二维矩阵的基础上进行简单过程能力评价或多元统计过程监控。其缺点是忽略了带钢长度方向上的变异信息。为此，本文提出一种新的批次数据处理框架，在计算批次工艺过程数据和批次质量数据之间的偏最小二乘回归系数(批次×工艺变量)后，在回归系数的基础上建立主成分分析模型进行过程监控和质量诊断，不需要进行各批次间的长度对齐，避免了对数据结构的破坏，简化了计算，既考虑了工艺数据与质量数据的相关性，又考虑了带钢长度方向上的变异信息。

1 偏最小二乘回归

偏最小二乘回归分析在提取自工艺变量成分时考虑了工艺变量与质量变量的协方差最大化，在消除原有工艺变量间多重相关性的同时，还充分反映了工艺变量与质量变量间的相关关系。具体计算步骤如下。

2) 应用 NIPALS 算法[13]计算的得分向量、载荷向量和由计算的权重向量。分别从和中减去潜变量，得到退化的和：

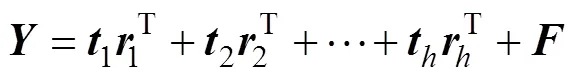
其中：为残差矩阵。

5) 最后计算回归的复测定系数：

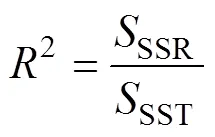
2 主成分监控与诊断

因生产过程工艺变量众多，而且变量间存在相关影响关系，可采用PCA模型进行生产过程的监控，发现异常点时利用贡献图法实施诊断。算法步骤如下。

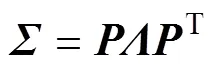
2) 利用Hotelling2和平方预测误差(squared prediction error,SP)对过程性能实施监控。通过监测2和SP否超限，确定过程是否处于正常工况。

3) 发现超限严重的样本点后，查看该样本点的2和SP的贡献图，找出贡献突出的工艺变量，确定为故障变量。

Hotelling2统计量、2的置信限以及基于2的贡献图的计算方法[14]为：

(10)

(12)

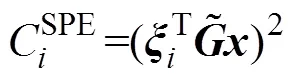
3 批次回归系数分析

针对三维批次数据，本文提出一种基于批次回归系数的多变量统计过程监控框架。首先，利用多元线性回归、PLS或样条回归等方法建立工艺变量与质量变量间的回归模型；其次，在回归系数的基础上建立多变量统计过程监控模型，用2和SP对过程实施监控，发现异常后，利用贡献图法寻找故障变量。其中，PLS既考虑了工艺变量和质量变量的变异性，又考虑了工艺变量对质量变量的影响关系。在热轧带钢生产过程中，样本数据包含多个变量且变量间存在相关性，因此，首先利用PLS回归获得工艺变量与质量变量间的影响关系；此外，工艺变量众多，而且回归系数间存在互相影响，使用单变量效率低且难以提取变量间的相关影响，因此，用多变量统计过程监控方法比孤立地使用单变量统计过程监控方法更加合理。

本文利用偏最小二乘回归系数的主成分分析方法(principal component analysis based on partial least squares regression coefficient, PLSRC-PCA)进行数据分析。首先选择PLS法获得每块带钢的工艺变量与质量变量的回归系数，然后利用PCA方法进行监控，采用贡献图实施诊断，总体流程图见图1，具体步骤如下。

图1 PLSRC-PCA的流程图

4) 故障诊断。若新样本异常，则利用式(10)和(13)计算各工艺变量的贡献值，从而诊断出引起新样本异常的故障变量。

4 实验与结果分析

本文利用仿真数据验证PLSRC-PCA方法的有效性，利用该方法对热轧带钢头部拉窄数据建立监控模型，实现过程监控和质量诊断，并与基于多元线性回归系数的主成分分析监控模型(principal component analysis based on multivariate linear regression coefficient, MLRC-PCA)、基于均值的主成分分析监控模型(principal component analysis based on mean value, mean-PCA)、基于均值的偏最小二乘监控模型(partial least squares based on mean value, mean-PLS)进行 对比。

4.1 仿真实验

仿真案例中设置的工艺变量矩阵(300×101×3)中包含3个变量1，2和3，质量变量矩阵(300×101×1)中包含1个变量，均包含300个批次，每批次有101个时间点。正常的批次数据设计如下：

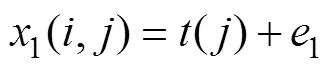
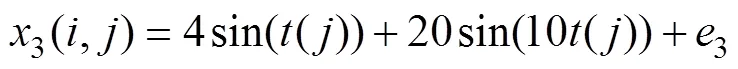
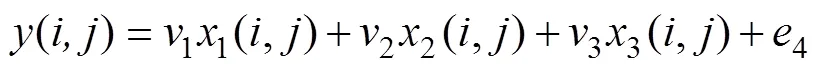
在3上增加异常，具体的异常批次数据设计如下：

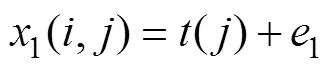
本文在仿真案例部分主要对比PLSRC-PCA方法与以下3种方法的检测结果。

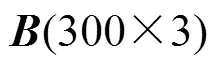
4种监控模型的检测结果如表1所示。通过对比这4种监控模型的误报率和漏检率发现：MLRC-PCA方法和PLSRC-PCA方法的误报率和漏检率明显比mean-PCA方法和mean-PLS方法的低，说明基于批次回归系数的PCA监控模型方法在监控三维批次生产数据时更有优势。PLSRC-PCA方法监控图如图3所示。用贡献图对超限批次进行故障诊断，故障变量指向变量3，与预设故障一致，验证了PLSRC-PCA方法在监控三维批次生产数据的有效性。

4.2 热轧带钢头部拉窄数据的PLSRC-PCA监控与诊断

头部拉窄数据包含3个方向的维度(批次×时 间×工艺变量)。在变量方向，有1个质量变量和56个工艺变量，变量信息如表2所示。

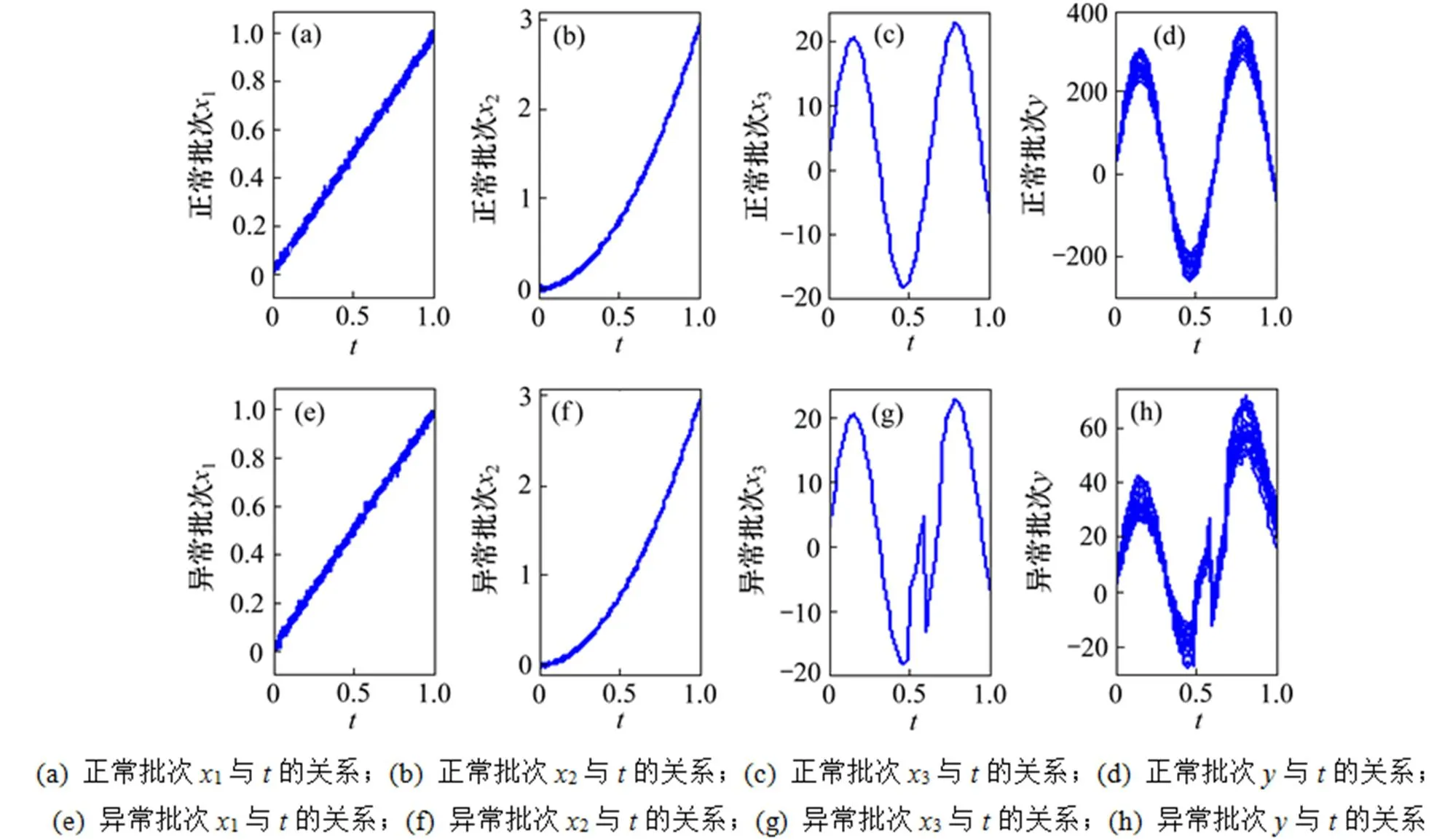
图2 仿真数据的前20个批次的原始轨迹图

表1 4种监控模型的检测结果

在批次方向，以1卷钢为1个批次，共采集182个正常批次和115个异常批次，共297个批次。样本的采样间隔为1 ms，每个批次采集的样本数不同。

4.2.1 数据预处理

由于各变量采集点分布在热轧生产线的不同位置，在热轧生产过程中，钢板依次进入各轧机，造成各变量开始测量和结束测量的时间不同，同一时刻各变量采集的数据所对应的钢板位置不同，而且钢板由厚变薄，在不同工序停留的时间长度也不同。使用数据统计方法进行过程监控与诊断时要求：各工艺变量间、工艺变量与质量变量间要对应钢板的同一位置，即每一个采样点都是由钢板相同位置的工艺参数和质量参数组成。考虑生产钢板中各处速度以及各轧机前后滑因子等因素，实现每个批次内各变量的样本点一一对应。

图3 仿真数据的PLS-RCPCA模型的监控图

表2 热轧带钢头部拉窄数据分析变量

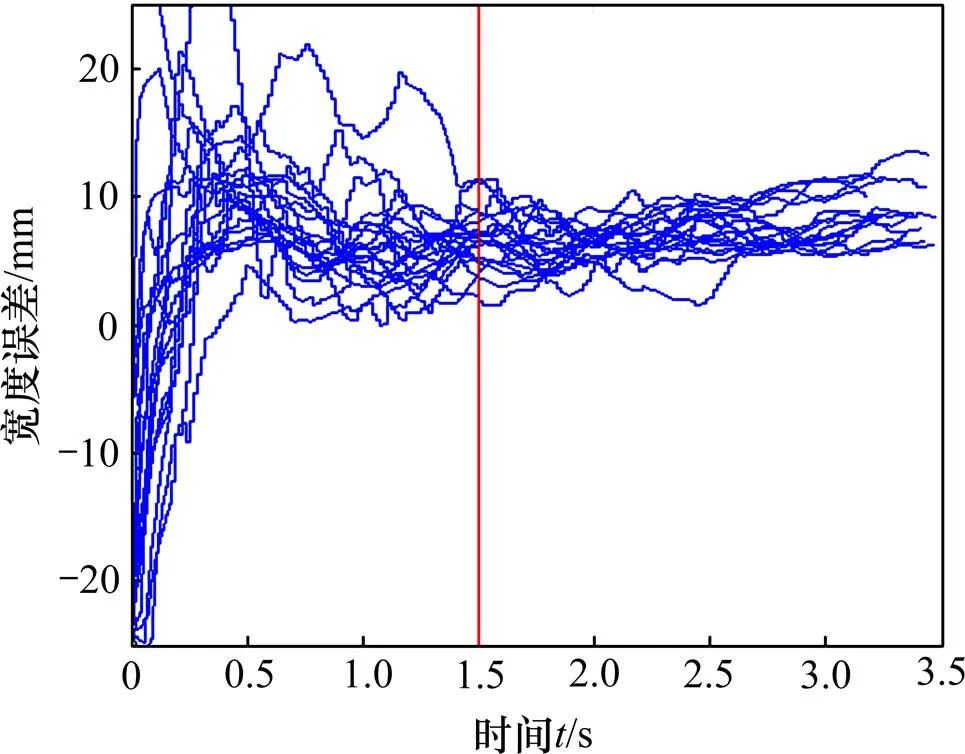
图4 前20个批次的宽度误差的曲线

4.2.2 PLS回归

4.2.3 过程监控

将1中的132个批次回归系数确定为训练集，将1中另外50个批次回归系数和2中114个批次回归系数作为测试集，建立基于PLS回归系数的PCA模型，计算训练集2和SP的控制限以及测试集2和SP，实现对批次生产过程的监控。测试集的监控如图5所示。建立头部拉窄数据的mean-PCA模型、mean-PLS模型和MLRC-PCA模型，具体步骤见4.1节，4种监控模型的检测结果如表3所示。

通过对比4种监控模型的误报率和漏检率发现：MLRC-PCA方法和PLSRC-PCA方法的误报率和漏检率明显比mean-PCA方法的低，说明基于批次回归系数的PCA监控模型方法在监控头部拉窄数据时更有优势。而在4种模型中，mean-PCA方法的2漏检率和SP漏检率都很高，即使诊断出故障变量，可靠性也不强。与MLRC-PCA方法相比，PLSRC-PCA方法具有更低的SP误报率和2漏检率，占有较强的优势。

4.2.4 故障诊断

对检测到的严重超限的几个批次进行故障诊断，观察它们的贡献图，确定贡献较大的变量，寻找引起样本异常的原因。由图6可知：T中严重超限的批次有第85，104，132和157批次，SP中严重超限的批次有第85，104，124和132批次。

由图6所示为第85批次的T的贡献图。由图6可诊断出故障变量可能是活套5套量(变量15)和活套5高度(变量55)。PLSRC-PCA中的所有严重超限批次的诊断结果如表4所示。

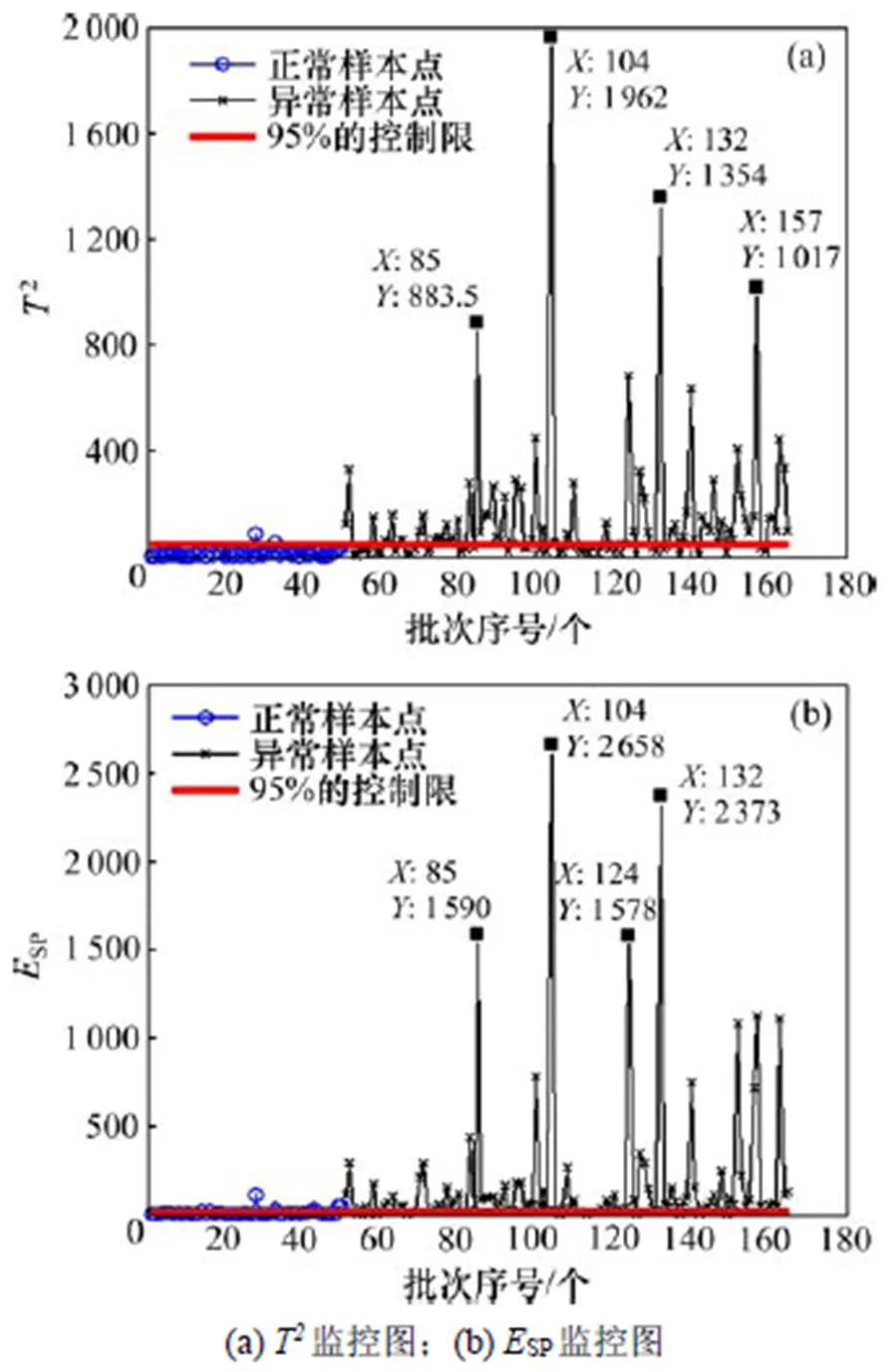
图5 头部拉窄数据的PLS-RCPCA模型的监控图

表3 4种监控模型的检测结果

图6 PLS-RCPCA模型第85批次的T2贡献图

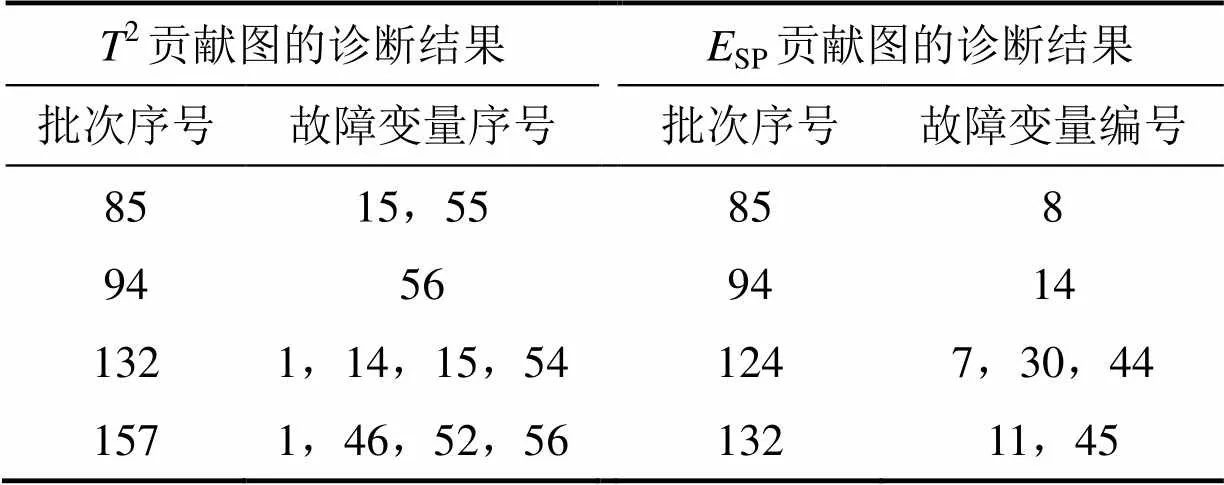
表4 PLSRC-PCA监控模型所有严重超限批次的诊断结果

综合上述各批次的诊断结果，根据出现频次可以初步确定导致热轧带钢头部拉窄的主要故障变量为精轧入口温度(变量1)、活套4的套量(变量14)、活套5的套量(变量15)、活套6的高度(变量56)，它们是故障排查的重点环节。

在实际生产中对结果进行验证，精轧入口温度的控制异常给后续加工带来了影响，而且由于前3机架驱动电机有减速器，而后4个机架没有减速器，导致前3个机架和后4个机架的电机控制特性不同，后3个活套的套量和活套高度控制不协调等。

5 结论

1) 由PLSRC-PCA监控模型所得结果优于由mean-PCA，mean-PLS和MLRC-PCA这3种监控模型所得结果。如在热轧带钢头部拉窄数据分析中，与mean-PLS监控模型相比，PLSRC-PCA监控模型的2误报率从40%下降到4%，2漏检率从40%下降到38%，而SP误报率从62%下降到22%，SP漏检率从43%下降到17%。

2) 针对头部拉窄数据，PLSRC-PCA方法诊断出的故障变量为精轧入口温度、活套4和5的套量、活套6的高度。在生产过程中，应重视过程变量的监控，及时发现异常工艺。此外，回归系数的计算可以推广到非线性回归，而且可以应用于冶金领域其他过程或者其他领域。

[1] 何飞, 徐金梧, 梁治国, 等. 基于核熵成分分析的热轧带钢自适应聚类分析[J]. 中南大学学报(自然科学版), 2012, 43(5): 1732−1738. HE Fei, XU Jinwu, LIANG Zhiguo, et al. Hot rolled strip state clustering based on kernel entropy component analysis[J]. Journal of Central South University(Science and Technology), 2012, 43(5): 1732−1738.

[2] 董永刚, 张文志, 宋剑锋. 钢轨万能轧制过程轨底宽展的理论及实验研究[J]. 中南大学学报(自然科学版), 2011, 42(9): 2076−2080.DONG Yonggang, ZHANG Wenzhi, SONG Jianfeng. Theoretical and experimental research on spread of base of rail in universal rolling[J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2076−2080.

[3] 郭金玉, 王纲. 非线性多尺度多向主元分析方法[J]. 中南大学学报(自然科学版), 2003, 34(Z1): 82−84. GUO Jinyu, WANG Gang. Nonlinear multiscale multiway principal component analysis[J]. Journal of Central South University(Science and Technology), 2003, 34(Z1): 82−84.

[4] PENG Jianxin, LIU Haiou, HU Yuhui, et al. ASCS online fault detection and isolation based on an improved MPCA[J]. Chinese Journal of Mechanical Engineering, 2014, 27(5):1047−1056.

[5] CALIMAG-WILLIAMS K, KNOBEL G, GOICOECHEA H C, et al. Achieving second order advantage with multi-way partial least squares and residual bi-linearization with total synchronous fluorescence data of monohydroxy-polycyclic aromatic hydrocarbons in urine samples[J]. Analytica Chimica Acta, 2014, 811: 60−69.

[6] YU Jie, CHEN Jingyan, RASHID M M. Multiway independent component analysis mixture model and mutual information based fault detection and diagnosis approach of multiphase batch processes[J]. AICHE Journal, 2013, 59(8): 2761−2779.

[7] WANG Yanjun, JIA Mingxing, MAO Zhizhong. Weak fault monitoring method for batch process based on multi-model SDKPCA[J]. Chemometrics and Intelligent Laboratory Systems, 2012, 118(4): 1−12.

[8] RASHID M M, YU Jie. Nonlinear and non-Gaussian dynamic batch process monitoring using a new multiway kernel independent component analysis and multidimensional mutual information based dissimilarity approach[J]. Industrial & Engineering Chemistry Research, 2012, 51(33): 10910−10920.

[9] ZHANG Yingwei, HU Zhizhong. On-line batch process monitoring using hierarchical kernel partial least squares[J]. Chemical Engineering Research and Design, 2011, 89(10): 2078−2084.

[10] WESTERHUIS J A, KOURTI T, MACGREGOR J F. Comparing alternative approaches for multivariate statistical analysis of batch process data[J]. Journal of Chemometrics, 1999, 13(3/4): 397−413.

[11] LOUWERSE D J, SMILDE A K. Multivariate statistical process control of batch processes based on three-way models[J]. Chemical Engineering Science, 2000, 55(7): 1225−1235.

[12] YU Huarong, QU Fangshu, LIANG Heng, et al. Understanding ultrafiltration membrane fouling by extracellular organic matter of microcystis aeruginosa using fluorescence excitation- emission matrix coupled with parallel factor analysis[J]. Desalination, 2014, 337: 67−75.

[13] 王惠文, 吴载兵, 孟洁. 偏最小二乘回归的线性与非线性方法[M]. 北京: 国防工业出版社, 2006: 97−104.WANG Huiwen, WU Zaibing, MENG Jie. Partial least squares regression-linear and nonlinear methods[M]. Beijing: National Defend Industry Press, 2006: 97−104.

[14] 周东华, 李钢, 李元. 数据驱动的工业过程故障诊断技术:基于主元分析和偏最小二乘的方法[M]. 北京: 科学出版社, 2011: 25−29.ZHOU Donghua, LI Gang, LI Yuan. Data-driven industrial process fault diagnosis technology: based on principal component analysis and partial least squaresmethod[M]. Beijing: Science Press, 2011: 25−29.

[15] 北京科技大学. 一种热连轧工艺过程采集数据同步化方法: 中国, CN102323794B[P]. 2012−01−18.University of Science & Technology Beijing. Method for synchronizing data acquired in hot continuous rolling process: China. CN102323794B[P]. 2012−01−18.

(编辑 陈灿华)

Process monitoring and diagnosis of head width narrowing of hot rolled strip based on regression coefficients of different batches

SUN Yong1, 2, HE Fei1, YANG Debin2

(1. Collaborative Innovation Center of Steel Technology, University of Science and Technology Beijing, Beijing 100083, China; 2. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Considering that the current data analysis methods usually use the mean value of process and quality parameters in hot rolled strip production without including the variation information in the longitudinal direction of the strip, a novel framework was introduced for process monitoring using three-way dataset. Firstly, the partial least squares model between process variables and width of each strip after finishing hot rolling was built. And then, a two-way matrix was obtained, which consisted of regression coefficients of all batches. Finally, regression coefficients matrix was used to process monitoring and diagnosis based on principal component analysis. The results show that the new method can not only effectively obtain the relationship between the process and quality parameter, but also finish process monitoring and explain why there appears abnormal quality.

batch data analysis; partial least squares regression; regression coefficients; process monitoring; quality diagnosis

TG335.5

A

10.11817/j.issn.1672-7207.2018.03.009

1672−7207(2018)03−0574−09

2017−03−07；

2017−05−13

国家自然科学基金资助项目(51204018)；国家“十二五”科技支撑计划项目(2015BAF30B01)；北京高等学校青年英才计划项目(YETP0422)；中央高校基本科研业务费资助项目(FRF-BR-16-025A) (Project(51204018) supported by the National Natural Science Foundation of China; Project(2015BAF30B01) supported by the National Key Technology R&D Program of the 12th Five-year Plan of China; Project(YETP0422) supported by the Beijing Youth Talents Program of University; Project(FRF-BR-16-025A) supported by the Fundamental Research Funds for Central Universities)

何飞，博士，副研究员，从事生产过程质量建模、质量在线检测等研究；E-mail: hefei@ustb.edu.com