纯电动车自适应巡航纵向控制方法研究∗
2018-04-11李天骄孙成伟
初 亮,李天骄,孙成伟
前言
自适应巡航系统的纵向控制算法是连接上层自适应巡航决策层算法和下层车辆执行机构的桥梁。接受来自自适应巡航系统决策层算法的期望加速度或减速度信号,并转化为对执行层驱动或制动机构的控制信号,是保证自适应巡航系统实现效果的关键所在。
由于车辆驱动、制动系统十分复杂,有着极强的非线性和耦合性,难以建立数学模型来精确描述。因此国内外学者对于自适应巡航纵向控制算法多基于无模型或少模型控制。文献[1]中利用CarSim与Simulink建立了一种车辆纵向动力学控制模型,并基于最优控制和PID控制设计上下两层的自适应巡航控制系统。文献[2]中应用参数自整定模糊-PID控制,通过模糊规则对PID的3个参数进行调节实现汽车纵向控制。文献[3]中基于模糊逻辑和滑模控制理论设计双层自适应巡航系统,依据车辆传动系统动力学特性确定模糊控制规则并构建了驱动、制动切换逻辑曲线保证系统协调性。
以上文献关于汽车纵向动力学控制方法多基于车辆本体特性整定PID参数或建立模糊控制规则。若外界环境(坡度、风速等)发生变化,将会对车辆加速度控制精度产生较大影响。目前对于传统发动机车辆自适应巡航纵向动力学控制算法研究较多。对于纯电动车纵向动力学控制算法的研究较少。对于纯电动车自适应巡航系统而言,驱动控制机构为电机;考虑到制动能量回收特性,纯电动车制动控制机构包括电机和液压制动系统。相较于传统车,制动控制更为复杂。
本文中首先设计了自适应巡航系统制动过程制动力分配策略,考虑外界环境风速和坡度对控制系统的干扰,建立基于加权最小二乘拟合的模式切换策略,并基于迭代学习算法设计驱动和制动控制方法。基于最优线性二次型设计上层决策算法,并在CarSim和Simulink下联合仿真完成算法验证,并与传统PID控制方法结果进行对比。
1 制动力分配策略
本文中研究的目标车型为前轴驱动的纯电动轿车构型。电机通过主减速器对车轮施加驱动力矩或制动力矩。液压制动力由ESC调节。管路布置按照II型布置。通过控制ESC的阀和液压泵电机电流实现前、后轴轮缸压力的主动控制。
制动力分配包括前、后轴制动力分配和电、液制动力分配。前、后轴制动力分配受到法规的严格限制[4],如图1所示。其中B线规定前轴分配制动力的最大值。C线规定后轴分配制动力的最大值。为充分利用前轴电机制动回收制动能量并考虑整车安全性,基于前期对于制动能量回收系统的研究[5],设计如图2所示制动力分配策略。

图1 法规制动力分配线

图2 制动力分配策略
当制动强度z<z1时,主要由前轴电机施加制动力,液压系统不参与制动;当制动强度z1<z<z2时,达到法规下线,后轴液压参与制动,制动力沿着法规下线分配;当制动强度z2<z<z3时,电机制动力达到最大值,此时增加的制动力由后轴补偿。当z>z3时,为充分利用地面附着条件,制动力分配按照原车B线分配。z1,z2和z3按式(1)[6]计算:

式中:b为质心到后轴距离;L为质心高度;rw为轮胎滚动半径;hg为质心高度;Tm,max为电机最大制动转矩;M为整车整备质量。
2 模式切换策略
由于驱动机构和制动机构为两套不同的系统,二者不能同时工作。因此需要一种模式切换策略确定工作机构。传统方式一般按照期望加速度0为界划分驱动和制动模式。然而该种方法未考虑传动系统阻力及外界阻力的影响。文献[7]中提出了一种滑行试验方法确定模式切换逻辑曲线。取节气门开度为0做滑行试验,标定出不同速度下的最大减速度值,以此确定驱动制动切换的逻辑曲线。然而该种方法未考虑外界环境变化(车速、坡度变化)对切换曲线的影响。本文中采用基于加权最小二乘拟合算法确定模式切换逻辑曲线。
根据车辆驱动力行驶阻力的分析[8],在车辆滑行状态时,其加速度a和速度v存在如下的二次关系式:

由于行驶过程中,车辆受到的坡道阻力和空气阻力会由于道路坡度和风速的变化而变化,因此式中的系数A,B和C数值也会不断变化。本文中采用最小二乘拟合的方法实时辨识关系式参数,对之前观测的车辆速度和加速度数据进行拟合,并预测当前速度下的切换基准加速度。考虑到观测数据的时效性,变化后的环境信息往往蕴含于新观测的数据点中,而与先前观测数据点的关系逐渐减弱。引入遗忘因子来减少早期观测数据对于拟合结果的影响。
定义观测数据队列长度为20,遗忘因子λi∈(0,1),与观测时间呈正比例关系,如式(3)所示。观测数据点越靠后,遗忘因子越大,相应观测数据点的准确度也就越高。

定义观测数据 (vi,ai)(i= 1,2,3,…,20) 为前20个采样周期观测到的速度和加速度值。列解关系式(4)求取各观测点到曲线偏差平方和L(w)最小时的关系式系数A,B和C。
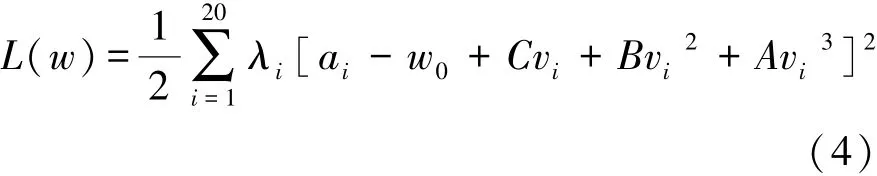
外界环境的变化会导致预测的基准加速度实时变化,可能会导致系统模式的频繁切换,将加速部件的磨损老化,也会导致车内乘员不舒适的驾乘感觉。因此,对切换基准加速度a0曲线上下定义2H的缓冲区间,定义缓冲区间H=0.1m/s2,如图3所示。当加速度达到区间上限a0+H时,系统进入驱动模式;当加速度达到区间下限a0-H时,系统进入制动模式;当加速度在区间内时,系统保持当前工作模式。
3 基于迭代学习的纵向控制策略
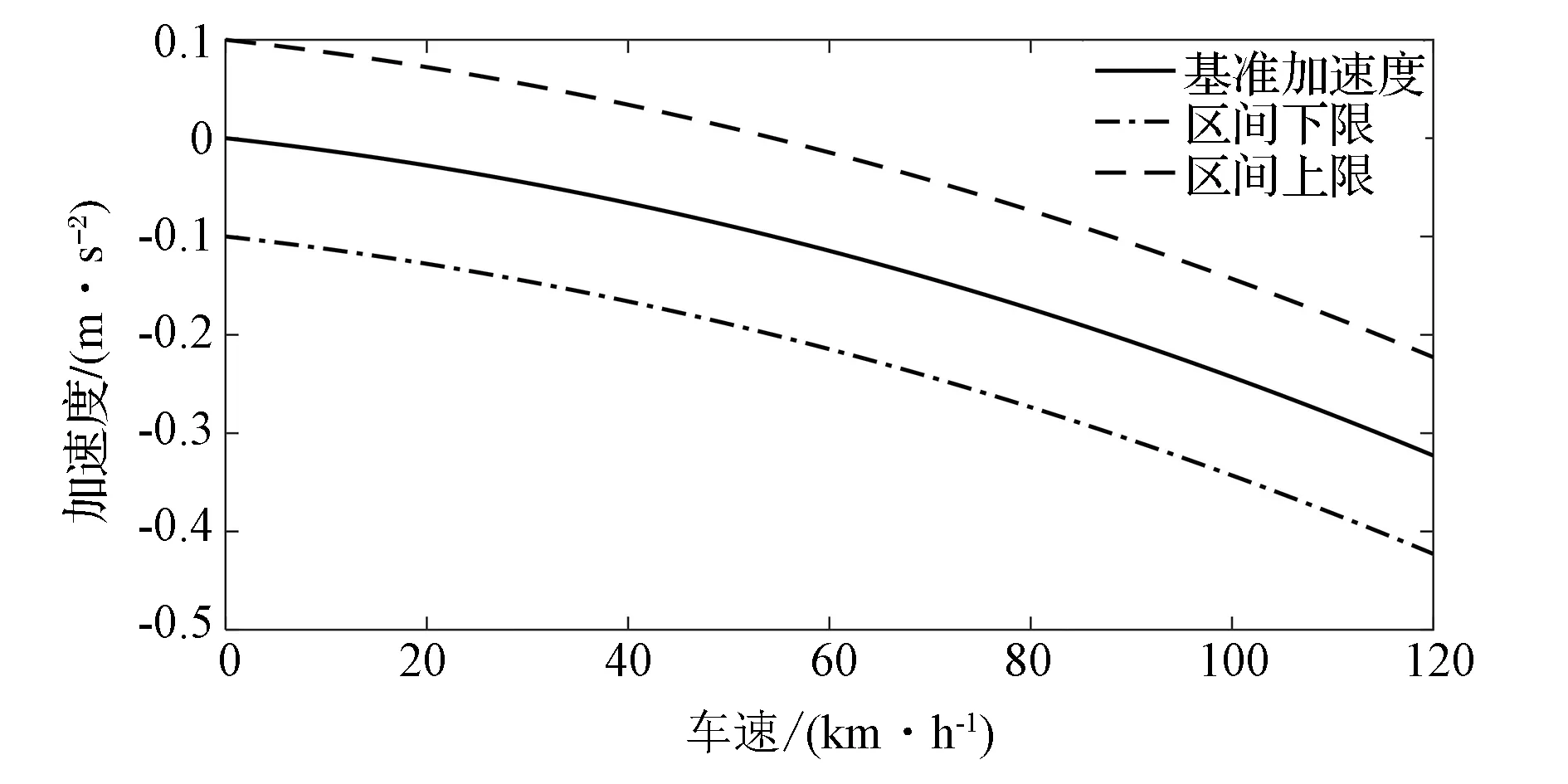
图3 模式切换曲线
自适应巡航系统纵向动力学控制策略的目标是控制执行机构使车辆加速度稳定跟随期望加速度的变化。第2节所述的模式切换策略计算得到的基准加速度可尽可能抵消道路坡度和风速对控制系统的干扰。目前研究人员主要采用的控制方法包括基于数值查表的控制方法、基于纵向动力学模型的控制方法和经典PID控制方法。
其中基于纵向动力学模型的控制方法,由于系统的强非线性和耦合性,很难构建出准确的数学模型,导致控制效果不精确。基于数值查表的控制方法,通过前期试验标定建表,准确度较高,然而针对于不同车型需要重新标定[9],因此该方法成本较高、移植性差。经典PID控制器方法结构简单,稳定性好,可靠性高。然而经典PID控制方法多基于时不变控制系统设计,当目标工作点快速变化时,控制性能较差[10]。
迭代学习控制方法是一种带有自学习能力的控制算法。其根据过去的输入和误差的跟随效果来优化当前控制输入。迭代学习控制方法不需要系统本身的精确模型,对于非线性系统和时变系统有着较强的适应能力[11]。
迭代学习控制系统结构为

式中:t∈[0,T],T表示一个工作周期;uk(t)为第k次迭代系统输入量;ek(t)为第k次迭代的输出误差量;yd(t)为期望输出量;yk(t)为第k次迭代系统输出量;U是学习律。迭代学习的基本原理是依据上一周期系统的控制量uk(t)和系统输出误差ek(t)对当前周期的控制量uk+1(t)进行修正。常用的迭代学习学习律主要有P型、PI型、PD型等。由于车辆纵向动力学控制具有一定的滞后性,利用PD型学习律构建驱动和制动的控制器:
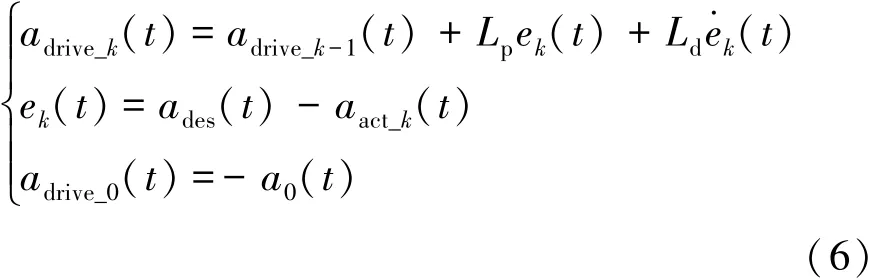

式中:adrive为输出至驱动系统的加速度修正量;abrake为输出至制动系统的加速度修正量;Lp和Ld为学习增益因子;ades为目标加速度值;aact为实际汽车加速度值;adrive_0和 abrake_0为迭代初值。
为了抵消外界行驶阻力变化对系统控制的干扰,设定迭代初值加速度为基准加速度作为补偿。
通过迭代学习算法可计算得到修正后加速度值,最后的控制量是电机驱动或制动转矩和制动系统轮缸压力。因此还需要对修正后的加速度作进一步的计算。
本文中纯电动汽车没有变速器,电机的转矩直接通过主减速器、差速器传递至车轮克服行驶阻力,电机驱动转矩为

式中:Tdrive为电机驱动转矩;M为整车质量;ades为期望加速度;Rtire为轮胎滚动半径;η为传动效率;i为传动比。
制动系统分为液压制动和电机制动,为更多回收能量,需要电机承担尽可能多的前轴制动力Ff_motor,不足部分由前轴液压制动Ff_hyd补偿。定义Cf和Cr分别为前、后轮液压制动力矩与轮缸压力转换系数,单位为N·m/MPa。则液压制动系统前轴轮缸制动压力pf、后轴轮缸制动压力pr和电机制动转矩Tbrake为

其中,前后轴制动力和电机制动力由制动力分配策略获得。
基于迭代学习的电动车ACC纵向控制方法流程如图4所示,由决策层算法产生期望加速度作为模式切换策略的输入。若模式切换策略仲裁为驱动模式,利用驱动迭代学习算法修正期望加速度,修正后的加速度转化为电机驱动转矩信号,发送至电机控制器。若仲裁为制动模式,利用制动迭代学习算法修正期望减速度,修正后的减速度输入至制动力分配策略,输出前后轴分配的制动力。前轴制动力首先由电机承担。电机由于受到外特性、电池SOC等因素影响,电机制动力可能无法满足前轴需求,此时由前轴液压制动力补偿。前、后轴分配制动力转化为电机制动转矩信号和前、后轴制动压力信号分别发送至电机控制器和制动控制器。
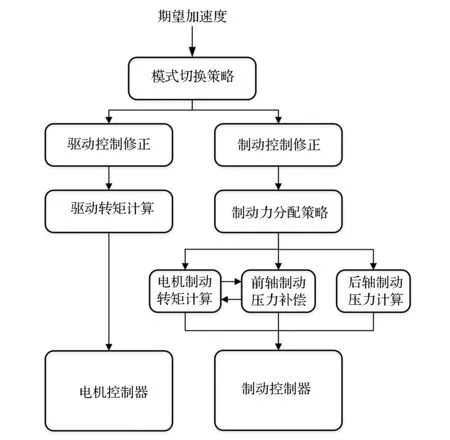
图4 纵向控制方法流程图
4 仿真与验证
为验证本文中构建的基于迭代学习的电动车纵向动力学控制方法在自适应巡航下的控制效果,首先需要构建自适应巡航的决策算法。根据文献[12]中的方法建立基于最优二次型的决策层算法。
定义控制指标函数:
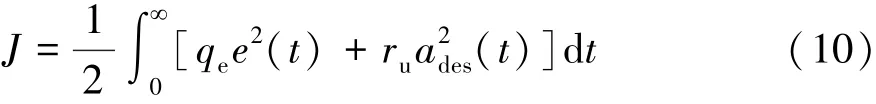
式中:e(t)为期望车间距与实际车间距的差值;ades(t)为输出的期望加速度;qe和ru为误差权值和加速度权值。考虑实际驾驶特性,取qe=10和ru=3,黎卡提方程求解整理得到:

式中:ades为期望加速度;y为车间距;dsafe为安全车间距;ah为自车加速度。定义外界风速50km/h,前车速度变化如图5所示。
车速、车间距跟随如图6和图7所示,基于最优线性二次型的ACC决策层算法对前车车速跟随和车距跟随效果较好。

图5 前车速度时间历程
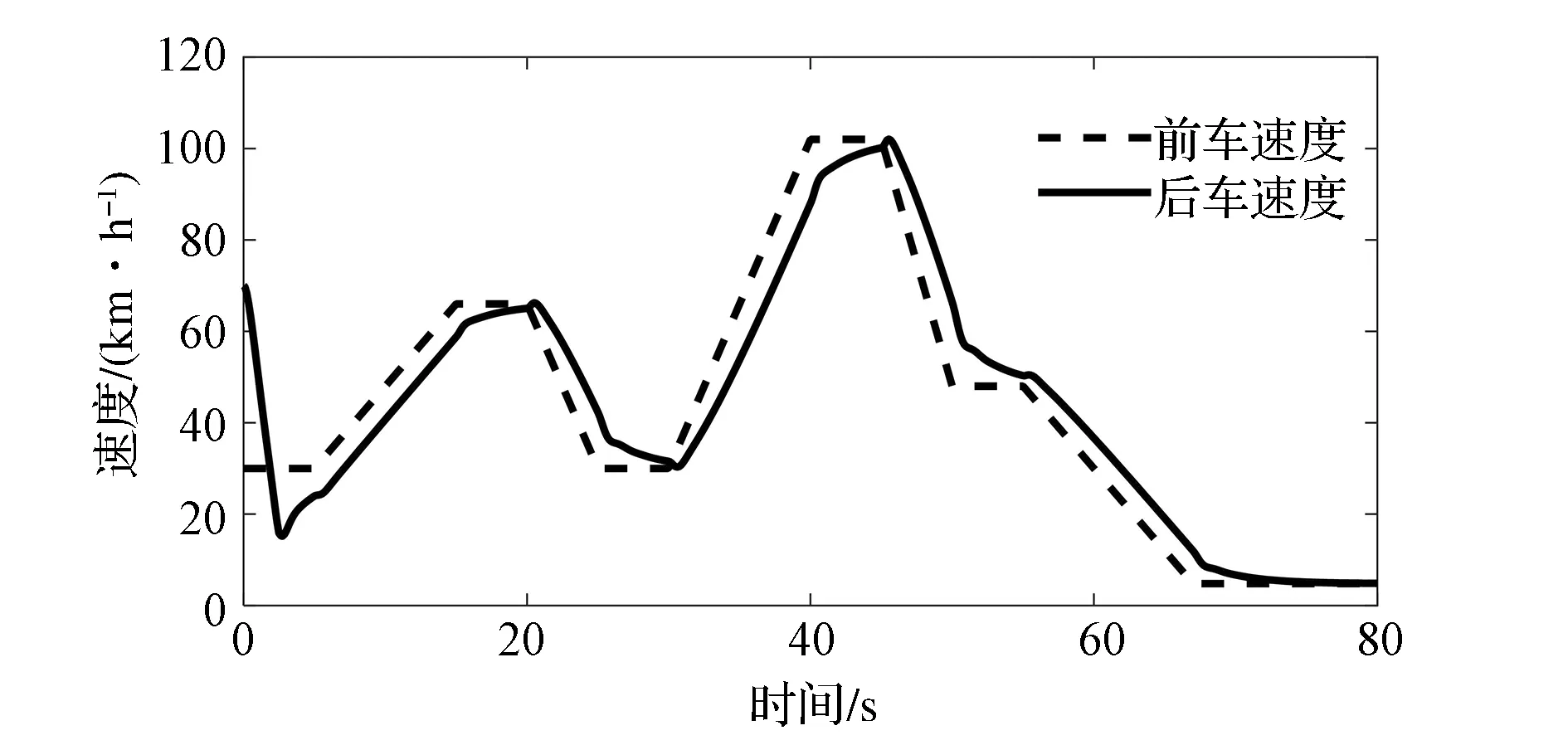
图6 车速跟随曲线

图7 车间距跟随曲线
前后轴制动压力分配如图8所示,电机转矩变化如图9所示。前期制动强度需求较高,因此前轴液压制动力、后轴液压制动力、电机制动力均参与制动。后期制动强度需求较少,主要为电机制动或电机和后轴液压共同参与制动。根据文献[13]中能量回收率计算方法,经计算仿真工况下的能量回收率为46.59%。
为验证本文中设计的基于迭代学习的纵向动力学控制方法有效性,选择传统的PID控制方法作为对比算法。模式切换策略基准加速度为0,若期望加速度大于0则进入驱动模式,若期望加速度小于0则进入制动模式,并采用式(10)建立的决策算法计算期望加速度。仿真结果如图10~图13所示。
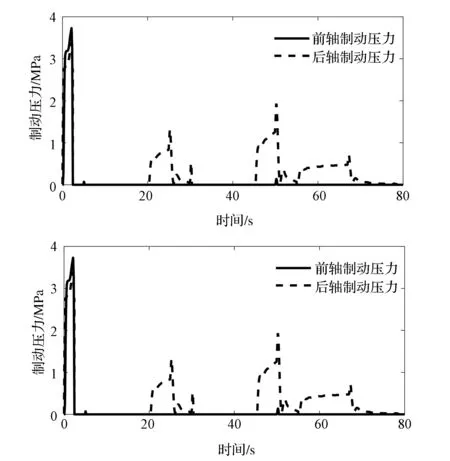
图8 前、后轴轮缸制动压力

图9 电机转矩时间历程

图10 车速跟随曲线
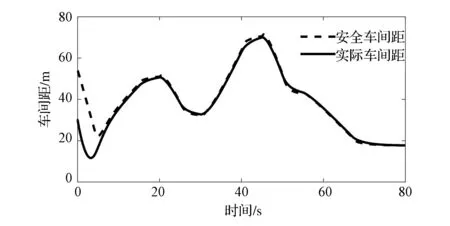
图11 车间距跟随曲线
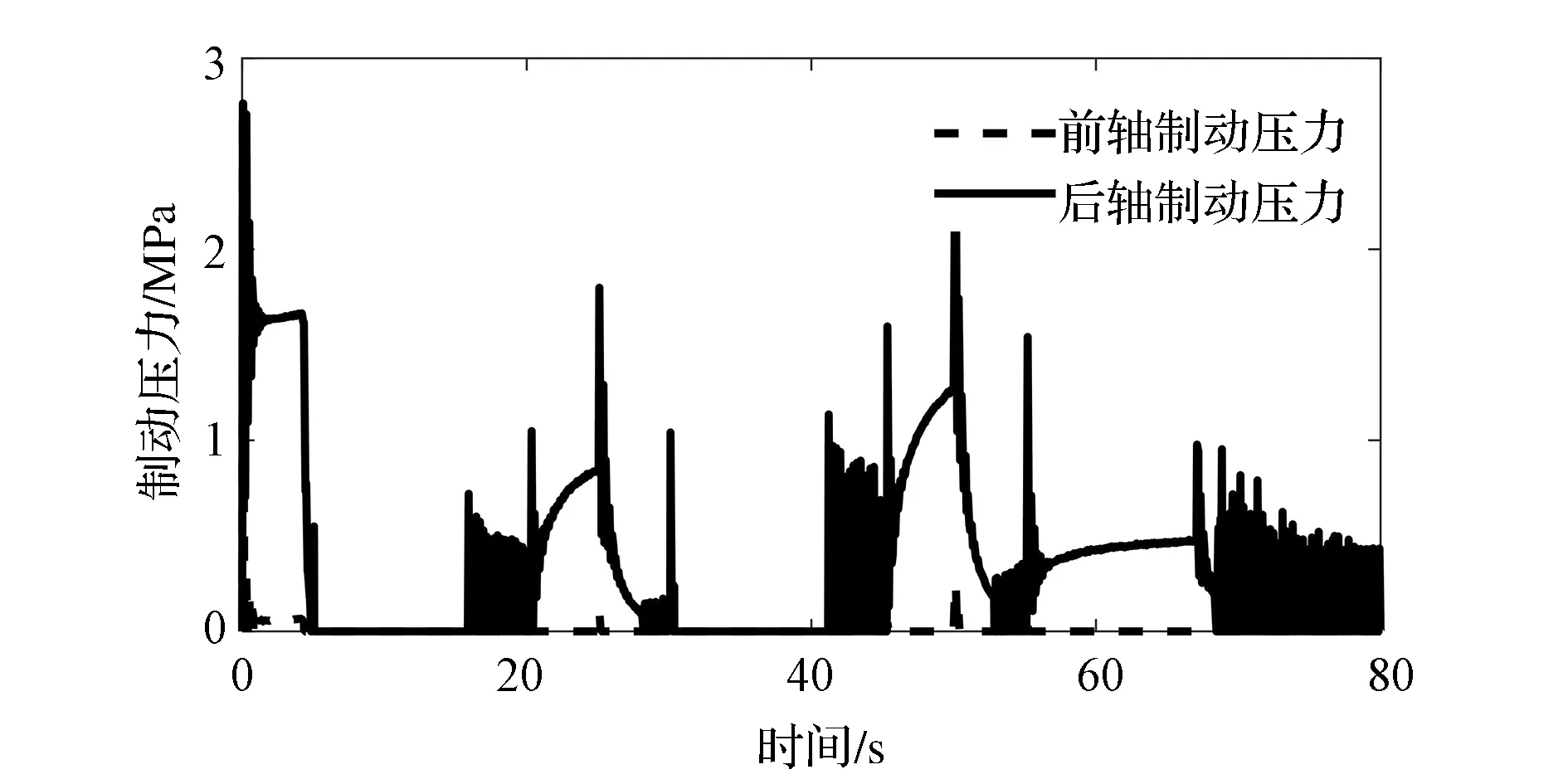
图12 前、后轴轮缸制动压力
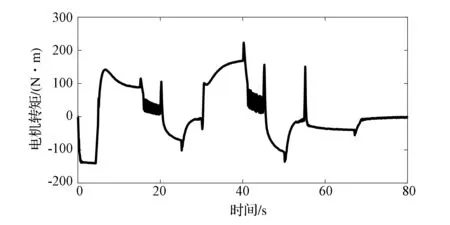
图13 电机转矩时间历程
由于决策算法相同,PID控制方法与迭代学习控制方法在车速跟随和车间距跟随效果上相近。而前后轴制动压力和电机转矩控制相比于迭代学习控制方法有较大的波动。为进一步比较两种控制方法的跟随效果,图14和图15列出了PID控制方法和迭代学习方法实际加速度对期望加速度的跟随曲线。PID方法期望加速度在基准加速度附近控制时,实际加速度出现较大的波动,驱动模式和制动模式频繁切换。在实车中若模式频繁切换会加快部件磨损,甚至失效。其原因主要在于风阻的干扰使基准加速度发生变化,而本文的纵向控制算法加入了对于基准加速度的实时拟合预测,并增加了切换阈值,使控制过程更为稳定。

图14 PID方法加速度跟随曲线
PID控制方法在期望加速度快速变化时,实际加速度对期望加速度跟随误差较大。其主要由于传统PID算法基于时不变系统设计。迭代学习控制方法由于在每一个控制周期均利用了上一周期的控制经验,并对这一周期的期望值做出修正,因此其对环境有一定的自适应性,实际加速度对期望加速度的跟随效果较好。

图15 迭代学习方法加速度跟随曲线
5 结论
提出一种前轴驱动纯电动轿车的自适应巡航纵向控制方法,具体包括设计了在自适应巡航系统下的制动能量回收制动力分配策略;基于加权最小二乘算法的驱动、制动模式切换策略;基于迭代学习的自适应巡航纵向控制方法,并在Matlab/Simulink和CarSim联合仿真平台下仿真验证,并与传统PID控制方法仿真结果进行对比,得出如下结论。
(1)基于最优线性二次型构建自适应巡航决策层算法,本文中纵向控制方法与传统PID控制方法均能实现自车对前车车速跟随和车间距跟随。
(2)PID控制方法在基准加速度附近工作时,出现模式频繁切换现象,本文中控制方法工作状态稳定。原因在于其模式切换策略可以实时拟合预测基准加速度,补偿风阻等外界环境变化对模式切换的影响。
(3)PID控制方法期望加速度跟随实际加速度有较大的误差,本文中控制方法实际加速度对期望加速度跟随性较好。其原因主要在于传统PID控制方法难以适应时变系统的控制。本文中基于迭代学习的纵向控制方法可根据历史输出数据做出修正,快速适应环境变化。
[1] 李朋,魏民祥,侯晓利.自适应巡航控制系统的建模与联合仿真[J].汽车工程,2012,34(7):622-626.
[2] LEE G D,KIM SW.A longitudinal control system for a platoon of vehicles using a fuzzy-sliding mode algorithm[J].Mechatronics,2002,12(1):97-118.
[3] 李以农,冀杰,郑玲,等.智能车辆自适应巡航控制系统建模与仿真[J].中国机械工程,2010(11):1374-1381.
[4] No ECE R.13:“Uniform Provisions concerning the approval of vehicles of categories M.N and O with regard to braking.”[S].United Nations Economic Commission for Europe,2003.
[5] YANG Y,CHU L,YAO L,et al.Study on the algorithm of active pressurization control of regenerative braking system in pure electric vehicle[C].SAE Paper 2015-01-2708.
[6] 蔡建伟.纯电动汽车全解耦式制动能量回收系统[D].长春:吉林大学,2016.
[7] IOANNOU P,XU Z.Throttle and brake control systems for automatic vehicle following[J].Journal of Intelligent Transportation Systems, 1994, 1(4):345-377.
[8] 余志生.汽车理论[M].北京:机械工业出版社,2009.
[9] 裴晓飞,刘昭度,马国成,等.基于节气门与制动联合控制的自适应巡航控制系统[J].汽车工程,2013,35(4):375-380.
[10] RAJAMANI R.Vehicle dynamics and control[M].Springer Verlag Gmbh,2006:27-31.
[11] JANSSENSP,PIPELEERSG,SWEVERSJ.A data-driven constrained norm-optimal iterative learning control framework for LTI systems[J].Control Systems Technology, IEEE Transactions on,2013,21(2):546-551.
[12] 马国成.车辆自适应巡航跟随控制技术研究[D].北京:北京理工大学,2014.
[13] 初亮,蔡健伟,富子丞,等.纯电动汽车制动能量回收评价与试验方法研究[J].华中科技大学学报(自然科学版),2014(1):18-22.
