某铝制乘用车白车身疲劳寿命计算

夏德伟，刘丽霞，徐志强，齐飞

（辽宁忠旺集团有限公司北京技术与发展中心，北京 100020）

引言

更换更轻质的白车身材料是新能源车发展的一种重要手段，铝合金因其轻质、可塑性强、回收性好等优良的性能被广泛使用。但与传统车相比，铝合金车身的应用技术并不是很成熟，所以在设计阶段借助于有限元分析技术以节约前期开发的成本且能有效提高整车的可靠性。一般针对白车身用到的有限元分析技术包括整车强度分析、刚度分析、碰撞分析、疲劳寿命计算等。

本文针对某铝制乘用车白车身利用前处理软件 Hyper-mesh和专业的疲劳分析软件 ncode对该车进行了疲劳寿命计算。从而，根据计算结果指出在该类型乘用车设计中，针对疲劳需要重点关注的位置。

1　模型的建立

本文研究的铝制乘用车有限元模型如图1所示：

图1　整车有限元模型

整车主要以S4R的单元类型进行网格划分，三角形网格占比小于 5%，其余网格质量控制参数也均满足有限元结果可靠性对网格的要求。

本文除建立了白车身的有限元模型外，还建立了悬架的简化模型。模型中利用SPRINGA单元模拟弹簧、CONN3D2单元模拟橡胶衬套、刚性连接模拟各点之间、轮心和对应点之间的连接。该简化建模方法既考虑了轮胎和白车身之间弹簧和橡胶衬套的联合作用，同时又避免了在疲劳分析过程中通过多体动力学对实测载荷谱进行转换这一繁琐过程。此类悬架简化方法的正确性已在其它项目研究中验证了它的正确性。

图2　右前悬架简化模型

2　疲劳分析过程

2.1　疲劳分析理论及流程简介

材料在循环载荷作用下，性能下降的过程称为疲劳损伤，当损伤累积到一定程度，就会发生疲劳破坏。一般疲劳寿命计算中通常用的累积损伤理论为Miner线性累积损伤理论[1]，损伤累积法则为：

其中：ni为某应力水平下的循环次数；Ni为该应力水平下发生破坏时的寿命；N为疲劳寿命。当D=1时，疲劳破坏发生。疲劳破坏分为高周疲劳和低周疲劳，分界标准为循环次数是否大于103。

图3　典型的S-N曲线和E-N曲线对比图

高周疲劳一般基于材料的S-N曲线进行疲劳分析，低周疲劳为E-N曲线。本文在分析中采用前者。

一个典型的疲劳分析流程图为[2]：

图4　疲劳分析流程图

以该分析流程为指导，以下逐一说明每一部分涉及到的参数设置、计算过程等。

2.2　应力场

在Hypermesh中，设置白车身的25个工况，包括白车身正常工作状态和车轮中心单位力和单位力矩作用的工况，具体设置为：

表1　工况设置

其中，工况1的载荷施加在各部件安装所对应的位置，工况1的边界条件和工况2-25的载荷施加在简化悬架对应的轮心位置处。设置工况1的目的是观察车身在静载工况下，应力值较大的位置，从而在一定程度上可以预测疲劳失效的位置。工况1的局部应力云图：

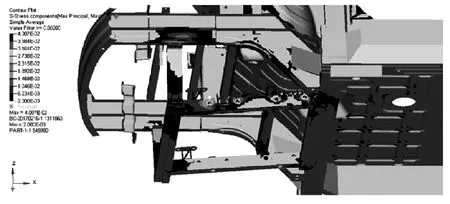
图5　工况1前副车架部分计算应力云图

从整车应力云图可以看出，白车身应力较大的位置集中在前、后副车架和钣金件弧度较大位置。这也通常是最容易发生疲劳的位置。

将2至25工况计算得到的odb文件作为白车身疲劳分析应力场的输入，以工况2为例，计算应力场为：

图6　工况2前副车架部分计算应力云图

得到的整车24个单位力作用下的应力云图分布后，可以作为整车疲劳分析的应力场。

2.3　材料的S-N曲线

一般，材料的S-N曲线定义了在应力比R=-1时，应力和循环次数的关系。幂函数是描述材料S-N曲线最常用的经验公式[3]：

其中，m、C是与材料、应力比、加载方式等有关的参数，对以上公式两边进行对数变换，可知应力S和寿命N之间为线性对数关系。

获取S-N曲线的方法有实验测量、经验公式推导和利用软件自动生成。本文利用 Ncode软件，以白车身中用到的材料 AL-6061为例，根据材料的强度极限自动生成如下曲线：

图7　AL-6061的S-N曲线

由于铝合金材料不表现处无限寿命特征，所以其寿命曲线的第二阶段为非水平线，这样得到的结果更接近实际。

2.4　载荷谱

在整车分析中，载荷谱由路试中六分力轮测得的数据进行处理后得到。为了节省计算时间，本文从综合路的载荷谱中截取10S的短波路载荷谱数据为例进行疲劳分析。如图：

图8　短波路况下左前轮载荷谱

图9　左前轮1方向载荷谱频率分析

图10　左前轮1方向载荷谱雨流分析

以左前轮1方向载荷谱数据为例，在Ncode中对载荷谱数据进行频谱和雨流分析，可以看到载荷谱的频率在 50HZ以下，雨流矩阵表明数据从小量程到大量程循环次数逐渐递减，近似成高斯正态分布。从数据分析可以看出现有载荷谱满足疲劳分析的要求。同时，由于载荷谱的应力比不等于-1，所以在疲劳分析时采用较为保守的 Goodman方法来修正平均应力对结果的影响。

在对整车进行疲劳分析时，一般会通过多体动力学软件将轮心处的载荷谱转换到白车身与悬架的连接点或者整车比较关注的位置处。但从文献[4]知，悬架连接点的载荷和轮心处的载荷相比，幅值基本一致，只是有微小的时间延迟，这并不会对车身的疲劳产生显著影响。所以，本文中，建立了图2所示的简化悬架模型，模型中考虑了弹簧和橡胶衬套的作用，在2至25工况中，直接将单位载荷加载在对应的轮心处。这种方法明显简化了通用的整车疲劳分析步骤。

2.5　疲劳分析流程

在Ncode建立疲劳分析流程图：

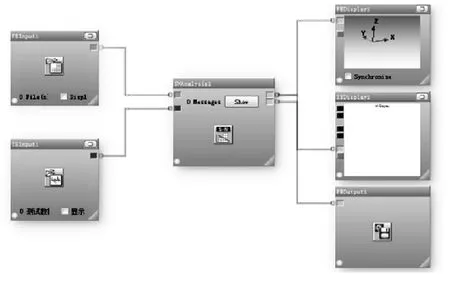
图11　经典疲劳分析流程图

将以上各数据输入该流程图中，对整车疲劳分析。

2.6　结果

通过计算，得到整车的寿命分布，可知，整车寿命较小的位置集中在整车前后副车架，如图：

图12　前后副车架寿命云图分布

经疲劳分析知整车寿命最低的位置为后副车架中吊耳与型材连接处，节点编号为1281139，循环次数为2.454E6，对应的寿命为6.8E3h。寿命较小的各点的信息如表：

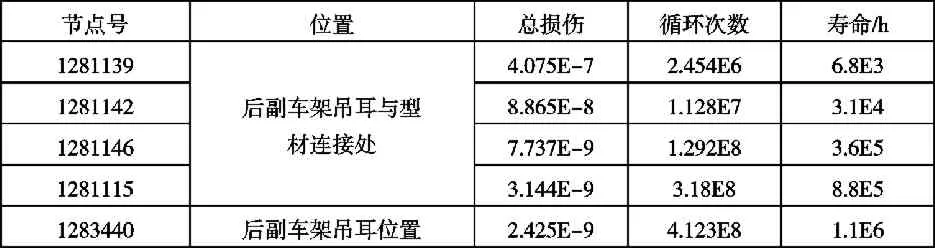
表2　整车疲劳值较小的位置及寿命

3　结束语

本文在对白车身进行疲劳分析时，除了建立的整车的有限元模型外，还建立了简化的悬架模型，且模型中考虑了在静力分析时悬架中弹簧和橡胶成套的作用，简化了整车疲劳分析的步骤；

经过对整车的疲劳分析可以看出，白车身在短波路路况下，容易出现疲劳的位置为前后副车架、和车身上部与悬架连接的地方，尤其是结构刚度过度不均匀处，这也正是工况1-25所示的应力值较大的位置。且从分析结果中看出前几个影响整车寿命的位置集中在某几个点，如果对这前几个位置进行优化，会显著提高整车在疲劳计算时的寿命。

[1] Miner M A, Calie S M. Cumulative damage in fatigue[J], J Applied Mechanics, 1945, 12: 159-164.

[2] 刘永臣,王国林,孙丽.基于实测载荷谱的副车架疲劳寿命估算方法[J].汽车技术, 2014(04): 58-62.

[3] 姚卫星. 结构疲劳寿命分析[M].北京:国防工业出版社, 2003

[4] 沈磊,张守元,郁强,张一京.轮心六分力作用下车身疲劳寿命分析与改进[J]. 轻型汽车技术, 2012(Z2): 17-21.