双阶自适应小波聚类的航空发动机故障分类与识别
2018-04-10左红艳刘晓波洪连环
左红艳 刘晓波 洪连环
摘要:为了快速准确地实现航空发动机转子故障的分类与识别,提出了双阶自适应小波聚类方法。双阶自适应小波聚类过程是:首先采用粗网格量化数据空间,找出存在聚类的空间区域,实现数据的预分选聚类;然后统计子聚类的信息,计算其二次聚类的量化值;最后对子聚类的数据空间进行自适应细划分,实现子聚类数据空间的小波聚类。应用双阶自适应小波聚类方法对航空发动机转子的正常、不对中、碰摩、松动故障进行分类与识别,结果显示4种类型被正确分类。因此表明,对于密度分布不均匀的多类型混合数据,双阶自适应小波聚类方法能够根据数据分布特点自适应的量化网格,实现故障的正确分类与识别,诊断精度显著高于传统的小波聚类方法。关键词:故障诊断;航空发动机;小波聚类;双阶自适应;聚类精度
中图分类号:TH165+.3;V23 文献标志码:A 文章编号:1004-4523(2018)01-0165-11
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.020
引言
航空发动机转子故障诊断的关键环节是模式识别,就是应用数学方法对蕴含相关故障信息的数据模式进行自动处理和判别,从而提取出有效诊断规则,对故障数据进行的智能分类。
当前应用于航空发动机转子故障的模式识别与分类方法主要有人工神经网络、支持向量机、遗传算法、贝叶斯分类和决策树等,但这些方法都是有监督的学习方式,要通过训练样本的训练学习才能有效地处理未来要分类的数据,并且数据在分类之前还需要指定要分类的类型和分类数,使得分类时间长、效率低,并且诊断的准确率受训练样本精确度的影响较大。
无监督学习的聚类分析是机器学习领域中的另一个重要分支,它通过某种相似性度量,对输入样本进行分类。无监督的聚类算法有基于划分、层次、密度和网格方法。其中基于划分、层次和密度的聚类方法是通过数据点之间的相似性判断数据点集是否属于同一聚类,因此其时间复杂度较大,聚类过程效率低;而基于网格的聚类方法把对象空间量化为有限数目的网格单元,形成一个网格结构,所有的聚类操作都在这个网格结构上进行,这种方法的主要优点是它的处理速度很快,其处理时间独立于数据对象的数目,只与量化空间中的网格单元数目有关,并且能够得到任意形状的聚类。小波聚类算法是基于网格聚类的典型算法,它是将信号处理技术中的小波变换和数据挖掘中的网格聚类算法有机结合形成的一种基于网格和密度的联合算法,因此小波聚类方法具有网格聚类的优点,如无监督指导聚类、运行速度快、能有效处理大数据集、能发现任意形状的簇等。由于小波变换技术的融入,小波聚类方法能够对数据进行有效去噪,使聚类结果不受噪声影响,并且能够在不同的尺度空间上发现聚类。基于小波聚类的优点,小波聚类分析方法被应用于图像处理,模式识别及故障诊断领域。故本文选择应用小波聚类的方法实现航空发动机转子系统的故障诊断。
小波聚类分析方法的聚类精度非常依赖于网格量化值及密度阈值两个参数的选择,给出最优量化值及阈值,是得到高精度聚类结果的关键。如果量化值太高,同一簇类会被分成为几个小类,或作为孤立点丢失;量化值太低,本应分开的簇可能被合并成同一个簇类;并且小波聚类的边界精度受阈值影响较大,如果边界单元数据小于密度阈值时,网格单元被作为低密度单元舍弃,聚类边界精度受损,如果网格密度阈值太小,则包含有噪声的低密度网格单元被当作高密度单元聚类,使聚类结果不准确。特别是不均匀分布的数据类型,很难取到一个合理的量化值和相似度阈值,实现正确的故障识别与分类。
为了能够快速准确并且无监督地实现航空发动机转子的故障诊断,本文提出了双阶自适应小波聚类分析方法,此方法在保持了小波聚类分析方法的诊断速度快、效率高的基础上,可自适应选取二次细划分的量化值,消除网格量化值及密度阈值的参数设置对诊断准确度的影响,提高故障诊断精度。
1双阶自适应小波聚类算法的描述
双阶自适应小波聚类就是对预分类的数据集应用两次聚类:首先应用大网格划分,实现数据的预分选聚类;其次根据预先分聚类信息,对每个子聚类二次网格细划分,实现小波聚类,因此称为双阶自适应小波聚类分析方法。双阶自适应小波聚类的过程:第1步,采用粗网格划分,找出存在聚类的子空间区域,实现故障预分选聚类。由粗网格划分得到的各个聚类,称为子聚类;第2步,统计子聚类信息,计算网格单元二次划分的量化值;第3步,提取各子聚类区域数据及信息,自适应细划分网格,实现二次小波聚类;第4步,输出自适应细划分网格的聚类结果。其中自适应细划分量化值的计算是双阶自适应小波聚类实现的关键点。双阶自适应小波聚类算法总流程如图1所示。根据双阶自适应小波聚类过程的4个阶段,下文详细叙述每一阶段的算法及步骤。
1.1粗划分预分选聚类
粗划分预分选聚类是双阶自适应小波聚类的第一阶段,其流程图如图2所示。
粗划分预分选聚类的过程如下:
步骤1:输入信号特征向量点集X;粗划分量化值k;密度阈值w;广度优先相似度值。
密度阈值w:根据数据分布特点,给出一个经验值。
广度优先相似度值:指相邻网格之间的欧几里德距离,例如相邻网格单元Ui和Uj间的欧几里德距离如下式所示
步骤2:量化网格单元,用胞元数组C存储每个网格单元。
计算数据点集X每一维上的最大值hi、最小值li及步長si。将d维数据空间的每一维均匀等划分为步长为si的k等份。从而将整个数据空间划分成kd个不相交且大小相等的矩形单元。将数据X投放到网格单元C中,各个网格单元Ci存储其区间范围内的数据点集。
步长si计算式为
步骤3:统计每个网格单元中的数据点数den(ci),当den(ci)大于密度阈值w时,此网格单元为显著网格单元,提取胞元数组C内的显著网格单元数据及显著网格单元的位置标签存储于新建信息表C1的第1列及第2列。C1存储表结构如图3所示。
步骤4:根据C1第2列的位置标签形成距离矩阵,应用广度优先搜索连通相邻显著网格单元实现聚类。显著网格单元的聚类标识存储于信息表C1的第3列。属于同一聚类的,用同一个数字标识,例如所有标识为“1”的显著网格单元属于同一个聚类,称为第1聚类;聚类标识为“h”所有显著网格单元属于同一个聚类,称为第n聚类。
图3的第4,5,6和7列的信息,是由后序的统计与计算过程得到,并存储到图3的4,5,6和7列内的,在此简要说明,子聚类信息计与存储章节有详细叙述。
由于粗聚类网格较大,导致粗聚类的精度低。因此,用自适应细化网格方法对子聚类网格单元进一步细划分并且小波聚类,提高边界精度和分类正确度。
1.2子聚类信息统计与存储
为了对粗网格预分选得到的子聚类数据空间二次自适应细划分,需要对子聚类信息进行统计与计算,为自适应细划分小波聚类提供信息支持。其中自适应细划分量化值的计算是双阶自适应小波聚类实现的关键点,细划分量化值选取理论公式是以子聚类中的最大网格密度与最小网格密度之比为判断依据,对细划分量化值计算公式进行了理论推导,并给出了细划分量化值的计算公式。
1)细划分量化值ki的计算
经过了预分选聚类,同一个子聚类的数据分布基本一致。进一步细划分网格聚类的目的是计算一个优化的量化值ki,使细划分后的网格单元密度达到基本一致,也就是内部最大网格单元密度与边界网格单元密度一致,提高边界精度。如果数据分布越均匀,细分后的网格单元密度越一致,最大网格密度dmax与最小网格密度dmin之比b逼近为1。
粗网格单元被细划分一次,每一维等分为2份,网格容积为原网格的2-d(d是数据维数)。如果划分z次,每一维等分为2z份,细分网格的面积变为原来的2一如,当z取到一个合理值,细分后的网格单元密度与边界单元密度达到基本一致,最大网格密度与最小网格密度的密度比6可逼近1。如图4所示,二维数据网格每一维划分1次,面积变为原来1/4,划分2次,面积变为原网格的1/16,划分3次,细划分网格为原粗网格面积的1/64。假定边界网格密度为最小值dmin,细化分后的边界点被划分到了同一个细化网格中,那么细网格单元的边界密度是dmin/2-dz与粗网格中的最大密度dmax基本一致。由此得到关系式为
(3)由式(3)可得出密度比6的关系式为
(4)
2)子聚类信息统计与存储
每个子聚类的信息统计结果存储于图3所示C1中。显著网格单元密度d,存储于C1第4列中;子聚类网格最大密度与最小密度比称为密度比6,存储于C1各个子聚类的第1行的第5列;利用公式(6)计算各个子聚类的网格单元的划分数z,存储于C1各子聚类的第1行的第6列;统计各个子聚类的每一维网格单元数mi,根据式(7)计算出各维的量化值,计算各个子聚类中的数据在每一维上的最大值与最小值,子聚类数据的第i维向的最大值定义为最大边界值,最小值定义为最小边界值,形成d×3矩阵,如下式所示存储于C1子聚类的第1行的第7列。
计算式(8)中的边界信息与量化值的目的是为每个子聚类的二次聚类提供网格单元的量化参数,也就是根据每一维上的量化值ki、网格边界himax和jimin,在每一维的最大值jimax与最小值jimin之间的范围内再次划分成为等份。
3)建立信息映射表Cz
从粗聚类的信息列表c1中,分类提取同一个子聚类的统计信息,分类存储于新建Cz{n,1}信息表中,如Cz{i,1}存储第i个子聚类的统计信息。提取Cz{n,1}的信息,用于后续的自适应小波聚类,自适应小波聚类后的信息存储到Cz{n,2}。信息存储表Cz的建立,使得粗网格预分选子聚类与自适应小波聚类建立了映射关系,及最终的聚类结果与原始数据之间建立了映射关系。
1.3子聚类的二次细划分及小波聚类
子聚类的小波聚类过程如图5所示。
自适应细划分小波聚类的步骤如下:
步骤1:提取Cz{n,1}单元内的第1列的数据信息Xi,及Cz{n,1)单元内第7列的数据信息:最大边界坐标jimax、最小边界坐标jimin、量化值ki,作为自适应小波聚类的输入信息。
步骤2:根据每一維上的量化值ki,网格边界jimax,jimin,根据式(2)计算步长si。
步骤3:量化子聚类网格单元,将子聚类空间量化成k1×k2×…×ki个不相交且大小相等的网格单元C。
步骤4:数据Xi投放到单元C中,各个网格单元C'i存储其空间范围内的数据点集。
步骤5:统计每个网格单元中的数据点数den(C'i),当den(C'i)大于密度阈值W时,此网格单元为显著网格单元,提取显著网格单元内数据及显著网格单元的位置标签存储于新建信息表C3的第1列及第2列。C3存储表结构如图6所示。
步骤6:对显著网格单元内数据实施小波变换,提取小波變换系数,存储于信息表C3的第3列。
步骤7:根据C3第2列的位置标签形成距离矩阵,应用广度优先搜索原则,在小波变换后的特征空间中连通相邻显著网格单元实现聚类。聚类标识存储于信息表C3的第4列。
步骤8:将C3信息存储表存放到相应的Cz{n,2}中,并输出聚类结果图,用色彩区分不同的聚类。
步骤9:循环步骤1至8,直到n个子聚类自适应细划分小波聚类完成。
步骤10:输出信息存储表Cz,比对样本数据,判断聚类标识分别属于哪类故障,并标识故障类型。
2航空发动机转子故障诊断的模拟实验与分析
2.1数据采集及样本分析
本文验证所用数据在南京航空航天大学智能诊断与专家系统研究室的航空发动机转子试验器上采集,航空发动机转子试验器的真实图片如图7所示,剖面图如8所示。利用试验器模拟发动机转子正常、不对中、及涡轮叶片与机匣封严间隙处的碰摩、轴承松动4种故障状态。不对中故障设置是调整安装台架上的支承件,使发动机位置发生变化,导致发动机的输入轴“6”与电机的输出轴不对中,从而造成联轴器不对中故障;碰摩故障设置是首先将发动机旋转到一定转速,然后,用板手拧碰摩环点变形顶螺栓“5”,使碰摩环“1”产生变形,从而与旋转的涡轮叶片产生碰摩。轴承松动的设置是使与滚动轴承外圈配合的轴承支承孔增大,使配合为间隙配合,从而造成轴承松动故障。
振动信号的测试位置选择如图8所示,对测试点的采集样本进行了分析,选择后承力机匣垂直方向的测试点4y的振动加速度信号为故障诊断的分析样本。
测试点4的采样频率为10240Hz,样本长度8192,其中正常样本153组,不对中样本126组,碰摩样本101组,松动样本154组.从采集的各种故障状态下的样本中各提取了一个进行样本分析,分别为原始信号时域波形图、Hilbert边际谱、小波分解的最大能量层的功率谱。如图9~12所示,航空发动机转子系统运转时,在不同的故障状态下,振动信号的特征频率不同,可作为识别航空发动机故障的重要特征,故提取了边际谱的功率谱重心、小波分解层最大能量层的功率谱重心两个特征向量用于故障的分类及识别。
边际谱重心提取是首先对振动加速度信号采用自相关方法降噪,再用Hilbert-huang变换得到Hilbert谱,最后将信号所有时刻某一瞬时频率的能量加起来,从而得到Hilbert边际谱;最后计算其边际谱重心h1。
最大能量层的谱重心提取是通过小波分解,提取小波分解的最大能量层,然后计算最大能量层的功率谱重心h2。谱重心h1和h2由下式计算得到
(9)式中ωi为频率值,ωz为转速频率值,h(ωi)为ωi频率的能量谱,N为频率分段数。由式(9)可看出,频谱重心以基频为基准,作了归一化处理。因此计算得到的功率谱重心是一个无量纲参数,目的是消除不同的转速对功率谱重心值的影响。
利用h1和h2生成一个点数为534的二维特征向量组X,其数据分布如图13所示。可看出,数据大体分为4类,其中包含少量远离簇类的孤立点。在信号样本采集时,由于航空发动机运转过程中的随机振动或运转不稳定引起的特征值变化较大导致的,文中将这些远离聚类的孤立点定义为噪声。正常与不对中的数据分布集中,但两类数据的分布位置较近,右上角的松动故障的数据分布松散。由于不同的故障类型,采集到的信号的稳定程度不同,导致其特征向量的分布密度不同。
2.2单阶小波聚类的故障诊断
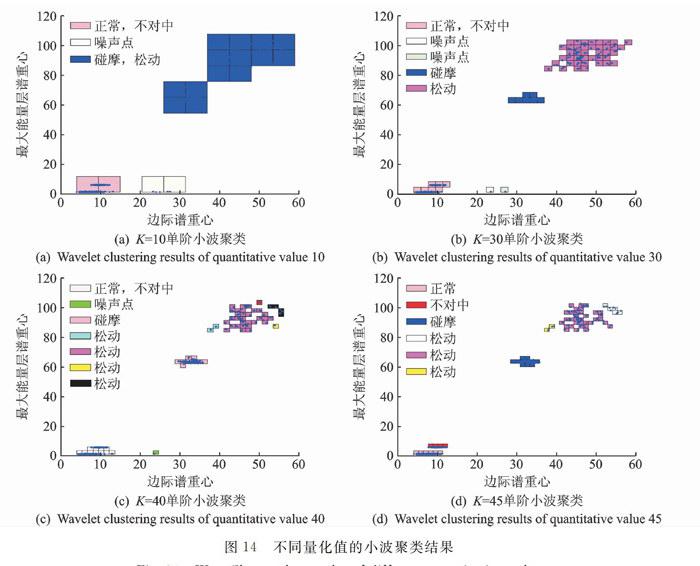
本文首先对二维特征向量X,应用单阶小波聚类方法对4种转子故障进行模识识别与分类,图14为不同量化值k的小波聚类结果比较,不同的颜色表示不同的聚类。当量化值k=10时,由于网格划分太大,距离较近的正常、不对中故障被聚为一类、碰摩与松动故障被聚为一类;当量化值k=30时,碰摩与松动故障被正确聚类,但正常、不对中故障还是被聚为一类;当量化值k=40时,正常、不对中故障不但没有区分开,并且随着量化网格的变小,在分布图上,数据分布松散的松动故障数据中间被划分出了多个空网格,使得同一个松动故障类被聚成了多类;当量化值k=45时,正常、不对中故障终于聚为两类,但松动故障由于量化网格变小,还是被聚成了多类。也就说,密度集中的数据需要的最优量值比较大,即量化为较小的网格;密度分布松散的数据需要的最优量化值比较小,即量化为较大的网格。当分布密度不一致的航空发动机的故障数据混合在一起,用统一的量化值去量化网格时,是不能取到一个适合于所有数据的最优量化值,所以用单阶小波聚类方法,用一个统一的量化值k,不能实现故障数据正确分类与识别。所以应该根据数据密度分布特点,选取不同的量化值,才能得到正确率高的故障分类结果。
2.3双阶自适应小波聚类的故障分类过程
(1)粗网格划分聚类
输入二维特征向量数据集X,及粗网格划分量化值k,及密度阈值w,此诊断实例给出的粗网格划分量化值k=20,密度阈值为2,粗网格划分的量化值的大于估算分类数就可,但初始量化值不要太大,如果太大,会导致分由松散的数据被分成多类。对数据实现初次预分选聚类;粗聚类的结果信息存储到图15所示的信息表中的1,2,3,4列。图15为粗网格聚类的存储信息,第1列内容为显著网格单元内的数据;第2列内容为显著网格单元的位置标签;第3列内容为小波变换后显著网格单元内数据;第4列内容为聚类标识,相同的标识为同一聚类;
(2)统计及计算粗网格预分选的聚类得到的每个子聚类信息
统计及计算统计预分选的每个子聚类信息,存储到图15的5,6,7列,为每个子聚类的二次聚类提供子聚类的二维数据点Xi、子聚类的数据边界、及每个子聚类再次聚类的量化值。图15信息存储表的第5列内容为统计的显著网格单元的密度,也就是数据个数;第6列内容为同一个子聚类内,每个网格再次被细划分的格数,是由式(6)计算得到,同一子聚类,每个网格再次被划分的格数是相同的,因此,只需要存在同一个子聚类的第一行就可以;第7列存储子聚类的z向的数据分布的最大边界jxmax、最小边界jxmin、量化值kx;y向的数据分布的最大边界jymax、最小边界jymin、量化值ky,子聚类z,y方向的边界信息是统计子聚类所有数据信息得到,量化值kx,ky根据数据并根据公式(6)计算得到,因为每个子聚类x,y方向的格数不同,所以每个方向的量化值是不同的,但是每个粗网格再次被分成的格数是相同的,7列的信息只需要存储在每个子聚类的第1行即可。
(3)提取每个子聚类的信息,进行二次细划分聚类,并且建立信息映射表Cz,如图16所示。
1)从粗聚类的信息列表C1中,分类提取每个子聚类的统计信息,分类存储于新建Cz{n,1}信息表中,如Cz{i,1}存储第i个子聚类的统计信息。如图16所示
2)提取Cz{n,1}单元内的第1列的数据信息Xi,及Cz{n,1)单元内第6和7列的数据信息。
3)根据6列的信息判断此子聚类是否需要二次聚类,算法设定网格还需划分值如果大于2,需二次聚类,小于等于2,不需要二次聚类。
4)如果需要二次聚类,将数据信息Xi、最大边界坐标jimax、最小边界坐标jimin、量化值ki,作為二次小波聚类的输入信息,实现对数据信息X实现二次聚类。二次聚类后的信息存储到Cz{n,2},再次分类提取Cz{n,2}内信息,存储到Cz{n,3}中。信息存储表Cz的建立,使得粗网格预分选子聚类与二次小波聚类建立了映射关系,及最终的聚类结果与原始数据之间建立了映射关系。
图17为二维特征向量X的双阶自适应小波聚类结果。聚类结果为4类,4种类型的故障被正确分类与识别,诊断正确率为96.82%。在应用双阶自适应小波聚类时,只需给出一个粗量化值k,并且这个值不需优化,只要量化值k大于样本的估算分类数即可。双阶自适应小波聚类算法会根据预分选子聚类的数据信息,对每个子聚类自适应划分,得出正确的聚类结果。
2.4其他故障诊断方法与比较
常用于转子故障诊断方法有模糊c-均值(Fuzzy C-means algorithm,简称FCM)聚类方法、自组织特征映射神经网络(self organizing featuremap neural network,简称SOM)和支持向量机(Support Vector Machine,简称SVM)。本文用FCM,SOM及SVM对特征向量数据X进行故障分类与识别,所用特征向量数据X与单小波聚类、双阶自适应小波聚类实例中的数据是同组数据,图18为FCM诊断结果,图19为SOM聚类结果,由此可见,FCM和SOM聚类方法都没有将距离较近的正常、不对中分开,并且松动故障被误分成两类。图20为SVM分类结果,分类结果正确率比较高,此支持向量机是在4类故障样本中各提取40个,共160个训练样本和径向基核函数训练生成的。方法在诊断精度及诊断效率两个方面与量化值为45的单阶小波聚类、FCM、SOM及SVM的比较。从表1可以看出,针对于密度不均匀的数据,自组织特征映射神经网络(SOM)的诊断方法所耗时间最长,诊断的准确率较低,并且FCM与SOM都需要预先指定分类数。SVM方法的诊断精度较高,并且数据分布密度对诊断结果影响很小,但SVM的诊断精度与训练样本的准确度、核函数的选取等参数有关,如果提高训练样本的精度及样本数量,并且能通过大量实验来确定最优参数,SVM的正确率还会高于表1所示的诊断正确率,但SVM的诊断时间,大于双阶自适应小波聚类。对于大数据的分类与识别,双阶自适应小波聚类的诊断效率高,并且不需要重多参数的优化与选择,也无需指定分类数,可以实现无监督指导聚类。
3结论
(1)双阶自适应小波聚类方法是,首先采用粗网格量化数据空间,找出存在聚类的空间区域,实现数据的预分选聚类;然后统计子聚类的信息,计算其量化值;最后对子聚类的数据空间进行自适应细划分,实现子聚类数据空间的小波聚类。此算法的关键点是每个子聚类量化值的计算,本文以预分选聚类所得的每个子聚类的最大网格密度与最小网格密度之比作为计算与判断的依据,以子聚类被二次量化后的网格最大密度与最小密度之比逼近1为目标,推导出了每个子聚类二次量化所需要最优量化值的计算公式。
(2)本文应用双阶自适应小波聚类算法,对于航空发动机转子的正常、不对中、碰摩、松动故障的进行了分类与识别。此方法能够根据航空发动机转子故障特征值分布不均匀的特点,首先对数据空间进行粗划分预分选聚类,然后对预分选聚类所得的每个子聚类进行信息统计,计算每个子聚类的二次网格划分的最优量化值,实现子聚类空间的二次小波聚类。此方法消除了传统小波聚类方法使用统一个网格量化值对诊断精度的影响,并且避免了最优量化值的搜索过程,提高了故障诊断正确率。