乘客—车辆—桥梁耦合振动分析
2018-04-10王少钦彭培火杨谆马骎张田
王少钦 彭培火 杨谆 马骎 张田
摘要:为了更加准确地对乘车舒适性进行评价,建立了乘客一车辆一桥梁系统耦合振动分析模型,通过拉格朗日方程推导了系统的动力微分方程,Newmark积分进行迭代计算,采用Fortran语言编程进行求解,分别计算了桥梁、车辆及乘客的振动响应,并与通常的车辆一桥梁耦合振动模型计算结果进行对比。结果表明:是否考虑乘客模型对于桥梁的位移影响比较有限,但是对于车辆的振动状态会产生明显影响,且车辆与乘客的运动响应存在明显差异,因此采用车辆的振动响应对乘车舒适性进行评价的方法可能会过高地估计乘客的舒适性。
关键词:乘客-车辆-桥梁系统;耦合振动;乘车舒适性
中图分类号:U441.3;U448.25 文献标志码:A 文章编号:1004-4523(2018)01-0030-09
DOI:10.16385/i.cnki.issn.1004-4523.2018.01.004
引言
随着中国京沪、京福等高速铁路干线的不断开通运营,快捷便利的高铁成为广大乘客出行的理想选择。由于列车运行速度很快,且大多是在高架桥及大跨度桥梁上运行,轨道不平顺及轮对蛇行运动激发的车桥耦合振动,成为影响车辆运行平稳性及乘客乘车舒适性的主要因素,逐渐成为铁路部门普遍关注的焦点。
目前国内外关于铁路车辆运行平稳性的评价标准是以车辆的振动加速度作为评价旅客乘车舒适程度的主要依据。胡振东等以常量力匀速通过简支梁为研究对象,采用理论推导分析了车辆垂向加速度及其对车辆舒适性的影响。王贵春以大跨度公路斜拉桥为背景,计算了多辆汽车运行时车桥耦合振动状态,以车辆振动响应为依据,参考ISO2361-1-1997的规定,对乘车舒适性进行分析。韩万水等以汽车驾驶员位置处的振动响应作为依据,对风场中行驶在杭州湾跨海大桥上的汽车车辆驾驶舒适性进行了计算及评价。然而乘客与车体的振动之间存在一定的差异,现有铁路舒适性评价标准中缺乏对这一差异的考虑,因此有必要对乘客本身的振动响应进行研究,从而为改进高速铁路乘车舒适性提供依据。王英杰等将人体视为通过弹簧一阻尼装置连接于车厢底板的单自由度系统,建立人一车系统动力分析模型,比较了车辆及人体振动的差异,以人体振动响应为基础数据研究车辆行驶过程中乘客的舒适性问题。刘习军等建立了包括头部、脏腑和躯干及座椅组成的8个自由度人体模型,根据达朗贝尔原理推导系统的动力平衡方程,繪制了处于车厢不同位置乘客头部的加速度分布图,从而通过乘客的乘坐舒适性进行评价。Nishiyama建立了具有12个自由度的数学模型,其中车辆模型由3个质量单元组成,考虑其4个方向自由度,乘客模型由4个质量单元和铰接梁单元组成,考虑其6个方向自由度,大型车辆由弹簧质量组成,考虑2个自由度,对大型车辆引起的公路桥梁车辆及乘客的动力响应进行了计算。以上研究所建立的人体模型相对比较简单,但是却奠定了采用以乘客模型为研究对象从而进行舒适性评价的基础。
1乘客-车辆-桥梁耦合振动模型
为了更加细致地分析列车经过桥梁时系统各部分的振动状态,建立了如图1所示的由桥梁模型、车辆模型和多个乘客模型组成的耦合振动系统。
1.1车辆模型
每节车辆均是由车厢、转向架和轮对以及弹簧一阻尼系统组成的多自由度振动系统。以具有二系悬挂装置的客车车辆为例,假定车厢、转向架和轮对为刚体,即不考虑振动过程中的弹性变形,车厢和转向架之间通过二系悬挂装置进行连接,转向架与轮对之间通过一系悬挂装置进行连接,如图2所示。
1.2乘客模型
车厢内乘客假定为N排座席,将每排座椅上的乘客视为一组刚体,通过弹簧一阻尼装置与车辆进行连接,如图3所示。
1.3车辆-乘客耦合作用模型
根据拉格朗日运动方程推导车辆及乘客系统的运动方程
1.4桥梁模型
桥梁结构一般采用有限元软件进行建模,由于自由度很多,计算工作量巨大,为减少计算自由度,可以采用模态综合技术,利用振型正交性,把运动方程进行解耦,通过提取占主要控制作用的前几十阶频率和振型,即可对桥梁的整体振动进行分析,大大缩减计算工作量,提高计算效率。
桥梁任意截面的位移均可由以下振型函数进行叠加得到
若将桥梁振型进行规格化,其第m阶模态方程可以表示为
1.5车辆-桥梁耦合作用
将车辆与桥梁的运动方程进行联立可得
由式(20)~(22)可知,桥梁运动方程中的外力作用受车辆质量、轨道不平顺的影响,运动方程中的刚度矩阵和阻尼矩阵与车辆位移耦联,因此桥梁的运动状态受车辆运动影响。
由式(13)~(19)可知,车辆的运动方程中外力向量受轮对位移影响,而轮对位移又由其所在位置桥梁位移与轨道不平顺、轮对蛇行运动叠加而成;式(23)中车辆运动方程也与桥梁位移耦联,因此车辆的运动状态受桥梁的位移影响,形成了车桥耦合振动系统。
1.6乘客-车辆-桥梁系统运动方程
对方程(13),(23)进行联立,可得乘客一车辆一桥梁耦合系统的运动方程
对于以上时变系数的运动方程,可通过New-mark-β法进行积分迭代计算,采用Fortran编写相应计算程序,对列车匀速通过桥梁的过程中系统各部分的振动响应进行研究。
2计算实例
选取某(180+216+180)m的公铁两用长江大桥进行研究。主桁高度为16m,节间长度为9m,加劲拱与桁梁组成刚性桁梁柔性拱体系。其中,支点处加劲桁高16m,加劲拱矢高在两边跨为24m,主跨为32m。两主桁中心距12.5m,双线铁路布置于钢梁的下弦,中心间距4.2m,铁路明桥面,立面布置图如图4所示,横断面如图5所示。
采用有限元分析软件MIDAS建立的桥梁有限元模型如图6所示,其前30阶振动频率在0.47~2.96Hz范围内变化。由于大跨度桥梁的自振频率较低,振动主要由低频起控制作用,因此根据计算精度及收敛性要求,提取其前30阶振型进行耦合振动计算,将其中的前10阶自振频率及相应的振型特征描述列于表1。
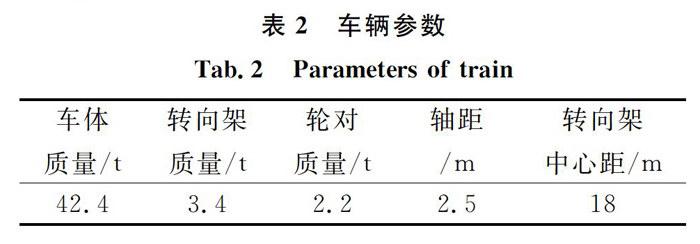
由于车辆及乘客的振动自由度相对较少,因此直接采用有限元进行计算,综合考虑所有频段的影响。车辆编组采用6节车輛组成的先锋号动车组进行计算,车辆主要技术参数如表2所示。每节车厢内考虑10排乘客,乘客参数如表3所示,列车运行速度取150km/h进行计算。
为更加明显地体现乘客模型对车桥耦合振动分析的影响,选取乘客一车辆一桥梁耦合振动模型及车辆一桥梁耦合振动模型分别编程进行计算。
将列车匀速在桥梁上行驶过程中,桥梁边跨及主跨跨中的竖向位移及横向位移时程曲线分别绘于图7和8,第3节车厢的竖向及横向加速度时程曲线绘于图9,车辆与乘客的位移、加速度时程曲线对比绘于图10和11。
由图7可以看出,考虑乘客与车辆间的耦合作用后,桥梁的边跨及主跨跨中位移时程曲线振动趋势没有发生任何变化,仅位移极值稍有增加,主跨跨中位移由1.59cm增加至1.69cm,边跨跨中位移由1.72cm增加至1.86cm,竖向位移最大变化幅值为8%。综合文献中的研究成果及本文中图7的曲线可知,桥梁的竖向位移主要由列车的重力加载引起,因此乘客及车辆的耦合振动对桥梁的竖向位移影响比较有限。
列车运行过程中引起的桥梁的横向振动主要来源于轨道不平顺及轮轨蛇行运动,但其数值通常比较小,一般在几毫米以内。但大跨度桥梁在风、地震、船舶撞击等外荷载作用下,桥梁的横向位移会大幅增加,增幅高达数十倍甚至上百倍。图8中两种模型计算所得桥梁横向位移时程曲线差别比较明显,但是由于振动幅值较小,因此在没有外荷载作用时,由于考虑乘客模型所引起的桥梁横向位移变化也可忽略。
由图9可以看出,两种计算模型所得车辆的竖向及横向加速度时程曲线变化趋势基本保持一致,但是考虑乘客与车辆的动力相互作用后,车辆的振动幅值有明显增加,车-桥模型计算所得车辆竖向加速度极值为10.76cm/s2,横向加速度极值为41.59cm/s2;而考虑乘客模型后,车辆的竖向加速度极值增加到15.06cm/s2,横向加速度极值增加到43.07cm/s2。在乘车舒适性评价时通常会取各向加速度的均方根,因此综合考虑后,乘客对车辆的动力作用影响不容忽视。
由图10及11可以看出,乘客与车辆的振动位移及加速度变化趋势基本保持一致,但是乘客的振动明显存在一定的滞后,乘客竖向位移极值为1.45cm,横向位移极值为0.11cm,转角位移极值为2.3×10-3,竖向振动加速度幅值为15.57cm/s2,横向振动加速度幅值为46.63cm/s2,明显较车辆的振幅偏大,与实际工程中的行车状态保持一致。
将车上的10排乘客横向及竖向振动加速度频谱绘于图12。由图中可以看出,乘客的振动频率基本集中在1~4Hz范围内,对于低频振动比较敏感。横向振动频谱在3Hz处有明显波峰,且横向振动更容易引起乘客的不适,该计算结果与文献的研究结论保持一致,因此在进行车辆及其内部座椅设计时应尽量避开该频段,以提高乘车舒适性。
3结论
通过拉格朗日方程建立乘客一车辆一桥梁耦合振动模型,编程计算了乘客、车辆、桥梁的振动响应,并与车辆一桥梁模型计算所得结果进行了对比,得出结论如下:
(1)是否考虑乘客模型对于桥梁的位移计算影响不大,因此在桥梁结构设计时,仅考虑车辆对桥梁的激扰作用即可,车上乘客影响可以忽略;
(2)乘客模型对于车辆的动力响应极值存在明显影响,因此要准确地模拟车辆的运动状态,应综合考虑乘客、车辆及桥梁之间的耦合动力作用;
(3)乘客的振动状态与车辆存在明显区别,且振动幅值较车辆偏大,因此传统的采用车辆的振动响应对乘车舒适性进行评价的方法可能会过高地估计乘客的舒适性。若对乘车舒适性进行评价需要建立更加细致的乘客-车辆-桥梁耦合振动模型才能得到更加准确的结论。