颗粒粒径对流态化两相流动影响的数值计算研究
2018-04-10陈震芳
李 麟,陆 梁,孙 磊,崔 尧,陈震芳
(1.上海电力建设启动调整试验所,上海 200093;2.上海上电电力工程有限公司,上海 200090;3.上海发电设备成套设计研究院有限公司,上海 200240)
流态化现象是指固体颗粒在流体(气体或液体)的作用下悬浮在流体中跳动或随流体流动的现象[1]。运用该原理的气固流化床是能源、化工、石油、冶金行业中的重要设备[2]。近年来,随着流态化技术的发展,微颗粒流态化在煤粉流态化燃烧、物料干燥等诸多领域的应用越来越广泛。以FLUENT为数值计算工具采用欧拉双流体模型,对不同颗粒粒径在流化床模型内的流态化情况进行模拟研究。
1 数值模拟方法
1.1 数值计算理论
气固两相流CFD的模拟方法通常有欧拉-拉格朗日方法和欧拉-欧拉方法[3]。采用欧拉-欧拉方法进行研究,将假定流体相和固体相均为连续,可以相互穿透的流体。流体与固体相均以体积分率进行表示,固体颗粒间相互作用采用颗粒动力学的方法,气固间动量交换采用经验性曳力模型进行描述。以下为该次模拟中采用的欧拉-欧拉方法的控制方程组:
εg+εp=1
(1)
式中εg和εp——表示气相和固相体积分率。

(2)

(3)

(4)
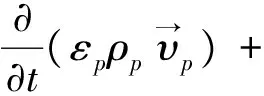
(5)
式(1)、(3)和式(2)、(4)为分别气相和固相的质量守恒方程和动量守恒方程。其中,σ为雷诺应力;g为重力加速度;-αp表示两相间的相互作用力(曳力和浮力)[4]。本次模拟中采用的Gidaspow模型曳力系数[5]定义如下:
(6)
(7)
式中CD0——单颗粒曳力系数。
气相湍流输运方程采用k-ε双方程模型[6]:
(8)
(9)
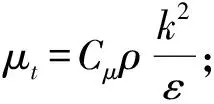
1.2 数值网格和计算设置
数值计算采用了宽度为0.186 m,高度为1.600 m的流化床模型。其计算网格和边界设置如图1所示。

图1 计算网格和边界设置
该套网格有88 911个运算节点,计算模型下端设置为速度进口,其采用自定义函数定义进口速度为抛物线分布,其中心最大处速度大小是1.0 m/s,近壁面处速度为0.5 m/s,出口压力为标准大气压力,其他壁面均为标准壁面。流态化过程不考虑传热,化学反应等过程的作用。静止床层的高度为0.382 m,固相体积分率考虑颗粒粒径因素在0.56~0.85范围内选取。
数值模拟过程采用欧拉两相流模型,将颗粒作为拟流体进行近似处理,选取k-e模型,曳力模型为Gidaspow模型,颗粒碰撞还原系数为0.9。计算时初定时间步长为0.000 5 s。
粒径参考照Geldart[7]理论进行选取,如表1所示。

表1 数值模拟参数设置
本模拟计算主要是在其他条件保持适当值时,通过不断改变颗粒粒径来进行比较分析,根据床内固相体积分率随时间的变化来分析其流态化特性的异同。
2 模拟结果与分析
颗粒粒径为500、50、5 μm以及0.4 μm的流化床内固相体积分率随时间变化规律如图2~图5所示。

图2 流化床内固相体积分率随时间变化规律(颗粒粒径500 μm)
由图2可以看出,在0 s时,没有气流进入,静止床层高度为0.382 m,流化床中处于静止状态。在0.1 s处,有速度呈类抛物线分布的气流通过进气口进入床层,颗粒在气流的作用下上移一小段距离后在底部产生小气泡;在0.3 s处,气泡逐渐长大,并在底部再次产生了两个近似对称的小气泡;在0.5 s时,最初产生的气泡不断长大并产生不规则运动;在0.6 s,0.7 s时,大气泡运动到静止床层的顶部,开始破裂。在1 s时,大气泡破裂,第二层两个气泡继续向上,床的底部不断产生新的气泡群。1.5 s处,底部开始产生不规则的气泡运动,此后,颗粒在床体内翻腾流化。由图3至图5可知,颗粒粒径D=50 μm、D=5 μm以及D=0.4 μm的流态化情况初期基本与颗粒粒径D=500 μm时的情况基本一致,但是在气泡尺寸和形状方面有一定的差异。在开始形成流态化(1.5 s)后,D=50 μm、D=5 μm颗粒粒径的算例中,流化床上部位置也出现固相分布,即其在顶部固体颗粒在气流的携带上进入上部并进行翻腾并最终流出反应区域。而D=0.4 μm颗粒粒径的算例中,气泡形成后并没有明显的破裂阶段,而是和周围固相不断融合。这与纳米级颗粒粒度可能会出现的颗粒凝聚[8]有一定的关系。而后由于颗粒粒径过小,大部分颗粒被吹出了反应器。

图3 流化床内固相体积分率随时间变化规律(颗粒粒径50 μm)
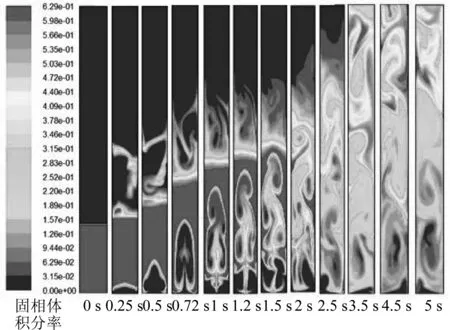
图4 流化床内固相体积分率随时间变化规律(颗粒粒径5 μm)

图5 流化床内固相体积分率随时间变化规律(颗粒粒径0.4 μm)
3 结语
(1)随着颗粒直径的逐渐减小,固含率的增加,气泡成长过程的时间逐渐增加。产生的气泡性质也开始发生变化,颗粒细化到一定程度后,气泡在成长过程中,与周围进行较为明显的物质交换。
(2)颗粒直径减小到一定程度后,床内会出现大气泡未脱落,小气泡不断产生并不断融入大气泡的现象。与此同时,大气泡以较快的速度与外部进行物质交换,最终大气泡会布满整个床体并吹出床体。
参考文献:
[1]吴占松, 马润田, 汪展文. 流态化技术基础及应用: “研究生教育创新工程”化工类研究生教学用书[M]. 北京:化学工业出版社, 2006.
[2]金涌 等. 流态化工程原理[M]. 北京:清华大学出版社.
[3]王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京:清华大学出版社, 2004.
[4]TAGHIPOUR F, ELLIS N, WONG C. Experimental and computational study of gas-solid fluidized bed hydrodynamics[J]. Chemical Engineering Science, 2005, 60(24): 6857-6867.
[5]SINCLAIR J L. Multiphase flow and fluidization: Continuum and kinetic theory descriptions[J]. PowderTechnology, 1995(3): 287.
[6]FLUENT I. Fluent 5 User′s guide[J]. Fluent Inc, 1998, 2:8-12.
[7]GELDART D. Types of gas fluidization[J]. Powder Technology, 1973, 7(5): 285-292.
[8]孙玉绣, 张大伟, 金政伟. 纳米材料的制备方法及其应用[M]. 北京:中国纺织出版社, 2010.
