问题引导下的变式策略在习题教学中的应用——以“水平面内的圆周运动”为例

(江苏省海门实验学校，江苏　海门　226100)

1　问题的提出

习题教学是高中物理课堂教学中的重要组成部分，但在教学中发现，常有学生处于“听得懂，不会做”的状态，如何改变这一现象、实现学生能力的提升？马赫穆托夫的“问题教学论”认为：人们在认识活动中，当遇到现有条件或已有的经验尚无法解决的实际问题时，就会产生一种怀疑、探索的心理状态，从而激活主体思维，试图去找出解决问题的办法。[1]基于以上原理形成的问题引导下的变式教学策略，以问题引导为教师“导”的方式，通过设置变式问题，让学生在体验中获取知识，在比较中感悟差异与方法，在归纳总结中提升能力。笔者认为，此教学方法可在习题教学中进行有益的尝试。

2　问题引导下的变式教学策略

问题引导下的变式教学策略，就是指依据教学目标和学生现有的知识储备、解决问题的实际能力，教师从一个基本的、典型的问题入手，通过多层次、多角度的变式问题，形成一组有梯度、有中心、有序列的问题组，让学生经过充分思考，去辨析、提炼，从而丰富知识储备、强化对过程与方法的把握、升华其解决问题的能力。问题引导下的变式教学要为学生留足“空白”，为学生提供表述、质疑、探讨问题的机会，同时要将教学活动改造为宽松、和谐的师生探讨交流的过程，[2]只有如此，学生才能真正在和谐的氛围下全身心投入到学习中去，改“被动听讲”为“主动参与”，实现思维的飞跃。

问题引导下的变式教学策略在具体实施中可将整个过程分为三个环节：基准问题——多层次变式问题探究——比较提炼。从变化的形式上看，可以有“变设问”“变研究对象”和“变条件”等多种方式，下文将结合实例加以阐明。

3　问题引导下的变式策略的应用

“水平面上的圆周运动”是中学物理中的一类典型运动问题，对该类问题的分析，有助于学生掌握圆周运动的处理方法，以及为后面“竖直平面内的圆周运动”的分析奠定基础。

3.1　基准问题

如图1所示，有一水平放置的圆盘，上面有一个质量为m=2kg的小物块，该物块离圆盘中心轴的距离为r=0.2m，求：

(1) 圆盘带动小物块在水平面上转动时，线速度的大小为0.5m/s,则该物块的角速度多大？在此种情况下，圆盘给物块的摩擦力多大？

(2) 若圆盘与物块间的fm=10N,且物块始终随圆盘一起做匀速圆周运动,则圆盘所允许的最大转速是多大?

图1

设计理由：基准问题通常是由教师依据本节课的教学要求和学生的实际水平，精选一道具有基础性、典型性、可变性的物理问题，将其作为变式教学的基准点。为了使课堂教学能够顺利进行，保护学生学习的积极性和调动课堂氛围，该题是本类问题的典型问题，要求能够应用基本知识和常规方法解决，且思维量要略小点。

3.2　变式问题

3.2.1变设问

变式1：如图2所示，三个由同种材料制成的物体放置在同一个水平圆盘上，三个物体的质量关系为m1∶m2∶m3=2∶1∶1，三个物体离中心轴的距离为r1=r2=r，r3=2r。

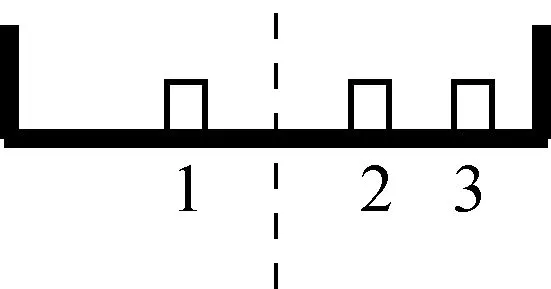
图2

(1) 当水平圆盘带动三个物体一起转动时,请分析哪个物体的向心加速度最大？哪个物体受到的静摩擦力最大？

(2) 三个物体中，哪个物体先与圆盘发生相对滑动？

设计理由：本题是“基准题”的第2和第3小问的综合，是“基准题”的一个纵向延伸，通过该题，可以进一步总结“水平面上的圆周运动”处理的一般方法，明确临界条件。

3.2.2变研究对象

变式2：如图3所示，在光滑的水平圆盘上放着一质量为1.2kg的小物块A，在地面上放置着另一个质量为0.6kg的小物块B，两物块用轻质绳相连，所有接触处均光滑。开始时，轻质绳刚好伸直，物块A与圆孔O的距离为0.2m，现使A以某一角速度绕中心轴线转动，若要求B不会与地面分离，则角速度ω的范围如何？

图3

设计理由：本题与前面两题相比，研究对象从“单体”到“多体”，主要考查了连接体问题在圆周运动情景下的应用中。要求学生通过本题的分析，能够明确：“几个物体运动状态不一致时，一般应采用隔离法”。另一方面，该题再次强化了临界问题的处理方法。

3.2.3变条件

变式3：若将“变式2”中的条件略做改变，如“A与圆盘间的fmax=3N，B物块被轻质绳悬挂于空中，要使A随圆盘一起绕中心轴转动而不发生相对滑动，则ω需要满足什么条件？”

设计理由：通过对条件的不断变化，让学生在新的问题情景中研读题意，思考问题解决的方法，加深学生对知识的理解。在比较中，让学生体悟到：问题情景变了，但处理的方法、问题的本质没有发生变化；在变化中，拓宽了学生的思路，提高了学生解决问题的能力。

3.2.4变连接装置

变式4：如图4所示为一水平面的俯视图，质量相同的两个物体P、Q分别固定在轻杆上，两物体到圆心的距离之比为1∶2，当整个装置在光滑水平面上绕圆心匀速转动时，杆OP段与PQ段对物体的拉力之比为多少？

图4

设计理由：从“线模型”到“杆模型”的转变，连接物所受作用力的特点发生了变化，此时必须思考、辨析其作用力的特点，结合状态分析力的特点。在实际处理中，如若学生对线、杆模型的作用力的特点存在疑问，教师还可以借用学生手边的物品，如胶带、笔等，构造“线球模型”和“杆球模型”，让学生加以体会。

3.3　比较提炼环节

通过上述一系列的变式问题，在培养学生发散思维的同时，还应注意“收敛、归一”，以形成良好的知识结构，深化对思想方法的认识。[3]因此，在课堂的结尾处，我们还设置了“比较提炼”环节，要求学生通过讨论，进行总结：① 圆周运动的一般处理方法——三部曲，即确定轨道平面、圆心和半径，对物体进行受力分析，明确哪些力提供了向心力；② 掌握多物体问题中“整体法”和“隔离法”选用的依据；③ 学会运用“极限法”处理临界问题；④ 体悟“线球模型”和“杆球模型”的不同特点。

4　教学反思

问题引导下的变式教学追求的目标是：通过改变物理问题的已知条件、研究对象、结论或设问等，让学生体悟到“变中有不变”，即在纷繁的变化中，不变的是物理本质，从而在一定程度上提高了学生的解题能力；通过引导学生总结和反思，可以排除相关干扰项，理清处理问题的思路，发现一些共性的方法；通过合作交流、表述观点等，可进一步提升学生的协作、表述、分析和综合等能力。

当然，在习题变式中还应注意两个关键点：① 变式的目的是为了提升学生的审题、分析等能力，强化学生对物理问题解决方法的掌握。因此，在变式时，应紧扣教学目标，不能为变而变。② 及时反思、比较和总结，“基准题”和“变式题”之间可能存在“形同质异”或“形异质同”的情况，在变式教学中，可以通过问题的引导，让学生及时地反思和比较，从而避免学生对问题的认知出现混乱。

参考文献：

[1] 鄢红春,李定国.问题链教学模式及其在物理教学中的应用[J].物理与工程，2011,(2)：54-56.

[2] 汤家合.高中物理习题教学实施变式探究教学模式初探[J].教学月刊，2011,(10)：9-12.

[3] 朱广科.基于本原性问题数学变式教学模式的研究[J].中学数学月刊，2016,(7)：12-14.