轴线角误差的斜齿轮拓扑修形及仿真*
2018-04-10张西金候祥颖
张西金,贾 超,候祥颖,郭 芳,翟 佳
(西北工业大学 机电学院,西安 710072)
斜齿轮具有重合度大,承载能力强等特点,在工业领域有广泛的应用.齿轮制造及安装误差不可避免,斜齿轮制造及安装误差会造成齿轮副轴线不平行,出现的轴线角误差会使其传动性能变差,而齿轮修形可以改善其传动性能[1-2].因此,可以通过斜齿轮修形技术研究,以便减少轴线角误差给其传动性能带来的不利影响.
近年来,斜齿轮修形研究取得了一些进展.文献[3]提出一种新的拓扑修形齿面,采用齿轮接触分析(Tooth Contact Analysis,TCA)技术进行了接触路径和传动误差分析,并应用有限元接触分析方法研究了轮齿弯曲应力和接触应力,但尚未研究修形齿轮的承载传动误差(Loaded Transmission Errors,LTE)情况.文献[2,4]推导了修形斜齿轮的齿面接触与边缘接触的全部计算,探讨了齿面修形对改善齿轮传动性能的作用,并在TCA基础上提出了一种斜齿轮承载接触分析(Loaded Tooth Contact Analysis,LTCA)(有限元方法和非线性数学规划方法的LTCA),对修形斜齿轮进行了LTCA计算,探讨了刀具修形及CNC机床修形两种方法,对其他修形方法未做探讨.文献[5]研究了沿齿廓方向抛物线修形的齿面结构,未涉及齿向修形.文献[6-7]通过理论齿面叠加修形齿面,基于TCA和LTCA,建立动力学模型,通过三维修形完成了宽斜齿轮多目标齿面优化,他也进行了斜齿轮对角修形多目标优化设计以减小振动与噪音,但都只进行了标准安装齿轮副的修形优化.目前国内外斜齿轮修形技术研究还不成熟,只有针对特定工况进行拓扑修形才能获得较好的传动性能,因此斜齿轮修形方法还需要探索完善.
文中针对轴线角误差的斜齿轮拓扑修形技术进行仿真研究,以减小轴线角误差对其承载传动误差(LTE)的影响,为斜齿轮修形设计提供了参考.
1 轴线角误差的斜齿轮拓扑修形
斜齿轮拓扑修形包括齿廓修形和齿向修形,齿廓修形是通过改变齿轮刀具切削刃的方法实现的,齿向修形是通过数控机床的多轴联动实现的,这样的修形方案可以提高修形效率.对于加工刀具齿条(滚刀),可以将直线齿廓改变为圆弧形、抛物线形等形式,由于圆弧齿廓修形研究较少,所以这里研究圆弧形齿廓修形,也就是在法平面内刀具齿廓为圆弧形.为了减少修形工作量,采用小轮修形,大轮为标准渐开线齿轮的方案.建立如图1所示的动坐标系Sc10和Sc1,它们都固定在小轮的加工刀具齿条上,Xc10Yc10为齿条齿宽中心处的法平面,采用圆弧形齿廓(如图1所示),其中R为圆弧半径,R越大修形量越大;圆弧与原来的直线齿廓相切,切点距离节线与直线齿廓的交点为c,节线上下工作齿面的修形量应该有所不同,设置参数c的目的就是为了减小靠近齿根部位工作齿面的修形量而增大靠近齿顶部位工作齿面的修形量;a表示节线上法向半齿厚.
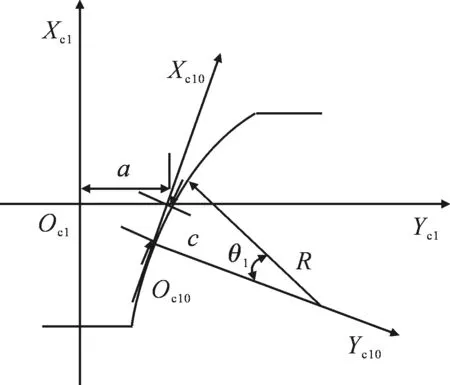
图1 修形刀具齿形
在圆弧形齿廓刀具展成加工齿轮的基础上,齿向采用鼓形修形,中间段采用直线,两侧采用曲线,研究表明高阶修形具有较好的传动性能,这里采用四阶修形曲线.考虑轴线角误差的影响,两侧的修形情况应该有所不同,即采用不对称的齿向修形方案.齿向修形如图2所示.

图2 齿向鼓形修形
在Sc10坐标系中刀具齿面的四元位矢γc10表示为
(1)
式中:u1为Xc10坐标值,v1为Zc10坐标值.
齿向修形公式为
(2)
将γc10变换到Sc1坐标系中需要经过四次坐标变换,每次的转换矩阵可以由以下公式得出[8]:

最终的变换矩阵如下:
式中:α为压力角;β为螺旋角.在Sc1坐标系中齿条齿面的四元位矢和单位法矢表示为:
rc1=Dc1c10rc10
(3)
(4)
式(3)和式(4)完全表达了齿条刀具的空间曲面情况,刀具齿面在加工齿轮时按展成原理就可以加工出齿轮齿面,由于刀具齿廓已不再是直线形式,因此加工出来的齿轮齿廓也不再是标准的渐开线齿廓.
2 拓扑修形斜齿轮齿面接触分析
2.1 修形齿面建模
拓扑修形齿面建立采用了通过理论齿面与法向修形曲面叠加构造修形齿面的方法[6],理论齿面采用刀具展成加工形成的曲面,而法向修形曲面是考虑齿向鼓形修形产生的修形曲面,法向修形量为式(2)所示.建立如图3所示的展成加工坐标系,Sa1为固定坐标系,S1为小齿轮的动坐标系,Za1和Z1都是和齿轮的回转中心重合.S1随小齿轮一起绕Za1轴转动,刀具沿Yc1轴平移,刀具齿面展成过程中形成齿轮齿面,因此小齿轮齿面位矢和单位法矢可以表示为
r1=M(φ1)1c1rc1
(5)
n1=M(φ1)1c1nc1
(6)
其中M(φ1)1c1是刀具坐标系Sc1到小轮坐标系S1的转换矩阵,展成过程中满足关系式H=Rp1×φ1,Rp1为节圆半径,H为位移,φ1为齿轮转角.
根据微分几何中的啮合方程可以得出以下关系
(7)
将式(7)代入式(5)和式(6)可以确定小轮理论齿面情况,也就是可以得到刀具齿面上任何一点在小齿轮齿面上的对应点.
实际小轮齿面是由理论面与法向修形曲面叠加形成的,其位矢和法矢[6]为
r1r=δ(u1,v1)n1+r1
(8)
(9)
大轮采用标准齿条刀具展成加工,齿面建模过程在这里不再累述.

图3 齿轮展成示意图
2.2 齿面分析
轮齿承载接触分析技术是在载荷作用下对齿轮的啮合过程进行高精度的计算机仿真,以获得设计齿轮在拟真实工况条件下的工作性能的一个重要手段,LTCA计算得到承载传动误差是分析齿轮动态性能(振动、噪声)的一个参数,LTE波动越小齿轮啮合动态性能一般越好.这里采用LTCA进行斜齿轮拓扑修形分析,而LTCA是建立在TCA基础上的,因此需要同时研究TCA技术.
建立如图4所示的TCA分析坐标系,Sa1和Sa2是辅助坐标系,不随齿轮转动且互相平行,用于表示轴线角误差.其中固定坐标系Ss的Zs轴与大轮的回转轴重合.在固定坐标系中,大小轮配对齿面在啮合传动时啮合点位矢及单位法矢必定相同,由此可得到如下TCA分析方程.
M(φ1,γ1,γ2)s1φ=M(φ2)s2r2
(10)
M(φ1,γ1,γ2)s1φ=M(φ2)s2n2
(11)
式(10)~(11)中M(φ1,γ1,γ2)s1和M(φ2)s2分别表示小轮和大轮坐标系到固定坐标系的变换矩阵,φ1和φ2是大小轮的瞬时转角,γ1和γ2是不同方向的轴线角误差.由于n1r和n2为单位法矢,所以构成了5个独立方程,结合大小轮展成过程中的啮合方程可以得到啮合点.进一步可以获得各接触椭圆的长轴及齿面间隙.
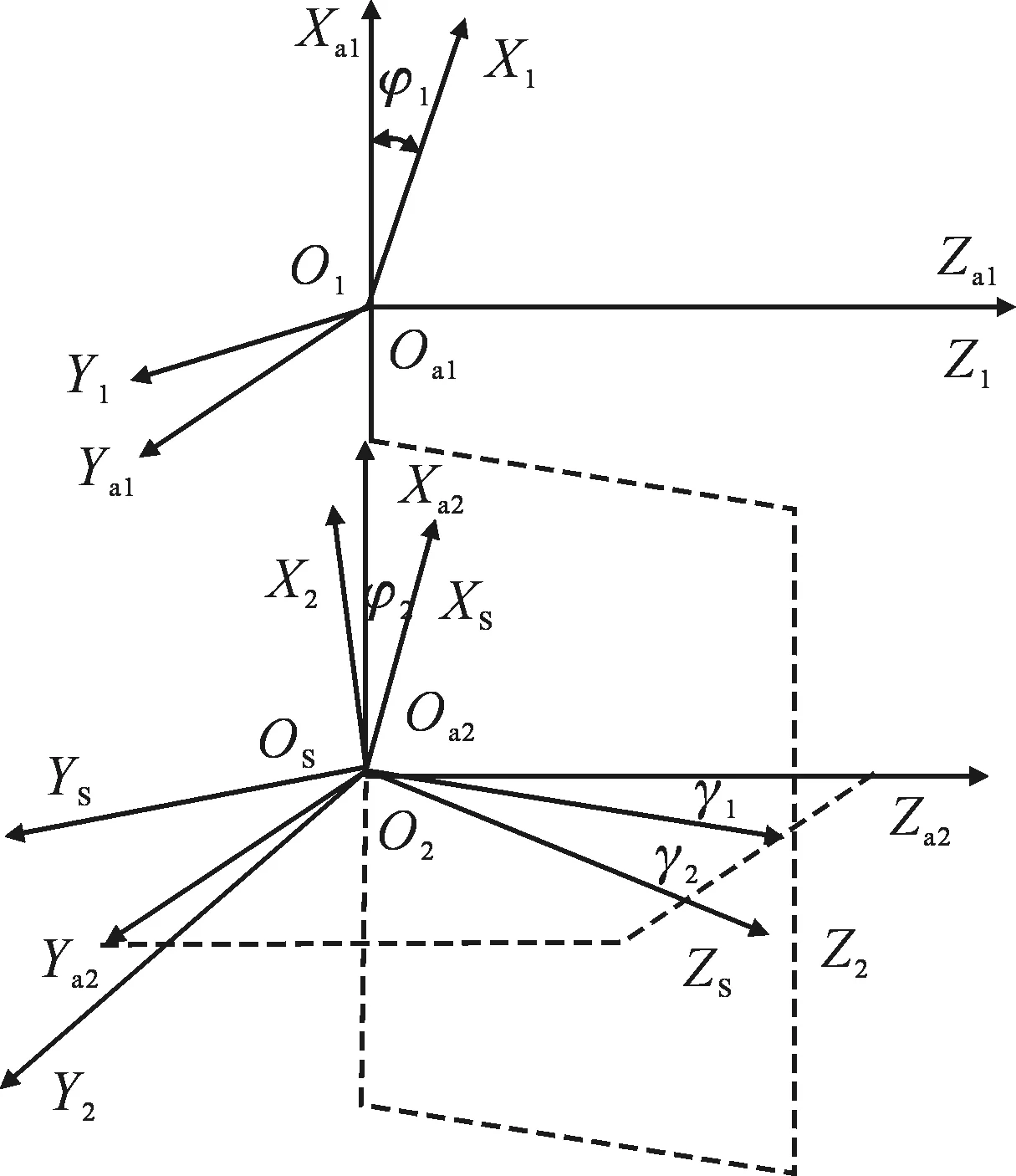
图4 TCA坐标系
式(12)中F为接触轮齿的法向柔度矩阵;P为传递力矩计算得到的齿面法向力;p和d分别为齿对沿接触椭圆长轴离散点构成的法向载荷向量及变形后的齿面间隙向量,w为沿接触椭圆长轴离散点变形前的齿面间隙向量,Z为轮齿的法向位移向量,pj和dj为沿接触椭圆长轴的离散法向载荷及变形后的齿面间隙.
在TCA基础上进行承载接触(LTCA)分析,接触分析方程为
(12)
在此基础上可以得到承载接触分析数学规划模型[9],F采用有限元计算获得,w由TCA计算获得,P由传递力矩计算得到,由此求解承载接触分析数学规划模型获得参数p、d、Z.将Z转化为大轮转角,即可得到承载传动误差.
3 斜齿轮齿廓修形参数
斜齿轮齿廓拓扑修形包括齿廓修形和齿向修形,首先研究齿廓修形问题.齿轮的基本参数为:小轮齿数30,大轮齿数45,法面模数6,压力角20°,螺旋角15°,传递力矩750 N·m-1.设计圆弧半径R=K1×mn,mn为法向模数,为了不影响接触强度,圆弧半径不应太小.设计c=K2×mn,其中K2=0时圆弧齿廓切点在齿条刀具节线位置,K2越大表示圆弧齿廓切点离齿条刀具节线越远.
通过仿真发现:当圆弧半径R过小时会产生齿侧边缘接触,而且传动误差和齿面接触应力都比较大;当圆弧半径R太大时,齿廓修形量太小时,又会造成齿顶边缘接触.综合考虑取R=250mn,且取c=0,使鼓形中间区的大小轮啮合点都在分度圆上.
4 轴线角误差的斜齿轮齿向修形
实际齿轮安装时一般都会存在轴线角误差,由于不同轴线角误差需要的修形是不同的,所以需要研究不同轴线角误差下的不对称的修形问题,以便齿轮副在实际安装工况下取得较好的传动性能.鉴于齿向修形参数对承载传动误差影响较大,所以这里齿廓修形参数取前面的值,只研究齿向修形的修形量和修形长度对传动误差的影响,从而确定合理的修形参数.
对于高精度齿轮ISO推荐齿向鼓形最大修形量为:10~25 μm,这里我们取最大修形量为10 μm和25 μm两种情况进行研究.
4.1 轴线角误差γ1的修形
以Ya2Za2投影面内轴线角误差γ1取0.05′为例,b为齿宽,左右两端最大修形长度分别取0.1b、0.2b、0.3b、0.4b和0.5b,左右两端最大修形量分别取(δLmax=0.010 mm,δRmax=0.010 mm)、(δvLmax=0.025 mm,δRmax=0.025 mm)、(δLmax=0.010 mm,δRmax=0.025 mm)和(δLmax=0.025 mm,δRmax=0.010 mm)四种情况进行LTCA仿真,其中一种情况的仿真结果如图5所示,四种情况的最小传动误差波动见表1.
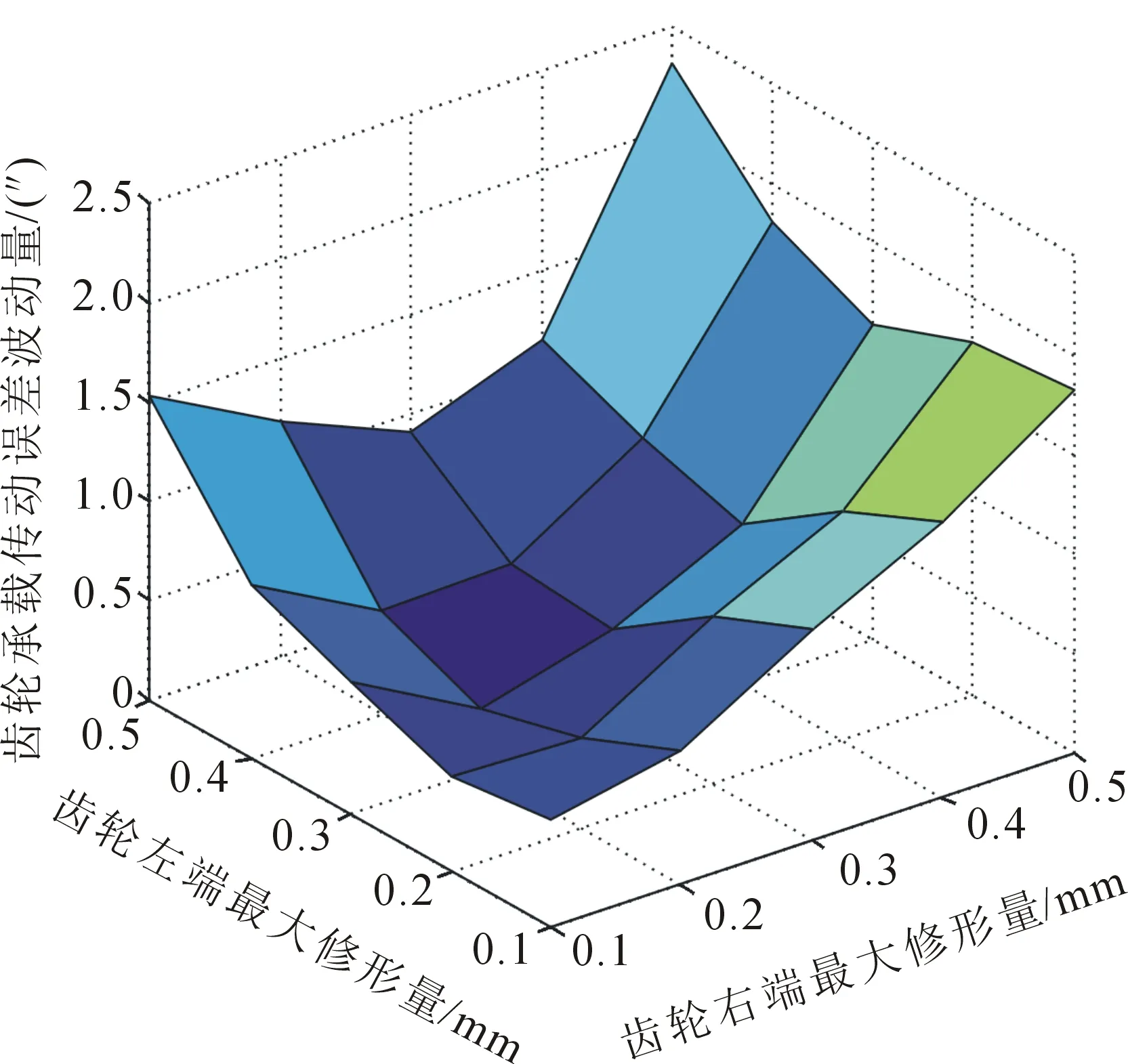
图5 轴线角误差γ1为0.05′时LTE波动量(δLmax =0.010,δRmax =0.025)
从图5可以看出,TLE波动量随最大修形长度及最大修形量变化关系比较复杂,但左右最大修形长度都为0.5b时TLE波动量最大,这是最不利的传动情况.
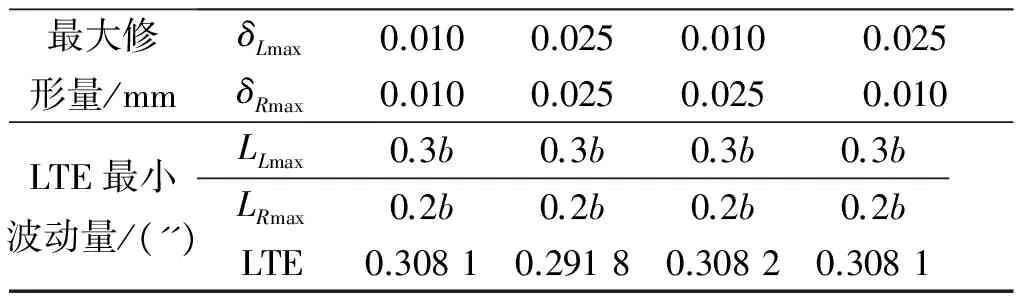
表1 γ1为0.05′时LTE波动量
从表1可以看出,四种情况所对应的最小LTE波动量相差很小,最小LTE波动量对应的最大修形长度相同(左端最大修形长度0.3b、右端最大修形长度0.2b),说明取最大修形长度不对称的设计可以取得最好的传动性能.
根据表1确定合理的修形参数为:左端最大修形长度0.3b、右端最大修形长度0.2b、左右两端最大修形量均为0.025 mm,此时承载传动误差最大波动量为0.291 8,与未修形相比承载传动误差最大波动量减少了42.85%(未修形时LTE最大波动量为0.510 6),修形结果表明该修形方案可以提高传动性能.该组参数仿真得到传动误差及载荷分配系数如图6所示,从图6中可以看出LTE波动小,主要承载区域在齿面中间,两侧区域没有承载,说明还有富裕的承载能力,可以传递更大的力矩.
4.2 轴线角误差γ2的修形
以Xa2Za2投影面内轴线角误差γ2取0.05′为例,左右两端最大修形长度分别取0.1b、0.2b、0.3b、0.4b和0.5b,左右两端最大修形量同样采用情况进行LTCA仿真,其中一种情况的仿真结果如图7所示,四种情况的最小传动误差波动见表2.
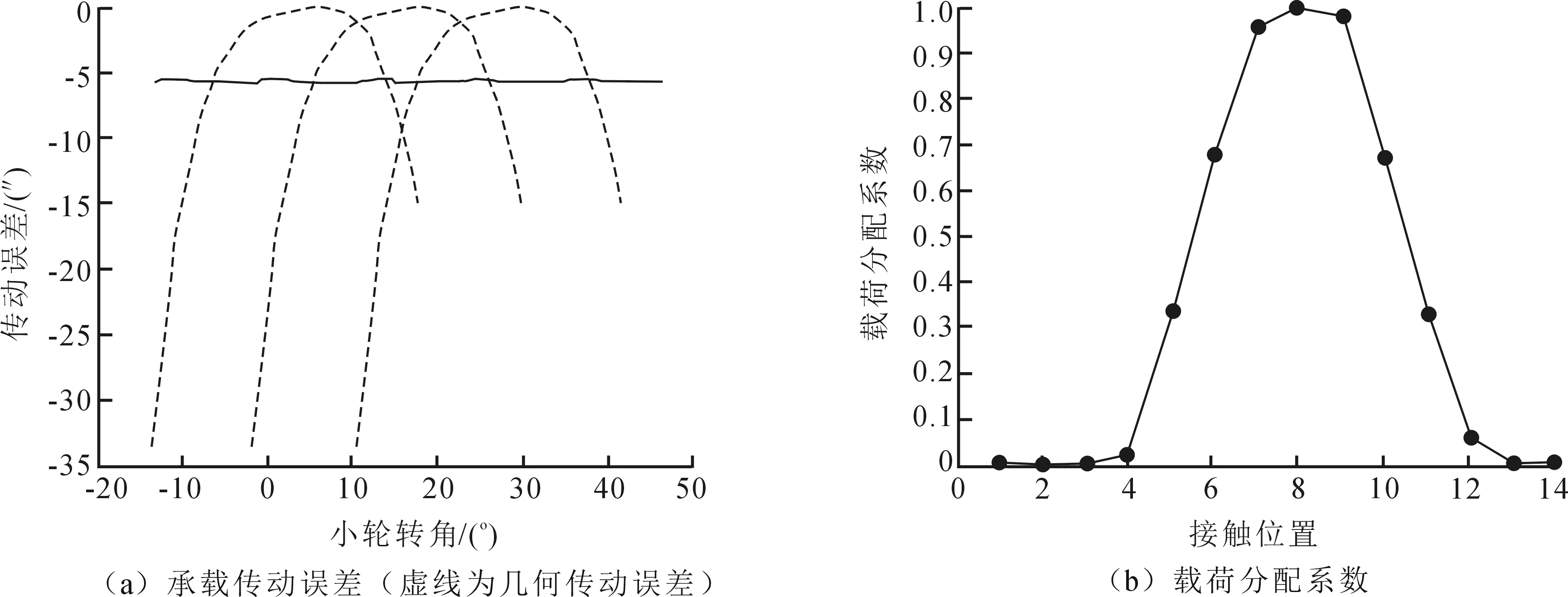
图6 轴线角误差γ1为0.05′时齿轮啮合性能
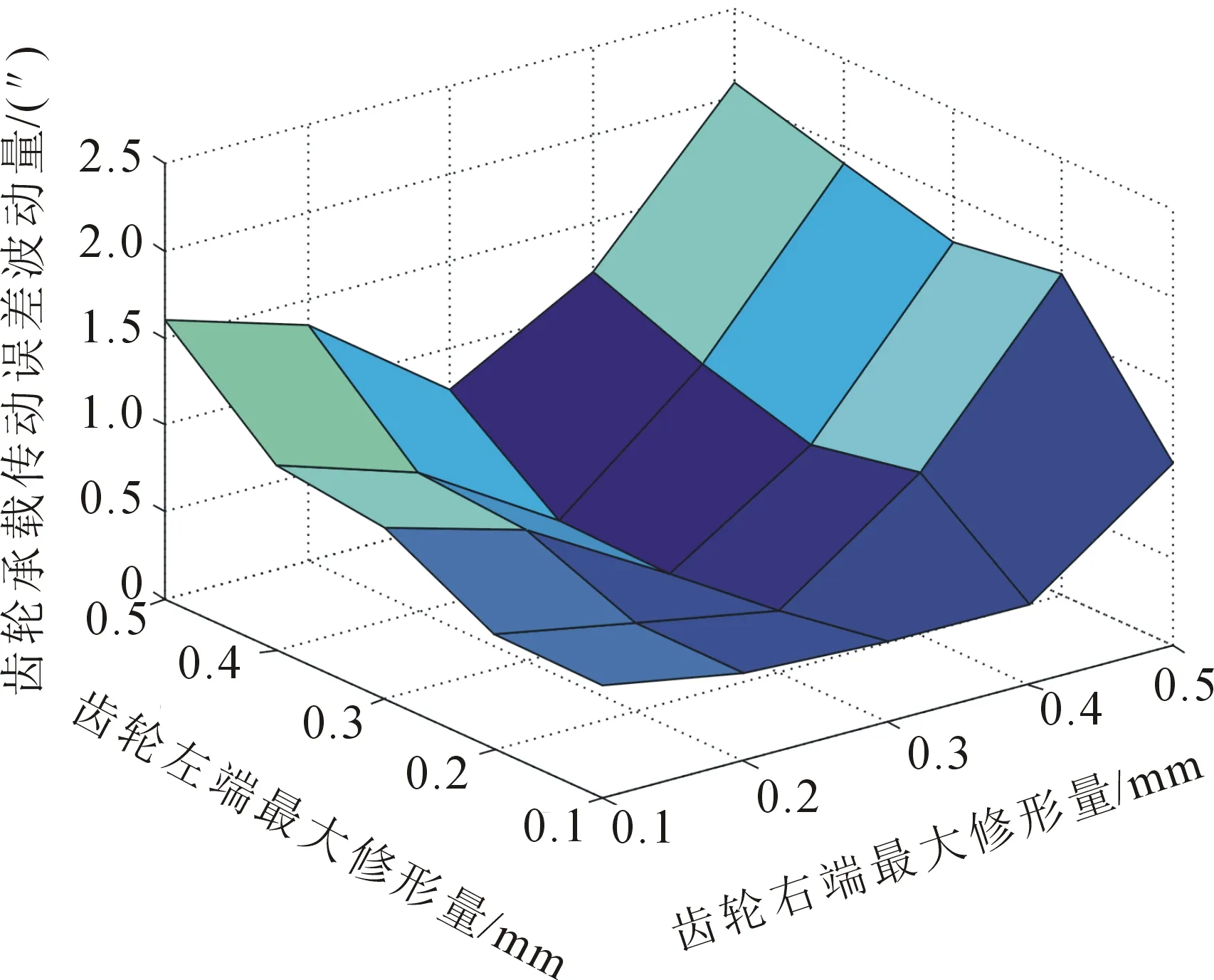
图7 轴线角误差γ2为0.05′时LTE波动量
从图7可以看出,TLE波动量随最大修形长度及最大修形量变化关系比较复杂,但左右修形长度都为0.5b时TLE波动量最大,这是最不利的传动情况.从表2可以看出,四种情况所对应的最小LTE波动量各不相同,取最大修形量不对称(左端最大修形量0.010 mm、右端最大修形量0.025 mm)的设计可以取得最好的传动性能.
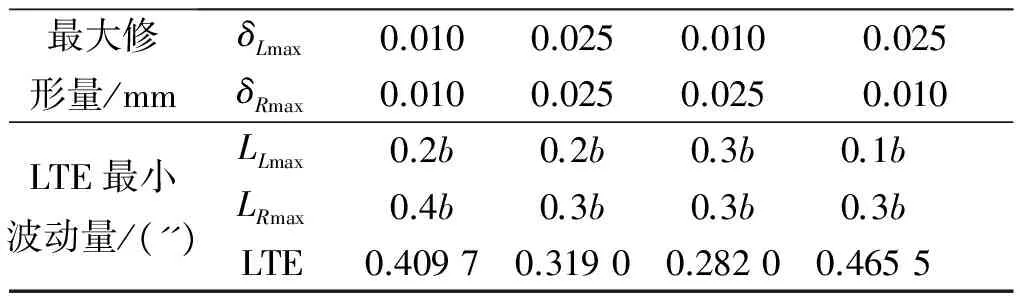
表2 γ2为0.05′时LTE波动量
根据表2确定合理的修形参数为:左右两端最大修形长度均为0.3b、左端最大修形量0.010 mm、右端最大修形量0.025 mm,此时承载传动误差最大波动量为0.282 0,与未修形相比承载传动误差最大波动量减少了53.47%(未修形时LTE最大波动量为0.606 1),修形结果表明该修形方案可以提高传动性能.该组参数仿真得到传动误差及载荷分配系数如图8所示.从图8可以看出LTE波动小,主要承载区域在齿面中间,两侧区域没有承载,可以传递更大的力矩.
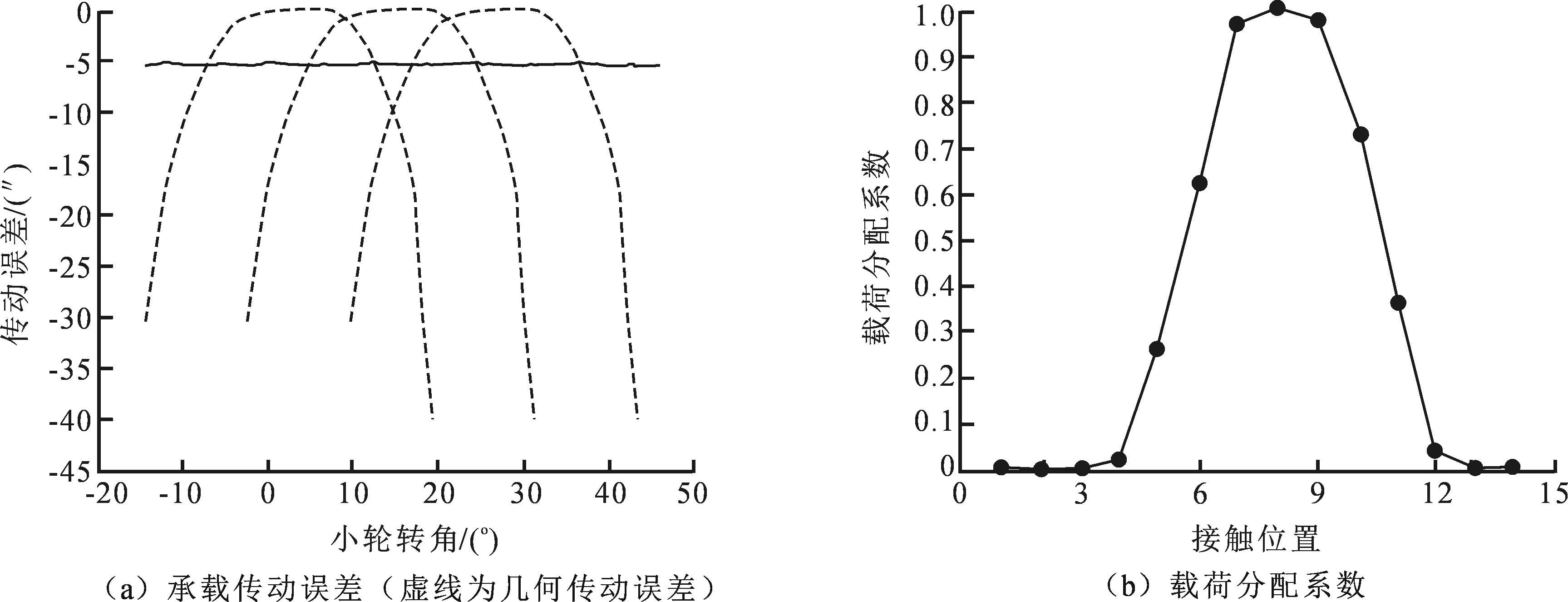
图8 轴线角误差γ2为0.05′时啮合性能
5 结 论
1) 提出了轴线角误差的斜齿轮拓扑修形新方案,用圆弧齿廓刀具展成加工齿轮,齿向采用高阶非对称鼓形修形.
2) 当轴线角误差γ1为0.05′时采用最大修形长度不对称的设计承载传动误差最大波动量减少了42.85%,当轴线角误差γ2为0.05′时采用最大修形量不对称的设计承载传动误差最大波动量减少了53.47%.存在轴线角误差时采用合理的齿向不对称修形参数能有效减少承载传动误差波动量,提高齿轮副的啮合性能.
3) 下一步将研究修形参数的优化设计问题,使存在轴线角误差的斜齿轮获得最佳的啮合性能.
参考文献:
[1]王统,贾毅,邱良恒,等.渐开线齿轮修形方法的进展[J].上海交通大学学报,1998,32(5):133.
WANG Tong,JIA Yi,QIU Liangheng,et al.Progress Outline of Gear Tooth Profile Modification[J].Journal of Shanghai Jiaotong University,1998,32(5):133.(in Chinese)
[2]方宗德.修形斜齿轮的轮齿接触分析[J].航空动力学报,1997,12(3):247.
FANG Zongde.Tooth Contact Analysis of Modified Helical Gears[J].Journal of Aerospace Power,1997,12(3):247.(in Chinese)
[3]LITVIN F L,GONZALEZ-PEREZ I,FUENTES A,et al.Topology of Modified Surfaces of Involute Helical Gears with Line Contact Developed for Improvement of Bearing Contact,Reduction of Transmission Errors,and Stress Analysis[J].Mathematical and Computer Modeling,2005,42(9):1063.
[4]方宗德.修形斜齿轮的承载接触分析[J].航空动力学报,1997,12(3):251.
FANG Zongde.Loaded Tooth Contact Analysis of Modified Helical Gears[J].Journal of Aerospace Power,1997,12(3):251.(in Chinese)
[5]盛钢,沈云波.基于抛物线修形的斜齿轮传动啮合特性研究[J].西安工业大学学报,2007,27(6):531.
SHENG Gang,SHEN Yunbo.The Meshing of Modified Helical Gear Drive in Profile Direction[J].Journal of Xi’an Technological University,2007,27(6):531.(in Chinese)
[6]蒋进科,方宗德,苏进展.宽斜齿轮多目标修形优化设计[J].西安交通大学学报,2014,48(8):91.
JIANG Jinke,FANG Zongde,SU Jinzhan.Multi-Objective Optinal and Modified Design for Wide Helical Gear[J].Journal of Xi’an Jiaotong University,2014,48(8):91.(in Chinese)
[7]蒋进科,方宗德,王峰.降低斜齿轮噪声的对角修形优化设计[J].振动与冲击,2014,33(7):63.
JIANG Jinke,FANG Zongde,WANG Feng.Optimal Design with Diagonal of Modification for Reducing Helical Gear Noise[J].Journal of Vibration and Shock,2014,33(7):63.(in Chinese)
[8]FAYDOR L.LITVIN,ALFONSO FUENTES.Gear Geometry and Applied Theory[M].Cambridge:Cambridge University Press,2004.
[9]方宗德,刘更,沈允文.圆柱齿轮传动的三维接触分析[J].西北工业大学学报,1992,10(1):74.
FANG Zongde,LIU Geng,SHEN Yunwen.3-D Tooth Contact Analysis of Helical Gears[J].Journal of Northwestern Polytechnical University,1992,10(1):74.
(in Chinese)
