单元网格构型的优选及基于功能梯度的轻量化研究

龚珍珍，纪小刚,2，陈 赛，闫 晨，于益超

（1.江南大学 机械工程学院，无锡 214122；2.江苏省食品先进制造装备技术重点实验室，无锡 214122）

0 引言

随着制造业的创新发展，汽车、航空航天等领域对于轻量化设计的急迫需求[1,2]，使得3D打印技术在轻量化方向的研究应用顺时而生[3,4]。现有的轻量化设计主要有两种途径：改变结构材料和进行结构优化，前者主要是在材料方面使用密度低强度高的轻量化材料替代原有材料，如铝合金、镁合金和复合材料等替代原有的钢铁、不锈钢等材料[5～7]；后者主要是运用拓扑优化等方法来实现结构的轻量化[8～10]。但是在实际应用中，涉及到功能性要求，不能改变结构的外观形状，只能从内部填充方面考虑[11]，本研究便是根据此种诉求特点产生的。

本文提出5种单元网格及其构型，这些结构不仅抗弯性能较好，且抗弯能力近似呈梯度变化。因此，根据应力分析结果，将基于功能梯度变化的单元网格填充到需要优化的实心结构中，不仅能够满足结构的强度与刚度要求，同时满足不改变零件外观的要求，从而实现轻量化。

1 材料参数性能测定

单元网格构型的力学性能分析主要是从有限元模拟与实验验证两个方向进行的。实验验证采用的构型由光敏树脂固化而成，所以首先需要测出光敏树脂的材料属性，为后续的研究做铺垫。

1.1 测试原理

为了获得光敏树脂的弯曲力学性能参数，本文参照GB/T 2567-2008制出标准弯曲试样如图1所示，采用三点弯曲试验，试验装置示意图如图2所示。已知光敏树脂材料的泊松比为0.4。

图1 3D打印弯曲试样图

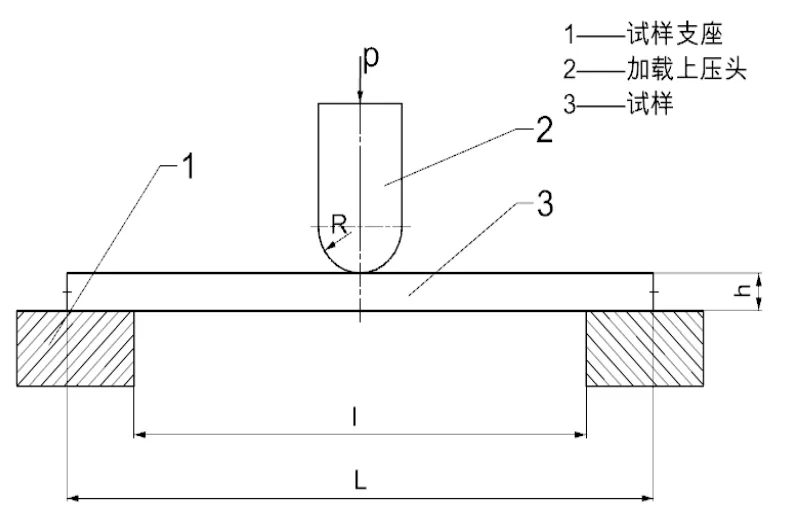
图2 三点弯曲试验装置示意图

试样厚度h为4.0±0.2mm，宽度b为15mm，长度l不小于20h，最终取如下数值：试样厚度h为4mm，宽度b为15mm，长度L为80mm，跨距l为16h=64mm，加载上压头半径R为5mm，试验速度为2mm/min。

1.2 计算公式

弯曲强度按照式(1)计算：

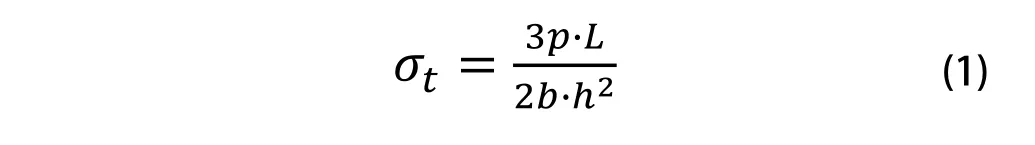
式(1)中：

P为破坏载荷(或最大载荷)，单位为牛顿（N）；

L为跨距，单位为毫米（mm）；

b为试样宽度，单位为毫米（mm）；

h为试样厚度，单位为毫米（mm）。

弯曲弹性模量按照式(2)计算：

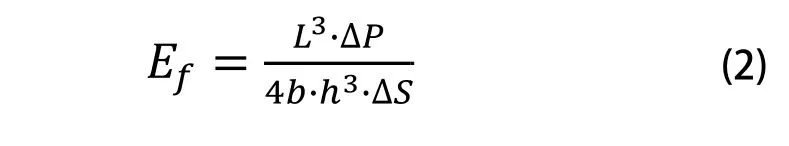
式(2)中：

Ef为弯曲弹性模量，单位为兆帕（MPa）；

∆P为对应于载荷-挠度曲线上初始直线段载荷增量值，单位为牛顿（N）；

∆S为与载荷增量对应的跨中挠度，单位为毫米（mm），其余同上式。

1.3 材料性能测试结果

进行三点弯曲试验，使用的实验器材是CTM2500万能材料试验机(最大荷重：10kN；荷重精度：±0.01%；精度等级：0.5级；位移分辨率：0.03μm)，测定时以2mm/min的速度进行加载，试验装置如图3 所示。

图3 三点弯曲试验装置图

按照GB/T 2567-2008在同等实验条件下进行了五组弯曲平行试验，最终得到光敏树脂材料的弯曲性能测试图（如图4所示）与测试结果（如表1所示）。

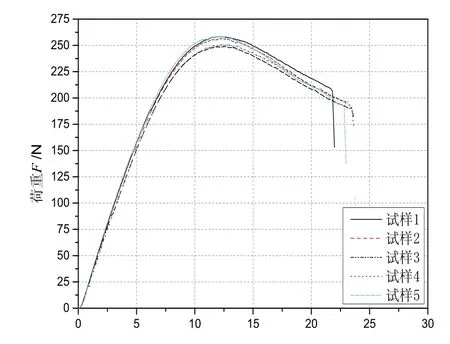
图4 标准弯曲试样测试图

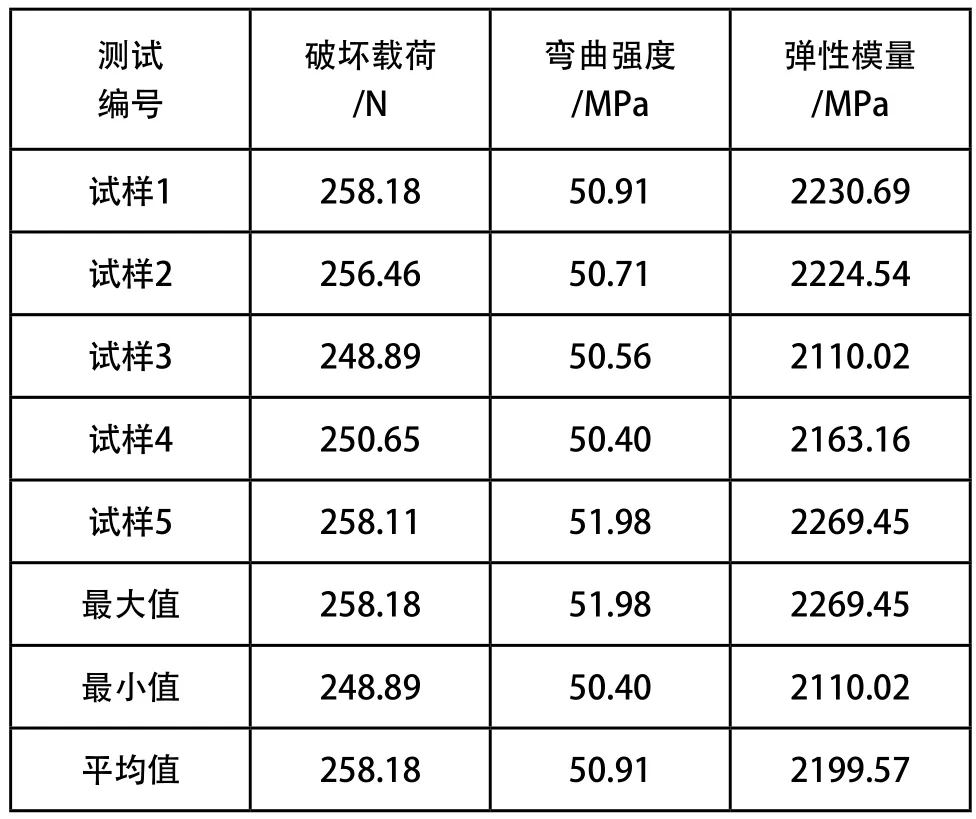
表1 光敏树脂材料弯曲性能测试结果

由以上实验测试结果可以得出，该光敏树脂的弯曲强度为σb=50.91MPa，弯曲弹性模量为E=2199MPa。出于安全性考虑，将材料的弯曲极限强度近似看作是屈服强度（后续的有限元模拟与实验分析都是将弯曲极限强度近似看作屈服强度），那么材料的屈服强度σs=50.91 MPa。

2 单元网格的设计与优选

为了从结构上进行优化实现轻量化的目的，本文设计如图5所示的5种各向同性的单元网格，用以内部 填充。

设计的单元网格是一种高孔隙率的结构，此处引入相对密度(单元网格的相对密度是指网格相对实心结构的体积比)，可以更为精确得确定填充结构的质量减轻比例，为轻量化设计提供定量数据。5种单元网格的相对密度如图6所示，构型1-5的相对密度是呈上升趋势的。

为了测试每种单元网格的抗弯能力，将每种单元网格通过阵列与刚性固接的方式组合，形成单元网格构型的“芯”。考虑到弯曲试验对象两侧需留余量以保证弯曲试验能够顺利进行，构型左右两侧各设计5mm厚的夹板，组成完整的单元网格构型，如图5所示。

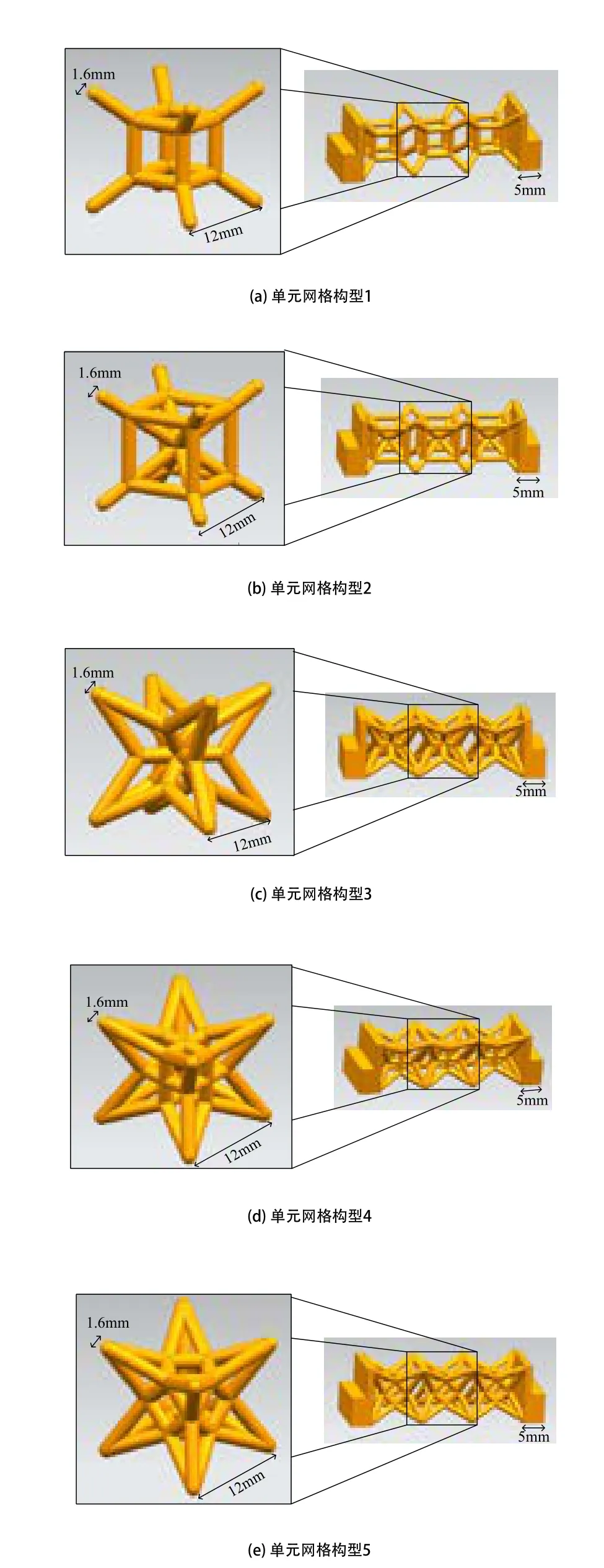
图5 五种单元网格及构型结构

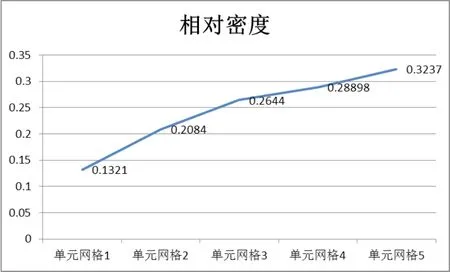
图6 单元网格的相对密度

3 有限元模拟实验

3.1 有限元模拟分析

为了验证各种单元网格构型的抗弯能力，采用商用有限元分析软件ANSYS-WORKBENCH进行分析，设置材料参数泊松比为0.4，根据材料测试结果，弹性模量设置为2199MPa。

3.1.1 有限元网格化分

利用ANSYS-WORKBENCH软件对单元网格构型进行四面体网格划分，设置网格精度为0.5mm。

3.1.2 边界条件

为了模拟实验情况，对网格构型一侧底面施加固定约束，约束x、y、z三个方向的位移为0mm，另一侧底面约束y、z方向位移为0mm，x方向自由。

3.1.3 加载条件

模拟四点弯曲试验，对单元网格构型中间4个接触点施加垂直向下的载荷。实际实验时，上压头以2mm/min的速度下压，接触到工件的瞬时是点接触，随着压头继续向下移动，点接触慢慢转化为面接触，所以在进行有限元模拟分析时，在构型的四个接触点上选取直径为0.5mm球曲面，对四个球曲面施加垂直向下即沿z轴负方向的载荷（如图7所示）。不断尝试增大载荷，直至最大等效应力达到材料的弯曲极限强度时，将此时施加的载荷看作此种构型可承受的最大破坏载荷。

3.1.4 模拟分析结果

在垂直向下的载荷逐渐增大的过程中，发现构型1-构型5分别在34.5N、69N、79N、96N、108N时，刚好近似达到弯曲极限强度值。构型1～构型5的等效应力云图以及变形云图如图8～图12所示。

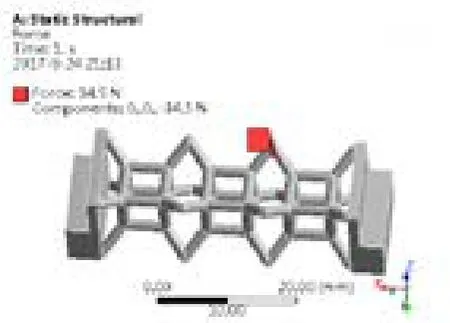
图7 单元网格构型施载图

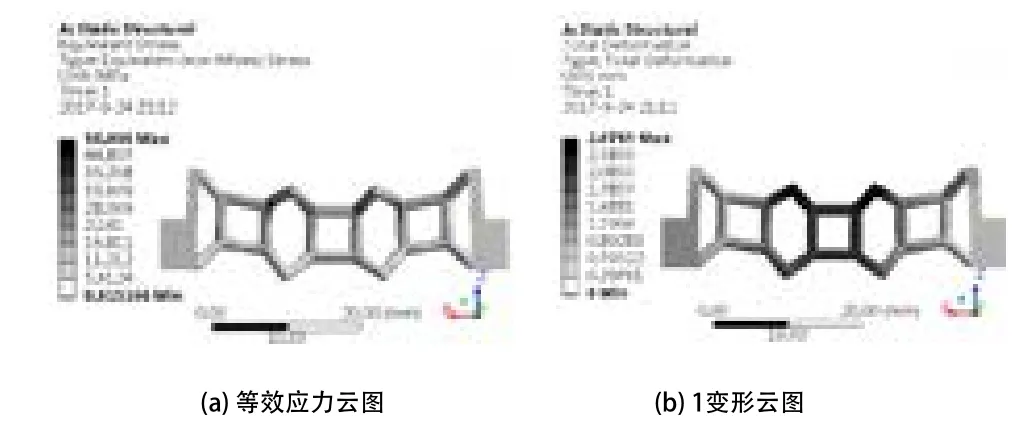
图8 构型1有限元分析结果

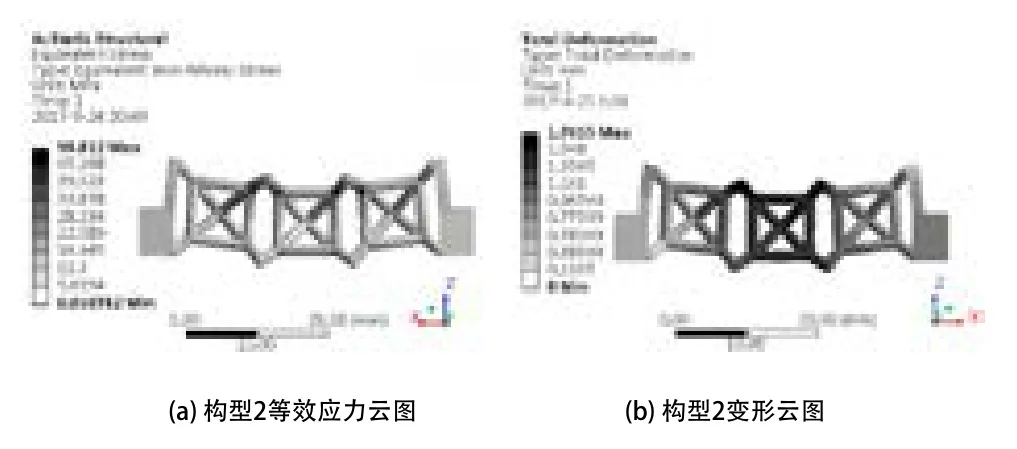
图9 构型2有限元分析结果

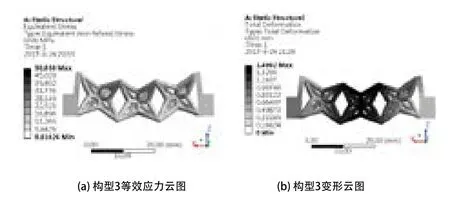
图10 构型3有限元分析结果

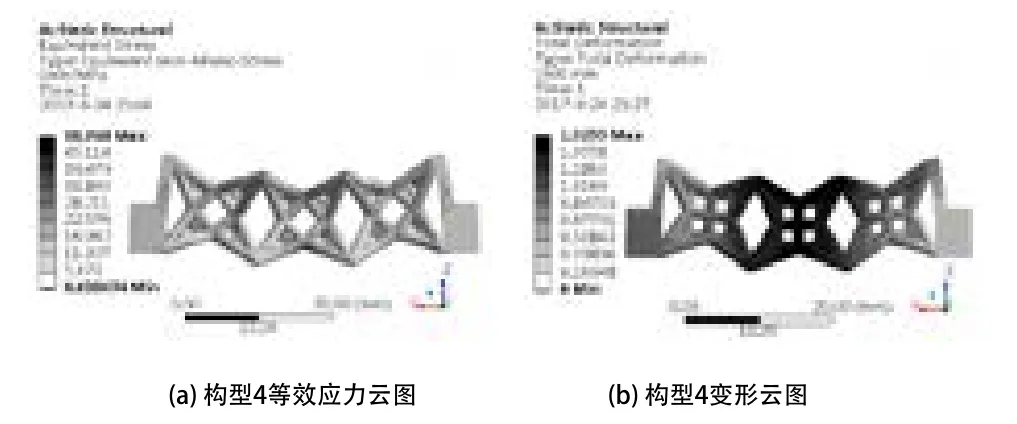
图11 构型4有限元分析结果

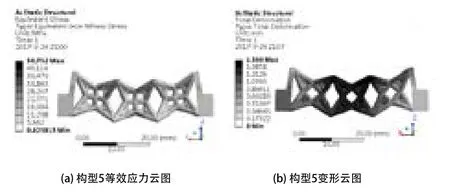
图12 构型5有限元分析结果

在近似达到弯曲极限强度值时，通过对比5种构型承受的最大破坏载荷可以看出，随着5种单元网格相对密度的增大，5种网格构型的抗弯能力呈上升趋势。

3.2 实验分析结果

设计四点弯曲实验装置如图13所示。制作模型分别进行同样的弯曲测试，试验仪器为CTM2500万能材料试验机，加载速率为2mm/min。每个试验工件总体尺寸为46mm×12mm×12mm；截面尺寸为12mm×12mm，跨距L=36mm，l=12mm，b=12mm，h=12mm，a=12mm。

图13 四点弯曲实验装置示意图与实物图

每种网格构型有3个平行试样，分别将构型1-5放置在万能材料试验机上进行弯曲测试，得到5种构型的荷重位移曲线如图14所示，每组实验的测试结果如表2所示。

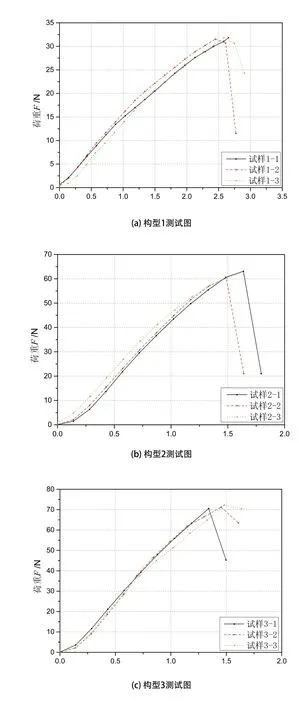
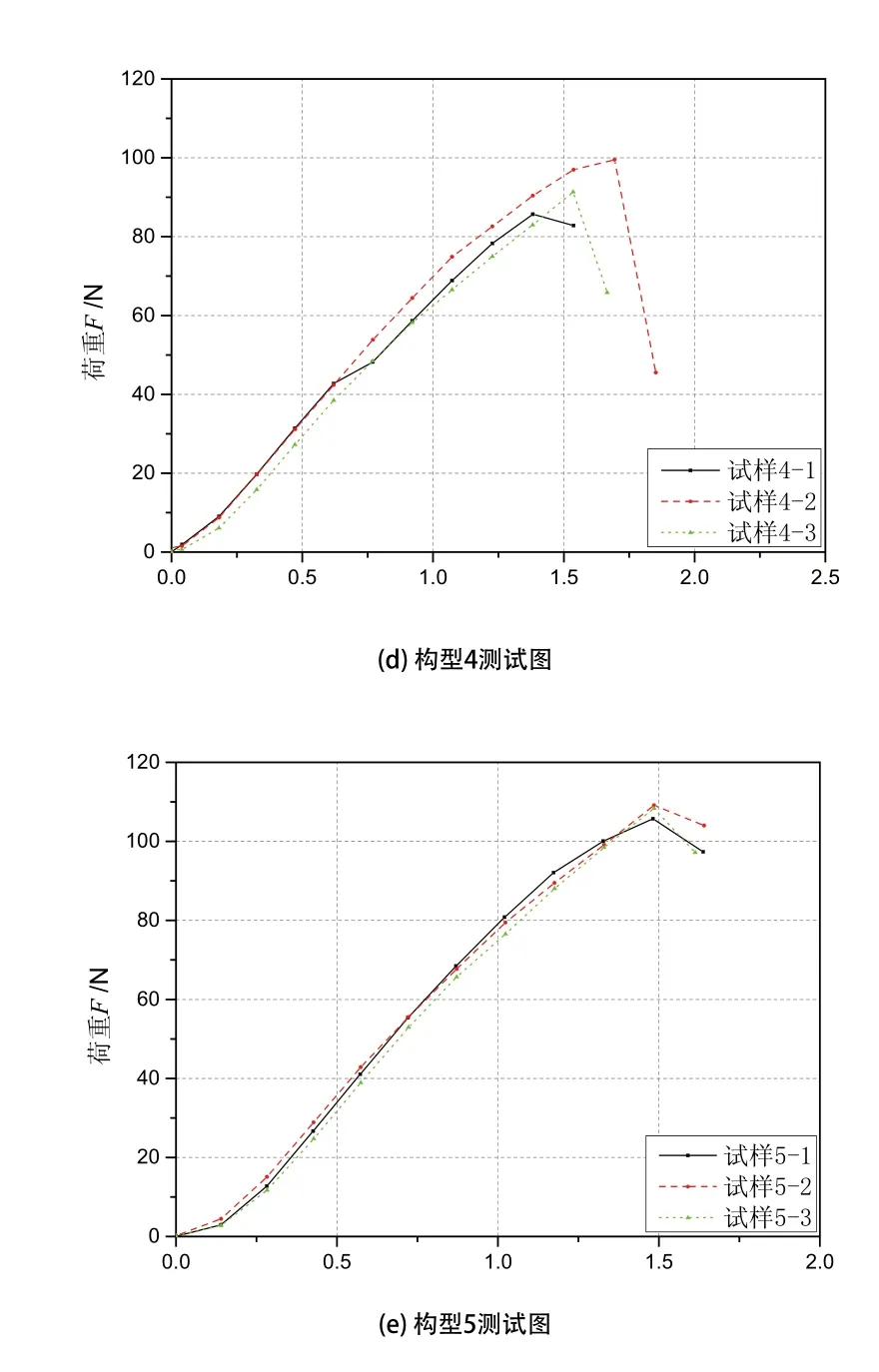
图14 5种构型的荷重位移曲线

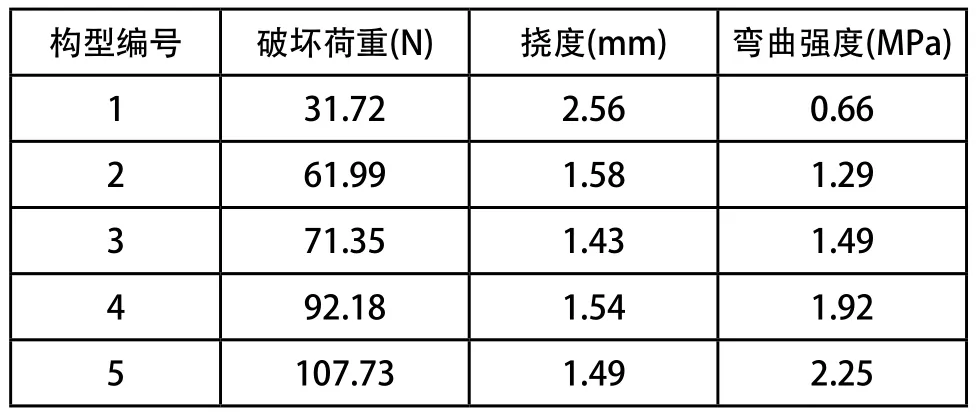
表2 5种构型的弯曲测试结果

3.3 结果对比

将构型的破坏荷重近似精确到1N，屈服点位移近似精确到0.01mm，然后对比分析模拟结果和实验结果，如表3和图15所示。

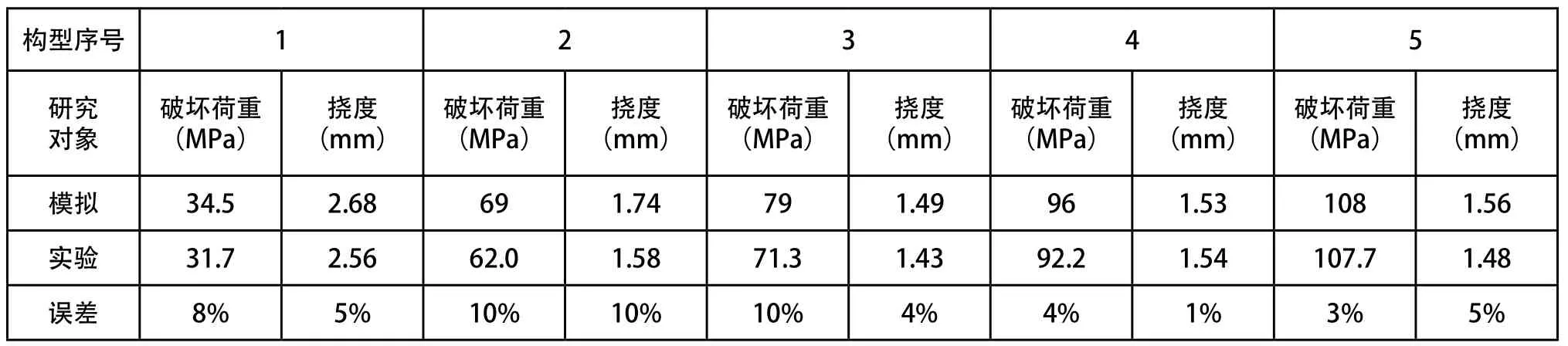
表3 实验与模拟结果对比

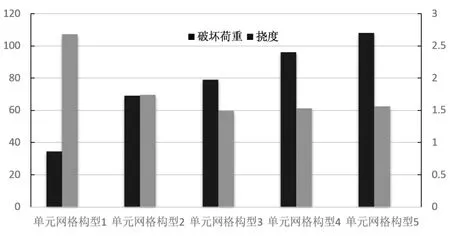
图15 实验与模拟结果对比

根据表3和图11可以看出，有限元模拟与实验误差均在10%范围内，对于数值模拟方法，该误差在可以接受范围内。5种构型能承受的破坏荷重是逐渐增大的，相应的抗弯性能越好，则挠度越小。由于单元网格4、5能承受的破坏荷重相近，而单元网格5的相对密度却大于构型4，出于减轻质量的目的，舍去单元网格5。在剩下的4种单元网格中，在满足弯曲强度的前提下，将应力区间与4种网格最大承载力的比例划分区间依次匹配，得到二者关系如表4所示。

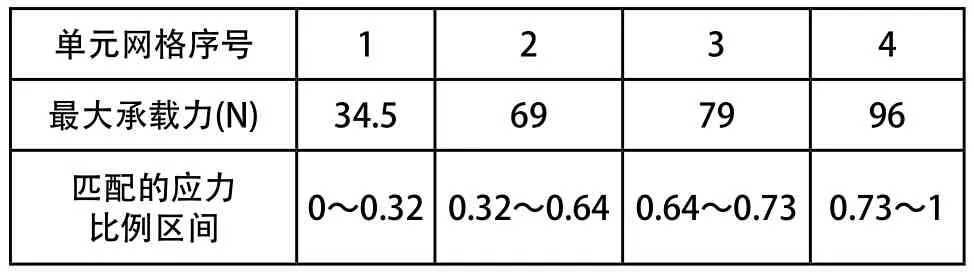
表4 单元网格与应力的匹配关系

4 实例工况分析

以空客某零件为实例研究对象，进行轻量化设计。实例是总体尺寸为53×63×88 mm的某零件，划分网格精度为0.5mm，端面受固定约束，内孔面受垂直向下1000N的力，得到有限元分析结果如图16所示。

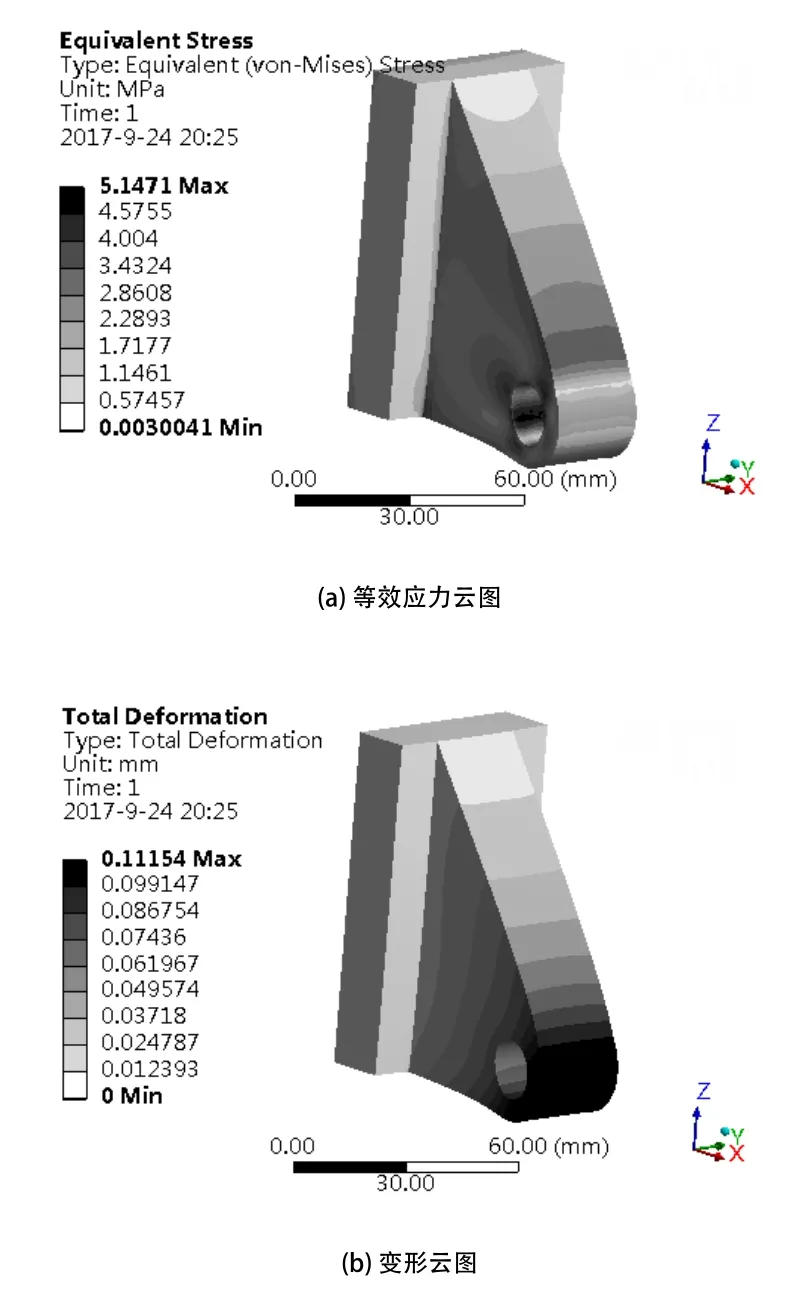
图16 空客某零件有限元分析结果

从结果可以看出，应力主要集中在内孔面周围，远离受载处应力较小，考虑将零件中间部位用单元网格根据应力区间进行填充。将4种网格以一定的方式排布连接，在A、B、C、D、E、F、G、H点（如图17）沿着高度方向进行排布，填充到实例内部。其中点坐标为A(8，18，0)、B（8，6，0）、C（8，-6，0）、D（8，-18，0）、E（20，6，0）、F（20，-6，0）、G（32，6，0）、H（32，-6，0）。

图17 空客某零件图

根据结构以及加载对称性可知，A、B、E、G四点所在的直线上应力分布情况与D、C、F、H四点所在直线上的应力分布情况一致。根据有限元分析结果A、B、E、G四点上的应力值，按照应力区间匹配关系，在通过A点的直线上，按照从下往上全部为1的网格顺序填充；在通过B点的直线上，按照2-1-1-1-1-1-1顺序填充；在通过E点的直线上，按照3-2-1-1-1顺序填充；在通过G点的直线上，按照4-3-2-1顺序填充。最终设计的单元网格填充后的零件如图18所示。

将单元网格填充后的零件施加与原实心零件同样的约束和载荷条件，得到等效应力云图和变形云图如图19所示。

图18 单元网格填充后的空客某零件结构图

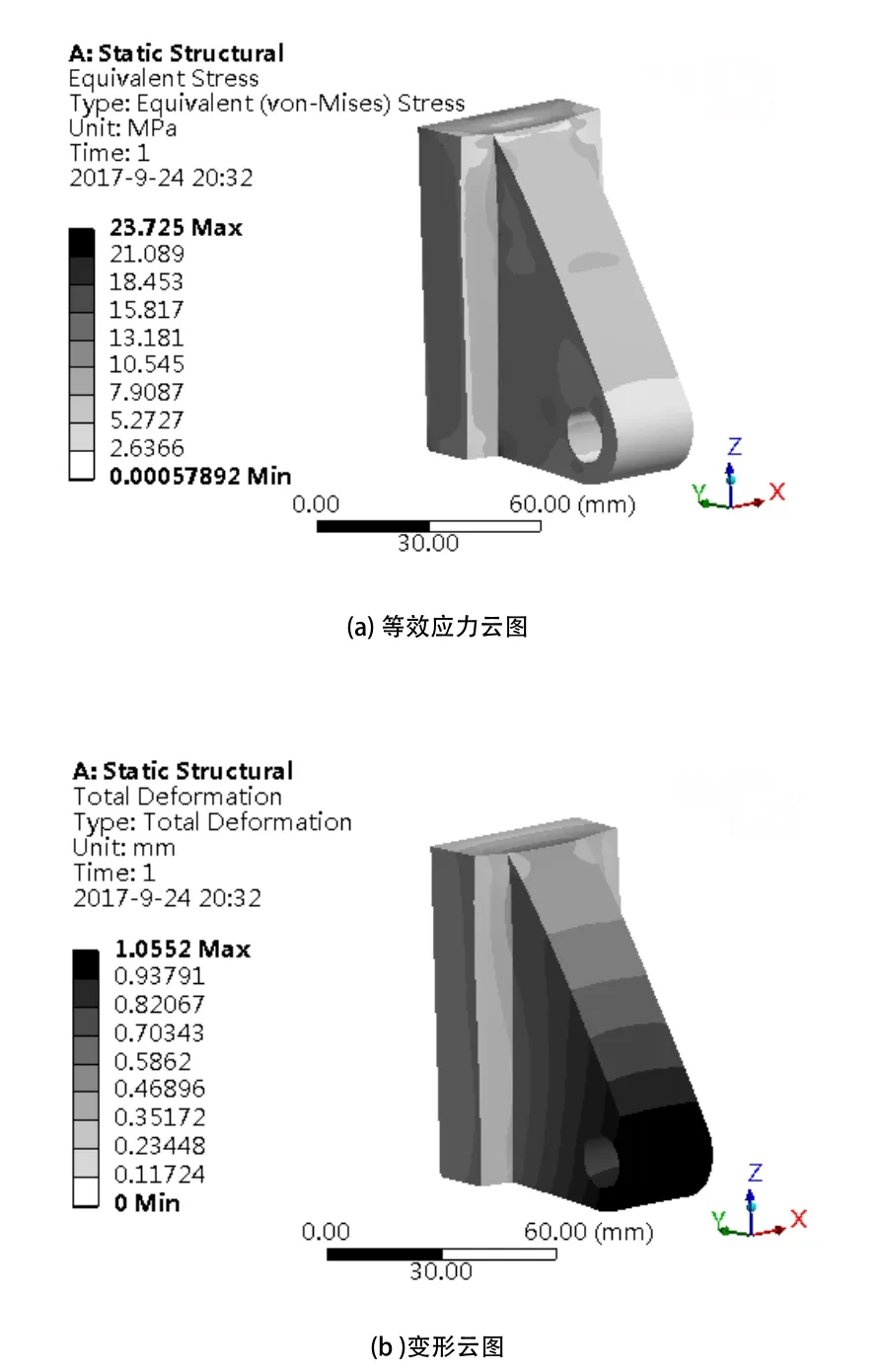
图19 单元网格填充后的空客某零件有限元分析结果

单元网格填充后的空客某零件满足了弯曲强度50.91MPa。虽然在等效应力上比原实心零件大，但仍然在其屈服强度范围内。填充后的零件相比原实心零件在质量上减轻了50.2%，实现了轻量化的目标。

5 结论

本文设计了5种各向同性的单元网格构型，通过有限元模拟和弯曲实验对比分析，筛选出了4种抗弯性能较好且依次增强的单元网格。根据网格的应力分布情况，基于功能梯度变化模式进行填充网格。经过实例验证表明，该方法可有效的减轻质量实现轻量化，具有较好的实用性与可行性。

在后续的研究中，将继续完善扩充单元网格库，为轻量化的单元网格填充方法提供更加可靠的依据，同时为深入进行轻量化设计提供了思路与参考。

参考文献：

[1]欧飞,任禾.汽车轻量化[J].中国经济和信息化,2013,10:84-86.

[2]Moon S K, Yu E T, Hwang J, et al. Application of 3D printing technology for designing light-weight unmanned aerial vehicle wing structures[J]. International Journal of Precision Engineering and Manufacturing-Green Technology,2014,1(3):223-228.

[3]Bose S, Vahabzadeh S, Bandyopadhyay A.Bone tissue engineering using 3D printing[J].Materials Today,2013,16(12): 496-504.

[4]李青,王青.3D打印:一种新兴的学习技术[J].远程教育杂志, 2013,04:29-35.

[5]Starke E A, Staley J T. 24–Application of modern aluminium alloys to aircraft[J].Fundamentals of Aluminium Metallurgy, 2011:747-783.

[6]姚志英.镁合金自行车车架技术研究[D].南京理工大学,2015.

[7]徐中明,徐小飞,万鑫铭,等.铝合金保险杠防撞梁结构优化设计[J].机械工程学报,2013,49(8):136-142.

[8]Niral P, Chauhan M. FEA and Topology Optimiz- ation of 1000T Clamp Cylinder for Injection Mo- lding Machine[J].Procedia Engineering,2013,51:617-623.

[9]Oktay E, Akay H U, Sehitoglu O T. Three-dime- nsional structural topology optimization of aerial vehiclesunder aerodynamic loads[J]. Computers & Fluids, 2014,92:225-232.

[10]James K A, Kennedy G J, Martins J. Concurrent aerostructural topology optimization of a wing box[J].Computers and Structures, 2014, 134,1-17.

[11]Moon S K, Yu E T, Hwang J, et al. Application of 3D printing technology for designing light-weig- htunmanned aerial vehicle wing structures[J].International Journal of Precision Engineering and Manufacturing-Green Technology,2014,1(3):223-228.