双曲线函数拟合工程沉降规律的方法研究

(江苏建筑职业技术学院 建筑设备与市政工程学院，江苏 徐州　221116)

1　研究背景

双曲线回归函数(以下简称双曲线函数)常用于拟合工程沉降量随时间的变化规律[1-4]。对于该函数的回归计算，数理统计教科书、以往科技文献以及生产实际中常用的方法是：首先，通过变量代换转化为线性模型，并利用线性回归方法推求线性回归系数；然后，根据线性回归系数反求双曲线函数的回归系数。这种方法称为线性化回归方法。该方法看似合理，其实不然。对于双曲线函数，本文列举了线性化回归方法出现回归失真实例，并基于双曲线函数的因变量与将该函数线性化后的因变量二者的残差平方和之间的关系式，分析了线性化回归方法可能导致回归失真的原因；提出应采用高斯-牛顿法等非线性回归方法进行双曲线函数回归计算，并给出了借助MATLAB软件进行求解的方法。

2　采用线性化回归方法的失真现象与分析

丹土一级公路03A标伍家岭隧道右线k2+546断面测点E累计沉降值随时间变化实测值见表1，通过回归计算，用于预测隧道在该测点的沉降趋势。

采用双曲线函数拟合表1数据，其回归模型为

(1)

式中：A，B为待估参数。

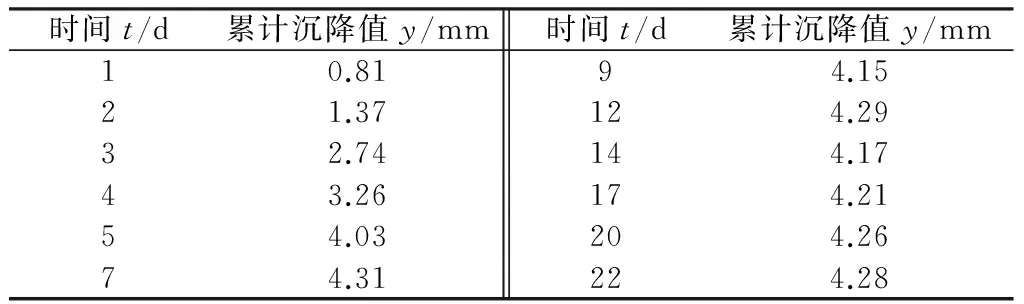
表1　伍家岭隧道测点E累计沉降值随时间变化的实测数据

2.1　线性化回归方法的失真现象

设v=1/y,x=1/t,将式(1)线性化：

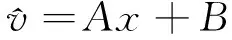
(2)

然后，将表1的样本观察值(ti,yi)转化为(vi,xi),i=1～12，对式(2)线性回归得：A=1.074 94，B=0.123 04，拟合直线见图1，线性回归的相关系数r=0.975 8，样本点n=12，查相关系数检验临界值r0.01=0.707 9，可见线性回归的相关系数r大于相关系数检验临界值r0.01=0.707 9，线性相关显著。

根据上述线性回归结果，求得非线性回归系数A=1.074 94，B=0.123 04，进而用式(3)计算曲线回归的相关指数(也称确定性系数)R2：

(3)

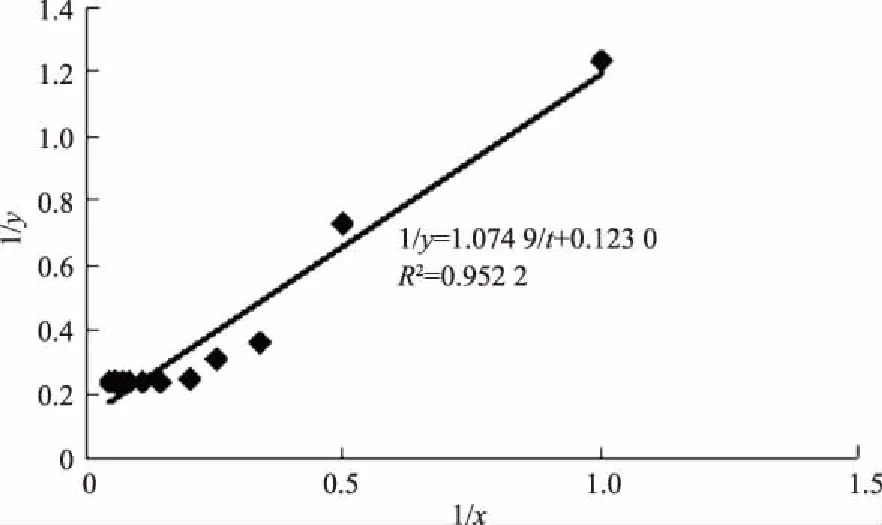
图1　实例1线性化的拟合直线

时间t/d累计沉降值yi/mmvi=1/yiy4i^vi=Ax+B(vi-^vi)2(vi-^vi)2y4i^yi=tiA+Bti(yi-^yi)210.811.23460.43051.19800.00130.00060.83470.000621.370.72993.52280.66050.00480.01701.51400.020732.740.365056.36410.48140.01350.76352.07750.438943.260.3067112.94590.39180.00720.81652.55250.500654.030.2481263.76680.33800.00812.13122.95831.148574.310.2320345.07150.27660.00200.68593.61530.482694.150.2410296.61450.24250.00000.00074.12410.0007124.290.2331338.71090.21260.00040.14214.70330.1708144.170.2398302.37380.19980.00160.48355.00450.6963174.210.2375314.14370.18630.00260.82545.36851.3421204.260.2347329.33540.17680.00341.10625.65651.9503224.280.2336335.56380.17190.00381.27935.81732.3633合计0.04888.25199.1154

结果为R2=0.448 5。绘出双曲线回归函数的拟合曲线如图2所示。

图2　实例1采用线性化回归方法所得的拟合曲线

上述计算结果表明，采用线性化回归方法，尽管变量代换后线性回归的拟合效果较好，但由其求得的双曲线回归方程拟合实测数据的效果并不好，拟合曲线未能反映实测点的分布情况。尽管对双曲线线性化后的相关系数平方r2=0.952 2,接近1，而曲线回归的相关指数R2却较小，出现了拟合失真现象。

2.2　失真现象分析

(4)

(5)

3　双曲线函数的非线性回归方法及实现

为提高双曲线函数的拟合精度，本文提出应采用高斯-牛顿法、麦夸尔特法等非线性回归方法。

一般地，对于一元非线性模型

y=f(x,θ)+ε

式中，f为一般函数；θ为P维参数向量，即θ=(θ1,θ2,…,θp)′；ε为随机误差项，且ε服从N(0，σ2)。设y和x具有n组观察值(xi，yi)，i=1～n。高斯-牛顿法求解非线性模型参数的“最小二乘”估计的参数递推公式[6]，写成矩阵形式为

θ(k+1)=θ(k)+[J′(θ(k))J(θ(k))]-1×

J′(θ(k))[(y-f(θ(k))]

(6)

(7)

式中，k为递推次数；向量y=(y1,y2,…,yi，…,yn)′，yi为因变量第i个观察值；向量f(θ(k))=[f1(θ(k)),f2(θ(k)), …,fi(θ(k)) , …,fn(θ(k))]′，fi(θ(k))为由非线性方程及第k次迭代参数计算的因变量y的第i个估计值，i=1～n。

实例1拟合双曲线函数，采用高斯-牛顿法回归计算的步骤如下。

(1)分别对式(1)中参数A、B求偏导数：

(9)

(10)

(2)可利用实测值中任两组关系值求待估参数A，B的初值θ(0)。例如采用(4，3.26)、(14，4.17)，得θ(0)=(0.39，0.21)。

(3)利用θ(0)、式(8)～(9)及n组实测值(ti，yi)，i=1～n，计算偏导数矩阵J(θ(0))及f(θ(0))，进而根据式(6)进行迭代计算，直到θ(k)收敛稳定，即|θ(k+1)-θ(k)|小于或等于预先指定的小正数(例如δ=0.000 5)，从而得到非线性回归系数A，B的估计值。

对实例1采用高斯-牛顿法参数的递推结果见表3，误差平方和2.156 6远小于线性化方法的误差平方和 9.115 4。进一步计算相关指数R2=0.869 5, 远大于采用线性化方法所得双曲线回归方程求得的相关指数的R2=0.448 5，拟合曲线如图3中实线所示。可见，拟合效果显著优于线性化回归方法。

表3　实例1高斯-牛顿法参数的递推结果

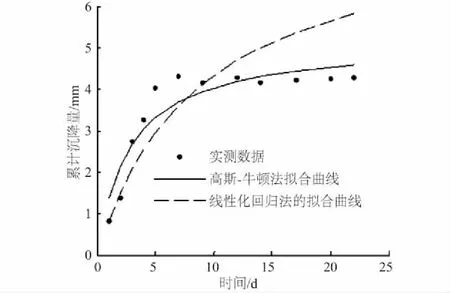
图3　实例1由不同方法所得拟合曲线比较

上述计算也可调用MATLAB软件中nlinfit函数进行非线性回归计算，具体方法如下[7-8]。

function yhat=volumsq(beta,t)

yhat=t./(beta(1)+ beta(2)t)

(2)在命令窗口输入

t=[1,2,3,4,5,7,9,12,14,17,20,22]

y=[0.81,1.37,2.74,3.26,4.03,4.31,4.15,4.29,4.17,4.21,4.26,4.28]

beta0=[0.39,0.21]′

[beta]= nlinfit(t′,y′,′volumsq′,beta0);

beta

得结果beta=[0.537 2,0.193 9]′。

实例2 文献[3]中温岭东海塘软基公路工程，由观测的时间t与实测累计沉降量y的关系值点绘关系点见图4[3]，其规律可用双曲线函数式(1)进行拟合。采用线性化回归方法、高斯-牛顿法的计算结果见表4；1/y与1/t线性回归直线如图5所示，线性化方法和高斯-牛顿法所得双曲线分别如图4虚线和实线所示。由计算结果可见，尽管线性相关系数的平方r2=0.988 8(r=0.994 4，线性相关高度显著)，但由线性化方法所得双曲线拟合效果并不理想，而采用高斯-牛顿法进行非线性回归显著优于线性化回归方法。

表4　实例2不同回归方法求得双曲线回归的计算结果

图4　实例2不同方法所得的拟合曲线比较

图5　实例2线性化的拟合直线

4　结　语

从理论上分析了双曲线函数因变量与其线性化后的因变量的残差平方和之间的关系式，该式表明，线性化回归方法无法满足双曲线函数的因变量的残差平方和为最小，并且结合双曲线函数采用线性化回归方法出现回归失真的实例，分析了线性化回归方法导致其回归失真的原因。

双曲线函数回归计算的实例表明，采用高斯-牛顿法进行非线性回归计算，其拟合效果显著优于线性化回归方法。因此，应采用高斯-牛顿法等非线性回归方法进行双曲线函数的回归计算。本文给出了借助MATLAB软件中的nlinfit函数进行非线性回归计算的方法，易于实现。

参考文献:

[1]倪锦初,李晓伟,张治军，等.高填方渠道施工期沉降预测分析[J]. 人民长江,2014,45(6):85-88.

[2]王元柱,梁城.隧道监控量测数据的回归分析[J].土工基础,2013,27(5):70-72.

[3]金锡斐,江维文.双曲线法在软土地基沉降预测中的适用性研究[J].浙江水利科技,2008(5): 47-48.

[4]李彦杰，黄斌，谭凡，等.堆载预压法在在深圳机场软基处理中的应用[J]，人民长江，2010，41(S):21-23.

[5]张子贤.可线性化的非线性回归的有关问题与几种回归方法的比较[J].数学的实践与认识, 2015,45(18): 167-173.

[6]袁志发,周静芋.多元统计分析[M].北京:科学出版社,2002.

[7]周品.MATLAB概率与数理统计[M].北京:清华大学出版社, 2012.

[8]谢中华,李国栋,刘焕进,等.MATLAB从零到进阶[M].北京:北京航空航天大学出版社, 2012.