基于复杂网络的电网结构静态鲁棒性分析
2018-04-09吴正平曹诗龙
汪 昊,吴正平,程 洁,曹诗龙
(1.三峡大学 电气与新能源学院,湖北 宜昌 443002;2.武汉供电公司检修公司变电运维室,湖北 武汉 430000;3.国网湖北省电力公司检修公司,湖北 武汉 430050)
0 引 言
20世纪末期,自从美国康奈尔大学的Watts和Strogatz在《Nature》杂志上发表了题为《Collective Dynamics of ‘Small-World’ Networks》(“小世界”网络的群集动力学)的文章[1],小世界网络模型第一次展现到人们面前。而后在1999年美国圣母大学的Barabàsi和Albert在《Science》发表了题为《Emergence of Scaling in Random Networks》(随机网络中标度的涌现)的文章[2]。文献[1]和[2]的发表在全球掀起了一股研究复杂网络的热潮。2013年,Pagani和Aiello在《Physica A》上发表了题为《The power grid as a complex network: Asurvey》(电力网络作为一个复杂网络:调查)的文章[3],阐述了在电网中可以将发电机、传输线抽象为网络中的节点和边来建模,即可以用复杂网络的理论来研究电力网络。至此,电力系统领域的科研工作者开始用复杂网络的观点来分析电力系统。本文在经典的节点导纳矩阵模型基础上,将节点分类,简化计算,并从复杂网络的角度提出三种不同的攻击策略,利用静态分析的方法,从电网结构的角度阐述其结构对鲁棒性的影响,最后用IEEE-57系统和IEEE-118系统作为算例加以验证。
1 电力网络建模
根据网络的特性,电力网络可以被看作是一个典型的复杂网络,电网中的节点和支路可以被视为是复杂网络中的点和边。对于一个有n个节点的网络,其经典的网络参数模型是由Grainger和Stevenson提出的节点导纳模型,即:
(1)
式中,vi和Ii分别为在节点处的节点电压和外部注入电流;Yii为节点i的自导纳;Yij为节点i和节点j的互导纳。
在上述的节点导纳矩阵模型中,利用电网的特殊性根据不同的节点性质,将节点分为以下三类:
(1)负荷节点
负荷节点i消耗电能,并在节点处注入电流Ii,因此在负荷节点处的电流值为负数。即:
*V=Ii
(2)
式中,V=[…vivjvk…]T。
(2)分布节点
分布节点又称为联络节点,分布节点j是一个连接节点,它既不产生也不消耗电能,因此令Ij=0,即:
*V=0
(3)
(3)发电机节点
发电机节点k可以看做一个混合的电压源,从这个节点流出的电流取决于其电压值与网络拓扑结构及电气信息,即:
*V=vk
(4)
式中,yk=1,vk是节点k的电压。
2 复杂网络的统计描述及电网结构鲁棒性指标
2.1 复杂网络的统计描述
复杂网络的特征通常隐藏在其统计性质中,人们对其统计性质也提出了许多概念[4]。由于其概念较多,仅介绍三种本文所用的基本概念。
(1) 最短路径长度
在网络中,最短路径长度li,j定义为任意两点i和j之间的最短路径上的边数。
(2)度
在网络中,节点i的度ki定义为与该节点连接的边数。所以直观上来看,如果一个节点的度越大,那么这个节点在某种意义上就越“重要”。
(3)介数
在网络中,有的节点的度不大,但是这个节点可能起到网络中两个部分的连接桥梁作用,说明这个节点也是很重要的,因此定义在网络的所有节点中,经过节点i的所有最短路径的数量Bi为节点i的介数。
2.2 电网结构鲁棒性指标
鲁棒性是指当系统发生了结构或者大小等变化后,系统能够维持其原有性能的能力[5]。而对于电网的结构鲁棒性可以认为是当电网的结构发生变化之后,电网系统能够维持其原有供电功能的能力。
因此根据电网结构的特殊性,定义了如下2个电网结构鲁棒性的指标。
(1)电网节点移除比
定义电网节点移除比为,在电网中,电网结构因为故障移除的节点数与电网所有节点数之比:
(5)
式中,N为电网总节点数;nb为电网结构因故障移除数。
(2) 电网结构最大连通度
一个电网在发生故障后由于某些元件的退出,可能会使一个连通的网络分裂为若干个自身连通的“孤网”,那么定义电网结构最大连通度为故障后最大连通子集内的节点数与电网总节点数之比:
(6)
式中,N为全网所有节点;nr为故障后最大连通子集内的节点数。
3 基于静态分析法的电网结构鲁棒性分析
在实际电网中,因为故障等原因,或多或少地将改变原有电网的拓扑结构。其中包括故障初始点以及由于故障初始点引起的连锁故障节点的退出。本文主要研究因为元件的移除数量以及策略对电网结构鲁棒性的影响,即静态分析,不考虑电网节点或边移除后的潮流分布导致的连锁故障反应。
3.1 故障模拟方法
在复杂网络中,网络的元件移除法按其移除方式可分为蓄意移除和随机移除。而在本文所研究的电力网络中,模拟故障的蓄意攻击和随机攻击的攻击对象为节点或边。针对电网结构的特殊性,制定了以下三种攻击方式:
(1)节点度数的攻击策略:首先移除网络中度数最大节点,然后计算生成新的网络中的各节点度数,再移除该节点,如此重复直至满足所设定的电网节点移除比。
(2)节点介数的攻击策略:首先移除网络中介数最大节点,然后计算生成新的网络中的各节点介数,再移除该节点,如此重复直至满足所设定的电网节点移除比。
(3)节点随机攻击策略:随机移除数量为我们所设置的电网节点移除比的数量的节点,由于随机攻击的偶然性,重复20次试验取其平均值。
3.2 故障模拟流程
基于静态分析法的电网结构鲁棒性分析是只考虑电网拓扑结构对其自身鲁棒性的影响,不考虑其电网内元件因为移除而产生的潮流重新分配及其连锁反应。所以我们研究的是在设定不同的电网节点移除比的情况下,不同的攻击模式对电网结构鲁棒性的影响。
具体流程如下:
(1)初始化:根据初始数据生成网络拓扑,并计算出该网络的各节点的介数和度等参数,同时确定本次试验的电网节点移除比。
(2)根据选定的攻击模式进行节点移除,直至满足所设定的值。
(3)生成最终的网络拓扑模型,计算出该模型的电网结构最大连通度并记录数据。
(4)重复多次,记录在不同设定值和不同攻击模式下的最终拓扑的最大连通度,并绘制其与电网移除比设定的曲线图。
其流程图如图1所示。
4 算例验证
根据上文所描述的算法,本文选用IEEE-118节点系统和IEEE-57节点系统加以仿真验证。
4.1 IEEE-118节点系统
根据前文所设定的攻击方法,分别进行以最大度数、最大介数、随机的方式进行攻击,其电网结构最大连通度(S)与电网节点移除比(PN)的关系如表1、图2所示。
根据上述仿真结果,可以看到在不同的攻击模式下,系统的连通性呈现出不同的结果,其中以随机攻击对系统影响最小,而介数攻击呈现的最为严重,这也和介数的定义相符合。而度数攻击在15%设定值后,连通度猛降说明当系统节点缺失到一定程度时,会发生量变到质变的转换。

图1 流程图

表1 IEEE-118节点系统S在不同设定PN值与不同攻击模式下的结果
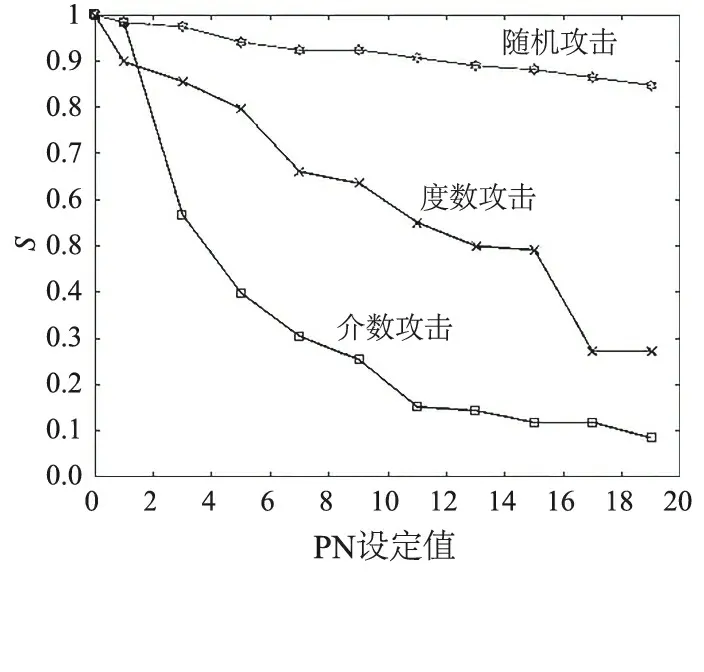
图2 IEEE⁃118节点系统S在不同设定PN值与不同攻击模式下的结果
4.2 IEEE-57节点系统
根据前文所设定的攻击方法,分别进行以最大度数、最大介数、随机的方式进行攻击,其电网结构最大连通度(S)与电网节点移除比(PN)的关系如表2、图3所示。
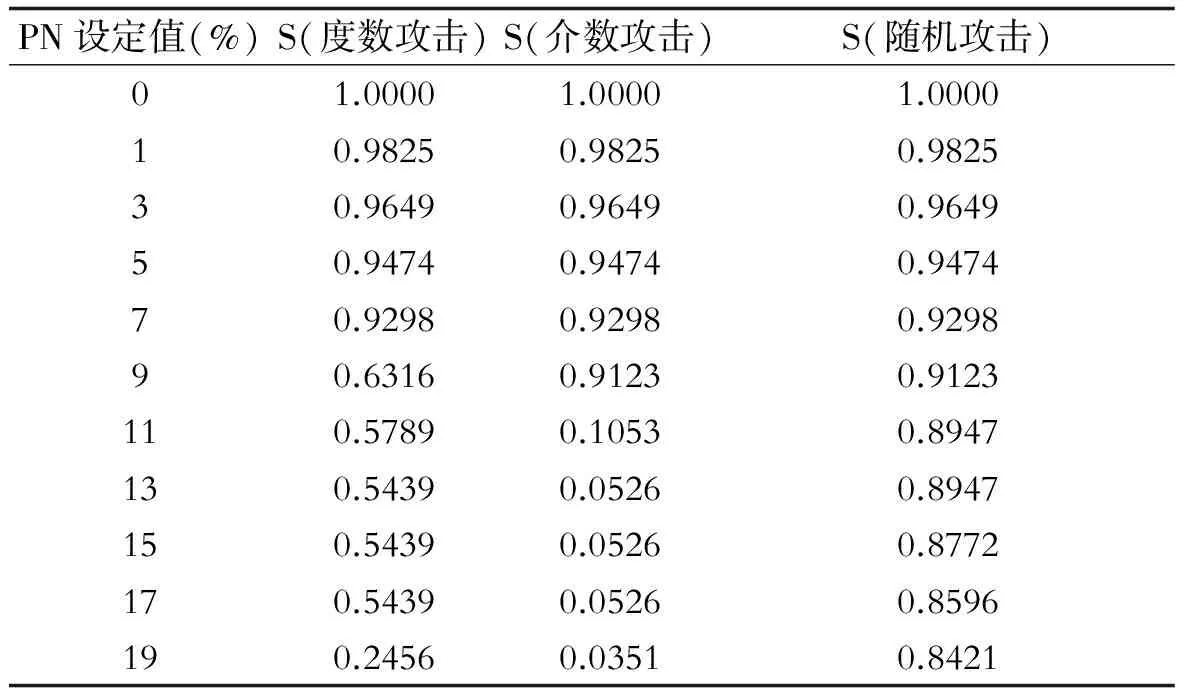
表2 IEEE-57节点系统S在不同设定PN值与不同攻击模式下的结果

图3 IEEE⁃57节点系统S在不同设定PN值与不同攻击模式下的结果
可以看到和IEEE-118节点系统的仿真结果相似,在不同攻击模式下,随机攻击影响最小,介数攻击影响最大。而在系统瓦解方面,IEEE-57节点相比于IEEE-118节点在更小的PN设定值时已经开始导致系统严重瘫痪,这也说明系统的鲁棒性也与其本身的规模有关。
5 结 论
本文通过电力网络建模,对系统内节点进行分类,并利用复杂网络相关理论对其进行统计分析,求得其统计性描述指标。针对其网络制定不同的基于复杂网络理论的攻击模式对其攻击,同时也定义了与之相对的系统结构鲁棒性的描述性指标。最后通过对IEEE-118和IEEE-57节点系统在不同设定值下按照不同模式进行攻击,得出系统中介数大的点更重要的结论,同时得出系统的鲁棒性与其规模有关的结论。因为在以后的电网设计中可以考虑其复杂网络特性提高其鲁棒性。
参考文献:
[1]Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393:440-442.
[2]Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439):509.
[3]Pagani G A, Aiello M. The Power Gridas a complex network: A survey[J]. Physica A Statistical Mechanics & Its Applications, 2013, 392(11):2688-2700.
[4]孙玺菁, 司守奎. 复杂网络算法与应用[M].北京: 国防工业出版社, 2015.
[5]Watts D J. A simple model of global cascades on random networks.[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(9):5766-5771.
