二维图像强度-几何相关系数的统计研究方法
2018-04-09张彬彬
段 汕,张 晔,张彬彬
(中南民族大学 数学与统计学学院,武汉 430074)
在Pyt′ev的形态学[1]框架下,二维图像采用的是一种强度-几何模型[1,2],图像表现为空间域划分下的分片常函数形式. 空间域的划分提供了图像确定的几何形状信息,不同图像几何形状的比较则是通过各类相关系数的建立刻画形状的相似程度. 在基于投影算子的比较方法[3-6]中,图像表示是其重要的组成部分,其中图像几何形状的分布是确定的,所对应的强度向量反映不同季节、时间、气候、光照条件、光谱范围下所获取的同一场景的不同图像. 在此意义下,多种形式的相关系数被研究. Vizilter在其研究工作[3]中,将图像的强度向量视为n维随机向量,在独立同分布、零均值的条件下,研究了一类“强度-几何”相关系数,其结果是对Pyt′ev[1]的“几何”相关系数研究成果的推广.
将图像的强度向量视为随机向量,使得对相似性度量的量化方法需要有相应的调整. 一个最直接的选择是将随机向量的统计量引入相关系数的表示中,Vizilter在文献[3]中便是选用的这种处理方法. 在实际问题中,图像强度随机向量的独立同分布是一种相对理想的假设,大多数情况下则表现为相关性的分布取值. 因此,本文在减少对强度随机向量各种限制的情况下,将文献[3]中的方法进行了推广,所建立的图像几何形状相关系数将文[3]中的诸多系数作为其特例,其研究结果更符合图像的自然构成. 此外,文中还提出并研究了一系列新的相关系数形式,使得图像几何形状的比较工具更为丰富.
1 预备知识
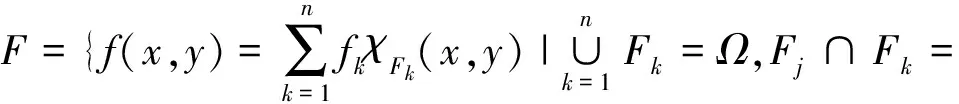
F={F1,F2,…,Fn}是对图像f(x,y)空间域Ω的划分,f=(f1,f2,…,fn)T∈Rn是f(x,y)的强度向量. 图像f作为Hilbert空间L2(Ω)中的元素,其范数‖f‖2=(f,f),图像间的Euclidean距离dE(g,f)=‖g-f‖,且F⊆L2(Ω)是L2(Ω)的凸闭子空间.
(1)
进行度量,其中PG是空间G上的投影算子:
这里fGk=(f,χGk)/‖χGk‖2,‖χGk‖2,k=1,2,…,m是划分G的子区域Gk的面积.
在分片常函数图像的“强度-几何”模型下,图像的强度和几何特征是通过强度向量和空间域的划分来描述的.在基于投影算子相关系数的研究中,划分区域的面积是重要的几何特征量,划分区域上图像强度的取值若视为一随机变量,则其分布与子区域的面积相关.为此,引入基于面积的相关变量:设A为空间域Ω的面积,sFi=(χFi,χFi)=‖χFi‖2为Fi的面积,sGj=(χGj,χGj)=‖χGj‖2为Gj的面积,sij=(χFi,χGj)为Fi∩Gj的面积.显然有:
将图像f的形状F={F1,F2,…,Fn}及图像g的形状G={G1,G2,…,Gm}视为随机场,在空间域Ω固定的条件下,应用互信息的相关方法,这些面积变量对应于形状随机场的边缘和联合概率分布为:
pF(fi)=sFi/A,pG(gj)=sGj/A,pFG(fi,gj)=sij/A,pF|G(fi|gj)=sij/sGj.
在图像的分片随机模型描述方式下,图像f的强度f=(f1,f2,…,fn)T分布建立在其形状随机场F相关分布的基础上.
2 强度-几何相关系数
考虑图像f(x,y)的强度随机向量f=(f1,f2,…,fn)T中第i个强度随机变量fi的均值E(fi)=μi,协方差cov(fi,fk)=σik(i,k=1,2,…,n)及图像f的强度均值f0=(μ1,μ2,…,μn)T. 用中心化图像f-f0=(f1-μ1,f2-μ2,…,fn-μn)T替代f,利用形状随机场的边缘和联合概率分布,可以计算出中心化图像f-f0的相关量化表示形式:
(2)
其中:
(3)
在(1)式中,引入图像f的均方范数替代范数,建立形状F与形状G的中心化强度-几何均方形态相关系数:
(4)
其中:
引入系数矩阵:
sF=diag(sF1,sF2,…,sFn);Λ=diag(σ11,σ22,…,σnn),
(5)
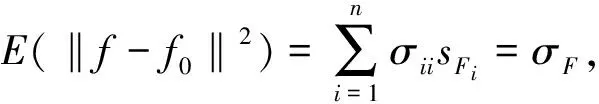
(6)
其中:
(7)
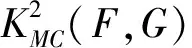
及特性函数的线性相关系数:

3 几何相关系数
(1)当随机变量fi(i=1,2,…,n)相互独立时,σik=0,i≠k,∑=Λ,此时
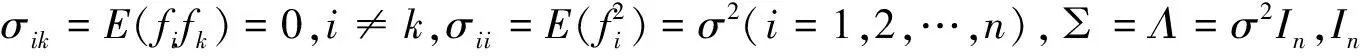
(8)
(9)

故:
此时,相关系数:
(10)
这也即是文献[1]中系数的形式. 利用(8)、(10)式还可以表示为以下形式:
4 序化几何相关系数
在Pyt′ev的图像模型下,如果强度向量f=(f1,f2,…,fn)T满足:f1 对于给定的图像f和g,设强度向量f=(f1,f2,…,fn)T和g=(g1,g2,…,gm)T中的分量均是两两互异的,则可通过以下的序化函数实现其基于强度的形状排序. 在空间域Ω上对每一个Fi(或Gj)定义其上的强度序化函数: 由函数μ+(x,y),μ-(x,y)或μ(x,y)在Ω上的取值分布,即可实现对图像强度的排序,从而获得有序形状F+={F1F2…Fn}和G+={G1G2…Gm}. 且序化函数与有序形状F+有如下关系:若i 有序形状F+={F1F2…Fn}和G+={G1G2…Gm}的比较可以通过局部序化的方法将序化因素植入相关系数: (11) 或: (12) (13) (14) 类似地,还可以得到由(12)式所导出的单边序化几何相关系数. 在特殊情况下,(11)式具有特定的结构,以上的系数将取特定的值. 如当取G+=F+时: 一般地,(13)和(14)式的取值范围是[-1,1],且关于F+,G+对称. 如果取μ+(x,y)或μ-(x,y)为序化函数,则可以避免系数取负值,此时取值范围是[0,1]. 本文对Vizilter在文献[3]中的研究工作进行了推广,通过引入强度协方差矩阵给出了更具一般性的随机马赛克图像相似性度量指标. 所研究的相关系数在形式上更好地反映了图像的强度-几何特征间的关联性,且在特定的条件下,将Vizilter在文献[3]中的研究结果作为其特例. Vizilter在文献[3]中的实验测试表明在独立同分布的条件下相关系数在相似性度量的质量上具有优势,但对称系数在实际运用中对噪声表现出不稳定性. 而我们的工作对其在形式上进行了统一. [1]Pyt′ev Y P. Morphological image analysis[J].Pattern Recogn Image Anal, 1933(3): 19-28. [2]Evsegneev S O, Pyt′ev Y P. Analysis and recognition of piecewise constant texture images[J]. Pattern Recogn Image Anal, 2006, 16: 398-405. [3]Vizilter Y V, Zheltov S Y. Geometrical correlation and matching of 2D images shapes[J]. ISPRS Ann Photogramm Remote Sens Spatial Inf Sci, 2012, I-3: 191-196. [4]Vizilter Y V, Zheltov S Y. Projective morphologies and their application in structural analysis of digital images[J]. J Comput Syst Sci Int, 2008, 47: 944-958. [5]Vizilter Y V, Zheltov S Y. Similarity measure and comparison metrics for image shapes[J]. J Comput Syst Sci Int, 2014,53(4): 542-555. [6]Vizilter Y V, Gorbatsevich V S, Rubis A Y, et al. Shape-based image matching using heat kernels and diffusion maps[J]. Intenational Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, XL-3: 357-364.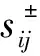
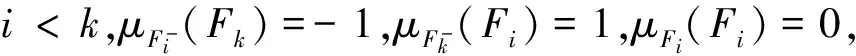
5 结束语
