双核因素蝙蝠算法

肖海军，成金华，何　凡

(1 中国地质大学(武汉) 数学与物理学院，武汉 430074；2中国地质大学(武汉) 经济管理学院 资源环境经济研究中心，武汉 430074)

1　研究背景

通过对生物行为的模拟，人们发现了均衡性强、优化效果好的群智能优化算法.受到群智能优化算法的启发，研究人员又提出了广泛应用的智能优化算法.如：随机扩散搜索[1]，蚁群优化[2]，粒子群优化[3,4]和蝙蝠算法[5].Bishop[1,6]提出的随机扩散搜索(SDS)是一种具有良好数学概率的全局搜索算法[7-9]，虽然在全局搜索过程中SDS效率高、鲁棒性好，但其优化技术只适用于可分解为多个部分函数的目标函数.蚁群优化算法[2](ACO)通过模拟“蚂蚁”记录位置和生物特征来寻找最优路径，这使得蚂蚁在后续的探索中找到更优的路径[10].但是ACO的最优解存在不确定性.粒子群优化算法(PSO)可以在n维空间中搜寻点或面的最优解[11-13]，该算法处理局部极值问题时灵活性较强.但是PSO算法需要大量的粒子群个体才能获得相对满意的优化结果.蝙蝠算法(BA)是Yang[5]提出的一种全局优化算法(蝙蝠通过模拟脉冲发射频率和响度来搜索猎物)，通过调整频率来加强解的多样性，并利用自动缩放能力来平衡寻优过程中的搜索与开发.

与其他算法相比，蝙蝠算法在处理一些复杂问题时表现更好.因此，一些研究人员有效地改进了蝙蝠算法.如：KHan等[14]提出了模糊逻辑蝙蝠算法，将模糊逻辑与蝙蝠算法相结合.Yang[15]提出了一种多目标蝙蝠算法来解决某些工程问题.Lin等[16]提出了组合蝙蝠算法，通过使用Lévy飞行和组合映射来估计算法参数.Nakamura等[17]提出名为二进制蝙蝠算法的离散版本来改进分类和特征选择.Xie等[18]提出了基于差分算子和Lévy飞行的蝙蝠算法，借此来解决优化问题.

此外，还有各种优化的蝙蝠算法.例如，Zhang和Wang[19]引入生物突变，来提高解决图像匹配多样性的问题.Xie和Zhou[20]提出了组合蝙蝠算法，通过组合蝙蝠算法与回声搜索来优化基准函数的数值.Fister I等[21]使用差分进化对蝙蝠路径进行局部搜索，然后结合四元数创建了四元数蝙蝠算法(QBA)，这种方法可以解决大规模的旋转型和几何计算型的优化问题[22].Li和Zhou[23]提出了一种基于复数编码的新型蝙蝠算法，它对编码的实部和虚部分别单独更新.

BA从搜索转向开发时收敛迅速，当频率、波长或响度变化太快时，可能导致局部最优.因此，本文提出一种改进的蝙蝠算法，称为双核因素蝙蝠算法(DCFBA).在DCFBA中，自适应速度更新公式加入了两个自适应学习因子并且受到最优和次优蝙蝠位置的影响，再通过仿真实验验证DCFBA的有效性.

2　蝙蝠算法

蝙蝠是一种具有回声定位能力的动物.搜索猎物时，蝙蝠发出的声波碰到一个物体后，声波会返回到它的耳中[13]，蝙蝠可以由此估计与物体的距离[24].基于蝙蝠回声定位的特性与狩猎习性，Yang[25]提出了标准蝙蝠算法，标准规则如下.

(1) 所有蝙蝠通过回声定位感知距离，并以某种独特的方式从背景障碍中区分猎物；

(2) 蝙蝠在位置Si以固定的频率fmin和速度vi，变化的波长λ和响度A0自由地狩猎；

(3) 假设响度从最大值A0到最小值Amin不等.

2.1　蝙蝠的速度更新和位置更新

fi=fmin+α(fmax-fmin),

(1)

(2)

(3)

其中α代表[0,1]中的随机数，fi表示当前时刻蝙蝠i的变化频率，Xbest是当前的全局最优解，可以通过比较所有解找到.

为了改善解的多样性，从蝙蝠群体中选择一只蝙蝠，并根据(4)式随机地产生一个新的局部解.通过此设置，局部搜索可以顺利进行，并从已经选择的解中精选新的解.

Xnew=Xold+δAt,

(4)

其中At表示此时所有蝙蝠的平均响度，δ∈[-1,1]是一个随机值，Xold代表从当前最优解中选择的随机解.

2.2　蝙蝠的响度更新和脉冲发射率更新

当搜索开始时，为了延长超声波传播的距离，将响度设置为最大值，将脉冲发射率设置为最小值.当蝙蝠搜索猎物时，响度逐渐降低，脉冲发射率增大，这可以帮助蝙蝠更准确地定位猎物.算法进行迭代时响度Ai和脉冲发射率ri的更新公式如下:

(5)

(6)

3　双核因素蝙蝠算法的速度更新方法及步骤

速度更新公式在蝙蝠算法中起关键作用，它决定了蝙蝠在搜索空间的速度.蝙蝠算法通过(2)式更新蝙蝠的速度，它考虑到以前的速度和当前蝙蝠的最佳位置.然而，蝙蝠的最佳位置并不是改变搜索方向的唯一因素.我们在研究过程中发现蝙蝠的次优位置也是影响优化结果的一个重要因素.因而在提出的DCFBA中我们考虑了这个因素，这种改进的蝙蝠算法称之为双核因素蝙蝠算法(DCFBA).

3.1　DCFBA的速度更新方法

(7)

其中Xbest和Xsecond分别代表其他蝙蝠的最优位置和次优位置，c1(t)和c2(t)为学习因子.更新公式如下：

c1(t)=1-exp(-Ψ(t)),

(8)

c2(t)=1-c1(t),

(9)

Ψ(t)=|Fitnessmean(t)-Fitnessbest(t)|,

(10)

(11)

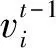
依靠速度更新公式的创新，可以大大加强DCFBA在优化过程中的灵活性，使算法具有提高收敛速度的优点，更重要的是可以避免算法陷入局部最优.

3.2　DCFBA的更新方法

基于上述更新规则，DCFBA的实施步骤可概括如下.

DCFBA伪代码Input：M：thepopulationsizeofbatsε：theloudnessγ：thepulseemissionfmax：themaximumpulsefrequencyfmin：theminimumpulsefrequencyitermax：themaximumnumberofiterationsOutput：thebatwiththebestfitnessvalueinthepopulation．Initialisethebats′positionsXi，velocityvi，frequencyfi，pulseratesriandtheloudnessAi．Assumethefitnessfunctionisminimum．whilethestopconditionisnotsatisfieddo　　forallbatsdo　　CalculatethefitnessvalueFitnessiandobtainthebestsolutionbyupdatingthebats′positionsandvelocityasdescribedinEqu．(3)and(7)．　　ifrand>rithen　　　ChooseasolutionamongthebestonesandrandomlygeneratealocalsolutionXnewaroundthebestchosensolution．　　endif　　EvaluatenewsolutionFitnessnew　　ifrand

4　数值验证

4.1　基准问题

在实验中，为了研究DCFBA的有效性、效率性和稳定性，我们采用BA和PSO算法作为对比算法，选取了具有不同属性的9个基准优化函数.这9个基准函数可以分为高维单峰函数(第I类)、高维多模态函数(第II类)和低维函数(第III类)，见表1.

表1　基准优化函数Tab.1　Benchmark functions

4.2　仿真平台

用于评估DCFBA的平台的配置为：Intel Pentium(R)双核CPU，2.5GHz，2.00GB RAM，Windows 7操作系统，MATLAB 2014a(Windows)开发环境.

4.3　参数设置

在DCFBA算法中蝙蝠群体大小为20，响度衰减系数α=0.5，增加脉冲发射系数γ=0.5，脉冲频率fi∈[0,2].BA算法的参数与DCFBA相同.在PSO算法中学习因子c1=c2=0.5，粒子群体大小为30.

4.4　实验结果

采用3种方法在9个基准函数上的优化对比结果如表2～4所示.其中Worst，Mean，Best和Std.分别表示最差适应度值，平均适应度值，最佳适应度值和适应度值的标准差.黑体数字表示DCFBA是优选的，而加下划线的数值表示其他算法是优选的.

由表2可知，DCFBA可以在第I类函数中获得最优结果.对于这4个函数，DCFBA的最差适应度值，平均适应度值，最佳适应度值和适应度值的标准差均优于BA和PSO，这意味着DCFBA在高维单峰函数下具有最佳的稳定性.

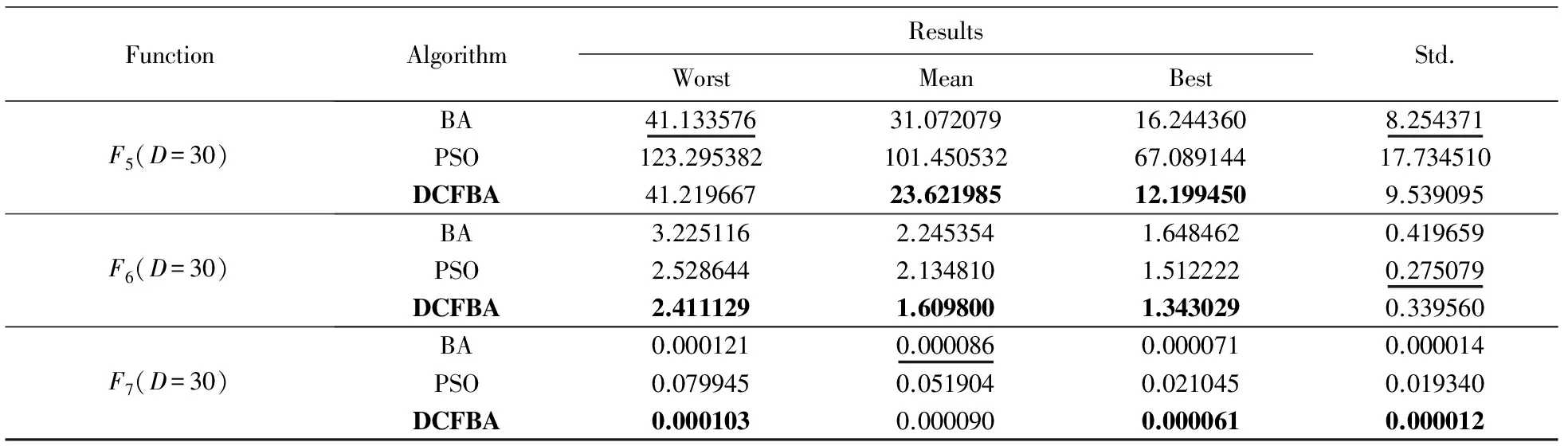
表3　函数F5,F6,F7的仿真结果Tab.3　Simulation results for test functions F5,F6,F7

由表3可知，DCFBA在第Ⅱ类函数中的优化结果也是最好的.即便DCFBA在某项指标上不如其他算法，但其结果也是非常接近最优值的.总体而言，DCFBA在高维多峰函数上的优化性能优于BA和PSO.

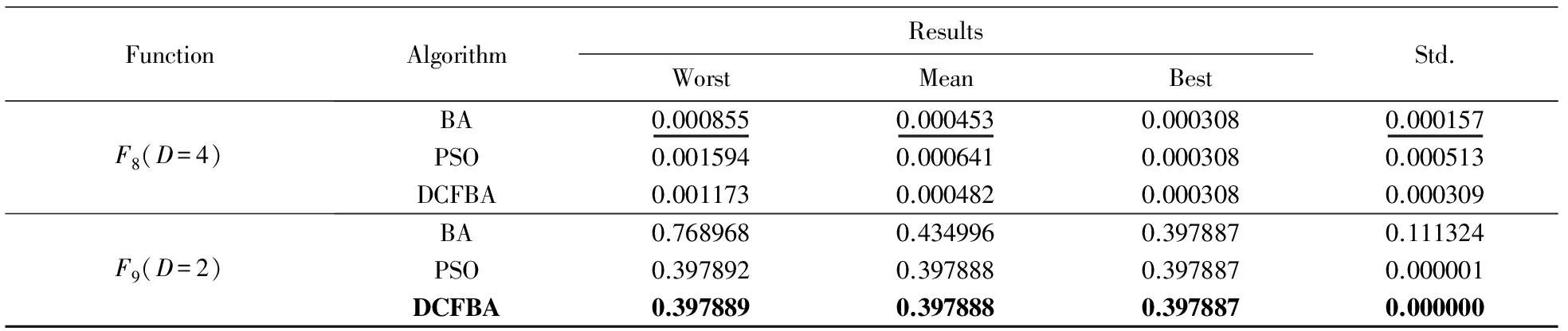
表4　函数F8, F9的仿真结果

由表4可知，对于函数F8，3种算法的最优适应度值相等，虽然DCFBA在平均适应度值和标准偏差上比BA稍差，但是DCFBA的其他指标都比BA和PSO好.对于F9，DCFBA优于(超过或等于)BA和PSO的结果.显然，在第Ⅲ类函数上，DCFBA的性能仍然优于BA和PSO.

针对三类函数，图1～9是适应性演化曲线，函数F1，F2，F3，F5，F7和F8的迭代次数从10变化到810.图4对应的函数F4迭代次数为1110，图9对应的函数F9迭代次数为325.函数F1～F9的维度D设置为30，蝙蝠群体m为20，搜索步长为0.01.算法经过十折交叉验证后的结果表明：DCFBA在所有基准函数上的优化结果优于BA和PSO算法.

图1　F1适应度值演化曲线，搜索范围为[-100,100] Fig.1　Evolution curves of fitness value for F1,bounds ∈[-100,100]

图2　F2适应度值演化曲线，搜索范围为[-100,100]Fig.2　Evolution curves of fitness value for F2, bounds∈[-100,100]

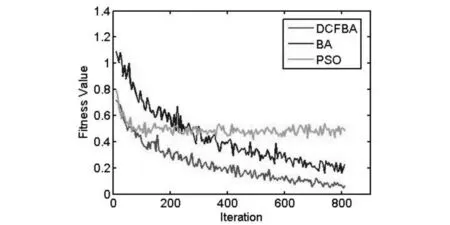
图3　F3适应度值演化曲线，搜索范围为[-100,100]Fig.3　Evolution curves of fitness value for F3,bounds∈[-100,100]

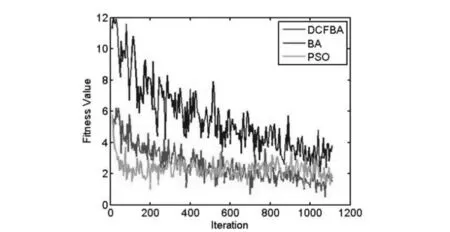
图4　F4适应度值演化曲线,搜索范围为[-100,100]Fig.4　Evolution curves of fitness value for F4, bounds∈[-100,100]

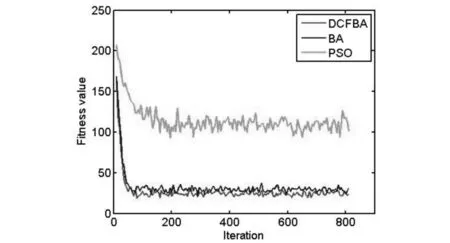
图5　F5适应度值演化曲线，搜索范围为[-100,100] Fig.5　Evolution curves of fitness value for F5, bounds∈[-100,100]

图6　F6适应度值演化曲线，搜索范围为[-32,32] Fig.6　Evolution curves of fitness value for F6,bounds∈[-32,32]

图7　F7适应度值演化曲线，搜索范围为[-100,100]Fig.7　Evolution curves of fitness value for F7,bounds∈[-100,100]

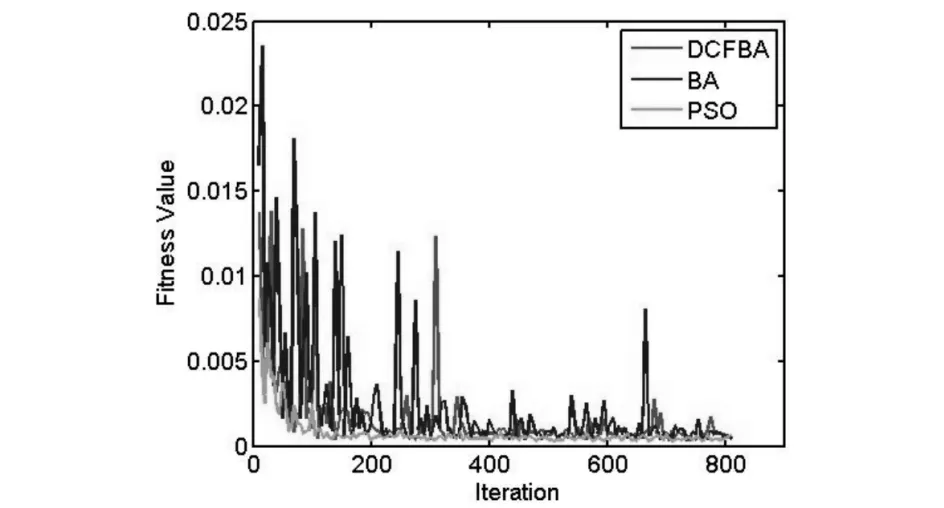
图8　F8适应度值演化曲线，搜索范围为[-5,5]Fig.8　Evolution curves of fitness value for F8, bounds∈[-5,5]

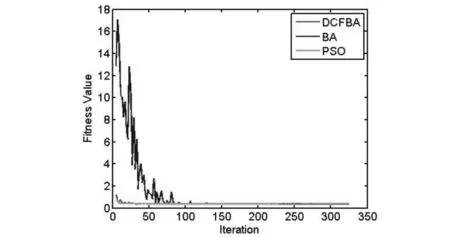
图9　F9适应度值演化曲线，搜索范围为[-5,15]Fig.9　Evolution curves of fitness value for F9,bounds∈[-5,15]

5　结语

本文提出了一种新的改进蝙蝠算法——双核因素蝙蝠算法.通过3种算法在9个基准函数的仿真实验表明DCFBA有效可行.虽然在实验中，DCFBA算法有比其他两种算法更好的收敛速度，但在一些迭代中是不稳定的.作为一个优秀的优化算法，DCFBA可以尝试与其他优化算法结合，这可能会改善其优化性能.此外，DCFBA参数设置的合理性、函数维度设置对DCFBA的影响等，值得进一步研究.

[1]Bishop J M. Stochastic searching networks[C]//IEEE. 1989 First IEEE International Conference on IEEE. California: IEEE, 1989:329-331.

[2]Dorigo M. Optimization, learning and natural algorithms[D]. Milano: Politecnico di Milano Italy, 1992.

[3]Kennedy J, Eberhart R. Particle swarm optimization[C]//IEEE. IEEE International Conference on Neural Networks Proceedings(IEEE 4). New York: IEEE, 2002:1942-1948.

[4]Shi Y, Eberhart R. A modified particle swarm optimizer[M]. IEEE. IEEE International Conference on Evolutionary Computation. Anchorage: IEEE,1998: 69-73.

[5]Yang Xinshe. A new metaheuristic bat-inspired algorithm[J]. Computer Knowledge and Technology, 2010, 284:65-74.

[6]Nasuto S, Bishop J M. Stabilizing swarm intelligence search via positive feedback resource allocation[M]. Berlin, Heidelberg: Springer, 2008:115-123.

[7]Nasuto S, Bishop J M, Lauria S. Time complexity analysis of the stochastic diffusion search[M]. Berlin, Heidelberg: Springer, 1998: 260-266.

[8]Nasuto S, Bishop J M. Convergence analysis of stochastic diffusion search[J]. Parallel Algorithms and Applications,1999, 14(2):89-107.

[9]Myatt D R, Bishop J M, Nasuto S. Minimum stable convergence criteria for stochastic diffusion search[M]. Berlin, Heidelberg: Springer, 2004, 40(2):112-113.

[10]Parsons S. Ant Colony Optimization by Marco Dorigo and Thomas Stützle[J]. Knowledge Engineering Review, 2005, 20(1):92-93.

[11]Griffin D R, Webster F A, Michael C R. The echolocation of flying insects by bats[J]. Animal Behaviour, 1960, 8(3):141-154.

[12]Parsopoulos K E, Vrahatis M N. Recent approaches to global optimization problems through particle swarm optimization[J]. Natural Computing, 2002, 1(2-3): 235-306.

[13]Clerc M. The swarm and the queen:Towards a deterministic and adaptive particle swarm optimization[C]// IEEE. Proceedings of the Congress on Evolutionary Computation. Piscataway, NJ: IEEE Service Center, 1999: 1951-1957.

[14]Khan K, Nikov A, Sahai A. A fuzzy bat clustering method for ergonomic screening of office workplaces[C]//AINSC. Third International Conference on Software, Services and Semantic Technologies S3T 2011. Berlin, Heidelberg: Springer, 2011:59-66.

[15]Yang X. Bat algorithm for multi-objective optimisation[J]. International Journal of Bio-Inspired Computation, 2011, 3(5):267-274.

[16]Lin J H, Chou C W, Yang C H, et al. A chaotic Lévy flight bat algorithm for parameter estimation in nonlinear dynamic biological systems[J]. ResearchGate, 2012, 2(2):56-63.

[17]Nakamura R Y M, Pereira L A M, Costa K A, et al. BBA: A binary bat algorithm for feature selection[J]. Graphics, Patterns and Images, 2012(1): 291-297.

[18]Xie J, Zhou Y, Chen H. Anovel bat algorithm based on differential operator and Lévy flights trajectory[J]. Computational Intelligence and Neuroscience, 2013(2013):38-45.

[19]Zhang J W, Wang G G. Image matching using a bat algorithm with mutation[J]. Applied Mechanics and Materials, 2012, 203(1):88-93.

[20]Xie J, Zhou Y. A novel hybrid bat algorithm with harmony search for global numerical optimization[J]. Journal of Applied Mathematics,2013(3):233-256.

[21]Fister I, Fister D, Yang X S. A hybrid bat algorithm[J]. Electrotechnical Review,2013, 80(1): 64-73.

[22]Fister I. Using the quaternion′s representation of individuals in swarm intelligence and evolutionary computation[J]. Computer Science, 2013(1):34-47.

[23]Li L, Zhou Y. A novel complex-valued bat algorithm[J]. Neural Computing and Applications,2014, 25(6): 1369-1381.

[24]Metzner W. Echolocation behaviour in bats[J]. Science Progress, 1991, 75:453-465.

[25]Yang X S, Deb S. Eagle strategy using Lévy walk and firefly algorithms for stochastic optimization[J]. Studies in Computational Intelligence,2010, 284:101-111.