中国波指与50ETF波动性——基于已实现波动率的研究

(武汉大学经济与管理学院　湖北　武汉　430072)

一、引言

一直以来，资产收益率的未来波动是进行资产定价、资产配置和风险管理的重要参考变量。预测标的资产未来的波动率通常有两种方式，第一是通过各种统计模型，基于模型对未来的波动率进行预测；第二是通过在公开市场上进行交易的期权，由期权价格反推出未来的波动率。

在基于模型的波动率预测方面，Glosten(1993)提出非对称的GJR-GARCH模型，在此基础上，Blair(2001)将已实现方差引入模型，提出了GJR-RV模型。模型预测方面除了GARCH模型外还有随机方差SV模型，SV模型与GARCH模型的不同之处在于条件方差不再是过去收益率的函数，而是遵循自身的随机路径。Corsi(2004)在市场假说的理论基础之上，提出了HAR-RV模型，Anderson(2007)在HAR-RV模型的基础上，将已实现波动率划分为连续波动和跳跃波动，提出HAR-RV-J模型，国内学者李洋(2012)等也对HAR模型进行了进一步的改进。在隐含波动率方面，1993年芝加哥期权期货交易所推出第一支VIX指数，目前的隐含波动率指数包括跟踪标普500的VIX,跟踪纳斯达克100的VXN,跟踪道琼斯工业指数的VXD。2016年11月28日，上交所正式发布了上证50ETF波动率指数(iVX)。

由于iVX上线时间较短，与国内外众多对VIX指数的研究如Becker等(2007)、吴鑫育和周海林(2014)等的研究相比，国内学者在基于高频数据分析50ETF期权隐含波动率信息内涵这一方面的研究，仍属于空白。本文的研究基于非参数估计的方法，得到了整体波动和跳跃风险的准确刻画，探讨了iVX与未来跳跃之间的关系，将有助于加深市场参与者对于期权交易市场运行微观结构的认识，增强市场参与者与监管者的风险预测和控制能力，有利于促进中国金融市场的繁荣稳定发展。

二、数据

本文选取上证50ETF的1分钟数据作为研究对象，用于计算50ETF的已实现双幂次变差和已实现跳跃变差，样本区间为2015年2月9日至2016年11月16日共429个交易日，102720个样本数据，数据来源于Wind数据库；期权隐含波动率选取同期的中国波指(iVX)作为研究对象，中国波指是由上海证券交易所发布，用于衡量上证50ETF未来22个交易日的预期波动。该指数是根据方差互换的原理，结合50ETF期权的实际运作特点，并通过对上海证券交易所交易的50ETF期权价格的计算，编制而得，iVX数据来源于上交所官网。样本区间内的iVX数据的统计性描述见下表1。

三、已实现波动率的测量

假设50ETF的对数价格st=log(St)服从如下跳跃扩散过程：

dst=μtdt+σtdWt+Jtdqt

(1)

其中，μt和σt分别为漂移项和扩散项，Wt是标准布朗运动，dqt是泊松跳跃过程，当发生跳跃时dqt为1，否则为0。

Anderson等(2001)证明了在不存在跳跃和市场微观噪音的情况下，根据日内高频收益率的平方和求得的已实现方差(简称RV)是积分方差的一致估计量。Bandorff-Nilsen等(2004)在引入跳跃的情况下，提出了已实现双幂次变差(简称BV)，他们证明，在资产价格存在跳跃时，当采样频率足够高时，

(2)

(3)

因此，RV与BV的差值J即为跳跃部分的一致估计。Anderson等(2007)进一步提出跳跃检验统计量:

(4)

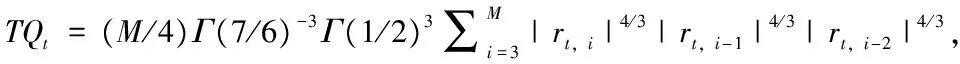
表2给出了各个变量的描述性统计，由表可知，已实现波动率的连续部分和跳跃部分的均值分别为0.000346和0.000091，跳跃波动相对于连续波动占比较小，连续波动构成了每个交易日波动的主要部分。跳跃波动显著的次数为273个交易日，占样本区间的63.6%，可见，已实现波动率发生跳跃的频率非常高，这可能与样本区间发生了多次股灾有关。由RV，BV，J的偏度和峰度可知，三者均呈现右偏，尖峰现象。

表2　波动率的描述性统计

注：***、**和*分别代表在1%、5%和10%的显著性水平上显著(下同)。

四、基于模型的波动率预测—HAR-RV-CJ模型

HAR-RV模型由Corsi(2004)提出，其基本思想源自于异质市场假说，该假说认为，交易者是异质的，异质的原因可能来源于信息差异、持有期不同等，短线投资者按天进行交易，基金经理按周调整头寸，而社保基金等可能持有期更长，由于交易者的异质性使得波动成分包含有不同类型。Corsi(2004)按日、周、月将波动分为三类，提出了HAR-RV模型。

HAR-RV模型虽然刻画了已实现波动率的长记忆性，但是它没有对连续波动和跳跃波动进行划分，从而区别对待，Anderson(2007)在HAR-RV模型的基础上，将已实现波动率划分为连续波动和跳跃波动，对二者区别对待，引入跳跃波动作为未来波动率的自变量，提出了HAR-RV-J模型。HAR-RV-CJ模型如下：

RVt,t+22=β0+β1BVt+β2BVt-5,t+β3BVt-22,t+β4Jt+β5Jt-5,t+β6Jt-22,t+εt,t+22

(5)

表3　HAR模型估计结果

实证结果如上表3所示。由回归结果可知，连续波动的日效应、周效应和月效应均显著为正，并且日效应和月效应在1%的置信水平下显著，周效应在10%的置信水平下显著，表明50ETF对于连续波动具有很强的记忆性。其中，日效应的估计值最高，表明市场波动对于日波动率的记忆性最强，其次是月效应和周效应。根据异质市场假说，日效应、周效应和月效应分别对应短线交易者、基金经理和长线交易者的交易行为，由回归分析可知，在中国50ETF市场上，三种异质交易者均存在，并且进行短线投机的交易者对于市场波动率的影响最大，这与中国证券市场的现实是一致的。从表3可知，跳跃波动的日效应和周效应均不显著，而月效应显著为负，且估计值最高，表明50ETF市场的已实现波动率具有很强的均值回复效应，这可能是因为跳跃波动能迅速的释放交易者对未来市场的情绪或预期，从而使未来的波动率下降。

五、iVX与未来跳跃波动

iVXt=α+βρt+εt

(6)

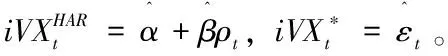
iVXt=α+βρt+γRVt+εt

(7)

GMM模型的回归结果如下表4。

表4　未来跳跃波动的GMM模型回归结果

从回归结果可以看出，对于50ETF未来跳跃波动的日效应，J统计量均不显著，意味着在对于未来一天的跳跃波动的预测上，iVX并不包含HAR-RV-J模型之外的额外的对未来跳跃波动的预测能力，而随着预测周期的延长，J统计量逐渐变得显著，对于未来跳跃波动的周效应，J统计量在10%的置信水平上显著，而对于月效应，J统计量在1%的置信水平上显著，这表明，在对于50ETF未来跳跃波动的长周期预测上，iVX中包含了HAR-RV-J模型以外的关于未来跳跃波动的信息，具有比HAR-RV-J模型更为优秀的预测能力。产生这种现象的可能原因是,一方面iVX本身就是对未来22个交易日的波动预测，另一方面，对于跳跃波动的测量随着周期的延长而变得更为精确。GMM模型中对于月效应的估计，Adj R2出现负数，可能是因为工具变量的选择使得矩条件强烈不成立，进而GMM模型估计出参数出现较大偏差，从而残差的平方和大于因变量的方差。

六、结语

一直以来，期权的隐含波动率都吸引了国内和国际大量学者的目光。iVX是中国首支隐含波动率指数，对于它的研究，有利于我们更好的认识和理解金融市场的运行过程。本文借助50ETF现货市场的高频数据，利用非参数估计的方法计算每日的连续波动和跳跃波动，并进一步考察iVX与50ETF过去跳跃波动信息和未来跳跃波动信息之间的关系。

研究结果表明：(1)采用HAR-RV-J模型发现连续波动的日效应最强，其次是月效应和周效应，三者均显著为正。这表明在中国50ETF市场上，三种异质交易者均存在，并且进行短线投机的交易者对于市场波动率的影响最大。跳跃波动仅具备显著为负的月效应，且估计参数最大，表明50ETF市场的已实现波动率具有很强的均值回复效应，本期急剧的跳跃波动有利于下一期波动率的下降。(2)采用GMM模型对iVX与未来跳跃波动的研究表明，与基于HAR模型的波动率预测相比，iVX包含了更多的对长周期的未来跳跃波动的预测信息。

综上，我们认为，iVX作为一个由市场交易所决定的对未来波动率的预测指数，有助于市场参与者更好地认识和分析股票市场的波动风险和跳跃风险。iVX的实时更新性与对未来波动良好的预测能力，有利于投资者进行更佳的风险管理，也为维持金融市场的稳定繁荣提供了有效的参考依据。

【参考文献】

[1]李洋和乔高秀，2012，《沪深300股指期货市场连续波动与跳跃波动——基于已实现波动率的实证研究》，《中国管理科学》第1期，第451-458页。

[2]吴鑫育和周海林，2014，《波动率风险溢价——基于VIX的实证》，《系统工程理论与实践》第一期，第1-11页。

[3]Andersen T G,Bollerslev T,Diebold F X,et al.,2001,”The Distribution of Realized Stock Return Volatility”,Journal of Financial Economics,61(1):43-76.

[4]Andersen T G,Bollerslev T,Diebold F X,2007,”Roughing It Up:Including Jump Components in The Measurement,Modeling,and Forecasting of Return Volatility”,The Review of Economics and Statistics,89(4):701-720.

[5]Barndorff-Nielsen O E,Shephard N,2004,”Power and Bipower Variation with Stochastic Volatility and Jumps”,Journal of Financial Econometrics,2(1):1-37.

[6]Becker R,Clements A E,White S I,2007,”Does Implied Volatility Provide Any Information Beyond that Captured in Model-Based Volatility Forecasts?”,Journal of Banking & Finance,31(8):2535-2549.

[7]Blair B J,Poon S H,Taylor S J,2010,”Forecasting S&P 100 Volatility:The Incremental Information Content of Implied Volatilities and High-Frequency Index Returns”,Handbook of Quantitative Finance and Risk Management.Springer US,1333-1344.

[8]Chernov M,2007,”On The Role of Risk Premia in Volatility Forecasting”,Journal of Business & Economic Statistics,25(4):411-426.

[9]Corsi F,2004,”A Simple Long Memory Model of Realized Volatility”,Available at SSRN 626064,2004.

[10]Glosten L R,Jagannathan R,Runkle D E,1993,”On the Relation Between The Expected Value and The Volatility of The Nominal Excess Return on Stocks”,The Journal of Finance,48(5):1779-1801.