An improvement of soil temperature simulations on the Tibetan Plateau

SiQiong Luo , BoLi Chen , ShiHua Lyu , XueWei Fang , JingYuan Wang ,XianHong Meng , LunYu Shang , ShaoYing Wang , Di Ma

1. Key Laboratory of Land Surface Process and Climate Change in Cold and Arid Regions, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou, Gansu 730000, China

2. Changzhou Meteorological Bureau, Changzhou, Jiangsu 213000, China

3. School of Atmospheric Sciences, Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology, Chengdu, Sichuan 610225, China

4. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing, Jiangsu 210044, China

1　Introduction

The Tibetan Plateau (TP), with an average elevation of more than 4,000 m above sea level, is the highest and most extensive plateau in the world; it is known as the "roof of the world" (Liu and Chen,2000). Many studies have provided strong evidence that the TP exerts profound thermal and dynamic effects on the local weather and climate, as well as on atmospheric circulation in the Northern Hemisphere(Yeh and Gao, 1979; Manabe and Broccoli, 1990).The simulation of soil temperature and moisture on the TP plays a dominant role in the performance of both global climate and numerical weather forecast models. Studies have shown that accurate prediction of soil temperature and moisture is critical for predicting convection, clouds, air temperature, and moisture at various temporal and spatial scales (Avissar and Pielke, 1989; Findellet al., 2009; Bhattacharya and Mandal, 2015). Permafrost and seasonally frozen ground exist extensively on the TP, and their seasonal freeze-thaw processes and spatial distribution lead to variations in the surface moisture conditions and energy balance. The freeze-thaw processes are a buffer to the seasonal changes in soil and near-surface temperatures and strengthen the energy exchange between the soil and the atmosphere (Chenet al.,2014b). Neglecting frozen ground processes results in a significant underestimation/overestimation of soil temperature during soil freezing-thawing periods and underestimation of total soil moisture content after extensive periods of soil freezing (Korenet al., 1999).

Soil thermal conductivity is one of the key thermal properties in numerical models utilized to determine soil temperature and soil heat flux (Gaoet al., 2003;Gao, 2005). It is also a parameter that is difficult to estimate. Soil thermal conductivity depends on the volumetric water content of soil and is related to mineral composition (especially quartz content), porosity, dry density, and temperature (Farouki, 1986; Peter-Lidardet al., 1998). On the TP, the soil genetic layer is shallow and contains large soil particles and a high content of broken stones and gravel in local areas.Abundant permafrost and seasonally frozen soil also exist on the surface of the TP. Given that the thermal conductivity of ice is four times that of water, soil thermal conductivity changes significantly with the change in soil freezing or thawing, as well as in soil water and ice contents (Yoshikawaet al., 2002; Overduinet al., 2006). So it is very difficult to parameterize correctly the soil thermal conductivity on the TP.

Johansen (1975) utilized some of the data provided by Kersten for medium and fine sands and fine-grained soils and developed a thermal conductivity parameterization scheme to predict soil thermal conductivity. This parameterization scheme normalizes actual thermal conductivity data with respect to the thermal conductivity of dry and saturated fine soils and sands; the scheme addresses the effect of mineral content through the thermal conductivity of solid particle sand, as well as the effect of the degree of saturation and grain size distribution, through empirical relationships (Peter-Lidardet al., 1998; Côté and Konrad, 2005b). Farouki reviewed the calculation method for soil thermal conductivity comprehensively and pointed out that the unfrozen water present in frozen fine-grained soils plays an important and effective role in facilitating heat transfer(Farouki, 1981). He compared eleven semi empirical methods and found that Johansen's modified method performs best in calculating sand and fine soil thermal conductivity in both frozen and unfrozen sates(Farouki, 1986). This parameterization method is widely utilized in present land surface process models, such as the Common Land Model (CoLM) and the Community Land Model (CLM). Luoet al. collected soil samples from 16 plots on the TP and found large soil particles and a high content of broken stones and gravel in the soil (Luoet al., 2009b). After analysis, they concluded that Farouki's soil thermal conductivity parameterization scheme provides a significant overestimation for the TP and pointed out that Johansen's scheme is better than others (Luoet al.,2008, 2009b).

In the current study, Johansen's scheme was introduced into the Community Land Model 3.5(CLM3.5). This improved model was utilized for oneyear offline numerical simulation of the Zoige Station, which is a long-term observation and research station supported by the Chinese Academy of Sciences.Observation data and simulated soil temperature and moisture values from the original thermal conductivity parameterization scheme and the modified scheme were compared to improve the results for soil temperature and moisture. Afterward, Johansen's scheme was introduced into the Regional Climatic Model 4(RegCM4) coupled with CLM3.5 (RegCM4-CLM3.5),which was employed to simulate the entire TP. Observation data and simulated soil temperature were also compared over the entire TP to determine how the model improves soil temperature estimation.

2　Models and experimental design

2.1　Brief introduction of models

CLM is a land surface process model issued by the National Center for Atmospheric Research(NCAR) and is the land surface module of the Community Climate System Model. It incorporates the advantages of the Biosphere-Atmosphere Transfer Scheme (BATS), Institute of Atmospheric Physics,the Chinese Academy of Sciences land model(IAP94), and the NCAR land surface model. The model has three parts. The first part includes a biogeophysical process, which mainly describes energy, water, and momentum exchanges in the earth-atmosphere system. Parameterization of radiation flux,soil hydrothermal properties, and physical properties of snow cover is also introduced in this process. The second part is a biogeochemical process, which mainly introduces exchanges of chemical components in the earth-atmosphere system, including biological flux exchange, carbon and nitrogen cycles, and dynamic vegetation. The third part is a water cycle process that mainly describes vegetation canopy interception, surface and subsurface runoffs, soil water storage and infiltration, and so on. Compared with CLM3.0, the modifications in CLM3.5 are as follow:new surface datasets and parameterizations, such as surface datasets based on moderate resolution imaging spectroradiometer (MODIS) products (Lawrence and Chase, 2007); an improved canopy integration scheme (Thornton and Zimmermann, 2007); a simple TOPMODEL based model for surface and subsurface runoff (Niuet al., 2005); water table depth determination by a simple groundwater model (Niuet al.,2007); and the concept of supercooled soil water through implementation of a freezing point depression equation and relaxed dependence of hydraulic properties in the soil ice content by incorporating the fractional impermeable area to modify the frozen soil scheme (Niu and Yang, 2006). More details are available in the CLM Manual (Vertensteinet al., 2004)and Technical Documentation (Olesonet al., 2004).The performance of difference versions of CLM has been confirmed on the TP (Chenet al., 2012a, 2014a,2014b; Xionget al., 2014; Fanget al., 2016).

RegCM is a regional climatic model developed by NCAR and then improved by the International Center for Theoretical Physics. With its high temporal-spatial resolution, good capability to capture small system change information, and good simulation of local climatic features caused by constraints, RegCM is one of the relatively mature regional climatic models. It employs the MM5 dynamic framework,σcoordinates on the vertical axis, and Arakawa B staggered grids on the horizontal axis. Its main physical processes include a radiation process, land surface process, boundary-layer scheme of planets, cumulus convective precipitation scheme, large-scale precipitation scheme, and barometric gradient scheme. RegCM covers a total of six lateral boundary treatment plans,namely, fixed, linear loose, time correlation, time change and in-out, sponge, and exponential loose boundaries. The model outputs the physical parameters of over 40 processes, including atmosphere, land surface, and radiation processes. Compared with RegCM3, the new RegCM4 is coupled with the land surface process of CLM3.5 and maintains the original land surface model BATS as an optional choice for users. Further modifications were made on the planet boundary-layer and radiation transfer plans. More details can be found in the RegCM Manual (Giorgi and Elguindi, 2011) and Technical Documentation (Elguindiet al., 2011). The performance of the previous version of RegCM has been evaluated on the TP, and results show that RegCM has the ability to simulate the basic character of the spatial distribution of precipitation and air temperature over the TP (Zhanget al., 2005).

2.2　Thermal conductivity parameterization in models

Thermal conductivity parameterization in CLM3.5 is mainly based on the research of Farouki (Farouki,1986). Thermal conductivityλ(W/(m·K)) is expressed as

whereλsatandλdryare soil thermal conductivities under saturation and dry conditions, respectively;Keis the Kersten number; andSris the wetness of the soil with respect to saturation. Thermal saturated soil conductivityλsat(W/(m·K)) is determined by thermal conductivities of soil solids, liquid water, and ice constituents as follows:

whereTfis the freezing point temperature;θsatis the volumetric water content at saturation (porosity);θlipis the liquid water content of soil;λliq= 0.57 W/(m·K)andλice= 2.29 W/(m·K) are the thermal conductivities of water and ice, respectively; andλsis the mineral soil solid thermal conductivity. The thermal conductivity of the mineral soil solid is determined by soil texture as follows:

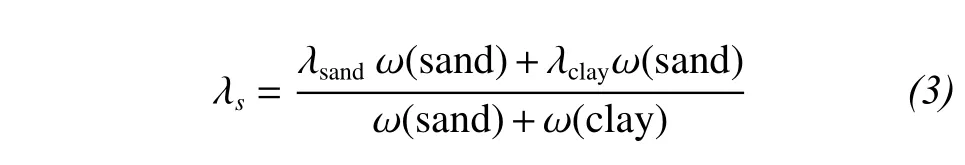
whereλsand= 8.8 W/(m·K) andλclay= 2.29 W/(m·K)are the thermal conductivities of sand and clay,respectively; ω(sand) and ω(clay) are the percentage contents of sand and clay, respectively. The thermal conductivity of dry soil in Equation(1)is determined by bulk densityρd=2700(1-θsat) as

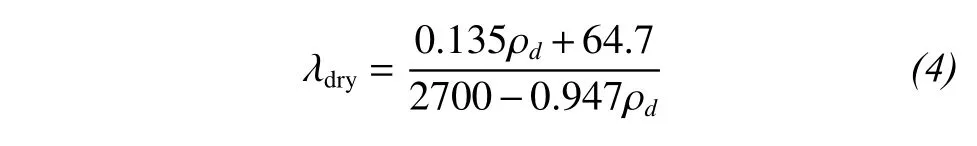
The Kersten number is a function of the degree of saturationSrand the phase of water.

2.3　Improvement of thermal conductivity parameterization

Among existing calculation methods of soil thermal conductivity, Johansen's scheme (Johansen,1975) is one of the highly appreciated methods. In addition, Farouki's method was developed from Jo-hansen's scheme. Recently, Côté (Côté and Konrad,2005b), Luet al. (Luet al., 2007), and Luo (Luoet al., 2009b) improved their scheme according to Johansen's to provide a more accurate calculation of soil thermal conductivity. Thermal conductivity calculation of mineral soil solidλsis the main difference between Johansen's scheme and Farouki's. In Johansen's scheme, the thermal conductivity of mineral soil solid is calculated according to the content and thermal conductivity of quartz as follows:

whereλq= 7.7 W/(m·K) is the thermal conductivity of quartz,λo= 2.0 W/(m·K) is assigned to all the other forming minerals, andδis the quartz content that corresponds to 50% of the sand content (Peter-Lidardet al., 1998; Sun, 2005; Luoet al., 2009b).

The depth and thickness of soil layers, node depth,the composition of soil layers at the Zoige Station,and the thermal conductivity of mineral soil solid calculated with Farouki's and Johansen's schemes are listed in Table 1. The mean thermal conductivity of a 10-layer mineral soil solid calculated with Farouki's scheme is 7.28 W/(m·K), whereas that calculated with Johansen's is significantly smaller (2.69 W/(m·K)).The thermal conductivity of solid particles generally varies from 1 W/(m·K) to 5 W/(m·K) (Côté and Konrad, 2005a). This result indicates that the thermal conductivity of mineral soil solid at the Zoige Station calculated with the thermal conductivity parameterization scheme of Farouki in the CLM3.5 model is significantly higher than that calculated with Johansen's(approximately three times higher).

Table 1　Depth and thickness of soil layers, node depth, composition of soil layers at the Zoige Station; and thermal conductivity of mineral soil solid calculated with Farouki's scheme and Johansen's scheme

2.4　Experiments

For the control experiment, offline and regional simulation experiments were conducted on the TP with CLM3.5 and the coupled model (RegCM4-CLM3.5);these experiments are hereafter referred to as the CTRL experiment. The description of the experiments is showed in Table 2. The offline experiment employed atmospheric forcing data from the Zoige Station; and the simulation time was from July 1,2009, to July 31, 2010. Zoige Station, which was founded in 2005, is located in the northeast part of the TP. Generally, the climate at this site is cold and damp, with wet, mild summers and dry, cold winters.The annual mean temperature is 1.9 °C; and the annual mean precipitation value from 1981 to 2010 is 593 mm, according to the climate data measured at a meteorological station (34°00′N, 102°08′E, altitude 3,471 m) located approximately 14 km north of the Zoige site. Vegetation in this area is typical alpine meadow, with a canopy height of 0.20 m in summer and 0.10 m in winter. Atmospheric input variables required in the CLM3.5 model to conduct the offline experiment included air temperature, wind speed, humidity, air pressure, rainfall rate, and downward shortwave radiation. The first three variables utilized the data of the observation tower at 10.13 m. The time step in the model was set to 30 min. Soil composition,which is closely related to soil temperature and humidity, was established by referring to references on soil samples at the Zoige Station (Luoet al., 2009a).Other surface parameters employed the initial values of the model. For a more intuitive comparison between simulated and observed soil temperature and humidity values, the simulated results were introduced into the layer of the observed results through linear interpolation.

The integral time in the regional simulation experiment was six years (January 1, 1995, to December 31, 2000). The first year was regarded as the spin-up period of the model, which was eliminated during result analysis. The central point of the model was determined as 33°N, 89°E. The grid numbers south to north and east to west were 56 and 96, respectively. The horizontal resolution was 45 km. The simulation scope covered the TP and its surrounding regions. The model has 18 layers vertically, and the air pressure on the top layer was 5 hPa. The integral time step was 150 s. Data used in the model were provided by the official website of RegCM4(http://www.ictp.it/research/esp/models/regcm4.aspx).Here, a brief review follows. The terrain of the model was obtained through interpolation of 10′×10′ (longitude×latitude) terrain data of the United States Geological Survey (USGS). The vegetation cover data utilized Global Land Cover Characterization (GLCC)data remotely retrieved by USGS through satellites.The initial field and subsequent boundary values were acquired from ERA40 reanalysis data of the European Center of Medium Range Weather Forecasts. Sea temperature data adopted the weekly analysis data OI_WK of the National Oceanic and Atmospheric Administration. The land surface process employed the CLM3.5 model, and the physical parameter output frequency of the land surface process was set to 12 h.

Table 2　Description of the control and sensitivity experiments

For the sensitivity experiment, the calculation formula of mineral soil solid in CLM3.5 was replaced by that in Johansen's scheme; that is, Equation(3)was replaced by Equation(6). Offline and regional simulation experiments were conducted for the TP with CLM3.5 and RegCM4, respectively; these experiments are hereafter referred to as the NEW experiment. All model settings are similar to those of the CTRL experiment.

2.5　Statistical analysis of simulation results

The simulated results from the CTRL and NEW experiments were compared with the observed data,on the basis of three key statistical analyses of the correlation coefficient (Corr), bias (Bias), and standard error of the estimate (SEE). The methods of calculating Corr, Bias, and SEE are as follow:whereMiis the simulated result,Oiis the observed value, andnis the total number of data;is the average simulation; andis the average observation.

3　Simulation results and analysis

3.1　Offline simulation

3.1.1Simulation of soil moisture

Figure 1 shows a comparison of observed data, the CTRL result, and the NEW result of liquid water content in soil layers. At the 10-cm soil layer, the liquid water content drop during the freezing period in the CTRL experiment occurred slightly earlier than that observed; and the liquid water content drop during the thawing period occurred approximately 20 d before the observed, followed by several drastic fluctuations when compared with the observed. Compared with the CTRL experiment, the NEW experiment showed no significant improvement; and the freeze-thawing fluctuation declined slightly during late thawing. At the 20-cm layer, the liquid water content drop in the CTRL experiment during different periods occurred 15 d before the observed. No obvious improvement was noted during the freezing period in the NEW experiment, but a significant improvement was noted during the thawing period. The liquid water content drop in the NEW experiment still occurred earlier than the observed. For 40-cm and 80-cm soil layers,the liquid water content drop in the CTRL experiment occurred earlier than the observed; and that in the NEW experiment fitted the observed better.Figure 2 shows the time profile of the observed and simulated soil liquid water content variation with soil depth. During the freezing and thawing periods, the sudden change time of liquid water content was close to the observed. Figure 3 shows the time profile of the simulated soil ice content variation with soil depth. In the CTRL experiment, the maximum simulation depth of ice content was close to 160 cm; and it was only about 100 cm in the NEW experiment. This result indicates that the NEW experiment reduced frozen depth more significantly, compared with the CLM3.5 model simulation. Moreover, the simulated ice content of all soil layers decreased to different extents.

Figure 1　Comparison of the simulated soil liquid water content by CTRL experiment (gray line) and NEW experiment (dotted line)with observations (solid line) at depths of 10 cm (a), 20 cm (b), 40 cm (c), and 80 cm (d) (unit: m3/m3)

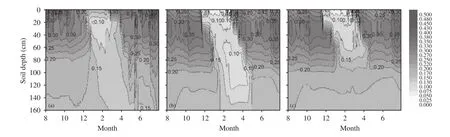
Figure 2　Time-depth cross section of observed soil liquid water content (a), simulation by CTRL experiment (b),and simulation by NEW experiment (c) (unit: m3/m3)

3.1.2Simulation of soil temperature

Figure 4 presents a comparison of observed,CTRL, and NEW temperatures of four soil layers.The difference between the NEW experiment and the CTRL experiment was small in soils less than 40 cm deep and became evident at the 80-cm depth. At the 80-cm soil layer, the CTRL temperature was higher than the observed from August to October but lower during complete freezing. The time for soil temperat-ure to drop to 0 °C during freezing decreased, and the time for soil temperature to rise to 0 °C during thawing was earlier than the observed. The NEW experiment presented some improvement. The simulated soil temperature during complete thawing was lower than that in the CTRL experiment, but the simulated soil temperature during complete freezing was higher.The simulated time of freeze-thawing was also close to the observed. At the 160-cm soil layer, the CTRL temperatures from August to December were slightly higher than the observed but lower the rest of the time. The minimum observed temperature (about 1 °C) occurred in May 2010. The minimum CTRL temperature was close to 0 °C. In the NEW experiment, the soil temperature from August to October and from May to July of the next year was slightly lower than the observed but higher the rest of the time. The minimum soil temperature in the NEW experiment agreed with the observed. Figure 5 shows the time profile of observed and simulated soil temperature variations with soil depth. The deepest 0 °C isotherm at the end of February was about 100 cm, indicating that the maximum freezing soil depth at the Zoige Station was about 100 cm. In the CTRL experiment, the deepest 0 °C isotherm reached 140 cm; and-2 °C and -4 °C isotherms were deeper than the observed. This result demonstrates that during the freezing period, the simulated deep soil temperature was relatively low and the simulated soil frozen depth relatively high. In the NEW experiment, the low point of the 0 °C isotherm was about 110 cm and was closer to the observed, compared with the CTRL experiment.During the unfrozen period, the NEW experiment performed better than the CTRL experiment. For example, the low points of the 12 °C and 14 °C isotherms approached the observed.

Figure 3　Time-depth cross section of the simulated soil ice content by CTRL experiment (a)and NEW experiment (b) (unit: m3/m3)

3.1.3Discussion of offline experimental results

Table 3 shows statistical results of simulated and observed soil moisture and soil temperature. As illustrated in Table 3, the average SEE of soil temperature is reduced from 1.19 °C in the CTL experiment to 1.05 °C in the NEW experiment. Also, more substantial improvements of soil liquid water content occurred where the SEE of all soil layers in the NEW experiment was smaller than that in the CTRL experiment; and the average SEE was reduced from 6.55%in the CTL experiment to 5.90% in the NEW experiment. Owing to the large difference in the thermal properties of ice and water, soil thermal conductivity increases significantly upon freezing. The numerical value of the thermal conductivity of ice is equivalent to the thermal conductivity of mineral soil solid at the Zoige Station, calculated with Johansen's scheme.Therefore, ice content in the frozen soil simulation was vital to the calculation of soil thermal conductivity. The thermal conductivity of mineral soil solid calculated with the CLM3.5 model was significantly high (Table 1). Such a large error was more prominent in calculating the thermal conductivity for deeper soil. Deep soil temperature was relatively high during complete thawing but relatively low during freezing.The relatively low simulated soil temperature led to a relatively high simulated ice content. Owing to the high thermal conductivity of ice, the simulated thermal conductivity error of frozen soil was large,thereby lowering the simulated soil temperature. A positive error feedback was formed, which was the main cause of the larger simulation error of soil temperature during the freezing period than during complete thawing. The high simulated soil thermal conductivity enabled energy to be transferred to deep soil layers, resulting in warmer temperature in summer in the CLM3.5 model simulation than the observed.Similarly, the existence of ice intensified the simulation error of thermal conductivity of frozen soil, resulting in colder temperature in winter and higher frozen depth than the observed. During early thawing,the high thermal conductivity of frozen soil caused a rapid energy transmission rate between soil layers and accelerated onset of the thawing process. This phenomenon was manifested by a higher soil thawing rate and earlier drop in soil liquid water content than the observed. Moreover, soil organic carbon is a very important factor that significantly reduces thermal conductivity on the Tibetan Plateau (Yanget al.,2005; Chenet al., 2012b). The impact of soil organic carbon on the thermal and hydraulic properties of soil is not typically accounted for in land surface models,including the CLM3.5 model (Lawrence and Slater,2008). Accounting for measured data from the Zoige Station indicates that the soil (0-60 cm) contains high soil organic carbon content (Xionget al., 2014). The simulated biases of soil temperature and the early date of freezing-thawing are partly due to the thermal conductivity parameterization scheme's excluding soil organic carbon.

After Johansen's scheme was introduced into CLM3.5, the thermal conductivity of mineral soil solid decreased significantly (decreased to one-third).The simulation errors of soil temperature, frozen depth, and time of sudden changes in liquid water content were reduced to a certain extent. Additionally,the simulated temperature of frozen soil in the NEW experiment remained lower than the observed value.This condition may be related to the simulation error of surface soil heat flux, except for the calculation error of soil thermal conductivity.

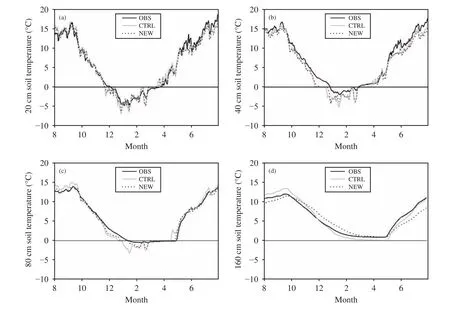
Figure 4　Comparison of the simulated soil temperature by CTRL experiment (gray line) and NEW experiment (dotted line)with observations (solid line) at depths of 20 cm (a), 40 cm (b), 80 cm (c), and 160 cm (d) (unit: °C)

Figure 5　Time-depth cross section of observed soil temperature (a), simulation by CTRL experiment (b),and simulation by NEW experiment (c) (unit: °C)

Table 3　Statistical results of simulated and observed soil moisture and soil temperature for CTRL and NEW experiments

3.2　Regional simulation

3.2.1Comparison of simulated soil temperature at weather stations

The applicability of the RegCM model for the TP has been proven by numerous tests (Lianget al.,2009; Quet al., 2009). The RegCM model can efficiently simulate air temperature and precipitation on the TP, but the air temperature simulation exhibits cold deviation; and simulated precipitation is relatively higher in several regions than the observed.However, only a few studies on the soil temperature simulation effect of the RegCM model have been reported.

Also, there are limited observational data on soil temperature over successive years. In this study, soil temperature data in four relatively high quality stations (Dari, Maduo, Golmud, and Nagchu) were selected. The monthly average data were used as the verification data of the model. The geographic coordinates and elevation of the four testing stations are presented in Table 4. The simulation results of the observation stations (or areas closest to the grid point)were selected for comparison with the observed results. Considering the disagreement between the simulated depth and the observed depth, observed soil temperature was interpolated linearly onto the depth of the simulated results. Three soil depths were involved,namely, surface (about 2 cm), shallow (about 20 cm),and deep (about 172 cm) layers.

Figure 6 shows a comparison of observed, CTRL,and NEW simulated soil temperatures at the four abovementioned stations. The simulated results could capture seasonal changes in different layer soil temperatures, but the simulation effect differed significantly at the different stations. The overall simulation effect at Dari and Maduo (columns a and b) was good but poor at Golmud and Nagchu (columns c and d),which presented a low simulated soil temperature of all layers. Table 5 shows the Bias for the simulation results relative to the observed result in winter (January) and summer (July). The following three points from Figure 6 and Table 5 deserve further discussion.

First, the simulation result of soil temperature differed at the different stations on the TP. The result was poor at several stations. The simulation error of the annual average value could reach as high as 10 °C.Viewed from the terrain, the elevation of the Golmud Station is lower than 3 km, the lowest among the four observation stations. However, the Golmud area has complicated terrain, which is located in the Qaidam Basin, with the Tanggula Mountains crossing this region. Therefore, valleys at more than 2,000 m elevation and mountain peaks at more than 6,000 m elevation exist. Many studies (Gaoet al., 2006; Zhou and Wang, 2007) have reported that the RegCM model has a poor simulation effect in regions with large topographic relief. On the one hand, the model resolution is inadequate to describe the geographical features of these regions. On the other hand, theσsurface slope in steep regions is large and thus increases the physical level derivatives (including the vertical changes in physical parameters) under the terrain coordinate, thereby increasing the calculation error.Zhanget al. (2005) pointed out that the RegCM model performs poorly in simulating air temperature and precipitation in the Golmud region. Viewed from their geographic locations, Dari and Maduo in the eastern regions of the TP present relatively satisfactory simulation; but the Nagchu Station in the middle of the TP provides poor simulation. This condition may be due to the fact that there are inadequate observation data for data reanalysis and assimilation, as only a few observation stations exist in the middle of the TP. A certain error of ERA40 data (the model input data) also exists, thereby causing errors in the generated initial boundary value.

Figure 6　Comparison of the simulated soil temperature by CTRL experiment (blue line) and NEW experiment (red line) with observations (dotted line) at different depths and different stations (a, b, c, and d represent Dari, Maduo, Golmud,and Nagchu, respectively; rows 1, 2, and 3 denote surface, shallow, and deep layers, respectively; unit: °C)

Table 5　The Bias of simulation and observed at different stations; for CTRL experiment and NEW experiment results (unit: °C)

Second, cold bias of soil temperature was observed at all observation stations except for soil layers ≤40 cm at the Dari Station in summer. The simulation error in winter was significantly larger than that in summer. Such cold bias occurs for two reasons.The first reason is that the simulated air temperature of the model on the TP is relatively low. Lianget al.(2009) believed that the RegCM model has 5 °C to 6 °C cold bias on average when simulating the temperature field in TP. Through the earth-atmosphere interaction, low air temperature leads to low soil temperature. Moreover, the soil thermal conductivity calculated in CLM for land surface was relatively high and caused low simulated soil temperature in winter but high simulated soil temperature in summer. This condition can explain why cold bias in winter is more serious than in summer. Soil temperature simulation in summer balances positive and negative errors. On the one hand, low air temperature makes the soil temperature low. On the other hand, high calculated soil thermal conductivity makes the soil temperature high and results in a small error in summer. The second reason is that soil freezing in winter on the TP complicates the soil temperature simulation. The low simulated soil temperature in winter causes high simulated ice content. Hence, the thermal conductivity of frozen soil becomes high and further decreases the simulated soil temperature. This condition forms a positive feedback of deviation and intensifies the cold bias of temperature simulation in winter. At all stations, the annual range of soil temperature in the CTRL experiment was higher than the observed, a finding that also confirms the abovementioned explanation. We can suppose that the model has an ideal atmospheric process and no air temperature simulation error. Then, the simulated soil temperature would be low in winter but high in summer.

Third, the NEW experiment reduced the thermal conductivity of mineral soil solid because of the introduction of Johansen's scheme. Soil thermal conductivity was thus reduced, and the simulated soil temperature differed from that of the CTRL experiment to a certain extent. Such a difference was more obvious in the deep layers. In winter, soil releases energy into the atmosphere. When thermal conductivity is relatively high, energy stored in deep layers could be transmitted to the layers above, thereby lowering the soil temperature in the deep layers. In summer, soil absorbs energy from the atmosphere. When thermal conductivity is relatively high, energy could be transmitted into the deep layers, thereby increasing the soil temperature in those layers. Decreasing soil thermal conductivity can thus reduce the simulation error of soil temperature in the deep layers. Figures 6a3-6d3 show that, in winter, the soil temperature simulated by the NEW experiment was about 2 °C to 3 °C higher than that in the CTRL experiment. At Maduo and Nagchu stations, more substantial improvements occurred where the four layers' average biases were reduced from -2.6 °C and -12.6 °C in the CTL experiment to-1.8 °C and -11.1 °C in the NEW experiment. In summer, the simulated temperature decreased by about 3 °C to 4 °C on the average. Although the difference between the simulated and observed results increased further, such a reduction is reasonable, considering the overall cold bias of soil temperature. Furthermore, the NEW experiment reduced the annual range of soil temperature significantly and conformed to the observation better. The average biases of the soil temperature annual range were reduced from -2.7 °C,1.3 °C, 3.5 °C, and 7.1 °C in the CTL experiment to 0.6 °C, -0.7 °C, 2.4 °C, and 3.4 °C in the NEW experiment at these four stations. The variation in simulated soil temperature was less prominent in winter than in summer. The existence of frozen soil complicated the calculation of soil thermal conductivity. Ice and mineral soil solid have equivalent thermal conductivity. Therefore, reducing the thermal conductivity of mineral soil solid affects frozen soils more significantly than unfrozen soils.

Figure 7 shows the profile map of simulated soil temperature variation at Dari and Maduo with soil depth and time. The model could simulate variation in soil temperature at different depths with time at these two stations. It could reflect the area penetrated by heat in summer and by cold in winter, but a slight deviation was observed in penetrated depth in winter.With the Dari Station (Figure 7a) as an example, the 0 °C isotherm reached the deepest (about 175 cm) in March, indicating that the Dari Station possessed seasonally frozen soils; and the maximum frozen depth was approximately 175 cm. On the CTRL map, the 0 °C isotherm exceeded the 180-cm depth. The simulation frozen depth increased significantly. On the NEW map, the frozen depth was still high; and the 0 °C isotherm exceeded the 180-cm depth; however,the simulation depth of the other negative isotherms decreased. For instance, the bottom of the -2 °C isotherm was approximately 170 cm in the CTRL experiment and approximately 150 cm in the NEW experiment. The low point of the -4 °C isotherm was approximately 130 cm in the CTRL experiment and approximately 120 cm in the NEW experiment. In the observation of Maduo Station, the frozen depth exceeded 180 cm. The frozen depth in the CTRL map was greater than the observed one, and freezing lasted longer. The frozen depth in the NEW map also exceeded the observed value; but the simulation depths of the other negative isotherms decreased to a certain extent, compared with those in the CTRL experiment.After the thermal conductivity of mineral soil solid was reduced, simulation of the cold biases in winter improved to a certain extent; but the frozen depth remained great.

3.2.2Regional simulation of soil temperature

Figures 8 and 9 show the soil temperatures (at 80 and 160 cm) simulated by the CTRL and NEW experiments in January and July, as well as their differences. It is impossible to verify the large-scale simulation because of inadequate observation data.

On the 80-cm map, the simulated soil temperature in January was generally lower than 0 °C, decreasing from east to west and reaching the valley in the northwest. The simulated temperature was -4 °C to 0 °C in western Sichuan and eastern Tibet, -8 °C to -4 °C in most regions of Qinghai and the middle region of Tibet, and -8 °C in northwest Tibet. On the difference map, the NEW experiment simulated a higher soil temperature than the CTRL experiment (2 °C to 3 °C higher) in most regions of TP, except at several marginal areas, especially in the middle of TP. In July, the simulated soil temperature in most regions of the TP except for several areas in northwestern TP was above 0 °C. The temperature was 0 °C to 4 °C in most regions of Tibet, southern Qinghai, and western Sichuan; 4 °C to 8 °C in the middle regions of Tibet;and 8 °C to 12 °C in the Qaidam Basin in northern Qinghai. The NEW experiment reported a significantly lower soil temperature than the CTRL experiment (up to 3 °C to 4 °C), especially in the middle and western regions of TP.

Figure 7　Time-depth cross section of the observed soil temperature, (a1) and (b1); simulation by CTRL experiment (a2) and (b2);and simulation by NEW experiment (a3) and (b3); at Dari Station (row 1) and Maduo Station (row 2) (unit: °C)

Figure 8　The simulated soil temperature by CTRL experiment, (a) and (b); NEW experiment, (c) and (d); and their differences, (e) and (f), in January and July at the depth of 80 cm (unit: °C)

Figure 9　The simulated soil temperature by CTRL experiment, (a) and (b); NEW experiment, (c) and (d); and their differences, (e) and (f), in January and July at the depth of 160 cm (unit: °C)

On the 160-cm map, the simulated soil temperature in January was generally still lower than 0 °C but slightly higher than that at the 80-cm soil layer. Most regions in the TP had a temperature of -4 °C to 0 °C,and the low temperature area (-8 °C) narrowed significantly. This condition occurred only in the Kunlun Mountains. The NEW experiment obtained a significantly higher soil temperature than the CTRL experiment, especially in the middle of the TP. The soil temperature simulated in the NEW experiment was 1 °C to 4 °C higher in the middle and western regions of Tibet and most regions of Qinghai. The simulated soil temperature in July was lower than that at the 80-cm soil layer, and several places had temperature higher than 0 °C. The soil temperature simulated by the NEW experiment was lower than that by the CTRL experiment in most regions of the TP.

In the NEW experiment, the simulated soil temperature changed to a certain extent in deep layers in most regions of the TP. Soil temperature increased in winter but decreased in summer. Considering the overall low air temperature simulated by the RegCM model, Johansen's scheme was applied to replace the thermal conductivity parameterization in the CLM3.5 model, which decreases the simulation error of soil temperature in winter but may increase the simulation error in summer. The soil temperature simulated by RegCM-CLM has a certain reference value for the estimation of frozen soil area and frozen depth. To improve calculation accuracy, atmospheric process parameterization must be perfected; and the cold bias of air temperature must be eliminated. Frozen soil parameterization during the land surface process may require further improvement.

4　Conclusions

Soil thermal conductivity is one of the key thermal properties of numerical models used in the determination of soil temperature and heat flux. To overcome the high thermal conductivity parameters of mineral soil solid in the TP as calculated with CLM3.5, Johansen's scheme was applied to replace the parameterization in CLM3.5. The improved CLM3.5 and RegCM4-CLM3.5 were utilized to conduct offline and regional simulation experiments in the TP. Comparison of the new and old schemes yielded the following conclusions.

(1) CLM3.5 provides high thermal conductivity parameters of mineral soil solid in the TP, thereby causing certain simulation errors in offline experiments. For example, the simulated temperature was warmer in summer and colder in winter than the observed; and the sudden change in liquid water content during freezing and thawing periods was earlier than the observed. The high thermal conductivity of ice increased the simulation error of soil thermal conductivity during thawing. The low temperature increased the simulated ice content and further increased the thermal conductivity of frozen soils. Such positive feedback caused poorer simulation of frozen soil than of unfrozen soil.

(2) Johansen's scheme is more practical for the TP than the soil thermal conductivity parameterization in CLM3.5. Here, Johansen's scheme was used to replace the parameterization of CLM3.5 to conduct an offline simulation experiment at the Zoige Station; it achieved a better simulation effect than CLM3.5. The sudden change time of liquid water content was closer to the observed. The simulation of soil temperature during freezing improved to a certain extent.

(3) Johansen's scheme was introduced into the RegCM4-CLM3.5 model to conduct a simulation experiment on the entire TP. Significant changes were noted in soil temperature simulation deeper than 80 cm. Soil temperature increased in winter but decreased in summer. The cold bias in winter and soil temperature has been decreased. The annual range of soil temperature decreased significantly. Considering the overall cold bias of temperature simulation, the improved parameterization could reduce the simulation error of soil temperature in winter but may increase the simulation error in summer.

This work is supported by the National Natural Science Foundation of China (91537104, 41375077,41775016, 41405015, and 41405016). The authors also acknowledge all the participants for their very hard fieldwork during the observations at the Zoige Plateau Wetlands Ecosystem Research Station and the support for using the computing resources at the Supercomputing Center of Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences.

Avissar R, Pielke RA, 1989. A parameterization of heterogeneous land surfaces for atmospheric numerical models and its impact on regional meteorology. Monthly Weather Review, 117(10):2113-2136. DOI: 10.1175/1520-0493(1989)117.

Bhattacharya A, Mandal M, 2015. Evaluation of Noah land-surface models in predicting soil temperature and moisture at two tropical sites in India. Meteorological Applications, 22(3): 505-512. DOI:10.1002/met.1481.

Chen BL, Lü SH, Luo SQ, 2012a. Simulation analysis on land surface process at Maqu station in the Qinghai-Xizang Plateau using community land model. Plateau Meteorology, 31(6): 1511-1522.

Chen BL, Luo SQ, Lü SH,et al., 2014a. Validation and comparison of the simulation at Zoigê Station during freezing and thawing with land surface model CLM. Climatic and Environmental Research,19(5): 649-658. DOI: 10.3878/j.issn.1006-9585.2014.13013.

Chen BL, Luo SQ, Lü SH,et al., 2014b. Effects of the soil freeze-thaw process on the regional climate of the Qinghai-Tibet Plateau. Climate Research, 59(3): 243-257. DOI: 10.3354/cr01217.

Chen YY, Yang K, Tang WJ,et al., 2012b. Parameterizing soil organic carbon's impacts on soil porosity and thermal parameters for Eastern Tibet grasslands. Science China Earth Sciences, 55(6):1001-1011. DOI: 10.1007/s11430-012-4433-0.

Côté J, Konrad JM, 2005a. Thermal conductivity of base-course materials. Canadian Geotechnical Journal, 42(1): 61-78. DOI:10.1139/t04-081.

Côté J, Konrad JM, 2005b. A generalized thermal conductivity model for soils and construction materials. Canadian Geotechnical Journal, 42(2): 443-458. DOI: 10.1139/t04-106.

Elguindi N, Bi XQ, Giorgi F,et al., 2011. Regional climatic model RegCM user manual version 4.1. Trieste, Italy: International Centre for Theoretical Physics.

Fang XW, Luo SQ, Lyu SH,et al., 2016. A simulation and validation of CLM during freeze-thaw on the Tibetan Plateau. Advances in Meteorology, 2016: 9476098. DOI: 10.1155/2016/9476098.

Farouki OT, 1981. The thermal properties of soils in cold regions. Cold Regions Science and Technology, 5(1): 67-75. DOI:10.1016/0165-232X(81)90041-0.

Farouki OT, 1986. Thermal Properties of Soils. Clausthal-Zellerteld:Trans Tech Publication, pp. 12-28.

Findell KL, Pitman AJ, England MH,et al., 2009. Regional and global impacts of land cover change and sea surface temperature anomalies. Journal of Climate, 22(12): 3248-3269. DOI:10.1175/2008JCLI2580.1.

Gao XJ, Xu Y, Zhao ZC,et al., 2006. Impacts of horizontal resolution and topography on the numerical simulation of East Asian precipitation. Chinese Journal of Atmospheric Sciences, 30(2): 185-192.DOI: 10.3878/j.issn.1006-9895.2006.02.01.

Gao ZQ, 2005. Determination of soil heat flux in a tibetan short-grass prairie. Boundary-Layer Meteorology, 114(1): 165-178. DOI:10.1007/s10546-004-8661-5.

Gao ZQ, Fan XG, Bian LG, 2003. An analytical solution to one-dimensional thermal conduction-convection in soil. Soil Science,168(2): 99-107. DOI: 10.1097/00010694-200302000-00004.

Giorgi F, Elguindi N, 2011. Regional climatic model RegCM User's guide version 4.2. Trieste, Italy: International Centre for Theoretical Physics.

Johansen O, 1975. Thermal Conductivity of Soils. Trondheim, Norway: University of Trondheim, pp. 236.

Koren V, Schaake J, Mitchell K,et al., 1999. A parameterization of snowpack and frozen ground intended for NCEP weather and climate models. Journal of Geophysical Research: Atmospheres,104(D16): 19569-19585. DOI: 10.1029/1999JD900232.

Lawrence DM, Slater AG, 2008. Incorporating organic soil into a global climate model. Climate Dynamics, 30(2-3): 145-160. DOI:10.1007/s00382-007-0278-1.

Lawrence PJ, Chase TN, 2007. Representing a new MODIS consistent land surface in the Community Land Model (CLM 3.0). Journal of Geophysical Research: Biogeosciences, 112(G1): G01023. DOI:10.1029/2006JG000168.

Liang L, Li YQ, Hu HR,et al., 2009. Simulation of air temperature and precipitation over Qinghai-Xizang Plateau with RegCM3 model.Scientia Meteorologica Sinica, 29(5): 611-617. DOI:10.3969/j.issn.1009-0827.2009.05.007.

Liu XD, Chen BD, 2000. Climatic warming in the Tibetan Plateau during recent decades. International Journal of Climatology, 20(14):1729-1742. DOI: 10.1002/1097-0088(20001130)20:14.

Lu S, Ren TS, Gong YS,et al., 2007. An improved model for predicting soil thermal conductivity from water content at room temperature. Soil Science Society of America Journal, 71(1): 8-14. DOI:10.2136/sssaj2006.0041.

Luo SQ, Lü SH, Zhang Y, 2009a. Development and validation of the frozen soil parameterization scheme in Common Land Model. Cold Regions Science and Technology, 55(1): 130-140. DOI:10.1016/j.coldregions.2008.07.009.

Luo SQ, Lü SH, Zhang Y,et al., 2008. Simulation analysis on land surface process of BJ site of central Tibetan Plateau using CoLM.Plateau Meteorology, 27(2): 259-271.

Luo SQ, Lü SH, Zhang Y,et al., 2009b. Soil thermal conductivity parameterization establishment and application in numerical model of central Tibetan Plateau. Chinese Journal of Geophysics, 52(4):919-928. DOI: 10.3969/j.issn.0001-5733.2009.04.008.

Manabe S, Broccoli AJ, 1990. Mountains and arid climates of middle latitudes. Science, 247(4939): 192-195. DOI: 10.1126/science.247.4939.192.

Niu GY, Yang ZL, 2006. Effects of frozen soil on snowmelt runoff and soil water storage at a continental scale. Journal of Hydrometeorology, 7(5): 937-952. DOI: 10.1175/JHM538.1.

Niu GY, Yang ZL, Dickinson RE,et al., 2005. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models. Journal of Geophysical Research: Atmospheres,110(D21). DOI: 10.1029/2005JD006111.

Niu GY, Yang ZL, Dickinson RE,et al., 2007. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data. Journal of Geophysical Research: Atmospheres, 112(D7). DOI:10.1029/2006JD007522.

Oleson KW, Dai YJ, Bonan G,et al., 2004. Technical description of the Community Land Model (CLM). NCAR Technical Note NCAR/TN-461+STR. DOI: 10.5065/D6N877R0.

Overduin PP, Kane DL, van Loon WKP, 2006. Measuring thermal conductivity in freezing and thawing soil using the soil temperature response to heating. Cold Regions Science and Technology,45(1): 8-22. DOI: 10.1016/j.coldregions.2005.12.003.

Peter-Lidard CD, Blackburn E, Liang X,et al., 1998. The effect of soil thermal conductivity parameterization on surface energy fluxes and temperatures. Journal of the Atmospheric Sciences, 55(7):1209-1224. DOI: 10.1175/1520-0469(1998)055.

Qu P, Yang MX, Guo DL,et al., 2009. Simulation of summer air temperature and precipitation over Tibetan Plateau with regional climate model (RegCM3). Plateau Meteorology, 28(4): 738-744.

Sun SF, 2005. Physical, Biochemical Mechanism and Parametric Model of Land Surface Processes. Beijing: Meteorological Press, pp.84.

Thornton PE, Zimmermann NE, 2007. An improved canopy integration scheme for a land surface model with prognostic canopy structure. Journal of Climate, 20(15): 3902-3923. DOI:10.1175/JCLI4222.1.

Vertenstein M, Oleson KW, Levis S,et al., 2004. Community land model version 3.0 (CLM3.0) user's guide. Boulder, CO: National Center for Atmospheric Research.

Xiong JS, Zhang Y, Wang SY,et al., 2014. Influence of soil moisture transmission scheme improvement in CLM4.0 on simulation of land surface process in Qinghai-Xizang Plateau. Plateau Meteorology, 33(2): 323-336. DOI: 10.7522/j.issn.1000-0534.2014.00012.

Yang K, Koike T, Ye BS,et al., 2005. Inverse analysis of the role of soil vertical heterogeneity in controlling surface soil state and energy partition. Journal of Geophysical Research: Atmospheres,110(D8). DOI: 10.1029/2004JD005500.

Ye DZ, Gao YX, 1979. Meteorology of the Qinghai-Xizang (Tibet)Plateau. Beijing: Science Press.

Yoshikawa K, Bolton WR, Romanovsky VE,et al., 2002. Impacts of wildfire on the permafrost in the boreal forests of Interior Alaska.Journal of Geophysical Research: Atmospheres, 107(D1). DOI:10.1029/2001jd000438.

Zhang DF, Gao XJ, Bai HZ,et al., 2005. Simulation of climate over Qinghai-Xizang Plateau utilizing RegCM3. Plateau Meteorology,24(5): 714-720. DOI: 10.3321/j.issn:1000-0534.2005.05.009.

Zhou JW, Wang YQ, 2007. The advance in application and research of regional climate model RegCM3. Scientia Meteorologica Sinica,27(6): 702-708. DOI: 10.3969/j.issn.1009-0827.2007.06.018.