节点相似度辅助下的线要素匹配方法设计

方　敏，霍　亮，宋　磊，鲍　鹏，王　锐，田　军

(1. 北京建筑大学测绘与城市空间信息学院，北京 100044； 2. 现代城市测绘国家测绘地理信息局重点实验室，北京 100044； 3. 北京城建勘测设计研究院有限责任公司，北京 100101)

同名要素匹配是空间数据集成、更新和融合的关键技术，线要素是矢量空间数据的常见类型，其匹配也是当前空间数据匹配领域研究的焦点之一[1]。目前，线要素匹配采用的方法有缓冲区分析法[2-3]、几何距离法(Hausdorff、Fréchet距离)[4-5]、结构拓扑法[6-7]等，在得到匹配候选指标后，可以进一步采用概率松弛法[8]和模糊信息处理理论[9]寻找最优匹配，采用稳健估计[10]等方法剔除错误匹配，得到最终的匹配结果。

现有的线要素匹配文献主要是针对GPS轨迹[11]或城市简单路网[3]，而对一些拓扑结构较为复杂的线要素研究较少，诸如水系网和复杂道路网的匹配，这些线要素在匹配时必须考虑要素的连续性和拓扑一致性等特征。本文设计了一种基于节点相似度，顾及拓扑、方向、距离等多方面特征的线要素匹配方法，在保证拓扑一致性的前提下，为线要素匹配提供了切实可行的技术方案。

1　线要素匹配模型设计

要素匹配主要是根据不同数据源中对同名实体的识别和数据交换，根据要素的数据特点对同名实体之间的相似性进行判断，以此来确定是否相互匹配[12]。考虑空间数据在尺度及空间变换上于平移、旋转、缩放和数据综合方面存在的任意性，根据线要素的几何特征和图论拓扑连通关系，确定要选取的度量指标，以节点、方向、距离3个因子作为匹配指标，其中节点处包含的点集为主要匹配对象，其对应的节点相似度为匹配的主要前提。

本文设计的线要素匹配模型，定义了3种类型的空间关系约束，分别为：拓扑约束(节点相似度)、方向约束(方向相似度)、距离约束(位置相似度)。首先利用节点的度来进行粗匹配；然后在满足方向和距离约束的前提下，对候选匹配集中每个实体的方向和位置两个匹配约束参数进行归一化处理，并加权计算总的空间相似值；最后选取空间相似值最大的点集作为最终的同名节点。

1.1　节点相似度

节点的度是源于复杂网络的一个概念，在网络中，节点的度就是这个节点与其他节点相连接边的数量[13]。相似度测量的是一对节点之间的亲密程度，从结构上看，如果两个节点的连接情况很相似，那么这两个节点可能是一对同名点。

在匹配的过程中，以节点相似度为判断的先决条件，如果节点的度一致，则加入候选匹配点集中，若节点的度不一致，则予以排除。即对于给定的目标数据集中一个节点Pi，首先给定一个缓冲区半径R，然后在参考数据集中寻找缓冲区范围之内的节点，依次记为Mi1，Mi2，…，Min，它们构成候选匹配点集，记为Qi。本文定义的节点相似度约束为

TPNode(Pi)=TPNode(Mij)=n

(1)

式中，n表示节点的连通度。

1.2　方向相似度

空间要素间的方向差异性常用空间要素方向的夹角表示[14]。在复杂的网络中，线要素是互相连通的，方向用来判断线要素的走向，可以作为相似性度量的一个重要因子。本文通过计算线要素节点的顺时针夹角来进行方向的度量，即以正北方向为零指向，按顺时针方向依次递增，每个节点按连接弧段之间的夹角取值范围为[0，180°]，如图1所示。

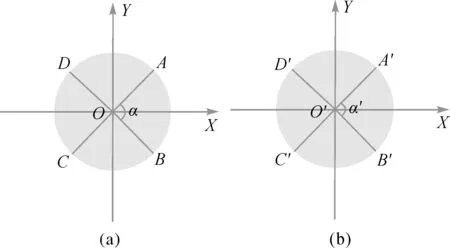
图1　夹角示意图

图1(a)、(b)分别为待匹配数据和参考数据，以O、O′为中心节点，落在圆周上的其余点均为与中心节点相连接的节点。计算弧段夹角时，需要设定好中心节点，找到与中心节点相连的一个端点作为计算的起始点，也是夹角计算方向的起点，以图(a)为例，设置好中心节点O，与之相连的节点分别为A、B、C、D，从起始弧段(OA边)顺时针开始，依次计算与O关联的4个弧段夹角。每个夹角采用余弦定理进行计算，相应的节点连接弧段方向约束定义为

(2)

式中，k表示第k个相应的连接弧段；Δ∂表示连接弧段之间的方向差异阈值。

每个节点与之相连的节点个数为n(n>2)，则该节点与其他节点构成的夹角个数为n，依次计算待匹配数据和参考数据节点的各个夹角，通过判断对应夹角差值和角度阈值的大小关系来度量二者的方向相似性。

1.3　位置相似度

位置是空间要素十分重要的特征，同名实体的位置差异在空间表达上表现为在空间位置上不能完全重合，基于这种思想，可以认为同名实体在空间距离上应该是非常接近的。线状实体的相似可以采用距离特征来度量，主要是用来描述实体之间的位置关系，本文采用欧氏距离来进行距离的度量，节点之间的距离约束需满足

(3)

式中，Δd表示两节点之间的位置差异阈值。

基于图1，在进行距离相似性度量时，从中心节点开始，以起始路段顺时针方向计算与中心点相连的路段长度，每个节点与之相连的节点个数为n(n>2)，则该节点与其他节点构成的路段数量为n，依次计算待匹配数据和参考数据节点连接的路段长度，通过判断对应路段距离差值和距离阈值的大小关系来度量二者的位置相似性。

1.4　空间相似值计算

本文根据线要素节点和弧段之间的拓扑关系，建立了待匹配数据节点集合S和参考数据节点集合R之间的多个度量指标约束的匹配判定标准。由几种空间特征加权得到总的空间相似值V，计算公式为

(4)

(5)

式中，λa、λd分别表示方向夹角和距离因子两个指标所占的权重；Va表示两个线状实体集合中所有节点的角度差值总和；Vd表示两个线状实体集合中所有节点弧段的距离差值总和；i为节点编号(i=0,1，…，n)。

空间相似值V经过归一化处理之后，返回值区间为[0，1]。值越大，表明数据越相似，则互为同名要素的可能性越高。

2　线要素匹配流程设计

2.1　匹配算法流程

基于节点相似度的线要素匹配算法，以上述线要素匹配模型为基础，设计了包括数据预处理、候选匹配集获取、3种空间关系约束、空间相似值计算、相似性判断等内容的线要素匹配流程，匹配算法流程如图2所示。

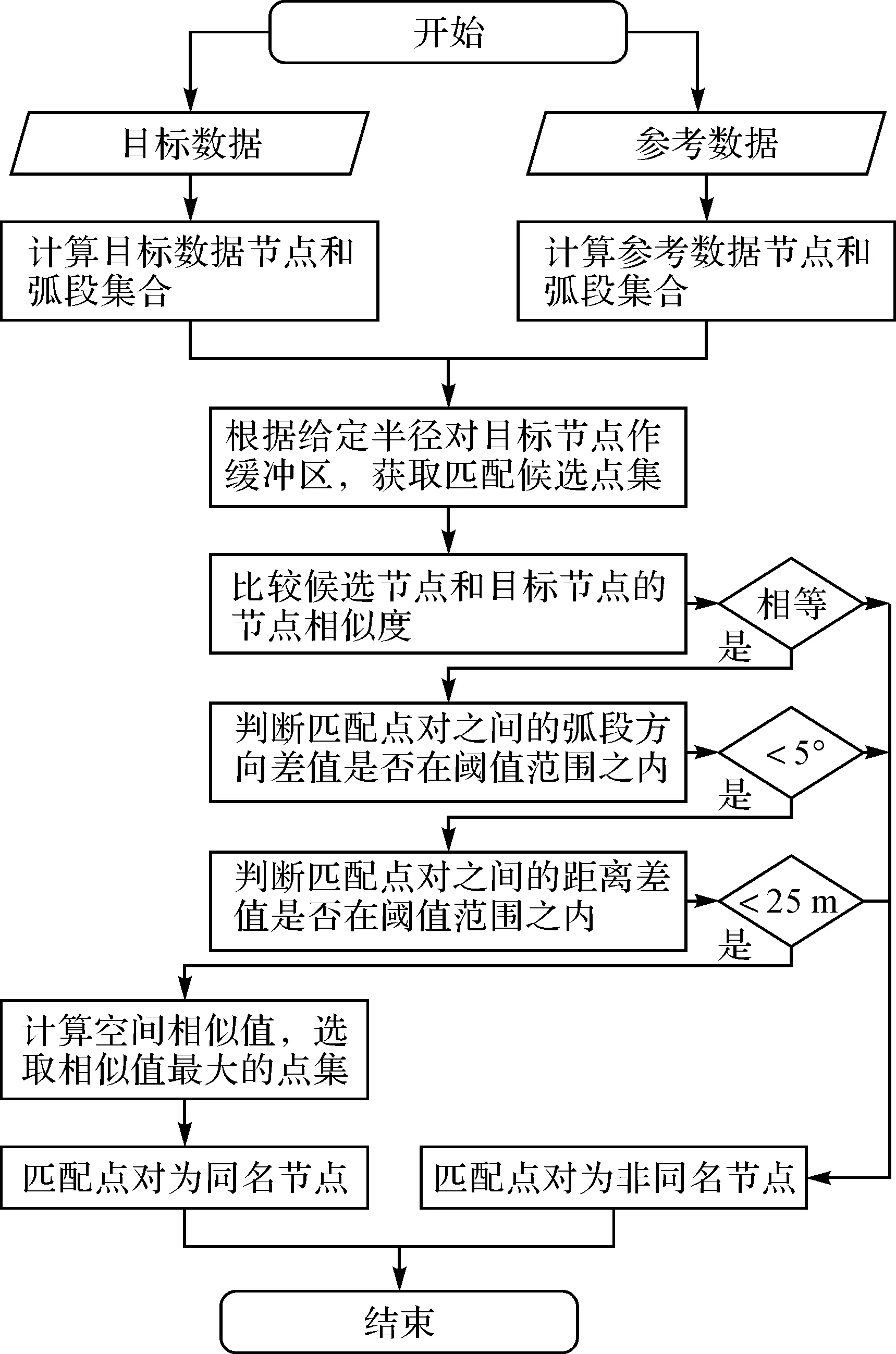
图2　匹配算法流程

2.2　匹配过程描述

由上述算法，可实现线要素的特征点匹配，具体匹配过程可以描述为：

(1) 对参与匹配的目标数据和参考数据进行预处理，计算各自的节点和弧段集合。

(2) 对于给定半径R，通过对目标数据节点设置缓冲区，获取到匹配候选点集Qi1。

(3) 进行拓扑连通性分析，比较候选节点和目标节点的节点相似度：若相等，则加入候选点集合进入下一次判断；反之进行剔除。由此得到候选匹配点集Qi2。

(4) 进行方向相似性判断，比较匹配点对之间的弧段方向差值是否在阈值范围内：若满足阈值范围，加入候选点集合进入下一次判断；反之进行剔除。由此得到候选匹配点集Qi3。

(5) 进行位置相似性判断，比较匹配点对之间的距离差值是否在阈值范围内：若满足阈值范围，加入候选点集合；反之进行剔除。由此得到候选匹配点集Qi4。

(6) 计算总的空间相似值，在得到的Qi4点集中，通过计算加权之后的空间相似值V，选取相似值最大的点集作为最终的同名节点。

3　应用与实例

为了验证本文匹配方法的有效性，以道路网为例，两种数据源分别取自不同时期和不同部门生产的数据。选取某市天地图数据和1∶25万道路网数据进行验证，以1∶25万道路网数据作为待匹配数据，天地图数据为参考数据，试验数据如图3所示。

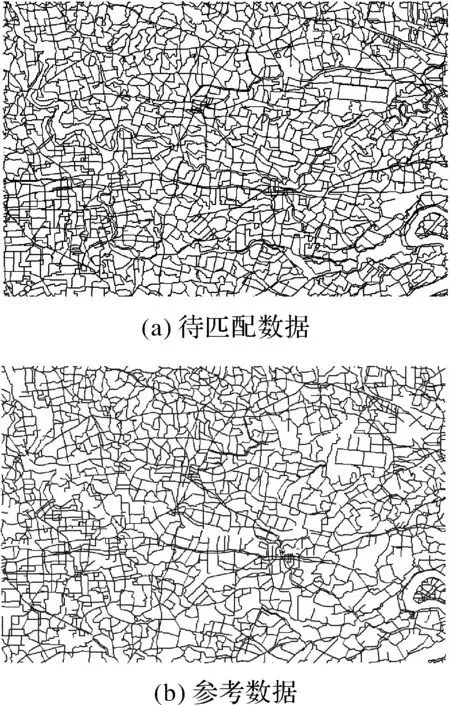
图3　试验数据

3.1　数据预处理

数据结构的一致性是匹配的前提和基础，不同来源的空间数据之间除了同名要素本身内容表达存在不一致的情况之外，二者在坐标系统、地图投影、拓扑结构等方面均存在较大差异。如果要实现多源矢量数据的匹配，必须消除二者之间存在的差异，以保证数据结构的一致性。首先对匹配数据集进行统一的格式转换、拓扑检查和属性检查等处理，消除道路网数据之间的系统误差，以保证拓扑结构的正确性，从而实现原始数据的正确关联；然后提取道路网的特征点作为匹配的研究对象，以点线结构存储的道路网，其特征点主要分为端点、节点、中点等类型，本文选取的匹配特征点主要是节点和端点。由于道路网本身的复杂性，其节点类型也是多种多样的，主要有表1中几种情况。

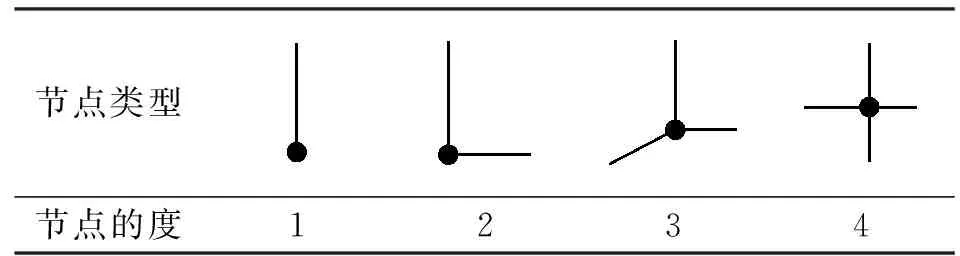
表1　道路网节点类型

在选取的道路特征点中，需要剔除度为2的伪节点，保证节点均出现在度大于2的交叉口处，道路网数据预处理前后对比如图4所示。

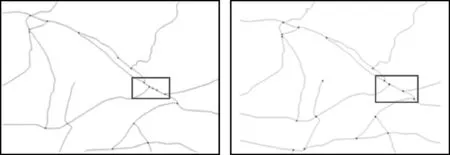
图4　数据对比

3.2　匹配应用与分析

两套道路网数据经过预处理之后，生成了目标路段6631条，参考路段4779条，两套路网数据叠加效果如图5所示。从中可以看出，数据在整体上差异较大，且多呈现出非线性偏差，但局部地区能够较好地吻合。

利用本文算法进行道路网数据匹配时，考虑数据本身的尺度和精度因素，设置缓冲区半径为500 m，方向角度差阈值为5°，距离差阈值为25 m，夹角因子权重0.8，距离因子权重0.2。匹配后部分同名点放大图如图6所示，对匹配后的结果进行统计分析，路网匹配正确率为93%，算法能识别出大部分的同名道路实体，主要是路段1∶1的匹配，由于受数据采集、区域等因素的影响，部分路网数据不能得到正确的匹配，且匹配结果呈现出多种复杂关系，如n∶1、1∶n和m∶n的匹配关系。针对这些未能正确匹配的路段，通过对参考数据集中的路段建立一定的距离阈值的缓冲区[15]，根据缓冲区与待匹配数据集中的路段的位置关系确定候选匹配路段，最后结合相似性度量指标确定候选匹配路段是否与参考路段匹配。对于一些局部地区存在较大差异的路网数据，在实际应用过程中，采用了人工辅助选点，保证了同名点的整体均匀分布。本文设计的线要素匹配算法已经成功应用于大规模道路网数据匹配中，极大地提高了数据生产效率。

图5　数据叠加

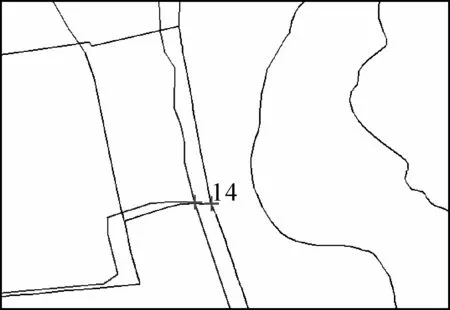
图6　同名点匹配结果放大图

4　结　语

本文针对多源矢量数据匹配问题，通过计算道路节点相似度，结合方向、距离指标的相似度量来确定线要素的匹配关系。通过试验验证，得出以下结论：①顾及拓扑关系和空间位置的多特征度量使得每个相似性特征具有较强的特征差异描述能力，多特征结合可以实现差异互补，整体具有更强的识别能力[16]；②该方法顾及了线要素的连续性和拓扑结构一致性，计算简单，具有一定的实用性。

但本文算法还存在不足之处：①相似性特征之间的权值和阈值设定均是依赖于经验值，自适应能力较差；②文中的试验是针对矢量道路网数据进行的，诸如水系网等不同类型的线要素数据匹配没有经过算法的验证。这些问题将是下一步研究的方向。

参考文献：

[1] 陈竞男，钱海忠，王骁,等.提高线要素匹配率的动态化简方法[J].测绘学报，2016，45(4):486-493.

[2] 胡云岗，陈军，赵仁亮,等.地图数据缩编更新中道路数据匹配方法[J].武汉大学学报(信息科学版)，2010，35(4):451-456.

[3] ZHANG Meng，MENG Liqiu.Delimited Stroke Oriented Algorithm-Working Principle and Implementation for the Matching of Road Networks[J].Geographic Information Sciences，2008，14(1):44-53.

[4] 陈玉敏，龚健雅，史文中.多尺度道路网的距离匹配算法研究[J].测绘学报，2007，36(1):84-90.

[5] DEVOGELE T.Matching Networks with Different Levels of Detail[J].Geoinformation,2008,12(4)：435-453.

[6] 应申，李霖，刘万增,等.版本数据库中基于目标匹配的变化信息提取与数据更新[J].武汉大学学报(信息科学版)，2009，34(6):752-755.

[7] 邓敏，徐凯，赵彬彬,等.基于结构化空间关系信息的结点层次匹配方法[J].武汉大学学报(信息科学版)，2010，35(8):913-916.

[8] 赵东保，盛业华.全局寻优的矢量道路网自动匹配方法研究[J].测绘学报，2010，39(4):416-421.

[9] 宗琴，邓鑫洁，姜树辉.模糊信息处理的道路网匹配方法[J].测绘科学，2016，41(3):167-170.

[10]栾学晨，杨必胜，李秋萍.基于结构模式的道路网节点匹配方法[J].测绘学报，2013，42(4):608-614.

[11]訾宪娟.基于浮动车轨迹数据的路网重构和地图匹配[D].济南：山东大学，2016.

[12]王鹏，郑贵省，王元.基于多相似度量指标的路网匹配算法研究[J].微型机与应用，2016，35(1):19-22.

[13]王艳红.基于节点相似度的复杂网络社区发现算法的研究[D].西安：西安电子科技大学，2014.

[14]翟仁健.基于全局一致性评价的多尺度矢量空间数据匹配方法研究[D].郑州：解放军信息工程大学，2011.

[15]WALTER V，FRITSCH D.Matching Spatial Data Sets：A Statistical Approach[J].International Journal of Geographical Information Science，1999，13(5):445-473.

[16]付仲良，杨元维，高贤君,等.道路网多特征匹配优化算法[J].测绘学报，2016，45(5):608-615.