BDS/GPS/GLONASS RTK定位算法研究
2018-04-08王艺希秘金钟徐彦田
王艺希,秘金钟,徐彦田,王 铎
(1. 辽宁工程技术大学,辽宁 阜新 123000; 2. 中国测绘科学研究院,北京 100830)
目前,随着BDS正式向亚太地区提供服务,以及GLONASS恢复全球组网运行,BDS、GPS与GLONASS三大卫星导航系统形成了并存与竞相发展的局面。多系统组合将显著增加可视卫星数目、改善卫星几何分布构型,进而提高导航定位的可用性、连续性和精度,已成为GNSS导航定位发展的重要趋势[1]。卡尔曼滤波理论作为一种重要的最优估计理论被广泛应用于各种动态数据处理中[2],与单历元解算相比,估算参数的浮点解精度更高。但是在滤波过程中,如果函数模型和滤波参数不准确,会影响滤波的精度和收敛速度[3]。高星伟、唐卫明、施闯、李金龙等研究学者在多系统、多频RTK算法上进行了深入研究,并获取了大量的研究成果[4-7]。本文基于附带参数的卡尔曼滤波算法对多系统RTK算法进行兼容,并对7种不同定位方式进行算例分析。
1 BDS/GPS/GLONASS三系统时空基准统一
时间的统一无非就是寻求一中间变量,并将各自的时间系统都转化到含有相同中间变量的关系式中。BDS、GPS、GLONASS三者的时空基准不同,BDS采用的是BDT,GPS采用的是GPST,GLONASS采用的是GLONASST。其中,BDT、GPST和GLONASST分别以协调世界时UTC(NTSC)、UTC(USNO)和UTC(SU)为基准进行维持,它们之间的关系可表示为
(1)
本文将时间统一到GPST中,使得时间基准得到统一。
虽然BDS采用了CGCS2000坐标系,GPS采用了WGS-84坐标系,但是这两个坐标系统的坐标原点、定向一致,由两个坐标系的参考椭球的扁率差异引起同一点在CGCS2000坐标系和WGS-84坐标系内的坐标变化,对于短基线的影响,在本次试验忽略不计,近似认为属于同一参考框架。BDS采用CGCS2000坐标系,GPS采用WGS-84坐标系,GLONASS采用PZ-90坐标系,笔者参照文献[4]中的方法实现统一到WGS-84坐标系中,在此不再赘述。
2 BDS/GPS/GLONASS RTK定位数学模型
对于短基线RTK而言,双差观测方程可进一步消除接收机钟差和接收机硬件延迟误差,并削弱电离层和对流层延迟,同时保留了双差整周模糊度整数特性[5]。
BDS/GPS伪距和相位的双差观测方程为
(2)
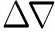
GLONASS伪距和相位的双差观测方程为
(3)
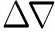
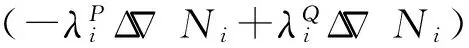
这时可以将观测方程作简单的数学变换,变换后的双差观测方程为
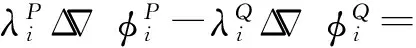
(4)
通过变换后,变成了一个具有整周特性的双差模糊度和一个与参考卫星的单差模糊度有关的两部分。前者的处理与BDS、GPS的双差整周模糊度的处理是一样的,作为未知数来结算;而对后者的处理,可用P码数据或浮点解结果计算一个比较精确的初值,然后将公式中的后一项归入常数项,接下去的处理同BDS/GPS,只是这时得到的浮点解是正确的,而固定解中含有由于单差模糊度的不准确性所带来的微小偏差。但这个偏差对解算整周模糊度来说是可以忽略的。
将三系统同一历元的观测方程联合求解,简化后的BDS/GPS/GLONASS载波相位相对定位的观测方程矩阵式为
(5)
(6)
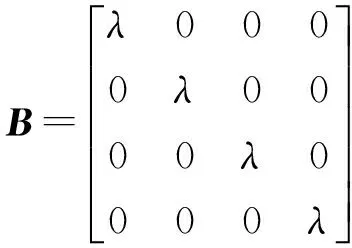
(7)
(8)
3 附有模糊度参数的卡尔曼滤波模型
“滤波”是指通过对所观测到的或接收到的带有干扰的信号剔除干扰信号,取出有用信号的方法。卡尔曼滤波模型包含观测方程和状态方程,通过建立线性离散的状态方程和观测方程,即可进行卡尔曼递推估计[7]。卡尔曼滤波的基本计算过程归结3步:预测、滤波增益、滤波计算更新。其标准卡尔曼滤波递推过程为
(9)
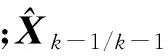
RTK定位中附有模糊度参数的卡尔曼滤波模型中离散化模型中状态向量为
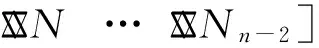
(10)
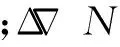
4 BDS/GPS/GLONASS实测数据算例分析
试验分别对BDS、GPS、GLONASS、BDS/GPS、BDS/GLONASS、GPS/GLONASS、BDS/GPS/GLONASS 7种组合方式的实测数据进行处理,采用Trimble R10三系统接收机在河北省石家庄市采集的28 m超短基线及31 km短基线数据,观测时间为2016-12-07,采样间隔率为1 s。
图1表示28 m超短基线东、北、高3方向上的坐标误差值,表1为28 m超短基线初始化时间及RMS值。
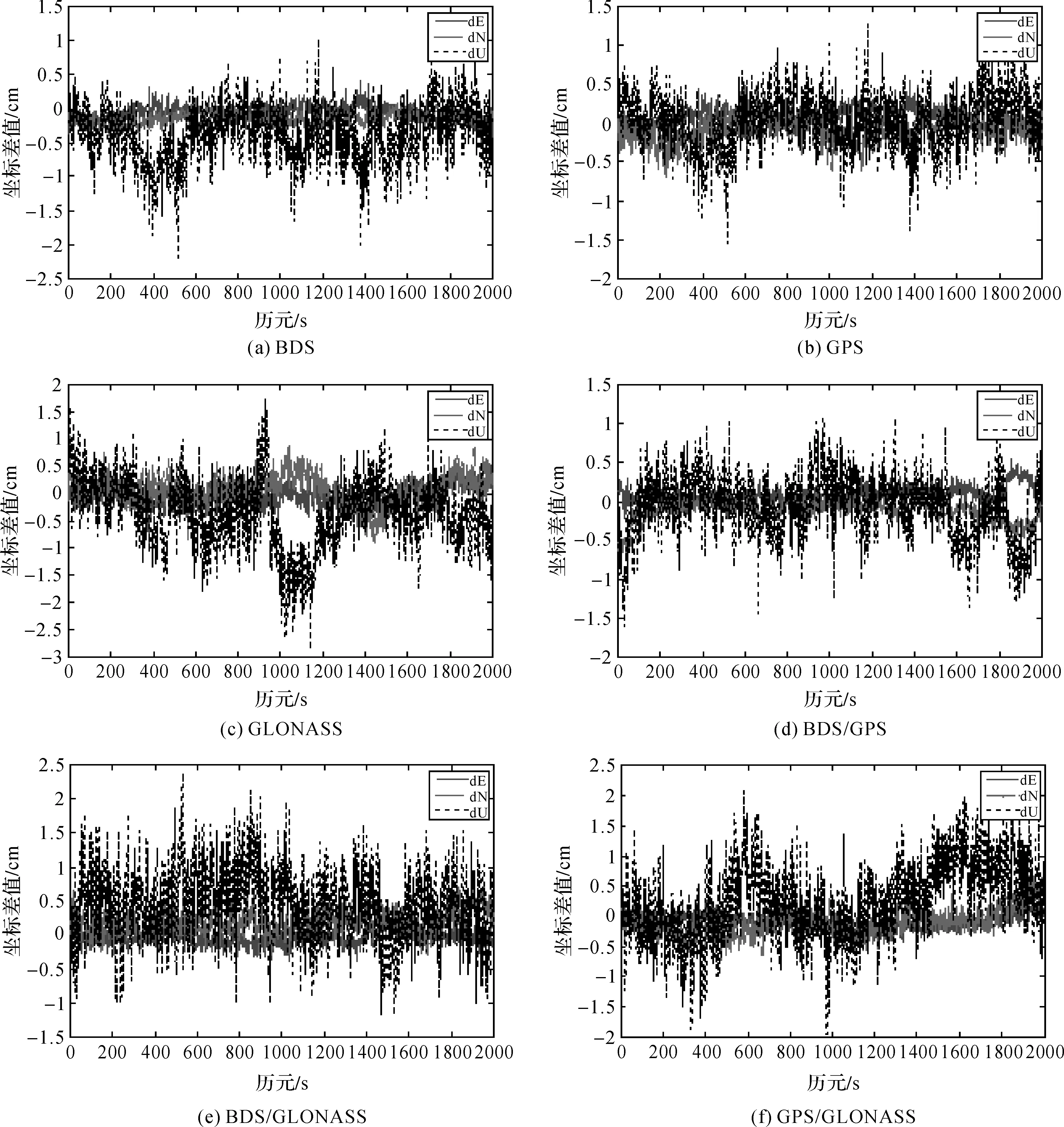
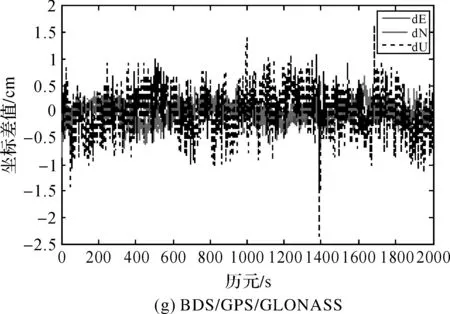
图1 28 m超短基线东、北、高方向坐标差值
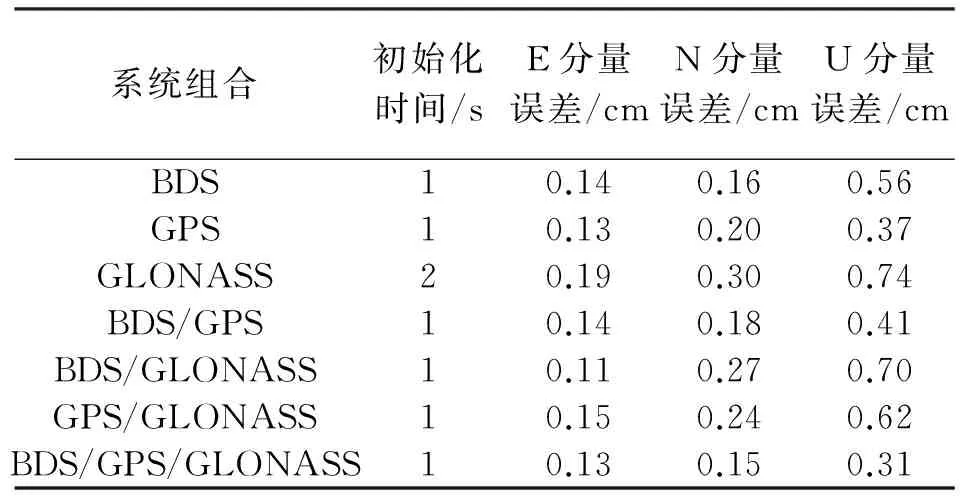
系统组合初始化时间/sE分量误差/cmN分量误差/cmU分量误差/cmBDS10.140.160.56GPS10.130.200.37GLONASS20.190.300.74BDS/GPS10.140.180.41BDS/GLONASS10.110.270.70GPS/GLONASS10.150.240.62BDS/GPS/GLONASS10.130.150.31
由结果可以看出,除GLONASS系统外,其他6种RTK均能在1 s之内完成初始化,并获得平面在0.5 cm、高程精度在2 cm以内的固定解,单系统方面GPS的定位精度优于其他两种系统的定位精度,BDS/GPS/GLONASS组合系统的定位精度要优于其他6种组合方式。
图2表示31 km短基线东、北、高3方向上的坐标误差值,表2为31 km超短基线初始化时间及RMS值。
由结果可以看出,系统组合RTK相对于单系统RTK初始化时间明显缩短,其中BDS/GPS/GLONASS的初始化时间已缩短到3 s,组合系统RTK短基线定位精度相对于单系统没有明显提高。
5 结 语
本文基于附带参数的卡尔曼滤波方法兼容了不同系统的要求,并且根据实测数据解算出各个单系统及4种组合方式下的定位结果。根据分析发现,28 m超短基线条件下, 7种方式除GLONASS外均能在1 s之内初始化完成获得固定解,采用BDS/GPS/GLONASS组合方式能够提高RTK定位精度。31 km短基线条件下BDS/GPS、BDS/GLONASS、GPS/GLONASS、BDS/GPS/GLONASS RTK相对于单系统定位精度提高不明显,但获得固定解时间明显缩短,其中BDS/GPS/GLONASS缩短获得固定解时间最为明显。
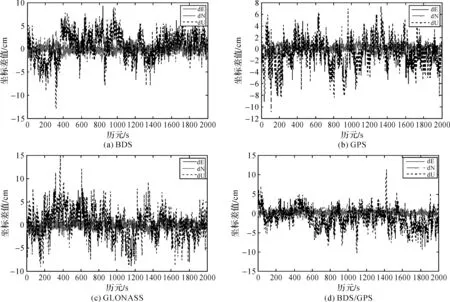
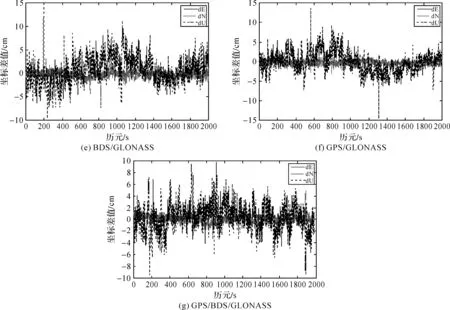
图2 31 km短基线E、N、U方向坐标差值
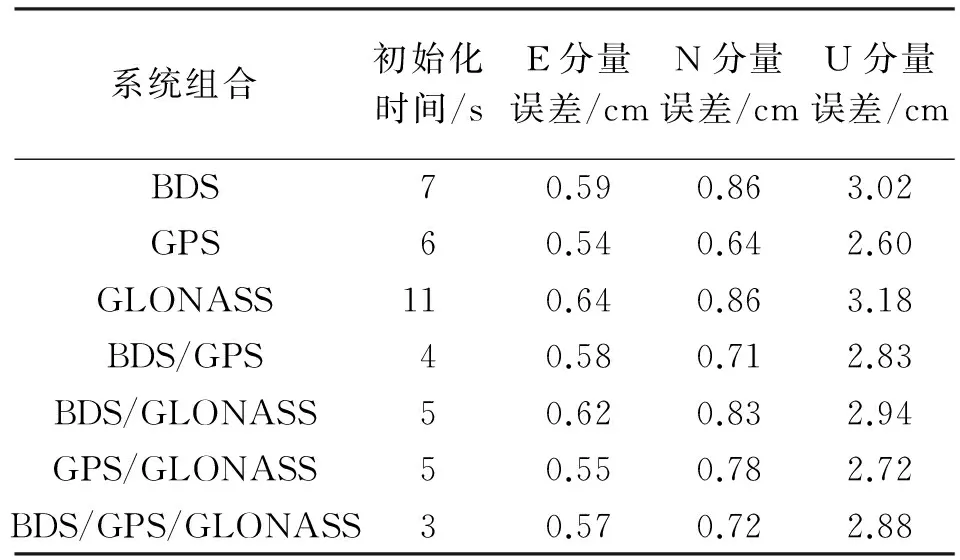
表2 31 km短基线初始化时间及误差RMS值
参考文献:
[1] 汪亮,李子申,袁洪,等.BDS/GPS/GLONASS组合的双频单历元相对定位性能对比分析[J].科学通报,2016,60(9):857-868.
[2] 宋迎春.动态定位中的卡尔曼滤波研究[D].长沙:中南大学,2002:19-26.
[3] 王世进.BDS/GPS-RTK算法研究及软件实现[D].阜新:辽宁工程技术大学,2014:23-26.
[4] 高星伟,过静珺,程鹏飞,等.基于时空系统统一的北斗与GPS融合定位[J].测绘学报,2012,41(5):743-748.
[5] 唐卫明,邓辰龙,高丽峰.北斗单历元基线解算算法研究及初步结果[J].武汉大学学报(信息科学版),2013,38(8):897-901.
[6] SHI Chuang,ZHAO Qile,HU Zhigang,et a1.Precise Relative Positioning Using Real Tracking Data from COMPASS GEO and IGSO Satellites[J].GPS Solutions,2013,17(1):103-119.
[7] LI Jinlong,YANG Yuanxi,XU Junyi,et al.GNSS Multi-carrier Fast Partial Ambiguity Resolution Strategy Tested with Real BDS/GPS Dual-and Triple-frequency Observa-tion[J].GPS Solutions,2015,19(1):5-13.
[8] 李鹤峰,党亚民,秘金钟,等.BDS与GPS、GLONASS多模融合导航定位时空统一[J].大地测量与地球动力学,2013,33(4):73-78.
[9] 祝会忠,高星伟,秘金钟,等.一种GPS整周模糊度单历元解算方法[J]测绘科学,2011,36(4):9-11.
[10]高星伟,李毓麟,葛茂荣.GPS/GLONASS相位差分的数据处理方法[J]测绘科学,2004,29(2):22-24.
[11]蔡艳辉,程鹏飞,李夕银.用卡尔曼滤波进行GPS动态定位[J].测绘通报,2006(7):6-8.
