面向不完备信息系统的双论域决策粗糙集——基于双相对量化信息的角度*

李　敬，王利东

大连海事大学 理学院，辽宁 大连 116026

1　引言

粗糙集理论是由波兰数学家Pawlak于1982年提出的，其是一种有效处理不精确知识的数学工具[1]。目前该理论已经成为人工智能以及计算智能领域刻画不确定信息的主要工具，并且在机器学习、决策分析、模式识别、数据挖掘等领域得到广泛应用。

经典的Pawlak粗糙集建立在等价关系基础上，这限制了粗糙集在实际中的应用。因此学者们不断地对其进行推广，先后建立基于相容关系、优势关系和相似关系等的扩展粗糙集模型[2]。Yao提出邻域系统的粒度计算模型，并应用到知识发现等领域[3]。为提升粗糙集应对噪声数据的适应能力，Wong等人提出了概率粗糙集[4]。Yao等人[5]基于条件概率和两个参数提出了决策粗糙集，并给出有效的方法选择参数阈值。决策粗糙集模型从风险角度对决策过程进行了更深入的刻画。Hu等人[6]在程度粗糙集模型（graded rough set，GRS）[7]和双定量决策粗糙集[8]基础上提出了双相对定量决策粗糙集的相关定义以及性质。Xu等人建立了逻辑“与”、“或”视角下的双定量决策粗糙集模型[8]。对于一个对象，一些属性值可能是缺失的，通常针对这些属性给定一个区分值（即定值）。考虑到信息的不完备性[9]，Yang等人[10]提出不完备信息系统中的多粒度粗糙集。Liu等人在不完备系统建立决策粗糙集模型，并以区间值形式刻画风险参数[11]。Li等人[12]针对不完备信息系统探讨概念认知学习的数学机理。

双论域粗糙集模型是对经典粗糙集模型的一种推广形式，它能够应用于形式概念分析以及决策系统，近年来受到越来越多的关注。例如，Miao等人[13]探讨了双论域上的程度粗糙集以及相应数学性质。杨海龙系统研究了多种形式背景下的双论域粗糙集模型及其数学性质[14]。Dai等人[15]采用粒计算方法定义了双论域上的粗糙集，以及变精度粗糙集。在双论域上，以双相对定量考虑信息缺失问题的粗糙集模型可以从广义程度上刻画不确定信息。本文受文献[6,8,15]的启发，考虑到信息缺失，在不完备信息系统中提出双论域上双相对定量决策粗糙集，并对相应的性质及关系进行了讨论。

本文组织结构如下：第2章介绍相关的知识概念；第3章介绍不完备信息系统中双论域上的双相对定量决策粗糙集定义及相关性质；第4章讨论了两种双相对定量决策粗糙集的关系；第5章用具体实例进一步说明与验证。

2　准备知识

下面介绍相关的基本定义，包括Pawlak粗糙集、概率粗糙集、不完备信息系统、单论域上的概率程度粗糙集和双相对定量决策粗糙集。

2.1　Pawlak粗糙集

定义1[8]设U为非空有限对象集合，R为定义在U×U上的等价关系，等价关系R生成U的一个划分，定义U/R={[x]R|x∈U}，其中[x]R表示x关于R的等价类。对于任意集合X⊆U，X的上下近似定义如下：

相应的，明确包含在X中的对象形成正域，记为明确不包含在X中的对象形成负域，记为或许包含在X中的对象构成边界域，记为

2.2　概率粗糙集

定义2[6](U,R,P)为概率近似空间，对于任意的0≤β<α≤1，X关于概率近似空间(U,R,P)依参数α、β的概率程度上下近似定义如下：

2.3　不完备信息系统

定义3（不完备信息系统）[16]设为一个信息系统，其中U为对象组成的非空有限集合，AT是属性的非空有限集合。若对于每个a∈AT有f:U→Va，其中Va为a的值域，对 ∀a∈AT,∀x∈U,f(x,a)∈Va。如果至少有一个属性a∈AT满足Va含有空值，则称S为不完备信息系统，否则为完备的。

就已有的研究成果来看，不完备信息系统中的空值可以分为遗漏型和缺席型。前者是存在的，但没有记录，而后者被认为是缺席的，是不容许被比较的。

2.4　单论域上的概率程度粗糙集

定义4[6](U,R,P)为概率近似空间，U为非空有限集合，0≤δ<1,X∈P(U)，则基于参数δ，X的概率程度上下近似定义如下：

相应地，X的正域、负域、上边界域、下边界域以及边界域可定义如下：

2.5　单论域上的双相对定量决策粗糙集

双相对定量决策粗糙集是结合程度粗糙集[14]和概率粗糙集模型提出来的，其能从本质上表明相对与绝对定量的结合。

（1）单论域上的第一种双相对定量决策粗糙集

定义5[6]令I=(U,R,P)为概率近似空间，对于参数α、β、δ(0≤β<α≤1,0≤δ≤1)，则第一种双相对定量决策粗糙集（Drq1-DTRS）定义为，其中为X基于参数α、β的下近似，为X基于参数δ的上近似。

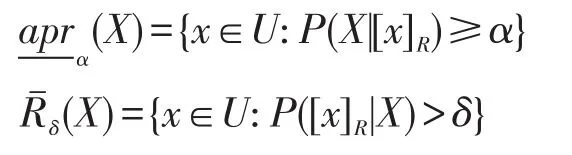
此外X的正域、负域、上边界域、下边界域和边界域分别定义如下：

（2）单论域上的第二种双相对定量决策粗糙集

定义6[6]令I=(U,R,P)为概率近似空间，对于参数α、β、δ(0≤β<α≤1,0≤δ≤1)，则第二种双相对定量决策粗糙集（Drq2-DTRS）定义为，其中为X基于参数δ的下近似，为X基于参数α、β的上近似。

此外，X的正域、负域、上边界域、下边界域和边界域分别定义如下:

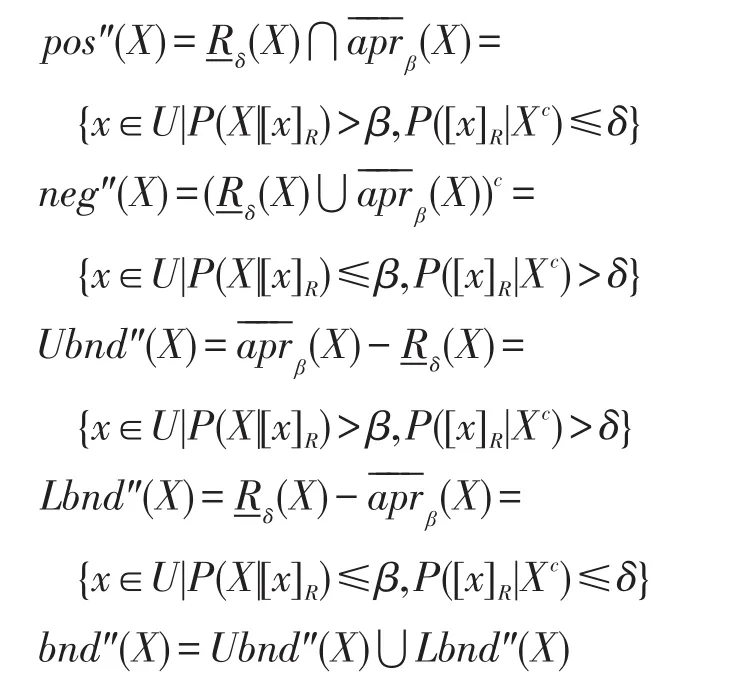
3　不完备信息系统中双论域上的双相对定量决策粗糙集

下面将在不完备信息系统中定义双论域上的双相对定量决策粗糙集模型，并讨论该模型的相关性质。

3.1　不完备信息系统中双论域上的粒度粗糙集模型

在实际生活中，难免会有一些信息缺失，例如文献[12]展示了急性呼吸系统综合征（SARS）病人的数据缺失案例，每位病人都会表现出相应的症状，例如伴有发烧、咳嗽、呼吸困难等。随着时间的推移，部分新患者出现一些新的症状，比如腹泻等，则相应的信息数据也应得以更新，但是对于之前的病人来说这些症状的信息是缺失的。因此考虑到信息缺失，对于论域x∈U，y∈V，对象x可能有症状y，也可能没有。依据此背景给出不完备信息系统下双论域上的粒度粗糙集模型相关定义。

令U、V为两个论域，I⊆(U×V)为论域上的一个二元关系，I(x,y)={1,0,?}，其中I(x,y)=1表示x、y之间一定存在关系，I(x,y)=0表示x、y之间不存在关系，则I(x,y)=?表示在某些情况下不能确定x、y之间是否存在关系[11]。基于此，定义不完备信息系统中双论域上的二元关系R*={(x,y)∈U×V:I(x,y)=1∨I(x,y)=?,∀x∈U,∀y∈V}及其逆关系为R*′={(y,x)∈V×U:(x,y)∈R*}。因此，U中元素x的继承域和V中元素y的前域定义如下：

定义7设U、V为不完备信息系统中的两个论域，论域U到V的关系R*⊆(U×V)及其逆关系为R*′，对于Y⊆V，在双论域上关系R*下Y的上、下近似定义如下：

定义8设U、V为不完备信息系统中的两个论域，论域U到V的关系R*⊆(U×V)及其逆关系为R*′，对于X⊆U，在双论域上关系R*下X的上、下近似定义如下：

3.2　不完备信息系统中双论域上的概率程度粗糙集

本节将给出不完备信息系统中双论域上的概率程度粗糙集的相应定义以及相关性质。

定义9设U、V为不完备信息系统中的两个论域，论域U到V的关系R*⊆(U×V)及其逆关系为R*′，对于Y⊆V，0≤δ≤1，则基于参数δ的Y的概率程度上下近似定义如下：

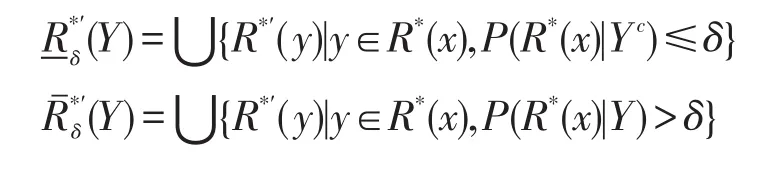
相应Y的概率程度正域、负域、上边界域、下边界域以及边界域为：

由定义9，参数δ取特殊值时，可得如下性质。

性质1对于任意的0≤δ≤1，有以下性质成立：

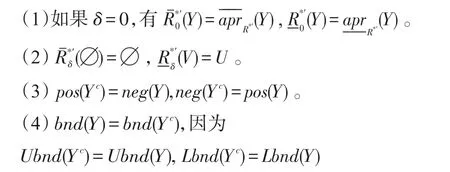
定义10设U、V为不完备信息系统中的两个论域，论域U到V的关系R*⊆(U×V)及其逆关系为R*′，对于X⊆U，0≤δ≤1，则基于参数δ的X的概率程度上下近似定义如下：

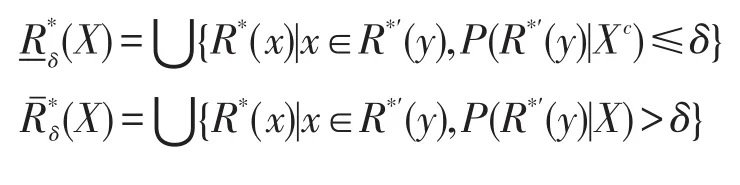
相应X的概率程度正域、负域、上边界域、下边界域以及边界域为：

性质2由定义10，对于任意的0≤δ≤1，有以下性质成立：

3.3　不完备信息系统中双论域上的双相对定量决策粗糙集

一般而言，决策粗糙集模型主要是就相对定量信息来描述近似空间，而程度粗糙集主要描述绝对定量信息[14]。同时从相对量化和绝对量化信息的角度考虑，徐伟华等人提出双定量决策粗糙集。胡宝清等人提出概率程度粗糙集，以及将其与概率粗糙集结合提出双相对定量决策粗糙集。本节考虑到信息的缺失，在不完备信息系统中给出双论域上的双相对定量决策粗糙集的定义，并且对相应的性质进行了讨论。

3.3.1　不完备信息系统中双论域上的第一种双相对定量决策粗糙集

定义11设U、V为不完备信息系统中的两个论域，U到V上的关系R*⊆(U×V)及其逆关系R*′，对于Y⊆V，参数α、β、δ(0≤β<α≤1,0≤δ≤1)，Y的上下近似定义如下：

则不完备信息系统中双论域上对于Y⊆V的第一种双相对定量决策粗糙集定义为

此外，Y的正域、负域、上边界域、下边界域和边界域定义如下：

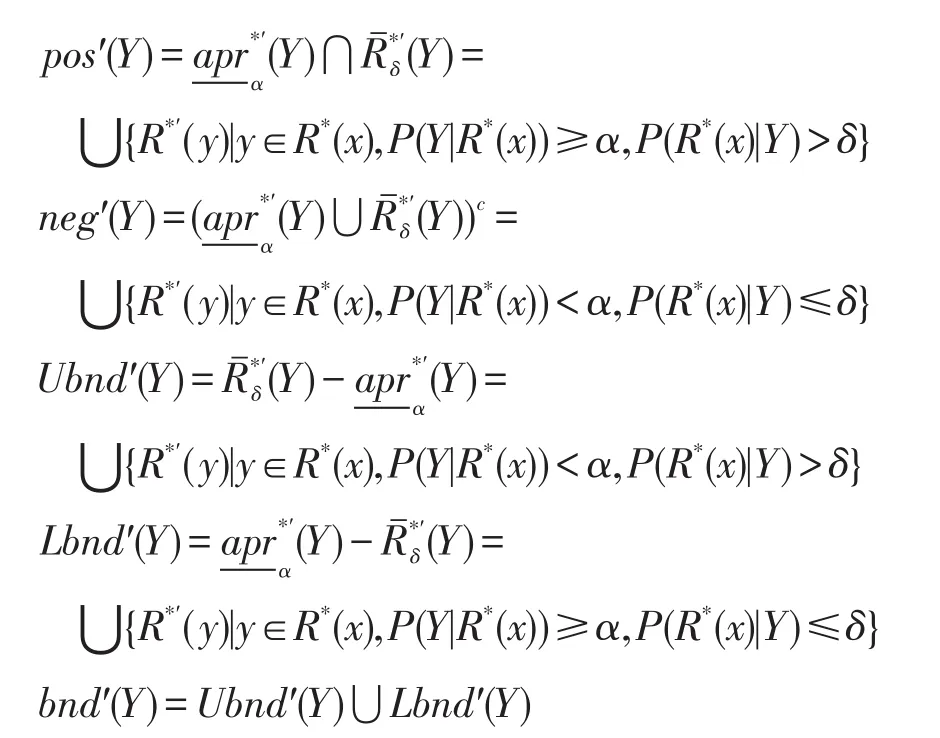
定义12设U、V为不完备信息系统中的两个论域，U到V上的关系R*⊆(U×V)及其逆关系R*′，对于X⊆U，参数α、β、δ(0≤β<α≤1, 0≤δ≤1)，X的上下近似定义如下：

则不完备信息系统中双论域上对于X⊆U的第一种双相对定量决策粗糙集定义为

此外X的正域、负域、上边界域、下边界域和边界域定义如下：

3.3.2　不完备信息系统中双论域上的第二种双相对定量决策粗糙集

定义13设U、V为不完备信息系统中的两个论域，U到V上的关系R*⊆(U×V)及其逆关系R*′，对于Y⊆V，参数α、β、δ(0≤β<α≤1,0≤δ≤1)，Y的上下近似定义如下：

则不完备信息系统中双论域上对于Y⊆V的第二种双相对定量决策粗糙集定义为

此外Y的正域、负域、上边界域、下边界域和边界域定义如下：

定义14设U、V为不完备信息系统中的两个论域，U到V上的关系R*⊆(U×V)及其逆关系R*′，对于X⊆U，参数α、β、δ(0≤β<α≤1, 0≤δ≤1)，X的上下近似定义如下：

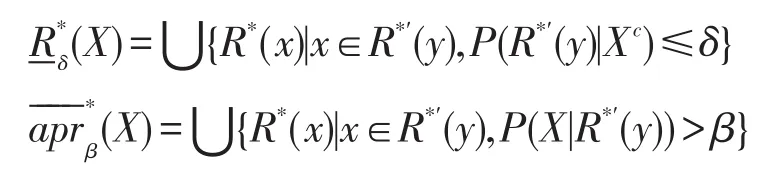
则不完备信息系统中双论域上对于X⊆U的第二种双相对定量决策粗糙集定义为

此外X的正域、负域、上边界域、下边界域和边界域定义如下：

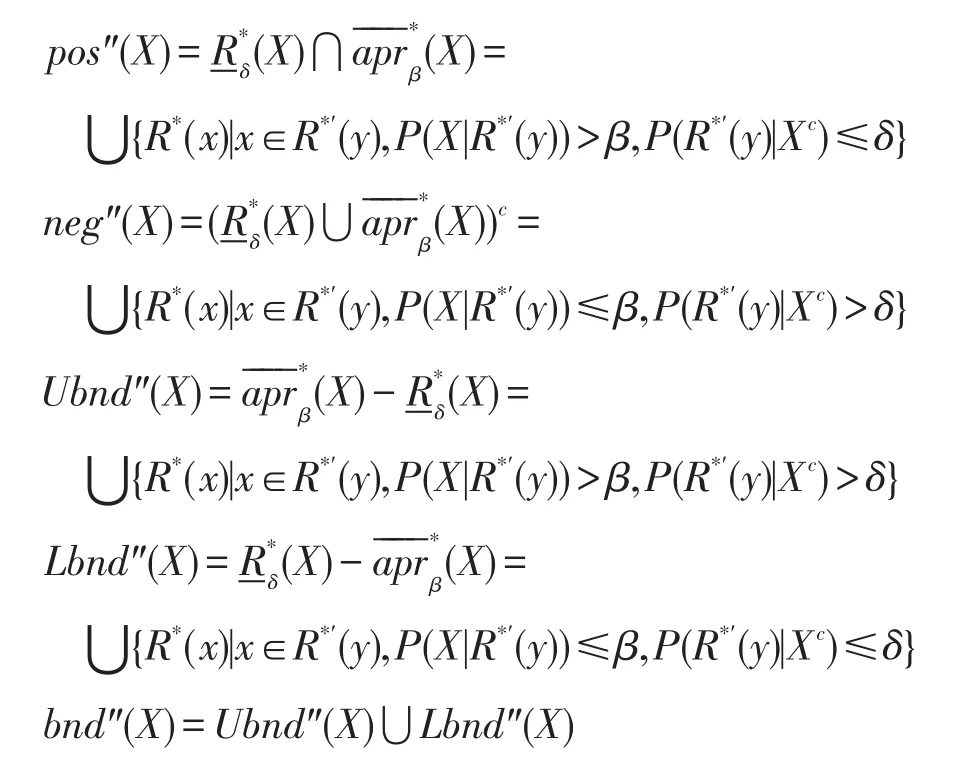
根据以上定义，有以下性质成立。

性质3（1）对于第一种双相对定量决策粗糙集而言，如果α=1,β=0,δ=0，对于Y⊆V，则有 (U,V,；对于X⊆U，则有

（2）相对定量决策粗糙集而言，如果α=1,β=0,δ=0，对于Y⊆V，则有对于X⊆U，则有

证明由定义11～定义14易得证。□

4　第一种双相对定量决策粗糙集与第二种双相对定量决策粗糙集之间的关系

上文给出了在不完备信息系统中双论域上两种双相对定量决策粗糙集的相关定义及性质，在此基础上，下面将在参数α+β与1之间关系的基础上进一步讨论两种双相对定量决策粗糙集的关系。

设U、V为不完备信息系统中的两个论域，论域U、V上给定关系R*⊆(U×V)，R*的逆关系为R*′，对于Y⊆V，参数α、β、δ(0≤β<α≤1,0≤δ≤1)有以下关系。

关系1α+β=1时

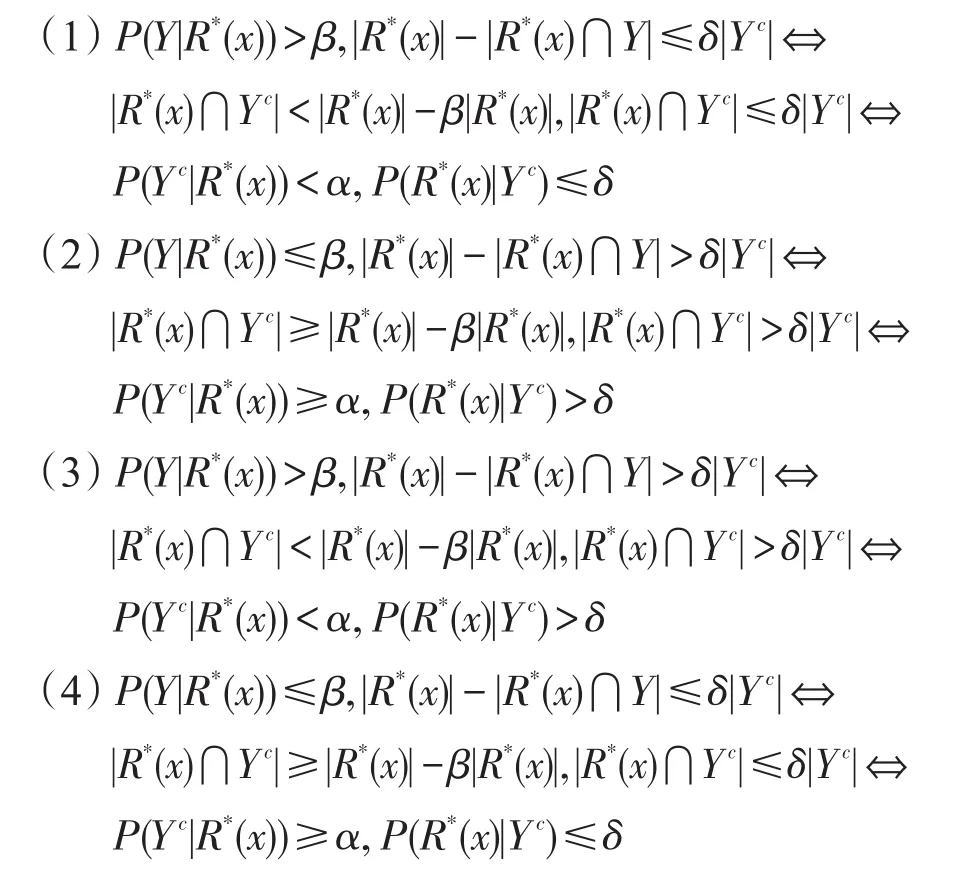
由两种双相对定量决策粗糙集Y的正域、负域、上边界域、下边界域以及边界域的定义可得以下关系：

关系2α+β>1时

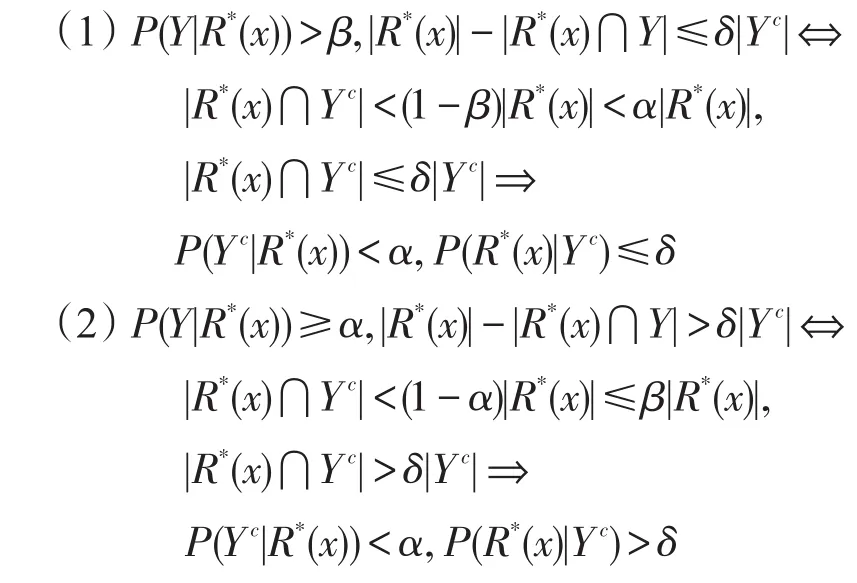
则有pos′(Y)⊆neg″(Yc),neg′(Y)⊇pos″(Yc)。

关系3α+β<1时

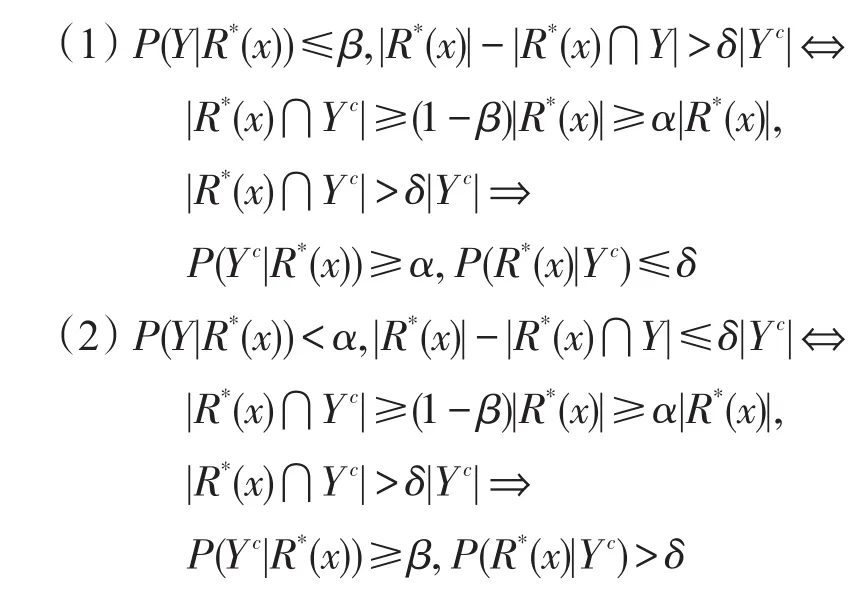
则有pos′(Y)⊇neg″(Yc),neg′(Y)⊆pos″(Yc)。

5　实例分析

本文引用文献[12]中的实例数据来解释两种双相对定量决策粗糙集，并说明它们之间的关系。设(U,V,R*)为一个不完备信息系统（如表1），其中U={x1,x2,x3,x4,x5,x6,x7,x8,x9}为9位患者，症状信息集合V={Fever，Cough，Headache，Difficulty breathing，Diarrhea，Muscle aches，Nausea and vomiting}，为了方便将其记为V={y1,y2,y3,y4,y5,y6,y7}。如果对象xi有症状yj，则I(xi,yj)=1，在表1中值为1，如果对象xi没有表现出症状yj，则I(xi,yj)=0，在表1中值为0。此外，没有记录对象xi是否有症状yj，则记为I(xi,yj)=?。

Table 1　SARS patient information table表1　SARS的病人信息表

由表1的数据，相应地可得：

相应地对于R*′可得：

假设Y={y2,y3,y6}，则Yc={y1,y4,y5,y7}。

（1）取α=0.6，β=0.4，δ=0.6，由定义11可得第一种双相对定量决策粗糙集Y的正域、负域、上下边界域以及边界域如下：

类似的由定义13可得第二种双相对定量决策粗糙集Yc的正域、负域、上下边界域以及边界域如下：

通过以上比较分析可验证文中“关系1”成立，即对于Y的第一种双相对定量决策粗糙集的正域、负域、边界域分别与对于Yc的第二种双相对定量决策粗糙集的负域、正域、边界域相等。

（2）取α=0.6,β=0.5,δ=0.6，同样由定义11可得第一种双相对定量决策粗糙集Y的正域、负域为：

类似的由定义13可得第二种双相对定量决策粗糙集Yc的正域、负域为：

通过以上计算结果的比较可知，第二种双相对定量决策粗糙集Yc的负域包含第一种双相对定量决策粗糙集Y的正域，第一种双相对定量决策粗糙集Y的负域包含第二种双相对定量决策粗糙集Yc的正域。

（3）取α=0.6，β=0.3，δ=0.6，由定义11可得第一种双相对定量决策粗糙集Y的正域、负域为：

类似的由定义13可得第二种双相对定量决策粗糙集Yc的正域、负域为：

通过以上计算结果的比较可知文中“关系3”成立，即第二种双相对定量决策粗糙集Yc的正域包含第一种双相对定量决策粗糙集Y的负域，第一种双相对定量决策粗糙集Y的正域包含第二种双相对定量决策粗糙集Yc的负域。

6　结论

双论域上的粗糙集模型是对经典粗糙集模型的一种推广，本文给出了不完备信息系统中双论域上的粒度粗糙集模型的定义，以及双相对定量决策粗糙集的定义与相关性质，并在此基础上探讨了随着相关参数关系的变化两种双相对定量决策粗糙集的关系。最后以具体实例进一步地解释说明了所提出的定义以及相关关系。

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11(5):341-356.

[2]Greco S,Matarazzo B,Slowinski R.Rough approximation of a preference relation by dominance relation[J].Europe Journal of Operation Research,1999,117(1):63-83.

[3]Yao Yiyu.Perspectives of granular computing[C]//Proceedings of the 2005 IEEE International Conference on Granular Computing,Beijing,Jul 25-27,2005.Piscataway:IEEE,2005:85-90.

[4]Wong S K M,Ziarko W.Comparison of the probabilistic approximate classification and the fuzzy set model[J].Fuzzy Sets and Systems,1987,21(3):357-362.

[5]Yao Yiyu,Wong S K M,Lingras P.A decision-theoretic rough set model[C]//Proceedings of the 5th International Symposium on Methodologies for Intelligent Systems,Knoxville,Oct 25-27,1990.New York:Elsevier Science Inc,1990:17-25.

[6]Fang Bowen,Hu Baoqing.Probabilistic graded rough set and double relative quantitative decision-theoretic rough set[J].International Journal of Approximate Reasoning,2016,74:1-12.

[7]Yao Yiyu,Lin T Y.Graded rough set approximations based on nested neighborhood systems[C]//Proceedings of the 5th European Congress on Intelligent Techniques and Soft Computing,Aachen,Sep 8-11,1997:196-200.

[8]Xu Weihua,Guo Yanting.Generalized multigranulation doublequantitative decision-theoretic rough set[J].Knowledge-Based Systems,2016,105:190-205.

[9]Kryszkiewicz M.Rough set approach to incomplete information systems[J].Information Sciences,1998,112(1/4):39-49.

[10]Yang Xibei,Song Xiaoning,Chen Zehua,et al.On multigranulation rough sets in incomplete information system[J].International Journal of Machine Learning and Cybernetics,2012,3(3):223-232.

[11]Liu Dun,Liang Decui,Wang Changchun.A novel threeway decision model based on incomplete information system[J].Knowledge-Based Systems,2016,91:32-45.

[12]Zhao Yingxiu,Li Jinhai,Liu Wenqi,et al.Cognitive concept learning from incomplete information[J].International Journal of Machine Learning&Cybernetics,2016,7(4):1-12.

[13]Liu Caihui,Miao Duoqian,Zhang Nan.Graded rough set model based on two universes and its properties[J].Knowledge-Based Systems,2012,33:65-72.

[14]Yang Hailong.The theory and method of rough sets on two universes[M].Beijing:Science Press,2016.

[15]Dai Jianhua,Han Huifeng,Zhang Xiaohong,et al.Catoptrical rough set model on two universes using granule-based definition and its variable precision extensions[J].Information Sciences,2017,390:70-81.

[16]Qian Yuhua.Granulation mechanism and data modeling for complex data[D].Taiyuan:Shanxi University,2011.

附中文参考文献：

[14]杨海龙.双论域粗糙集理论与方法[M].北京:科学出版社,2016.

[16]钱宇华.复杂数据的粒化机理与数据建模[D].太原:山西大学,2011.