Bergman-Hartogs域上的两类双全纯映照子族

王朝君，崔艳艳，刘　浩

(1.周口师范学院数学与统计学院，河南 周口 466001； 2.河南大学现代数学研究所，河南 开封 475001)

1　预备知识

1995年，Roper-Suffridge算子的引入在单变量解析函数与多复变量双全纯映照之间架起了一座桥梁，也为在多复变空间中构造具有特殊几何性质的双全纯映照提供了保障.双全纯映照及其延拓主要研究各类双全纯映照子族，而随着各类双全纯映照子族的不断出现，其在Roper-Suffridge延拓算子下的几何不变性引起了众多学者的关注.

本文将Roper-Suffridge延拓算子进一步推广为

F(w，z)=(w(1)(f′(z1))δ1，…，w(s)(f′(z1))δs，f(z1)+G([f′(z1)]γz0)，(f′(z1))γz0)′.

(1)

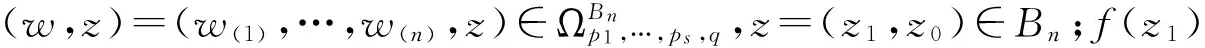
F(z)=(f(z1)+G([f′(z1)]γz0)，(f′(z1))γz0)′.

(2)

下面主要讨论算子(1)在域

上保持α次β型螺形映照及复数λ阶殆星映照的性质，并得到算子(2)也具有同样性质.

引理1[1]设Ω∈Cn是有界星形圆形域，其Minkowski泛函ρ(z)除去一个低维流形Ω0外一阶可导，则∀z=(z1，…，zn)∈ΩΩ0，

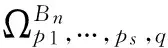
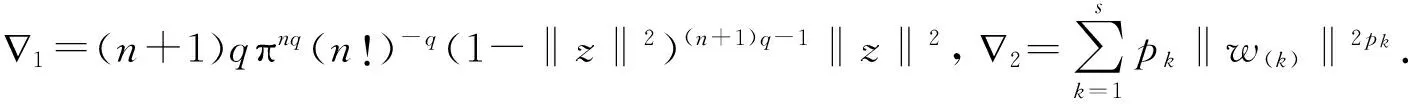
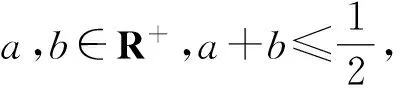
引理4[3]设f(z)是单位圆盘D上的正规化双全纯函数，α≥2，则

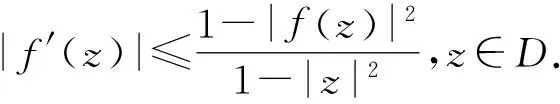
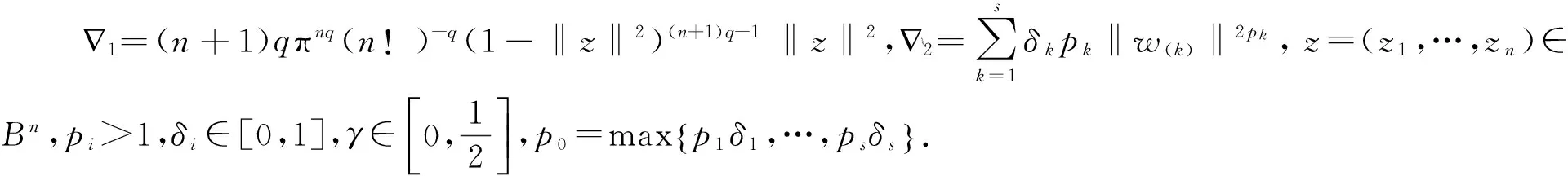
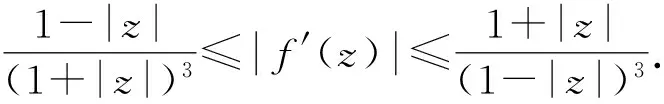
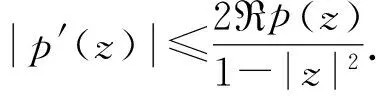
2　主要结论及其证明

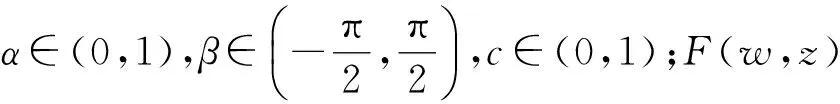
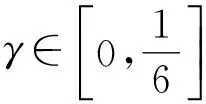
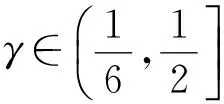
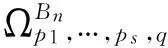
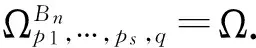
(3)

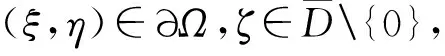
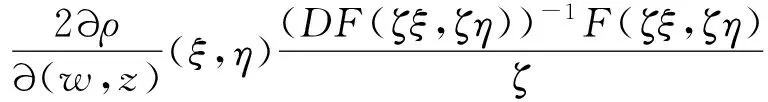
由引理2得

(4)

其中

令

(5)

则q(z1)∈H(D)，|q(z1)|<1且

(6)

(1+2)I=2α(1-itanβ)G(w，z)+(i2αtanβ-1)(1+2)=

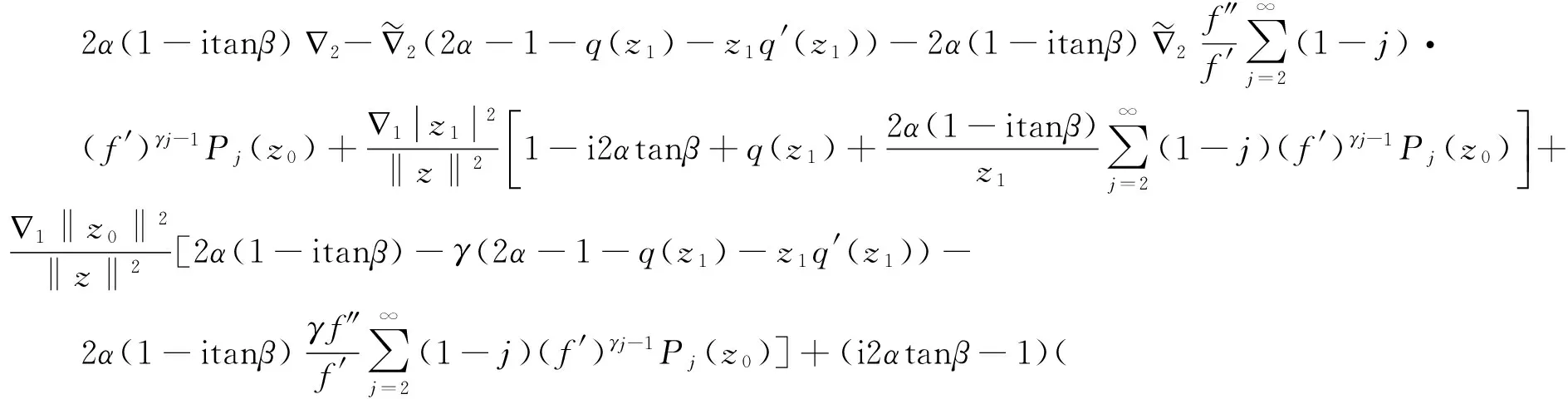
(7)

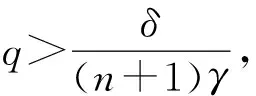
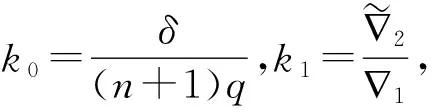
(8)

从而由(7)—(8)式及引理5―7得

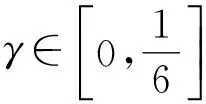
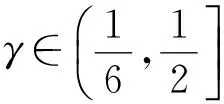
注1在定理1中若只考虑算子(1)中的后两个元素，则得到算子(2)在单位球Bn上也保持α次β型螺形性.若令β=0，则得到相应的关于α次星形映照的结论.

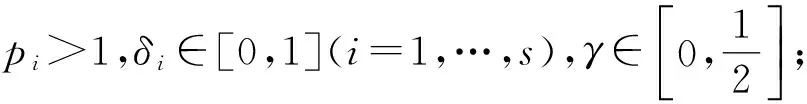
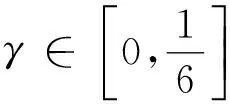
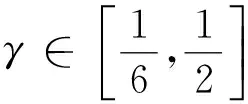
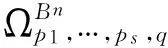
证明由复数λ阶殆星映照的定义，只需证明

(9)

(10)

由f(z1)是D上的复数λ阶殆星函数知Req(z1)>0，q(z1)∈H(D)，q(0)=1且

(11)

由引理8，

(12)

根据(4)，(10)与(11)式，

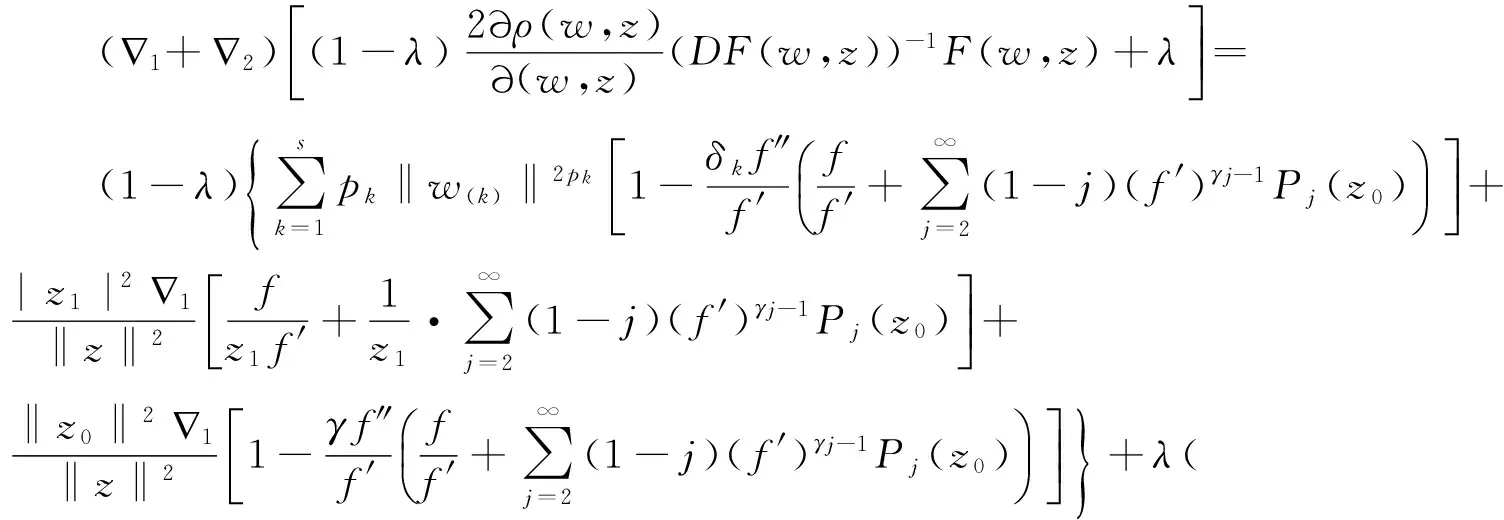
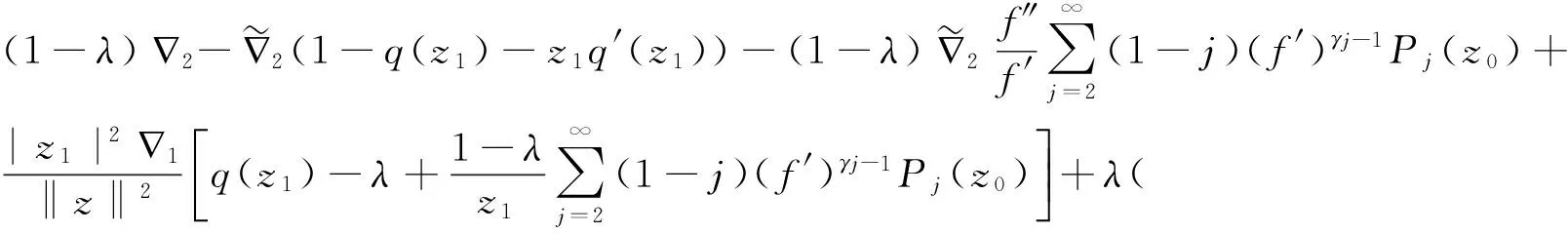
与定理1类似论证可得结论成立.

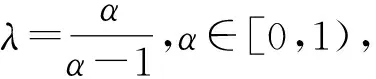
[参考文献]

[1]LIU T S，REN G B.Growth theorem of convex mappings on bounded convex circular domains[J].Science in China，1998，41(2)：123-130.

[2]唐言言.Bergman-Hartogs型域上的Roper-Suffridge算子[D].开封：河南大学，2016.

[3]MUIR J R.A class of Loewner chain preserving extension operators[J].J Math Anal Appl，2008，337(2)：862-879.

[4]AHLFORS L V.Complex analysis [M].3rd ed.New York：Mc Graw-Hill Book Co，1979：123-128.

[5]DUREN P L.Univalent functions[M].New York：Springer-Verlag，1983：57-58.

[6]GRAHAM I，KOHR G.Geometric function theory in one and higher dimensions[M].New York：Marcel Dekker，2003：27-32.