频率源对雷达测速精度影响分析

杨　博，梁允峰，孟联文，杜培明，张永胜

(太原卫星发射中心，太原 030031)

0　引　言

在航天靶场无线电测控系统中，为获得更好的测速精度(降低随机误差和系统误差)，测速雷达要求较高的频率源稳定性和准确性[1-2]，目前常用的是铷钟频率源[3]。国内外对于频率源模型[4-5]及铷钟频率源对无线电跟踪精度影响的研究[6-8]已开展得比较深入，文献[2]建立双向多普勒测速的简化频率流程，分析了频率源短稳及各相干振荡器的短稳对测速随机误差的影响；文献[3]研究了铷钟校频原理，提出了多参考源的铷原子钟校频方案；文献[5]讨论了震动对时频的影响和对测速误差的影响；文献[6]采用双向跟踪模式建立多普勒测速跟踪系统模型，推导了阿伦方差、取样时间以及电波往返传输时间与地面站系统多普勒测速精度的关系；文献[7]讨论了本振相位噪声对雷达系统的影响因素，并提出合理的相位指标参数；文献[8]利用高速鉴相器和VCOCXO组成精密锁相环路，实现超高稳频率源，已应用于测速雷达系统。但上述文献中模型只是从仿真角度进行了校验，没有结合雷达实际测量数据分析，并且没有考虑时钟切换的影响。文献[9]针对星载原子钟，提出数字锁相环和直接频率合成的频率源切换方案，但针对测控雷达的相关研究并不多。本文建立了基于频率源分析雷达测速精度理论模型，采用同步校频和互备双锁相环的新方法实现高稳定和高精度的铷钟频率源，提升频率源准确度、稳定度和可靠性；并通过静态试验和动态试验数据分析频率源基准幅度、频偏、准确度和稳定度对雷达测速多普勒及测速精度的影响。

1　理论分析

1.1　频率源模型

频率源的频率起伏包括确定性部分和随机性部分，确定性部分与频率准确度相关，频率准确度表示振荡频率偏离标称频率f0的程度，随机性部分与短期稳定性有关，在时域可以用阿伦方差[4]表示。在频域可以用幂律谱噪声模型[5]表示，用信号相位噪声表征，时域的稳定度和频率域相位噪声转换关系如表1所示。

表1　相位噪声与短稳的换算公式Table 1　Short-term stability versus phase noise

其中，τ为测量间隔时间，y为Δf/f0，f0为载波频率，fm为载波边带频率，即测量频率相对载波频率的频偏，fB为测量系统带宽；(fm)为不同频偏下相位噪声,σyi(τ)为不同斜率频偏分量fm时的短稳分量，m表示相位噪声曲线斜率。σYI(τ)为综合短稳结果，如下所示：

σYI(τ)=

(1)

1.2　频率源影响测速模型

测速雷达系统中，分析频率源对测速多普勒影响如图1所示，其中T表示发射天线，R表示接收天线，发射频率基准ft 0，接收频率基准fr 0，上变频系数Ku，下变频系数Kd，λ为接收信号的工作波长，雷达主站发射出由原子钟上变频产生的发射信号(频率fT)后，经应答机[1]接收(频率fsR)锁相倍频，转发(频率fsT)下传,N为应答机频率转发比，雷达接收频率fR，包含上行通路和下行通路多普勒信息，接收基准频率fR 0,fR 0不包含多普勒信息，多普勒信息为fd，推理可知，多普勒可用下式表示:

fd=fR-fR 0=N(Kuft 0)(1-2v/c)-Kdfr 0=

Kd(ft 0-fr 0)-Kdft 0(2v/c)

(2)

图1　频率源测速模型Fig.1　The Doppler diagram versus frequency source

1.3　测速精度分析

测速精度主要包括随机误差和系统误差，随机误差主要包括频率源不稳、电源有规干扰和杂波干扰、热噪声误差、测速终端量化噪声等引入的误差[11]，本文主要讨论频率源不稳对发射和接收信道带来的误差影响。

假设10 MHz频率源短稳指标为σy(τ1)，τ1为测量间隔时间，接收本振信号和发射信号均由10 MHz频率源倍频、变频和放大产生，其短稳指标变为σy1(τ1)。则频率源不稳定度引起的测速相位误差为式(3)，折算到速度误差上如式(4)所示：

(3)

(4)

式中:σφ1为相位误差，fR=Kdfr 0+fd为接收频率，τ为积分时间，λ为信号波长，σv为测速误差，发射信号与接收信号引入相位误差计算方法相同。

测速系统误差主要包括发射信道相位漂移、接收信道相位漂移和测速终端相位漂移误差[12]；如果收发同源，则ft 0=fr 0，由式(2)可知，fd=-2Kd·fr 0v/c=-2fR 0v/c，v=-cfd/(2fR 0)。如果收发不同源(副站)，fd包含收发频率源不一致导致的系统差Kd(ft 0-fr 0)，其中(ft 0-fr 0)为发射和接收两站间频标相对偏差，c为光速，引入测速系统差Δv如下所示：

Δv=-c(ft 0-fr 0)/(2fr 0)

(5)

2　高稳频率源设计

文献[8]和[10]中频率方案采用锁相环和高稳晶振提升频率源短稳，文献[3]提出基于电子计数法的校频方案，文献[13]提出卡尔曼滤波铷钟跟踪算法，方案相对复杂，本文高稳频率源方案如图2所示，本地基准首先经过高频内插方法同步校频提升基准准确度，然后和外部基准同时送选择开关，经过分路后同时送互为备份的时频锁相环A,B，通过锁相环和高稳晶振提升频率源短稳，然后分路输出至雷达各分系统。外部频率源(外10 MHz)准确度和稳定度由外部铷钟确定，本地时频基准(内10 MHz)选用FEI5650A铷原子频标[14]。增加了内外基准控制开关和频标选择开关，实现频率源和锁相环频标的自动和手动切换。外部基准和内部基准通过基准选择开关实现互备和自动切换，锁相环通过标频选择开关实现互备和自动切换。

图2　高稳频率源方案Fig.2　Diagram of high stability frequency source

2.1　同步校频

同步校频接收外部1 pps的信号，与本地铷钟频标进行相位比较，完成对本地频标的校准，输出稳定的频率信息。主要有本地铷钟、精密相位检测与测量、信号检测判别等部件组成，如图3所示。

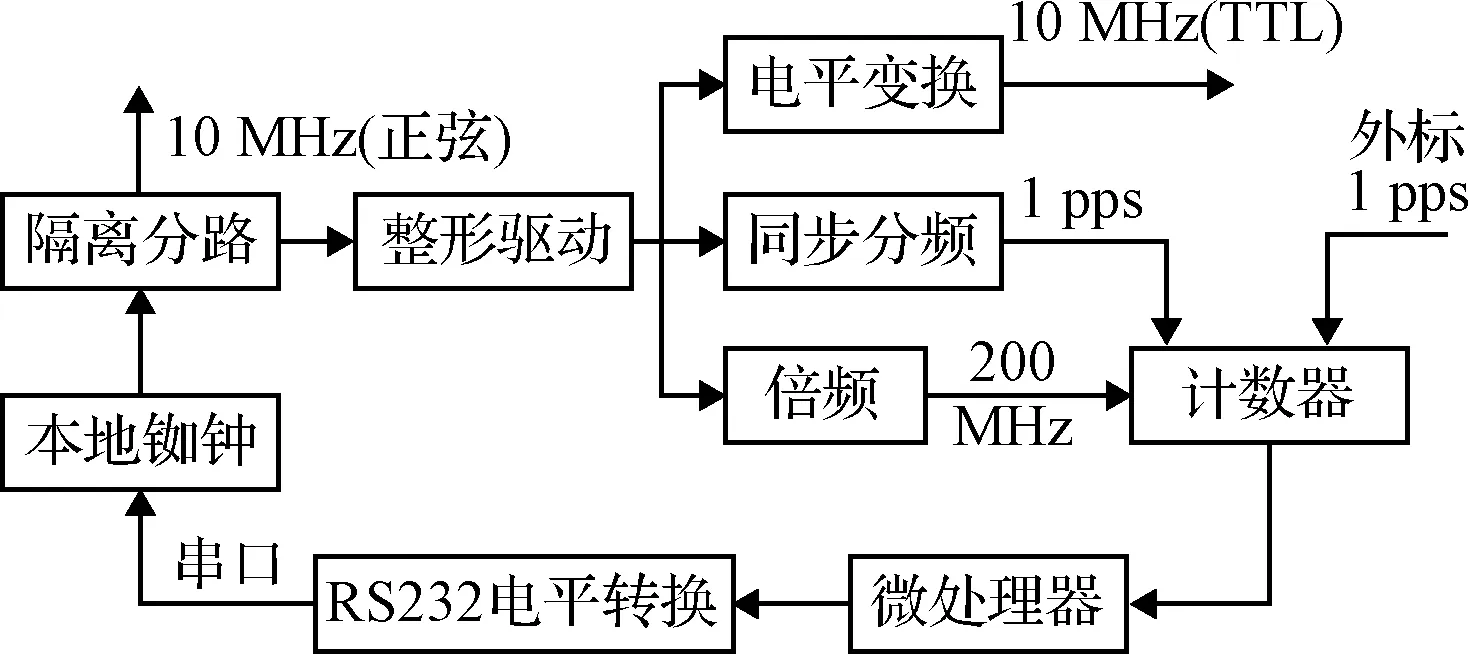
图3　同步校频模块原理图Fig.3　Diagram of sync frequency calibration

1)采用高频脉冲内插方法确定相位差，即用高频脉冲插入到两个信号之间的相位差脉冲中，通过读取内插高频脉冲个数，得到相位差脉冲的宽度，高频脉冲频率越高，测量精度越高，选用ALTERA公司的Cyclone系列EP1CT144I7芯片，利用其内部倍频器输出200 MHz信号，精度可达5 ns。

2)微处理器在FGPA芯片中实现，主要功能是检测输入信号和输出信号状态，检测同步校频工作状态并给出指示，读取并储存相位差数据，计算直接数字频率合成(DDS)控制值并调整DDS输出。选用的FE5650A铷原子频率源集成了48位DDS功能，外部设置有串行接口，微处理器通过串行接口设置并读取DDS控制量，其调整范围为±383 Hz。

3)控制软件中断检测程序主要读取相位差数据和状态控制字，根据自由运行、保持和外部1 pps同步三种情况计算对应的DDS并输出，结束后返回，下次中断信号启动时，重新判断处理。

2.2　互备双锁相环设计

锁相环模块原理框图如图4所示，采用双D触发器74F74作为鉴相器，其为TTL电路，器件低噪较低，完成通道鉴相和产生锁定指示，此外还送出停振指示和锁定指示信号。采用OSA公司8607BVA[15]系列超高稳晶体振荡器，在没有外部频率基准信号时，为晶体振荡器的自由振荡输出。采用精密运算放大器OP27组成有源比例积分滤波器，具有平滑输出和低通滤波的作用，由于VCOCXO的相位噪声指标比频率参考源指标高，在环路设计时尽量窄带宽，按照3 Hz带宽设计。此外，对鉴相器和环路滤波器采用低噪稳压电路供电，避免电源间的相互串扰。

图4　锁相环模块原理图Fig.4　Diagram of phase-locked loop

锁相环自动切换设计由选择开关控制电路和选择开关两部分组成，开关控制电路对锁相环A和B的VCOCXO停振状态进行判断，输出相应的控制信号(高/低电平)给选择开关，选择开关根据控制信号来选通相应的锁相环路信号进行输出。当一路信号停振时，自动切换另一路信号，增强频率源工作可靠性。

3　试验分析

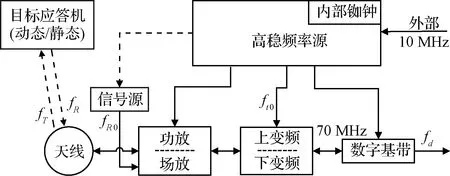
图5　频率源试验的原理图Fig.5　The diagram of radar via frequency source

测速雷达频率源试验如图5所示，高稳频率源分路成多路10 MHz标频信号，送至下变频、基带等分系统。主站(带发射分系统)利用10 MHz标频信号通过上变频产生上行信号，经功率放大后从天线发出，至应答机并下行转发，图中信号源型号为安捷伦ESG系列信号产生器E4428C[16]。

3.1　频率源指标分析

首先计算自由振荡条件下8607系列VCOCXO短稳，利用测试的相位噪声数据，如表2所示，频率源f0为10 MHz，fm为载波频率偏移，分别取1 Hz,10 Hz和100 Hz，fB为测量系统带宽，取值10000 Hz； 1(fm)为不同频偏下相位噪声，如文献[15]所示，VCOCXO在偏移1 Hz,10 Hz和100 Hz时相位噪声分别为-125 dBc,-145 dBc,-153 dBc，利用表1中公式计算短期稳定度，在测量间隔时间为10 ms时，VCOCXO自由振荡短期稳定度为9.9×10-12。利用相同方法，根据表2中锁相环各环节相位噪声数据，可知外10 MHz参考频率源短稳为5.15×10-11，锁相环输出信号的短稳为1.02×10-11，可以看出锁相环对频率源稳定度提升5倍左右。

表2　锁相环各环节相位噪声Table 2　Phase noise of each part of the phase-locked loop

用相位噪声测试仪PN9000[17]测试，在测量间隔时间为10 ms时，经过锁相环后，10 MHz短稳1.80×10-11，本地铷原子钟校频到GPS/GLONASS或北斗导航系统的基准上，准确度-5.2×10-12,满足指标要求2×10-11；同时测试，接收机本振信号短稳2.28×10-11，准确度1.5×10-11，发射信号短稳2.92×10-11，准确度-3.56×10-11，满足指标要求5×10-11。

3.2　多普勒分析

用信号源模拟下行信号，信号源连接基准源，测试同源情况下测速精度情况，如果信号源不连接基准频率源，测试非同源情况下测速精度，输出点频信号fR，雷达接收电平设置为-120 dBW，每10分钟记录一组数据，观察分析多普勒记录数据。

3.2.1频率源幅度和频率偏移对多普勒影响

首先测试10 MHz基准频率源信号幅度对测速雷达的影响，10 MHz基准频率源幅度指标为450 mV，改变信号源输出10 MHz信号的幅度，从500 mV逐渐变到60 mV后，时频锁相环失锁，报故障状态，说明10 MHz信号幅度在60 mV以上时，测速雷达可以正常工作。反之，从60 mV增大至最大1000 mV，雷达系统均能正常工作。

信号源用内部的基准，外部频率源输出10 MHz信号，测试外10 MHz信号频偏1 Hz,0.5 Hz,0.2 Hz,0.1 Hz和0.05 Hz情况下多普勒变化情况，图3为外部10 MHz频偏0.2 Hz时多普勒数据偏差情况。具体试验数据如表3所示，频偏为0时雷达多普勒为-10 Hz，是由信号源非同源导致，同源时频偏接近0 Hz，频率源负偏时测试结果相似。

表3　10 MHz频偏对多普勒数据的影响Table 3　Doppler versus deviation of frequency source

图6　频率源多普勒试验结果Fig.6　The Doppler result versus the frequency source

3.2.2时频锁相环对多普勒影响

将外10 MHz信号经过基准10 MHz选择分路模块，其中一路10 MHz信号甩开锁相环A直接送测速雷达通道1，另一路10 MHz信号输入到锁相环B，锁相环B输出10 MHz信号直接送测速雷达通道2，然后再切换内外10 MHz基准信号，两通道多普勒数据变化曲线如图6所示。

如图6(b)所示，实线表示测速雷达通道1多普勒，其10 MHz频率源甩开锁相环，虚线表示测速雷达通道2多普勒，其10 MHz频率源经过锁相环。当输入频率源不经过锁相环时，测速多普勒快速恢复到0 Hz附近，而当频率源经过锁相环时，测速多普勒经过一个稳态跳变后再开始振荡收敛达到稳态，经过多次试验，跳变幅度不规律，试验中分别出现-84 Hz,-187 Hz等值，持续时间为1～3 s。

为进一步讨论多普勒跳变现象，检测锁相环开环晶振固有频率，即鉴相电压最大和最小时输出的频率，由于测试10 MHz信号比较困难，所以仍采用多普勒频率偏差情况来衡量，试验条件为将内、外10 MHz基准信号全部断开，用锁相环超稳晶体振荡器的固有频率作为基准信号，测试锁相环鉴相电压。锁相环A,B的最大鉴相电压为9.93 V，最小鉴相电压为0.7 V，分别对应的多普勒偏差如表4所示。

表4　OCXO固有频率对多普勒的影响Table 4　The maximum/minimum Doppler of free-running OCXO

由表4可知，测速雷达时频锁相环A带宽范围内对应多普勒范围为[-186,107]Hz，锁相环B带宽范围内对应多普勒范围为[-84,178]Hz,在此范围内频率源频偏与多普勒成近似线性对应关系。超出此范围后可能导致环路失锁，失锁后或重新锁定过程中，多普勒会被限制在锁相环固有频率对应的多普勒频率上，持续一段时间后重新趋于稳定。

3.3　测速随机误差分析

如图5所示，信号源用内部的基准，测试非同源情况下测速方差；信号源与雷达频率源的10 MHz同步时，测试接收信道同源情况下测速随机差情况；此外利用主站设备对应答机发射上行信号，同源接收机接收应答机转发的下行信号，测试收发同源时测速随机误差。测试时雷达接收电平为中电平(-120 dBW)。

3.3.110 MHz频率源影响

由第3.1节的讨论可知，10 MHz频率源短稳指标为2×10-11(采样测量时间为10 ms)，外10 MHz频率源的短稳好于内10 MHz的短稳，对应的接收本振和发射信号短稳指标为5×10-11(采样测量时间为10 ms)，根据式(3)计算频率源不稳定度引起的测速相位误差，其中fR接收频率取5xxx MHz，fT发射频率为5xxx MHz，积分时间τ为50 ms，采样测量时间τ1为10 ms，σy1(τ1)=5×10-11，计算可得接收和发射引入的相位误差分别为2.3°和2.1°，根据式(4)折算到速度误差上为0.0088 m/s和0.008 m/s，合成运算后折合误差0.0119 m/s，测速雷达测速误差指标0.02 m/s，其它为热噪声和量化噪声等。

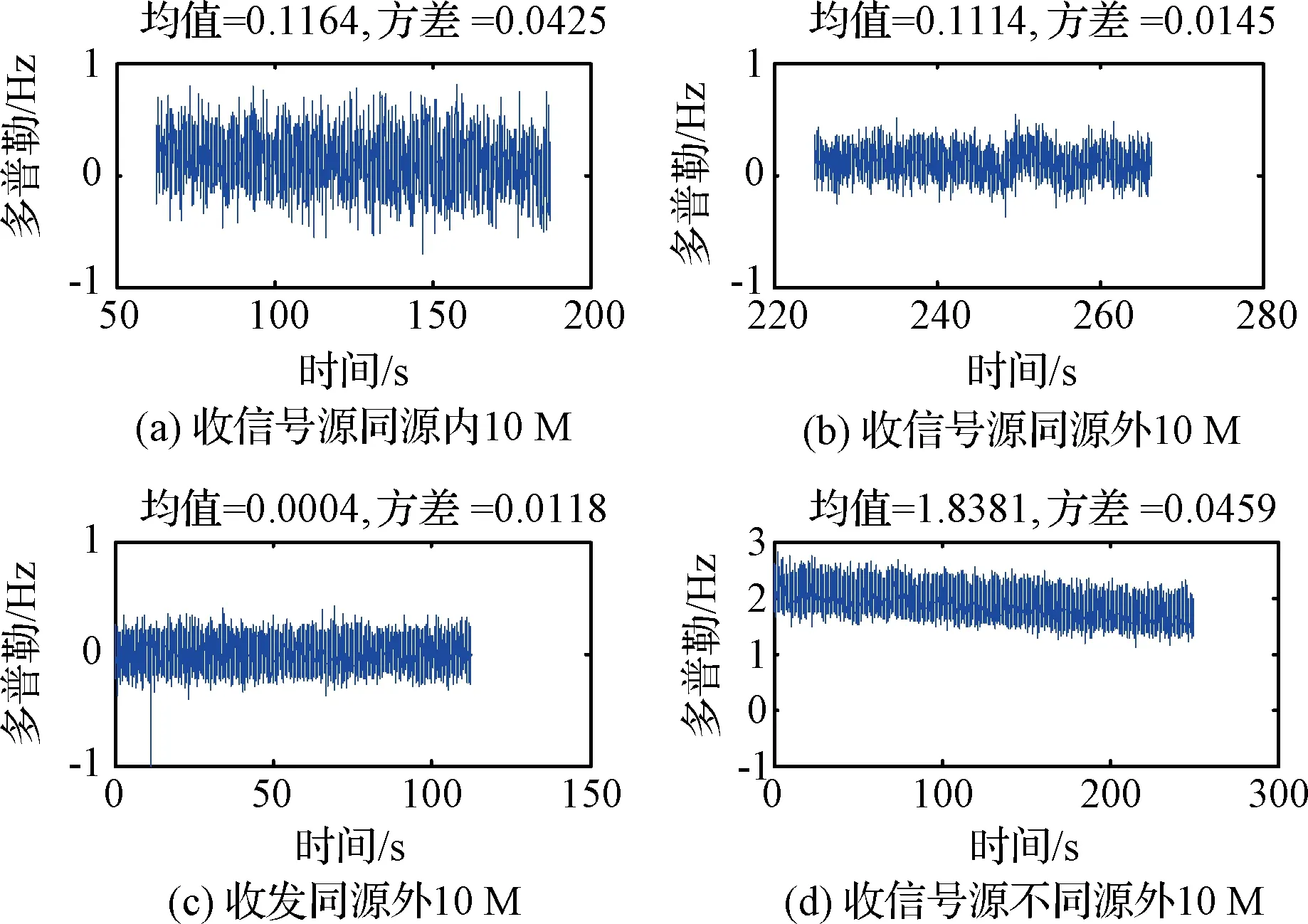
图7　多普勒、均值和方差Fig.7　Doppler, mean and variance of Doppler

不同情况下测试结果如图7所示，图7(a)表示内10 MHz频率源接收雷达与信号源同源情况下多普勒数据；图7(b)表示外10 MHz频率源接收雷达与信号源同源情况下多普勒数据；图7(c)表示外10 MHz频率源发射和接收雷达同源情况下多普勒数据；图7(d)表示外10 MHz频率源接收雷达与信号源不同源情况下多普勒数据，通过统计方法求均值和方差如表5所示。

表5　内外10 MHz源对多普勒随机差的影响Table 5　The mean and variance of Doppler

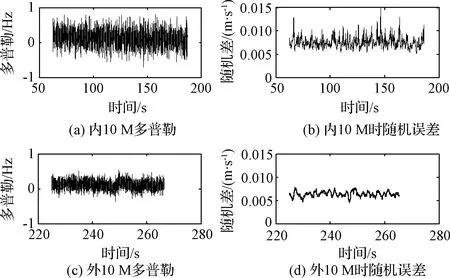
图8　内、外10 MHz下多普勒和测速随机差Fig.8　Doppler and velocity variance with different frequency sources

利用最小二乘方法分别计算接收同源情况下随机误差，多普勒数据采样率为80 Hz，最小二乘法采用80点拟合，三阶最小二乘方法，计算结果如图8所示。由图8可知，外10 MHz情况下测速随机差较好,在0.005～0.007 m/s范围内，内10 MHz情况下随机误差跳变较大，范围在0.005～0.015 m/s，在第3.1节中外10 MHz比内10 MHz短稳指标好，相应的外10 MHz时测速随机误差较小。

图9　经过与甩开锁相环时多普勒和测速随机差Fig.9　Doppler and velocity variance when the frequency source with the PLL or without the PLL

3.3.2锁相环影响

锁相环之前的频率源短稳指标为1×10-10(采样测量时间为10 ms)，经过锁相环后短稳指标为2×10-11(采样测量时间为10 ms)，在信号源非同源情况下分别测试外10 MHz频率源经过时频锁相环和不经过时频锁相环时的多普勒，记录数据后利用最小二乘方法，计算测速随机差，结果如图9所示，从图9(a)和图9(b)可知，甩开锁相环时多普勒跳变较大，测速随机差在0.02 m/s左右，如图9(c)和图9(d)所示，经过锁相环多普勒跳变较小，测速随机差在0.01 m/s左右，所以锁相环能够降低多普勒测速随机差。

3.4　测速系统误差分析

3.4.1静态试验

在第3.3.1节的试验中，测试内外10 MHz频率源在接收同源、收发同源和接收不同源情况下的多普勒情况，用多普勒均值来分析静态测速雷达系统差。如表5所示，收发同源外10 MHz情况下，测速多普勒均值为0.0118 Hz，反映了测速雷达发射机通道、应答机转发通道和接收机通道的系统误差；接收同源情况下测速多普勒均值均小于0.012 Hz，反映了接收信道和信号源同源情况下的系统误差，接收非同源时，测速多普勒均值为1.8381 Hz，反映了信号源在非同源情况下的测速系统误差。分析可知，收发不同源时，其导致的系统误差远远大于其它系统误差分量。

3.4.2动态试验

某次跟踪测量任务中，应答机安装在飞行器上，测速雷达跟踪动态目标，时频锁相环由主用A切换到备用B，导致测速设备多普勒跳变，如图10(a)所示，测速雷达多普勒一阶差分在相对时60 s左右振荡明显，而后振荡逐渐消失，其它时间点多普勒一阶差分跳变是由于特征事件影响。

图10　动态试验时多普勒一阶差分和系统误差Fig.10　The difference of Doppler and the velocity systematic error when the frequency source PLL switch

将多套测速测量设备事后分析目标最优弹道[18]作为真值，反算本雷达速度偏差作为系统误差。在频率源切换时间段，在相对时间55 s到59 s测速数据系统误差出现跳变，如图10(b)所示，系统误差为-6 m/s，持续时间4 s，基本为常值误差，固定偏差折算到多普勒为107 Hz，之后残差从6 m/s振荡减小渐渐趋于0 m/s，在60 s到76 s之间有抖动，之后系统误差趋于平稳。从上述分析和表5中数据可以看出，时频锁相环A从最小电压处失锁，失锁后系统自动切备用锁相环B，导致测速雷达多普勒跳变，对应时频跳变幅度超过锁相环限幅值107 Hz左右，被限幅几秒后，振荡逐渐消失，时频锁相环切换导致雷达测速环路重新锁定并限幅的综合结果。

4　结　论

本文通过高频内插同步校频和双锁相环路加高稳晶振实现了高稳频率源，使测控雷达保持了较高的测控精度。通过理论分析和试验校验，在一定频偏范围内，10 MHz源频偏和雷达多普勒频偏成近似线性对应关系；雷达测速随机差与参考源短稳相关，通过锁相环加高稳晶振能够显著提升参考频率源短期稳定度，进而降低雷达测速随机差；同步校频可以减小本地铷钟频率源和外部基准的频差，从而减小内部基准时测速系统差，没有同步校频或接收不同源时，其导致的系统误差远远大于其它系统误差分量。双源和双锁相环存在源切换和锁相环切换问题，通过自动切换设计，增强了高稳频率源可靠性。相关结论对改进铷钟频率源的设计，对认识频率源对多普勒和测速精度影响有一定参考价值。

[1]凤建广, 钱卫平, 赵华. 旋转飞行器分集式测速信号处理方法[J]. 宇航学报, 2010, 31(10):2374-2380. [Feng Jian-guang, Qian Wei-ping, Zhao Hua. Processing of spacecraft diversity Doppler signal under spinning flight[J]. Journal of Astronautics, 2010, 31(10):2374-2380.]

[2]刘嘉兴. 飞行器测控通信工程[M]. 北京：国防工业出版社, 2010:353-380. [Liu Jia-xing. Engineering of spacecraft TT&C technology and communication [M]. Beijing: National Defense Industry Press, 2010: 353-380.]

[3]彭正琴,翟浩,陆防, 等. 基于多参考源的铷原子钟校频方案的设计与实现[J].宇航计测技术, 2013(33):54-57. [Peng Zheng-qin, Zhai Hao, Lu Fang, et al. Design and realization of frequency calibration for Rubidium frequency standard based on multi-reference source [J]. Journal of Astronautic Metrology and Measurement, 2013(33):54-57.]

[4]Allan D. Time and frequency(time-domain) characterization, estimation, and prediction of precision clocks and oscillators[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 1987, 34(6):647-654.

[5]荣文博,单秀旭.频率源振动对测速精度的影响[J].飞行器测控学报, 2015, 34(3):230-233.[Rong Wen-bo，Shan Xiu-xu.Influence of frequency source vibration on velocity measurement accuracy[J].Journal of Spacecraft TT & C Technology, 2015, 34(3)：230-233.]

[6]刘海颖,杨宇晓,丁尚文,等. 地面站频率不稳定对航天器跟踪性能影响的分析[J]. 系统工程与电子技术, 2010, 32(4)：816-819. [Liu Hai-ying, Yang Yu-xiao, Ding Shang-wen, et al. Influence analysis of instable frequency of ground stations on tracking performance of spacecrafts [J]. Systems Engineering and Electronics, 2010, 32(4)：816-819.]

[7]杨俊,许强. 频率源的相位噪声对雷达系统性能的影响[J]. 舰船电子对抗, 2016,39(1):58-61. [Yang Jun, Xu Qiang. Influence of phase noise of frequency source on radar system performance [J]. Shipboard Electronic Countermeasure, 2016,39(1):58-61.]

[8]徐玲.超高稳频率源的设计与应用[J].传感器与微系统, 2009,28(8):92-95. [Xu Ling. Design and application of frequency source with ultra stability [J]. Transducer and Micro-system Technologies, 2009,28(8):92-95.]

[9]王立军. 频率源的平稳切换技术研究[D]. 西安:西安电子科技大学, 2013. [Wang Li-jun. Research of smooth switching technology for frequency source[D].Xi’an: Xidian University, 2013.]

[10]苟向阳. 导航卫星时钟的锁相环技术[D]. 西安:西安电子科技大学, 2013年. [Gou Xiang-yang. Phase-locked loop technology of navigation satellite[D]. Xi’an: Xidian University, 2013.]

[11]成亚勇. 航天测控系统中双向多普勒测速误差分析[J]. 数字技术与应用, 2016(1):255-256.[Cheng Ya-yong.Velocity error aualysis of bistatic Doppler radar in aerospace TT & C[J].Digital Technology & Application,2016(1):225-256.]

[12]刘友永, 郭肃丽, 金松坡. 高精度单向测速系统中电波传播引入的测速误差分析[J]. 飞行器测控学报, 2010, 29(5):20-24. [Liu You-yong, Guo Su-li, Jin Song-po. Analysis of velocity measurement error caused by electromagnetic propagation for high precision one-way velocity measurement systems[J]. Jour-nal of Spacecraft TT & C Technology, 2010, 29(5):20-24.]

[13]樊多盛,施韶华,李孝辉. Kalman滤波的铷原子钟控制算法[J].宇航学报,2015,36(1):90-95. [Fan Duo-sheng, Shi Shao-hua, Li Xiao-hui. An algorithm for the Rubidium atomic clock control based on the Kalman filter [J]. Journal of Astronautics, 2015, 36(1):90-95.]

[14]FEI Inc. Rubidium atomic frequency standard model FE-5650A [EB/OL]. 2007[2017]. http://freqele c.com/rb _osc_fe5650a.html.

[15]Boroditsky R, Gomez J. Testing phase noise of ultra low phase noise OCXO-challenges and solutions[C]. IEEE International Frequency Control Symposium,Baltimore,USA,May 21-24,2012.

[16]Chang W,He Y,Wen L H, et al. A vertical test system for China-ADS project injector Ⅱ superconducting cavities[J]. Chinese Physics C, 2014, 38(5):82-86.

[17]叶玲玲,孙朝斌,沈小青,等. PN9000相位噪声测试系统扩频方法研究[J]. 计算机测量与控制, 2017, 25(5):32-34. [Ye Ling-ling, Sun Chao-bin, Shen Xiao-qing, et al. Research on expanding frequency range method of PN9000 phase noise measurement system[J]. Computer Measurement & Control, 2017, 25(5):32-34. ]

[18]崔书华. 多测速系统最优弹道估计方法及应用[J].弹箭与制导学报, 2012，32(4): 215-218.[Cui Shu-hua. Optimal estimation and application of velocity measurement system[J]. Journal of Projectiles Rockets Missiles and Guidance, 2012, 32(4): 215-218. ]