目标捕获后航天器组合体的角动量转移与抑振规划

王兴龙，周志成，曲广吉

(中国空间技术研究院通信卫星事业部， 北京 100094)

0　引　言

航天器在轨服务[1-2]是我国正在建设发展的重要航天系统工程之一。服务卫星通过空间机械臂在轨捕获失稳目标卫星[3]，是对其进行在轨服务的前提和基础。失稳卫星往往因其残余角速度和扰动等因素而处于慢旋或翻滚状态。目标捕获后，服务卫星和目标卫星在空间机械臂的连接下成为一个组合体。机械臂通过自身关节运动，将两星的相对位置姿态调整至期望值，同时消除两星的相对运动，使其达到相对位姿稳定状态。在此过程中，存在两个较为突出的问题：一方面，组合体处于自由漂浮状态，系统角动量守恒，相对位姿调整与稳定过程中伴随着角动量转移，角动量由目标卫星逐渐转移至整个组合体；另一方面，当服务卫星和目标卫星均为带有太阳翼等柔性附件的大型卫星平台时，机械臂和太阳翼的柔性振动对组合体控制精度影响较大，严重时甚至可能损坏组合体。

以往失稳目标捕获研究多集中在捕获前机械臂的规划控制[4-5]和捕获时末端的接触碰撞[6-7]，对捕获后组合体的角动量转移与抑振规划研究较少。Xu等[8]基于动量守恒提出了空间机械臂动力学耦合问题的混合建模和分析方法。Dimitrov等[9]和刘厚德等[10]分别提出了偏置动量方法和协调控制方法对组合体进行角动量管理与分配，但其所提方法均采用飞轮作为角动量吸收装置，容易饱和，所能转移的角动量有限。柔性组合体振动抑制方面，通过智能优化算法搜索机械臂最优抑振轨迹是一种有效的解决方法。Akira[11]建立了柔性机械臂动力学模型，通过遗传算法得到机械臂振动能量最小的抑振轨迹。Meng等[12]和Xu等[13]建立了考虑太阳翼等柔性附件振动的柔性基座和机械臂耦合动力学模型，并基于此提出了一种振动抑制轨迹规划方法。但以往建模大多只考虑机械臂柔性或太阳翼等附件柔性，没有对机械臂捕获目标后形成的柔性组合体进行动力学建模，也缺少能够综合抑制机械臂和太阳翼等的柔性振动的轨迹规划方面的研究。

本文提出一种航天器组合体角动量转移与振动抑制复合规划方法。建立同时考虑机械臂和太阳翼柔性的组合体动力学模型。设计角动量转移优化方法，并基于粒子群算法规划机械臂最优抑振轨迹。最后通过仿真，检验规划方法的有效性。

1　航天器组合体动力学建模

1.1　系统设定和符号定义

目标捕获后形成的航天器组合体的简化模型如图1所示。服务卫星和目标卫星均设定为带有太阳翼等柔性附件的大型卫星平台。目标卫星处于无控失稳状态，绕自身最大惯量轴慢旋。空间机械臂根部固定于服务卫星，末端与目标卫星固连并跟随目标卫星作旋转运动。服务卫星捕获目标前姿态稳定，捕获目标后关闭姿轨控系统，整个组合体处于自由漂浮状态，系统动量守恒。

图1　航天器组合体简化模型Fig.1　Simplified model of spacecraft combination

机械臂臂杆和卫星太阳翼均视为柔性体，柔性变形视为小变形。本文的规划对象为机械臂关节输出角度，因此机械臂关节可视为黑箱模型，不对关节内部结构进行建模，不考虑关节柔性。组合体动力学建模所用坐标系和基本符号定义如下：

n：空间机械臂自由度

ns,nt：服务卫星和目标卫星太阳翼的数量

ΣI,Σmi：惯性坐标系、臂杆i固连坐标系

OI,Og：惯性系ΣI原点、组合体系统质心

Om0,Ome：服务卫星质心、目标卫星质心

Omi：机械臂关节i中心点

Osi,Oti：服务卫星和目标卫星太阳翼的链接点

rm0：从OI到Om0的位置矢量

lmi：从Omi到Omi+1的位置矢量

bm0,bsi：从Om0分别到Om1,Osi的位置矢量

bti：从Omn到Oti的位置矢量

rmi,h,rsi,h,rti,h：从OI分别到臂杆i、服务卫星太阳翼i和目标卫星太阳翼i上任意点h的位置矢量

ami,h,asi,h,ati,h：从Omi到臂杆i、从Osi到服务卫星太阳翼i、从Oti到目标卫星太阳翼i上任意点h的位置矢量

δmi,h,δsi,h,δti,h：臂杆i、服务卫星太阳翼i、目标卫星太阳翼i上任意点h的柔性变形矢量

δmi,l：臂杆i末端的柔性变形矢量

vm0,ωm0：服务卫星的速度和角速度矢量

ωmi：机械臂臂杆i的角速度矢量

zmi：机械臂关节i旋转方向的单位矢量

θmi：机械臂关节i输出的关节角度

mjAmi：从Σmi系到Σmj系的姿态转换矩阵

E：单位矩阵

1.2　柔性组合体动力学模型

(1)

(2)

(3)

(4)

采用假设模态法对柔性体进行离散化描述，柔性变形量δmi,l,δmi,h,δsi,h,δti,h按正则模态展开，有

(5)

式中：Φmi,Φsi,Φti分别为机械臂臂杆i、服务卫星太阳翼i、目标卫星太阳翼i的正则模态矩阵，ηmi,ηsi,ηti分别为机械臂臂杆i、服务卫星太阳翼i、目标卫星太阳翼i的模态坐标。

组合体的动能T为服务卫星、目标卫星和空间机械臂的动能之和，将式(1)～式(5)代入组合体动能表达式，整理得到

(6)

(7)

(8)

(9)

M(q)为组合体的广义惯量矩阵：

(10)

式中：Mvv为组合体总质量，Iωω为组合体相对其系统质心的转动惯量，Rvω为服务卫星转动对自身平动的刚性耦合系数，Rvθ,Rωθ,Rθθ为机械臂关节转动分别对服务卫星平动、服务卫星转动和自身转动的刚性耦合系数，Fvη,Fωη,Fθη为机械臂臂杆和卫星太阳翼振动分别对服务卫星平动、服务卫星转动和机械臂关节转动的柔性耦合系数[14]。

目标捕获后，服务卫星姿轨控系统关闭，整个组合体不受外力作用，满足线动量和角动量守恒。假设组合体初始线动量和角动量分别为P0,L0，将式(1)～式(5)代入组合体动量表达式，整理得到

(11)

式中：Hs,Hm,Hf为系数矩阵，且Hs非奇异。

(12)

式中：

(13)

将式(12)代入式(6)，组合体动能T可重写为

(14)

式中：

M(Θm,η)=A(Θm,η)TM(q)A(Θm,η)N(Θm,η)=B(Θm,η)TM(q)B(Θm,η)

(15)

组合体的势能V为服务卫星和目标卫星太阳翼以及机械臂臂杆柔性变形势能之和，其表达式为

(16)

式中：Λf为机械臂和太阳翼的广义刚度矩阵。

将式(14)和式(16)代入第二类拉格朗日方程，整理得到柔性组合体的动力学方程为

(17)

式中：C(Θm,η)为包括离心力和哥氏力在内的非线性力项，D(Θm,η)为组合体初始运动对应的力项，Tm为机械臂关节驱动力矩。

2　角动量转移优化方法

失稳目标捕获后，组合体位姿调整与稳定的主要难点在于如何吸收目标卫星的角动量。飞轮作为角动量吸收装置简单易行，但容易饱和，所能吸收的角动量有限；推力器喷气又会对机械臂运动产生干扰，降低机械臂控制精度。因此，本文采用先相对稳定再绝对稳定的控制方案：目标捕获后，先关闭服务卫星姿轨控系统，通过机械臂关节运动调整两星相对位姿，消除其相对运动，将目标卫星的角动量转移至整个组合体；待实现两星相对稳定后，再重新开启服务卫星姿轨控系统，消除组合体的旋转，实现组合体在惯性空间的姿态稳定。

对于具有冗余自由度(n≥7)的空间机械臂，存在多种构型满足两星相对稳定后的相对期望位姿要求。因此，可通过优化方法，规划得到机械臂最优构型，使组合体相对位姿稳定后的角速度最小，便于地面对组合体的跟踪控制。

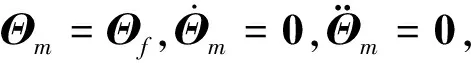
(18)

设m0rme为目标卫星质心Ome到服务卫星质心Om0的相对期望位置在Σm0系中的坐标分量，m0Amn为目标卫星到服务卫星的相对期望姿态转换矩阵，则角动量转移优化的等式约束可整理为

(19)

式中：m0bm0为bm0在Σm0系中的坐标分量，milmi为lmi在Σmi系中的坐标分量。

(20)

式中：Hpv,Hpω,Hlv,Hlω为Hs的分块矩阵。令

(21)

可证明If非奇异，则目标函数可取为

(22)

3　基于粒子群算法的抑振轨迹规划

3.1　关节运动参数化

目标捕获后，航天器组合体呈两头重中间轻的“哑铃”状构型，该种构型使得处于连接位置的空间机械臂的基频显著降低。同时，服务卫星和目标卫星的太阳翼本身也是基频很低的大型柔性结构。机械臂运动过程中容易激起自身和太阳翼的柔性振动，对其控制精度产生影响。因此，组合体位姿调整与稳定过程中需考虑抑制相关柔性振动，通过智能优化算法规划机械臂的最优抑振轨迹。

设组合体位姿调整与稳定过程的起止时刻分别为t0,tf。在起始时刻t0=0，机械臂关节的初始运动状态为

(23)

在终止时刻tf，由角动量转移优化可得机械臂关节的最终运动状态为

(24)

采用七次多项式对关节运动轨迹进行参数化：

θmi(t)=ai7t7+ai6t6+ai5t5+ai4t4+ai3t3+ai2t2+ai1t+ai0

(25)

式中：ai0,ai1,…,ai7为七次多项式系数。将边界条件式(23)和式(24)代入得

(26)

参数化后的每个关节运动轨迹θmi(t)仅包含两个待定参数ai6,ai7，则抑振轨迹规划的优化参数可取为

(27)

3.2　目标函数定义

模态坐标η能够直观反映机械臂和太阳翼的柔性振动，因此抑振轨迹规划的目标函数可定义为

(28)

式中：Q为机械臂和太阳翼的柔性振动能量，右边第一项为机械臂运动过程中的柔性振动能量，第二项为机械臂运动结束后的残余振动能量，λ1,λ2分别为各自的权重系数。抑振轨迹规划问题转化为求一组最优参数a=[a16a17a26a27…an6an7]，使目标函数Q取最小值，进而得到机械臂的最优抑振轨迹Θm(t)。

3.3　粒子群优化算法求解

粒子群优化算法(Particle Swarm Optimization, PSO)由Kennedy和Eberhart于1995年首次提出[16]，是一种基于群体智能的优化算法，通过一组初始化的群体在搜索空间中并行搜索，具有实现简单、收敛快、精度高等优点，可用于求解本文的抑振轨迹规划问题。

粒子群算法具体求解步骤如下：

(1)设粒子种群数量为M，在N维搜索空间中(N=2n)，随机初始化每个粒子i的位置Xi和速度Vi，其中Xi为

(29)

将Xi代入式(26)和式(25)计算机械臂关节运动轨迹Θm(t)，再代入组合体动力学方程式(17)求解模态坐标η(t)，最后代入式(28)计算目标函数Q。设Pi为粒子i的个体最优位置，其初值为

Pi(0)=Xi(0)

(30)

设Pg为全局最优位置，其初值为

Pg(0)={Pi(0)|Q(Pi)=min{Q(P1),…,Q(PM)}}

(31)

(2)假设第k代的Xi(k),Vi(k),Pi(k),Pg(k)已知，则第k+1代的粒子位置Xi(k+1)和速度Vi(k+1)按下式规划：

Vi(k+1)=wVi(k)+c1ri1[Pi(k)-Xi(k)]+

c2ri2[Pg(k)-Xi(k)]

(32)

Xi(k+1)=Xi(k)+Vi(k+1)

(33)

式中：w为惯性权重，c1,c2为学习因子，ri1,ri2为[0,1]区间内的随机数。

(3)更新粒子i的个体最优位置Pi(k+1)：

(34)

(4)更新全局最优位置Pg(k+1)：

(35)

(5)设最大迭代次数为kmax，期望目标函数值为Qd。若k≥kmax或Q(Pg(k))≤Qd，则判定满足算法终止条件，结束迭代，否则k=k+1，转步骤(2)。

4　仿真校验

4.1　工程算例

通过工程算例在MATLAB和ADAMS联合仿真平台上进行仿真，校验本文规划方法的有效性。服务卫星和目标卫星设定采用成熟型号卫星平台。机械臂设定为空间7自由度机械臂，整体构型与国际空间站遥控机械臂系统相似，采用传统DH建模方法描述，如图2所示，D-H参数如表1所示。组合体动力学参数如表2所示。机械臂臂杆和卫星太阳翼的材料参数如表3所示。

图2　空间7自由度机械臂D-H坐标系Fig.2　D-H frames of 7-dof space manipulator

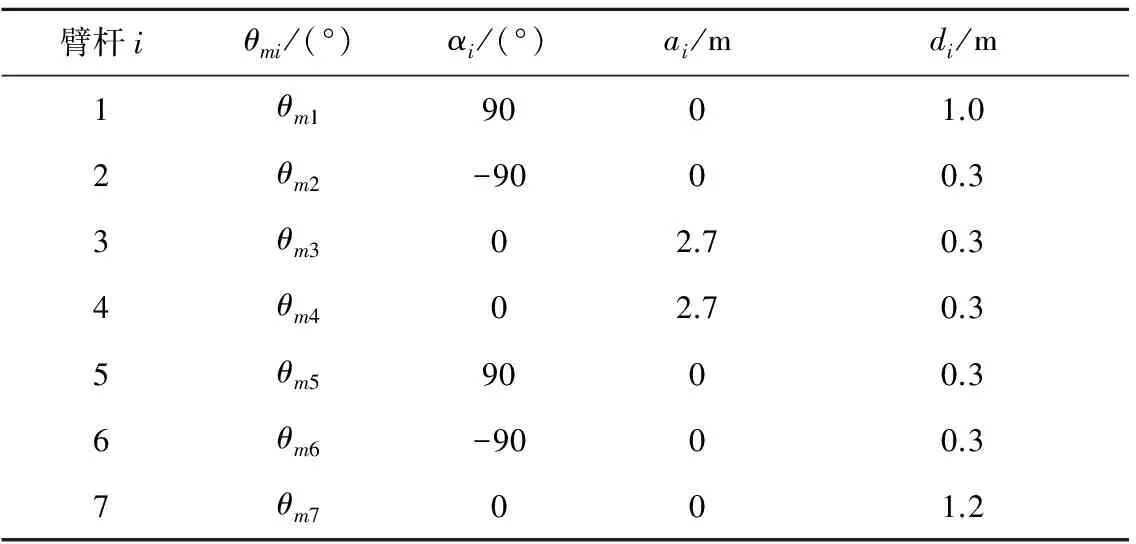
臂杆iθmi/(°)αi/(°)ai/mdi/m1θm19001．02θm2-9000．33θm302．70．34θm402．70．35θm59000．36θm6-9000．37θm7001．2

表2　航天器组合体动力学参数Table 2　Dynamic parameters of spacecraft combination

表3　柔性部件材料参数Table 3　Material parameters of flexible components

4.2　仿真结果

图3　角动量转移优化目标函数Fig.3　Objective function of angular momentum transfer optimization

采用粒子群算法进行抑振轨迹规划仿真，目标函数Q随迭代次数k的变化曲线如图4所示。

图4　抑振轨迹规划目标函数Fig.4　Objective function of vibration suppression trajectory planning

从图中可以看出，随着k增加，Q单调递减。当迭代至k=28时，Q取极小值2.652 kg·m2，且在后续迭代过程中保持不变，因此该值可作为抑振轨迹规划的最优目标函数值。

仿真得到的空间机械臂关节最优抑振轨迹Θm(t)与常规五次多项式轨迹进行对比，结果如图5所示。机械臂臂杆3、服务卫星太阳翼1和目标卫星太阳翼1的一阶模态坐标ηm3,ηs1,ηt1的对比结果分别如图6～图8所示。

图5　空间机械臂关节角度Fig.5　Joint angles of space manipulator

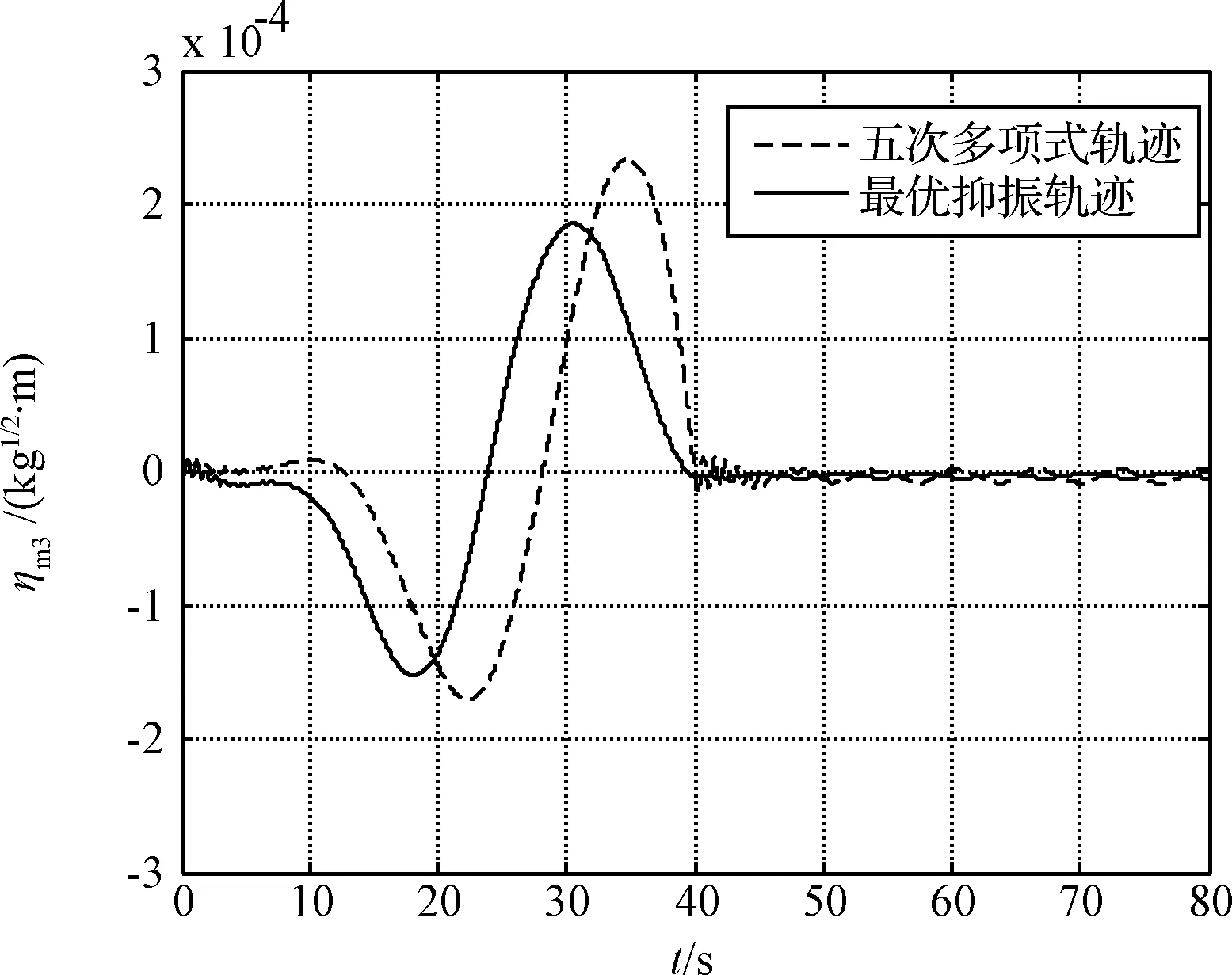
图6　空间机械臂臂杆一阶模态坐标Fig.6　First modal coordinate of space manipulator link

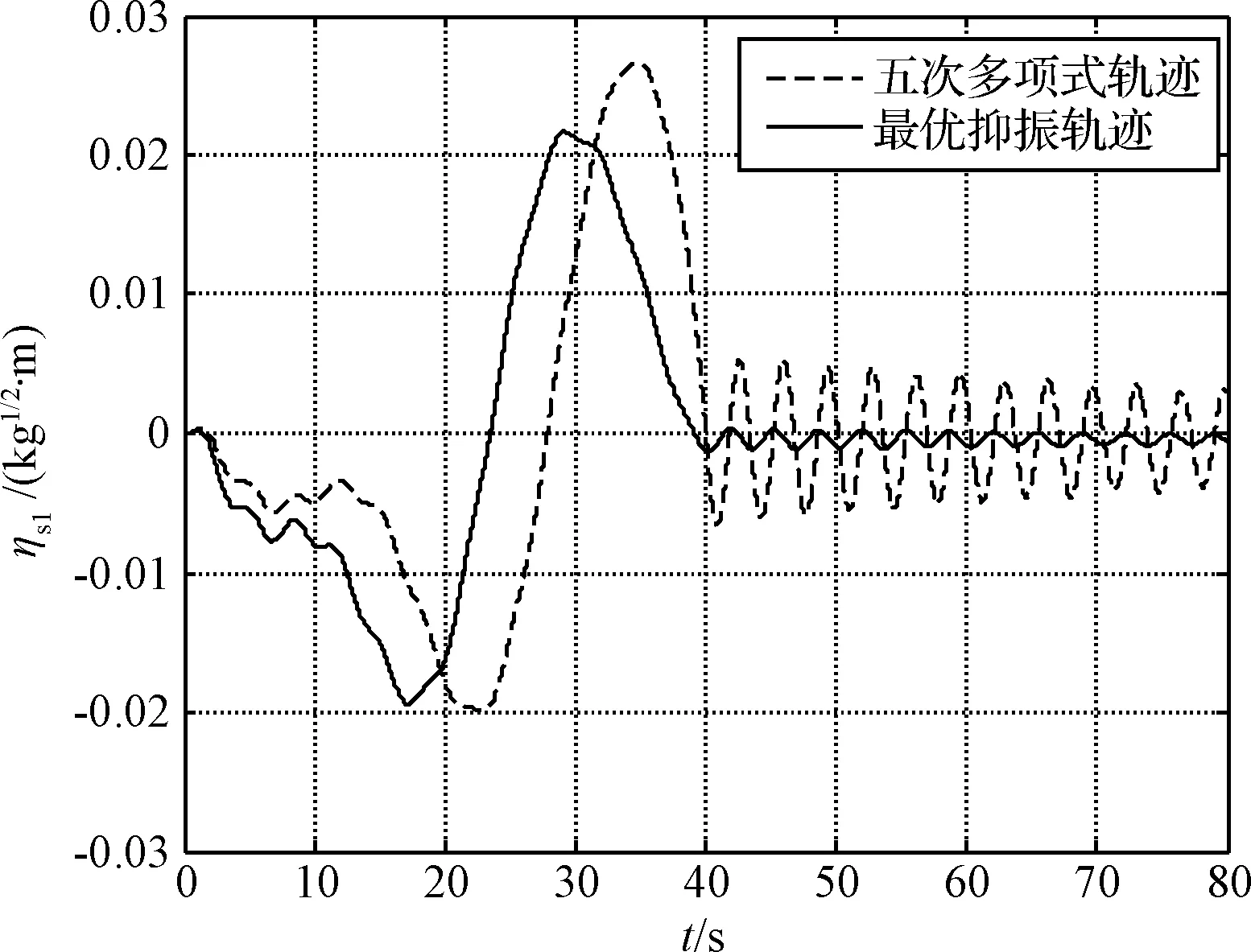
图7　服务卫星太阳翼一阶模态坐标Fig.7　First modal coordinate of servicing satellite solar array

图8　目标卫星太阳翼一阶模态坐标Fig.8　First modal coordinate of target satellite solar array

从图中可以看出，当机械臂关节沿最优抑振轨迹运动时，机械臂和太阳翼的残余振动与五次多项式轨迹相比均大幅减少，振动幅值减少约80%，表明其柔性振动得到有效抑制，从而证明本文提出的抑振轨迹规划方法是有效可行的。

5　结　论

本文针对失稳目标捕获后航天器组合体位姿调整与稳定问题，提出了一种角动量转移与振动抑制复合规划方法，并通过数值仿真验证了方法的有效性和适用性。方法具有以下特点：1)有效实现组合体的角动量转移，并保证组合体相对位姿稳定后的角速度最小；2)显著降低机械臂和太阳翼等柔性部件的振动，从而提高组合体的相对位姿控制精度。

由于方法的规划对象为机械臂关节输出角度，未对关节内部结构进行建模，因此无法抑制关节的柔性振动。关节振动抑制问题可在后续工作柔性机械臂控制系统设计时进一步加以解决。

[1]周志成, 曲广吉. 通信卫星总体设计和动力学分析[M]. 北京：中国科学技术出版社, 2012.

[2]梁斌, 徐文福, 李成, 等. 地球静止轨道在轨服务技术研究现状与发展趋势[J]. 宇航学报. 2010, 31(1): 1-13. [Liang Bin, Xu Wen-fu, Li Cheng, et al. The status and prospect of orbital servicing in the geostationary orbit [J]. Journal of Astronautics, 2010, 31(1): 1-13.]

[3]王兴龙, 周志成, 曲广吉. 空间机械臂捕获失稳目标的动态轨迹规划方法[J]. 宇航学报. 2017, 38(7): 678-685. [Wang Xing-long, Zhou Zhi-cheng, Qu Guang-ji. Dynamic trajectory planning method of space manipulator for capturing a tumbling target [J]. Journal of Astronautics, 2017, 38(7): 678-685.]

[4]Aghili F. Optimal control of a space manipulator for detumbling of a target satellite [C]. International Conference on Robotics and Automation, Kobe, Japan, May 12-17, 2009.

[5]徐拴锋, 杨保华, 张笃周, 等. 面向非合作目标抓捕的机械臂轨迹规划方法[J]. 中国空间科学技术. 2014, 8(4): 8-15. [Xu Shuan-feng, Yang Bao-hua, Zhang Du-zhou, et al. Trajectory planning algorithm for manipulators capturing non-cooperative objects [J]. Chinese Space Science and Technology, 2014, 8(4): 8-15.]

[6]Stolfi A, Gasbarri P, Sabatini M. Impedance control of a multi-arm space robot for capturing a non-cooperative target [C]. International Astronautical Congress, Guadalajara, Mexico, Sept 26-30, 2016.

[7]郭闻昊, 王天舒. 空间机器人抓捕目标星碰撞前构型优化[J]. 宇航学报. 2015, 36(4): 390-396. [Guo Wen-hao, Wang Tian-shu. Pre-impact configuration optimization for a space robot capturing target satellite [J]. Journal of Astronautics, 2015, 36(4): 390-396.]

[8]Xu W F, Peng J Q, Liang B, et al. Hybrid modeling and analysis method for dynamic coupling of space robots[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(1): 85-98.

[9]Dimitrov D, Yoshida K. Utilization of the bias momentum approach for capturing a tumbling satellite [C]. International Conference on Intelligent Robots and Systems, Sendai, Japan, Sept 28-Oct 2, 2004.

[10]刘厚德, 梁斌, 李成, 等. 航天器抓捕后复合体系统稳定的协调控制研究[J]. 宇航学报. 2012, 33(7): 920-929. [Liu Hou-de, Liang bin, Li cheng, et al. Research on coordinated control method for stabilizing a coupling system after the spacecraft is captured [J]. Journal of Astronautics, 2012, 33(7): 920-929.]

[11]Akira A. Trajectory planning for residual vibration suppression of a two-link rigid-flexible manipulator considering large deformation [J]. Mechanism and Machine Theory, 2009, 44(9): 1627-1639.

[12]Meng D S, Wang X Q, Xu W F, et al. Space robots with flexible appendages: dynamic modeling, coupling measurement, and vibration suppression [J]. Journal of Sound and Vibration, 2017, 396: 30-50.

[13]Xu W F, Meng D S, Chen Y Q, et al. Dynamics modeling and analysis of a flexible-base space robot for capturing large flexible spacecraft [J]. Multibody System Dynamics, 2014, 32(3): 357-401.

[14]Wang X L, Zhou Z C, Qu G J. Dynamics modeling of flexible spacecraft combination connected by a space manipulator [C]. International Astronautical Congress, Adelaide, Australia, Sept 25-29, 2017.

[15]龚纯, 王正林. 精通MATLAB最优化计算(第2版)[M]. 北京：电子工业出版社, 2012.

[16]Eberhart R, Kennedy J. A new optimizer using particle swarm theory [C]. International Symposium on Micro Machine and Human Science, Nagoya, Japan, Oct 4-6, 1995.