带有引诱角色的有限时间协同制导方法

张　帅，郭　杨，王仕成

(火箭军工程大学精确制导与仿真实验室， 西安 710025)

0　引　言

随着导弹防御系统网络化、信息化、精准化程度越来越高，我方高价值飞行器如何有效突破对方武器系统的拦截已成为制导领域关注的热点课题。针对上述问题，考虑一种协同突防方案：高价值飞行器(突防器)自身携带一枚防御导弹(防御器)，突防器作为引诱角色，防御器作为拦截角色，两个飞行器协同配合以应对来袭的拦截器。显然，相比于传统的单一突防方式，突防器配合防御器进行引诱机动的协同制导方案能够增大反拦截的成功率，更有利于突防器的成功突防。可见，研究上述三体协同制导问题对保护我方高价值飞行器具有十分重要的现实意义[1-2]。

Boyell在文献[3-4]中最早提出三体协同制导思路，并初步探索了三体协同方案。近些年来，文献[5-6]基于三体制导背景，提出了一种视线制导律。该制导律基于一种比较简单的三角几何接近原理，能够保证防御器在向拦截器制导过程中始终处于突防器和拦截器视线连线上，从而保证了在相互接近的过程中防御器能成功拦截拦截器。文献[7]在假设拦截器分别采用比例导引律、修正比例导引律和最优制导律的情况下，基于最优控制理论推导了突防器和防御器最优合作突防策略。在文献[7]的基础上，文献[8]将拦截器动力学特性扩展至任意阶，并基于线性二次型方程提出了三种制导方法，最后通过数学仿真，校验了突防器机动配合防御器的协同制导方案是最有效的。文献[9]针对攻防双方，基于最优控制理论分别提出了两种制导方案：首先从最大逃逸脱靶量需求出发，为拦截方设计了组合制导算法以实现对突防器的有效拦截以及对防御器的机动规避；其次从最小拦截脱靶量的需求出发，为突防方设计了合作制导方案以实现反拦截。文献[10]采用零效脱靶量作为滑模切换面，基于滑模控制理论提出了一种非线性合作突防方案，该方案能够保证在前置角估计误差较大的情况下仍具有较好的制导精度。

在设计协同制导律时，不仅要充分考虑制导律的收敛特性，还要考虑制导律的收敛时间问题。在飞行器制导领域，有限时间收敛的制导律受到广泛关注：文献[11]针对一打一问题，基于有限时间理论提出了一种抗饱和制导律，该制导律能够保证在加速度不超过物理限制的情况下有较好的拦截精度。文献[12]基于有限时间H2范数性能指标提出了一种脱靶量/能量最优导弹机动突防策略。文献[13]针对高速机动目标，基于滑模自适应理论提出了一种三维有限时间收敛的制导律。文献[14]针对机动目标，基于有限时间Lyapunov稳定理论提出了一种连续有限时间制导律。由此可见，在有限时间框架下研究协同制导问题十分必要[15-16]。而目前主要有两种有限时间概念：一种是Bhat和Bernstein在文献[17]中提出的有限时间收敛概念，该有限时间理论主要指在Lyapunov稳定的前提下，系统状态在一个相对有限的时间区间(而不是无限时间)内收敛到平衡点；另一种是Amato等[18]提出的有限时间概念，主要是指系统输入在范数有界的情况下，系统状态或者输出在给定的时间内亦范数有界。由于后者关注系统状态在确切的时间段内的收敛特性，且在输入和状态有界的情况下能更好地刻画系统动态品质，因此本文主要关注由Amato等[18]提出的有限时间理论。

从公开发表的成果来看，目前国内对多飞行器协同制导的研究多数集中在拦截时间一致性、不同拓扑结构(如“领弹-从弹”)等多弹协同制导方面[19-23]，对不同角色的三体协同问题的研究还不够系统和深入。上述关于三体制导的研究也大多基于线性二次型和最优控制理论，这些方法在解决最优合作机动问题上具有较好的控制效果，但不能很好地解决制导律有限时间收敛问题。且现有的三体协同制导方法多数是基于突防器、防御器和拦截器三点共线的协同思路，在三点共线的情况下突防方对拦截器的协同探测和协同状态估计误差会大大增加，这不利于突防方对拦截器飞行状态和参数的准确预测，因此本文考虑了带有拦截角约束的协同突防方案，而该协同方案可以很好地克服三点共线带来的弊端。

综上，本文针对多飞行器合作突防问题，在有限时间框架下提出了一种带有拦截角约束的协同制导方法，以微分线性矩阵不等式形式给出了有限时间协同制导律设计方法，并在理论上进行了相关的证明。在突防器进行引诱配合的情况下，该方法能够确保防御器在有限时间内以预置的拦截角拦截拦截器。同时，在不同拦截角和初始发射条件下，该方法也能有较好的稳定性。

1　问题描述

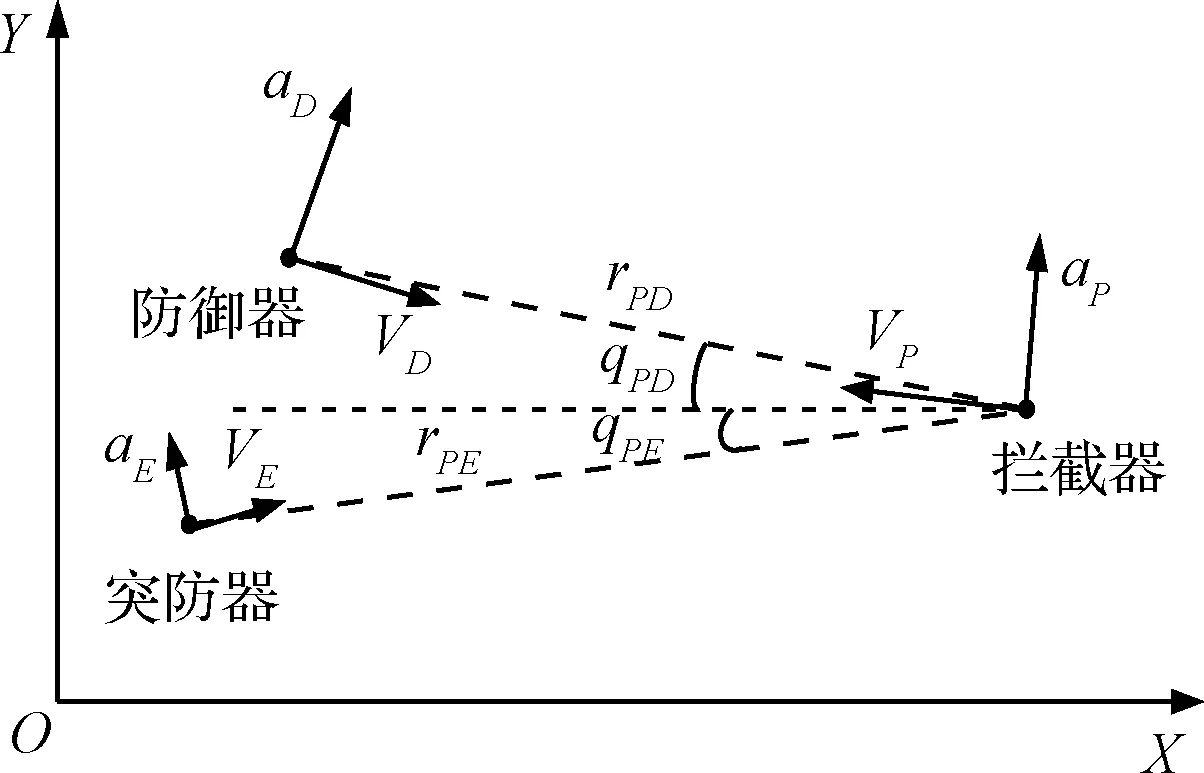
图1　三体协同制导作战示意图Fig.1　Schematic diagram of the three-aircraft cooperative guidance

1.1　动力学与运动学

根据惯性坐标系和视线坐标系之间的转化关系，忽略视线角变化率二阶小量，可以得到突防器与拦截器之间二维相对运动学方程：

(1)

同理，可以得到防御器与拦截器之间相对运动学方程：

(2)

突防器与拦截器之间的拦截结束时间可近似为：

(3)

类似地，防御器与拦截器之间的拦截结束时间可近似为：

(4)

式中：rPE(0)和rPD(0)表示初始相对距离，VPE和VPD表示接近速度。由于防御器是从突防器上发射的，因此初始相对距离rPE(0)与rPD(0)相等。而防御器在速度和机动能力上均比突防器有优势，认为VPD>VPE，因此tfPE>tfPD，这是高价值飞行器能够成功突防的必要条件之一。

用tgPE和tgPD表示剩余飞行时间，则相对距离可表示为：

(5)

假设三个飞行器动力学特性可等效为一阶惯性环节：

(6)

式中：τ为过载响应时间，ac为飞行器控制指令。据此可得飞行控制系统时域描述为：

(7)

1.2　突防器不配合防御器进行引诱机动

(8)

y(t)=C(t)x(t)

(9)

式中：u(t)为控制输入，包含需要设计的突防方协同制导指令aEC和aDC;w(t)为外部干扰输入；G(t)为相应的干扰传递矩阵；y(t)为系统评价输出；C(t)为相应的输出矩阵。

在本文三体制导背景下，拦截器总是以突防器作为制导目标进行有规律的机动。突防方虽然不能准确得知拦截器所采用制导律的具体表达形式，但是现代制导律本质上可以看作是比例导引加修正项的形式[7,9,16]，所以总能用比例导引律加修正项来近似表示拦截器所采用的拦截制导律。对于不同的制导律形式，只是导引系数N和K存在一定范围的变化。因此，在对协同制导律进行方法研究时，在修正比例制导律情况下得到的研究结果对其它制导律也具有适用性。

A(t)=

1.3　突防器配合防御器进行引诱机动

其余变量和系统输出矩阵与第1.2节相同。控制输入向量u(t)同时包含突防器和防御器的加速度指令信息，通过设计合适的控制器u(t)即可有效地解算协同制导律。

1.4　带有拦截角度约束的协同反拦截模型

(10)

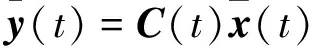
(11)

通过修正系统状态变量，可将拦截角约束条件附加在系统状态变量中，建立带有拦截角度约束的协同反拦截模型。

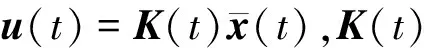
(12)

(13)

注1. 相比于一般的制导方法所采用的时不变反馈参数，这里采用的状态反馈法包含了更为丰富的状态变量信息，在时变的状态反馈矩阵K(t)的作用下，解算出的控制器u(t)也包含了更加全面的状态信息。

2　有限时间协同制导律设计

由于协同制导过程是典型的有限时间过程，各飞行器需在有限时间内完成机动目标，且所建立的系统模型也是在有限时间内才有意义。因此本节采用有限时间控制理论来设计和解算控制器。

2.1　有限时间输入输出稳定理论

定义1[18].对于线性时变系统(14)和(15)，假设系统初始状态x(0)=0，那么

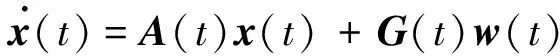
(14)

y(t)=C(t)x(t)

(15)

如果系统对于∀t∈[0,T]满足式(16)，则

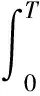
(16)

则称此系统关于(T,Sw,Sy(t))有限时间输入输出稳定。其中，w(t)为外部干扰输入，y(t)为系统的评价输出，[0,T]为有限时间区间，Sw和Sy(t)为预先给定的度量矩阵与度量矩阵函数。

注2.有限时间输入输出稳定与李雅普诺夫BIBO稳定是两个不同的概念。前者关注系统在给定的有限时间段内输入输出的动态特性。而后者主要关注系统在无限时间内输入输出信号上界的存在性。

注3.系统有限时间输入输出稳定特性与有限时间区间[0,T]和度量矩阵Sw,Sy(t)密切相关，系统有限时间输入输出稳定不是独立的概念。当这几个参量变化时，系统可能在此情况下不满足输入输出稳定，此时需要寻找合适的状态反馈控制器使系统满足输入输出有限时间稳定。

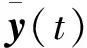
引理1.(有限时间输入输出稳定充分条件)[24]：线性时变系统和关于(T,Sw,Sy(t))有限时间输入输出稳定的一个充分条件是：在有限时间区间[0,T]上，存在一个对称正定的矩阵函数P(t)∈Rn×n，使得以下不等式同时成立：

(17)

P(t)≥CT(t)Sy(t)C(t)对于∀t∈[0,T]

(18)

2.2　协同制导律设计

对于系统(10)和(11)，为有效解算状态反馈控制器u(t)，使系统满足输入输出有限时间稳定，这里以定理的形式给出状态反馈控制器设计方法。

定理1(状态反馈控制器设计方法). 线性时变系统(10)与(11)关于(T,Sw,Sy(t))有限时间输入输出稳定的一个充分条件是：在有限时间区间[0,T]上，存在对称正定的矩阵函数X(t)∈Rn×n和L(t)∈Rr×n，使得微分线性矩阵不等式(19)和(20)成立。

(19)

X(t)≤S-1(t)且S(t)=CT(t)Sy(t)C(t)

(20)

证. 令V(x(t))=xT(t)P(t)x(t)，则有

(21)

根据式(17)和式(21)可得：

(22)

(23)

根据式(22)和式(23)，可推得：

(24)

对式(24)积分可得：

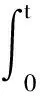
(25)

根据式(15)、(18)和(25)，对于∀t∈[0,T],下式成立：

yT(t)Sy(t)y(t)=xT(t)CT(t)Sy(t)C(t)x(t)<

xT(t)P(t)x(t)<1

(26)

根据式(17)和式(26)，由矩阵的Schur补性质[25]可知下式成立。

(27)

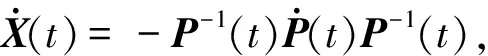
(28)

根据式(18)，经过简单矩阵逆变换可以推得式(20)。进而根据引理1可知状态反馈控制器K(t)=L(t)X-1(t)能保证由式(10)与(11)构成的闭环系统关于(T,Sw,Sy(t))有限时间输入输出稳定。定理得证。

求解状态控制器u(t)，需要求解式(19)所示的微分线性矩阵不等式，可将微分线性矩阵不等式离散化为若干标准的矩阵不等式进行求解[25]。

3　仿真分析

为检验所提出的带有拦截角约束的有限时间协同制导方法，本节开展数学仿真研究。首先根据第1.2节和第1.3节建立的系统模型以及定理1控制器设计方法，解算突防器配合与不配合两种情况下的制导律u(t)；而后将协同制导律带回系统(12)和(13)，开展闭环仿真校验。

3.1　突防器不配合防御器进行引诱机动

为检验第1.2节系统模型和第2.2节所提有限时间制导律设计方法的有效性，在突防器不配合防御器进行引诱机动的情况下，防御器分别采用本文提出的有限时间制导律设计方法(IO-FTS)和文献[22]中式(15)提出的带有拦截角约束的修正比例导引律(APN)，预置拦截角均设置为-15°，开展二维平面仿真研究。仿真参数如表1所示，仿真结果如图2～5所示。

表1　协同制导仿真参数Table 1　Simulation parameters of cooperative guidance

由图2可知，采用上述两种方法时，突防器按照预定的任务水平飞行，不进行配合机动，在0时刻发射防御器以应对来袭的拦截器。拦截器向高价值突防器制导，试图拦截突防器。在突防器不配合防御器进行引诱机动的情况下，防御器在 (6338.6 m,342.4 m) 坐标点成功拦截到拦截器。图3所示为防御器采用两种制导律情况下加速度需求变化曲线。由图2和图3可知，在相同的拦截角约束条件下，防御器采用本文所提的有限时间制导律时，机动轨迹较APN制导律更加平缓，这样可以有效减小防御器的最大需用机动过载，图3所示加速度需求也验证了图2所示轨迹曲线。由此表明本文所提有限时间制导律较APN制导律具有较好的优势。

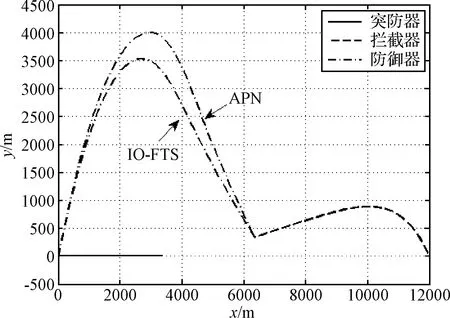
图2　三个飞行器飞行弹道曲线Fig.2　Flight trajectory curves of the three aircraft

图3　防御器加速度实时变化曲线Fig.3　Acceleration variation of defender

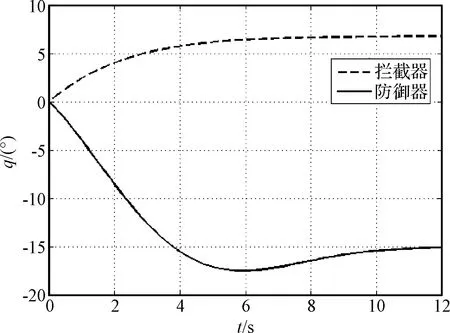
图4　拦截角变化曲线Fig.4　Intercept angle curves

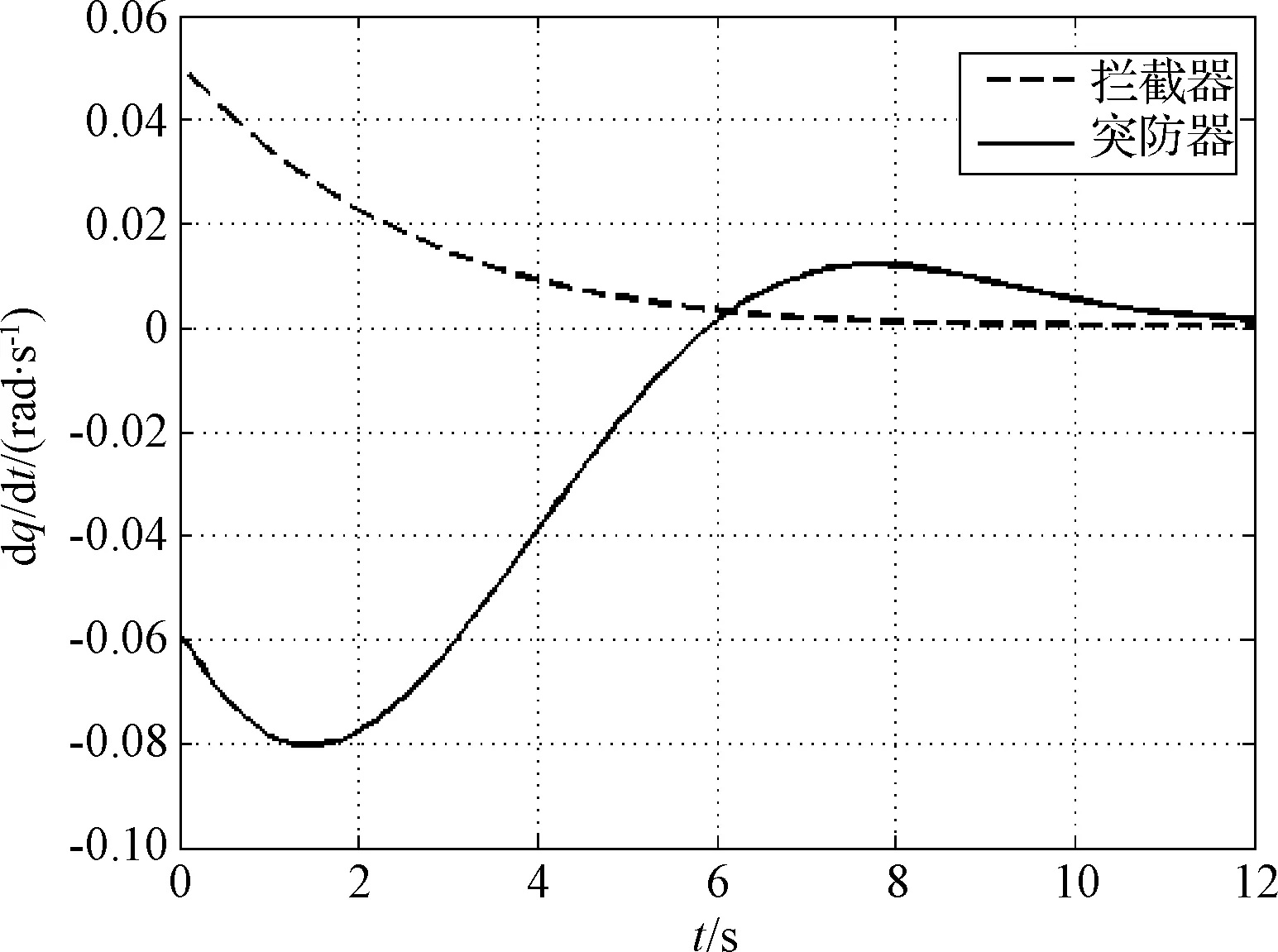
图5　视线角速率变化曲线Fig.5　LOS angle rotation rate

可知，基于有限时间理论的制导律设计方法能够取得预置的拦截效果，较APN制导律有更好的效果。

3.2　突防器配合防御器进行引诱机动

在突防导弹配合防御器机动的情况下，根据第1.3节协同反拦截模型和定理1设计协同制导律。防御器预置拦截角取为-15°，其余仿真条件与表1相同。仿真结果如图6～8所示。

由图6可知，在协同防御的过程中，突防器进行引诱机动以配合防御器进行协同反拦截。对比图2和图6，在协同制导指令的作用下，突防器与防御器之间存在明显的配合，能够较好地实现合作反拦截目标。仿真结果校验了本文所提协同制导方法的有效性。

图6　三个飞行器飞行弹道曲线Fig.6　Flight trajectory curves of the three aircraft

图7　防御器加速度实时变化曲线Fig.7　Acceleration variation of defender

图8　突防器加速度实时变化曲线Fig.8　Acceleration variation of evader

图7和图8所示为防御器和突防器在突防器配合与不配合情况下加速度变化曲线。在这两种情况下，防御器最大需用加速度分别为149.3 m/s2和276.5 m/s2。由图8可知，在协同突防的情况下，突防器进行了一定的引诱机动。

由以上仿真结果可知，在突防器机动配合的情况下，防御器能够较大幅度地节省最大需用加速度，而突防器进行的配合机动只消耗了较小的加速度，可以看成突防器帮助防御器“分担”了部分机动的需求。在实际反拦截过程中，各个飞行器的物理机动过载一般是有限的，而本文提出的协同突防制导方案能够以突防器较小的机动需求为代价实现防御器较大的机动才能达到的效果，表明了本文协同突防方案较单一突防具有较大的优势。

3.3　不同拦截角对制导律性能的影响

为评估协同制导律对不同预置拦截角条件下的控制效果，在突防器配合防御器进行引诱机动的情况下，分别设置拦截角为-10°，-15°，-20°，-25°，-30°，开展仿真研究。其他仿真参数与表1相同，仿真结果如图9～10所示。

图9　防御器拦截角变化曲线Fig.9　Intercept angle curves of defender

由图9～10和表2所示防御器防御效果可知，在不同的预置拦截角情况下，拦截角在有限时间内最终都能够收敛到预定的角度附近，视线角速率均能收敛到0附近，且防御器具有较小的脱靶量。仿真结果表明本文所设计的协同制导律能够适应不同的拦截角度需求，对预置拦截角的变化有较强的稳定性。

图10　防御器视线角速率变化曲线Fig.10　LOS angle rotation ratecurves of defender

预置拦截角终端拦截角脱靶量/m-10°-10．06°0．35-15°-15．11°0．46-20°-20．09°0．74-25°-25．13°0．65-30°-30．11°0．76

3.4　不同初始发射条件对协同制导律的影响

面对复杂的战场环境和不同的作战需求，防御器初始发射状态可能在不断变化。因此，研究初始发射条件对协同制导效果的影响显得十分必要。在突防器配合防御器进行引诱机动的情况下，拦截角设置为-15°，初始发射状态设置为5种情况，如表3所示，其余参数与表1相同。

表3　不同初始发射状态仿真参数设置Table 3　Simulation parameters under different initial launch conditions

图11　防御器拦截角变化曲线Fig.11　Intercept angle curves of defender

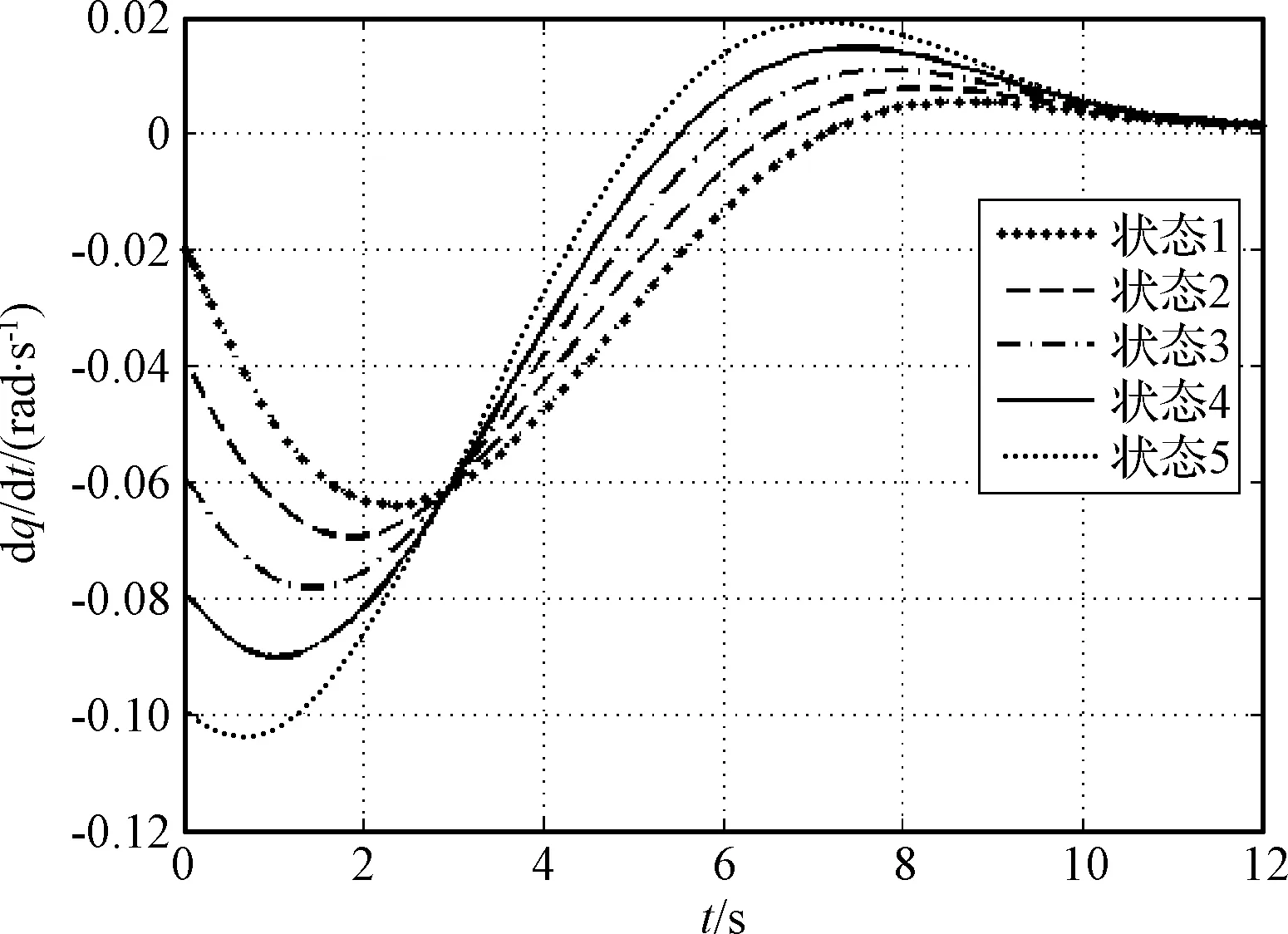
图12　防御器视线角速率变化曲线Fig.12　LOS angle rotation ratecurves of defender

初始状态终端拦截角脱靶量/m1-15．06°0．332-15．09°0．413-15．11°0．664-15．07°0．655-15．13°0．71

由图11～12和表4的仿真结果可知，防御器在不同的初始发射条件下，拦截角在有限时间内均能够收敛到-15°，视线角速率均能收敛到0附近，且防御器具有较小的脱靶量。表明基于有限时间理论的协同制导律对不同的初始发射条件有较强的适应性和鲁棒性。

4　结　论

本文针对高价值飞行器有效突防问题，采用一种三体协同突防方案，并基于有限时间理论给出了协同制导律设计方法。在假设三个飞行器具有一阶动力学特性的情况下，根据不同情况建立了两种反拦截数学模型，并根据控制器设计方法，解算了协同制导律。仿真结果表明：基于有限时间的协同制导方法能够保证拦截角和视线角速率在有限时间内收敛到预定值，防御器能够成功拦截拦截器；相比于突防器不配合引诱机动的情况，协同突防具有更大的优势；所提协同制导方法对不同的拦截角和初始发射条件均有较强的鲁棒性。

对于飞行器协同突防问题，本文在理论上给出了一种三体协同制导方法，但是在工程应用中还有许多实际困难需要解决，比如如何克服携带防御器对突防器自身状态造成的影响、如何有效协同估计和探测对方拦截器飞行状态等问题，这些都需要在后续研究中进一步考虑。

[1]姚郁, 郑天宇, 贺风华, 等. 飞行器末制导中的几个热点问题与挑战[J]. 航空学报，2015, 36(8): 2696-2716. [Yao Yu, Zheng Tian-yu, He Feng-hua, et al. Several hot issues and challenges in terminal guidance of flight vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2696-2716.]

[2]李庆春, 张文生, 韩刚. 终端约束条件下末端制导律研究综述[J]. 控制理论与应用，2016, 33(1): 1-12. [Li Qing-chun, Zhang Wen-sheng, Han Gang. Review of terminal guidance law with terminal constraints[J]. Control Theory and Applications, 2016, 33(1): 1-12.]

[3]Boyell R L. Defending a moving target against missile or torpedo attack[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, 12(4): 522-526.

[4]Boyell R L. Counterweapon aiming for defense of a moving target[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980, 16(3): 402- 408.

[5]Yamasaki T, Balakrishnan S N. Triangle intercept guidance for aerial defense[C]. The AIAA Guidance,Navigation, and Control Conference, Toronto, Canada, August 2-5, 2010.

[6]Ratnoo A,Shima T. Line-of-sight interceptor guidance for defending an aircraft[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 522-532.

[7]Shima T. Optimal cooperative pursuit and evasion strategies against a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2011,34(2): 414- 425.

[8]Prokopov O,Shima T.Linear quadratic optimal cooperative strategies for active aircraft protection[J].Journal of Guidance, Control, and Dynamics, 2013, 36(3): 753-764.

[9]Weiss M, Shima T,Castaneda D, et al. Combined and cooperative minimum-effort guidance algorithms in an active aircraft defense scenario[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(5): 1241-1254.

[10]Kumar S R,Shima T. Cooperative nonlinear guidance strategies for aircraft defense[J]. Journal of Guidance, Control, and Dynamics, 2017,40(1): 124-137.

[11]郭杨, 姚郁, 王仕成, 等. 一种基于有限时间理论的抗饱和制导律设计方法[J]. 宇航学报, 2012, 33(2): 175-182. [Guo Yang, Yao Yu, Wang Shi-cheng, et al. An anti-saturation guidance law designed by finite-time theory[J]. Journal of Astronautics, 2012, 33(2): 175-182.]

[12]郭杨, 姚郁, 王仕成, 等. 基于有限时间H2性能指标的导弹机动突防策略设计[J]. 宇航学报, 2010, 31(10): 2289-2294. [Guo Yang, Yao Yu, Wang Shi-cheng, et al. Finite-timeH2performance measure-based strategy design[J]. Journal of Astronautics, 2010, 31(10): 2289-2294.]

[13]Guo Y, Yao Y, Wang S C, et al.Maneuver control strategies to maximize prediction errors in ballistic middle phase[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(4): 1225-1234.

[14]刁兆师, 单家元. 带末端攻击角约束连续有限时间稳定制导律[J]. 宇航学报, 2014, 35(10): 1141-1149. [Diao Zhao-shi, Shan Jia-yuan. Continuous finite-time stabilization guidance law for terminal impact angle constrained flight trajectory[J]. Journal of Astronautics, 2014, 35(10): 1141-1149.]

[15]Golestani M, Mohammadzaman I. PID guidance law design using short time stability approach[J].Aerospace Science and Technology, 2015, 43(6): 71-76.

[16]张鹏. 基于有限时间系统理论的多飞行器协同拦截问题研究[D]. 哈尔滨：哈尔滨工业大学, 2013. [Zhang Peng. Research on cooperative interception using multiple flight vehicles based on finite-time system theory[D]. Harbin: Harbin Institute of Technology, 2013.]

[17]Bhat S P, Bernstein D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766.

[18]Amato F, Ambrosino R, Cosentino C, et al. Input-output finite time stabilization of linear systems[J]. Automatica, 2010, 46(9): 1558-1562.

[19]孙雪娇, 周锐, 吴江, 等. 多导弹分布式协同制导与控制方法[J]. 北京航空航天大学学报, 2014, 40(1):120-124. [Sun Xue-jiao, Zhou Rui, Wu Jiang, et al. Distributed cooperative guidance and control for multiple missiles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(1): 120- 124.]

[20]马国欣, 张友安. 多导弹时间协同分布式导引律设计[J]. 控制与决策, 2014, 29(5) : 843-847. [Ma Guo-xin, Zhang You-an. Time-cooperative distributed guidance law design for multi-missiles[J]. Control and Decision, 2014, 29(5): 843-847.]

[21]Zhang Y A, Wang X L, Wu H L. A distributed cooperative guidance law for salvoattack of multiple anti-ship missiles[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1438-1450.

[22]张春妍, 宋建梅, 侯博, 等. 带落角和时间约束的网络化导弹协同制导律[J].兵工学报, 2016,37(3):431-438. [Zhang Chun-yan, Song Jian-mei, Hou Bo, et al. Cooperative guidance law with impact angle and impact time constraints for networked missiles[J]. Acta Armamentarii, 2016, 37(3): 431-438.]

[23]丁世宏, 李世华, 罗生. 基于连续有限时间控制技术的导引律设计[J]. 宇航学报, 2011, 32(4): 727-733. [Ding Shi-hong, Li Shi-hua, Luo Sheng. Guidance law design based on continuous finite-time control technique [J]. Journal of Astronautics, 2011, 32(4): 727-733.]

[24]Amato F, Carannante G,Tommasi G D, et al. Input-output finite-time stability of linear systems: necessary and sufficient conditions[J]. IEEE Transactions on Automatic Control, 2012, 57(12): 3051-3063.

[25]Shaked U, Suplin V. A new bounded real lemma representation for the continuous-time case[J]. IEEE Transactions on Automatic Control, 2001, 46(9): 1420-1426.