考虑模态质量耦合的随机振动准静态载荷计算

杨新峰, 单悌磊, 扈勇强, 辛　强, 王海明

(航天东方红卫星有限公司, 北京 100094)

0　引　言

航天器及其组件在发射及地面运输中要经受包括随机振动在内的复杂力学环境[1]。因此，其结构设计要考虑随机振动相关的载荷。 当前，随机振动环境下的结构强度设计载荷依据主要是由随机振动等效而来的准静态加速度载荷。随机振动的等效准静态加速度载荷计算方法有多种[2-3]，大致可以分为两大类，一类是基于随机振动响应谱计算得到的准静态加速度载荷，一类是基于随机振动输入谱计算得到的准静态加速度载荷。

使用随机振动输入谱计算准静态载荷的方法则主要有试验规范法、Miles方法、模态质量参与法等。试验规范法是直接使用随机振动激励条件的总均方根加速度乘以3.0(即随机中3σ准则)作为准静态加速度，此方法理论上适用于刚体(即没有响应放大)，对于一般结构其计算结果十分保守。Miles方法[7]是基于均匀加速度输入谱下单自由度振动系统推导的，因此，Miles方法主要针对单一主模态结构，它根据随机振动加速度输入谱、结构的固有频率及阻尼三个参数计算出随机振动等效准静态加速度。Miles方法不能直接用于多模态结构，为了考虑一般结构的多模态特性，在Miles方法的基础上，产生了模态质量参与法，这种方法把每个模态的Miles算法的结果按模态质量参与的比例求和。可以看到,模态质量参与法是计算多模态结构随机振动准静态载荷的主要方法。然而，经过分析发现，目前的模态质量参与法并不是全面的方法，它忽略了模态质量耦合项的影响，这对于多模态结构中存在密集模态等情况时计算结果误差较大，无法适用。为此本文基于多自由度振动方程分析给出复杂模态结构的准静态加速度计算的完整形式，并针对密集模态状态给出计算准静态加速度的简便公式。

1　基于输入谱的随机振动准静态载荷基本理论

对于受随机振动激励的单自由度系统，准静态加速度载荷计算为如下Miles公式[7]：

(1)

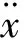
对于多自由度系统或多模态结构，各模态对准静态载荷都有贡献，但由于随机振动总能量在各个模态上分散了，往往最终随机振动的准静态载荷变小。Wijker[8]认为多自由度系统振动方程可以利用正交模态变换为模态坐标上的一组单自由度振动方程，每个单自由度的准静态加速度可由Miles方法得到，而总的准静态加速度由每个模态的准静态加速度乘模态质量比之后求和，这即是当前的模态质量参与法：

(2)

模态质量参与法把模态坐标上的各准静态加速度按模态质量比直接相加，实际上并没考虑全面的参与项，一些项被忽略了，最终计算结果的正确性或精度也取决于所忽略项的大小，下面推导随机振动准静态载荷基于模态质量参与法计算的完全形式，并针对密集模态情况进行分析，给出密集模态的简单计算公式。

2　随机振动准静态载荷计算的完全模态质量参与法

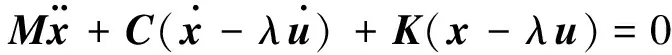
(3)

式中M,C,K分别为质量矩阵、阻尼矩阵和刚度矩阵，而λ=[1 2 …n]T,n为系统自由度。

设z=x-λu，那么式(3)可表示为：

(4)

式(4)的振动方程的正交模态矩阵记为Φ，根据模态理论，存在模态坐标变量q，有z=Φq。那么，式(4)可以经过模态变换解耦为多个单自由度振动方程：

(5)

(6)

对上式两边进行傅里叶变换得到：

那么有：

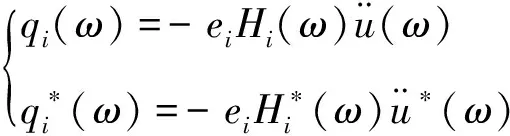
(7)

系统中与基础相连的单元刚度记为kn，相对于基础的位移记为zn，那么knzn为系统作用于基础的力，即基础传递给系统的力。可以验证knzn为矩阵Kz的各行相加之结果，因此作用于基础的力为：

(8)

用模态坐标表示则有：

f=λTKΦq

(9)

根据模态理论[10]，ΦTKΦ=Ω,ΦTMΦ=I，其中I为单位矩阵，

那么，

KΦ=(ΦT)-1Ω=MΦΩ

(10)

把式(10)代入式(9)中得到：

f=λTMΦΩq

(11)

由于eT=λTMΦ，则式(11)变为

根据随机谱理论[8,11]，f的功率谱为

(12)

把式(7)代入式(12)，得到：

(i≠j)

(13)

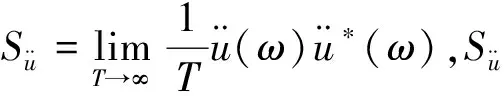
(14)

力f的总均方和为：

(15)

Gf除以系统总质量Mg的平方即为准静态加速度均方和：

(i≠j)

(16)

上式中第一项即为式(2)所示的模态质量参与法的结果，因为根据Miles公式有

式(16)其它项为模态耦合项，是目前模态质量参与法没有的。可见式(16)包含各阶模态质量的贡献以及耦合模态质量的贡献，是完全的模态质量参与形式。

式(16)中耦合项积分有定值[12]，可以写成下列形式

其中

那么，基于完全模态质量参与的准静态加速度均方和可以进一步写成

(17)

式(17)是另一种形式的完全模态质量参与法。第一项为单独模态质量参与项，第二项为不同模态质量耦合参与项。

3　模态质量耦合对随机振动准静态加速度的影响

在完全模态质量参与法中，模态耦合项表现为模态质量比的耦合以及频率响应函数的耦合。根据文献[12]，当系统固有频率隔离比较大或比较稀疏时，不同频率响应函数耦合的积分结果很小可以忽略，当系统固有频率比较接近或比较密集时，不同频率响应函数耦合的积分结果将具有较大的值，不可忽略。因此，模态质量参与法式(2)只是适用于稀疏模态的结构。

令α为两个模态的耦合项与非耦合项之比，λ为两个模态的模态质量比之比，则

(18)

式中，r为两模态频率之比，用以表示两模态密集程度 ，r=1表示两模态完全接近。λ表示两阶模态的模态质量之比，对于式(18)来说，λ大于1和λ小于1所表述的特性相同。对于一般结构低阶模态质量大于高阶模态质量，即λ≥1，因此这里以λ≥1来分析特性。对于不同λ值，α随r的变化曲线见图1。α值表示模态质量耦合影响大小，α越大表示模态质量耦合项占比越大。 计算中阻尼ξ取0.05。

图1　模态质量耦合项影响随频率比和模态质量比改变的变化曲线Fig.1　Variationof effects of modal mass coupling by changing frequency ratio and modal mass ratio

从图1可以看到λ=1时，当r≤0.75,α则小于0.1，即当固有频率之比小于0.75，模态耦质量合项的值会较小，小于非耦合项的10%，但当两个频率接近时(即r=1)，模态质量耦合项的值与非耦合项相当(α=1)，如果忽略模态质量耦合项，准静态加速度均方和的误差将达到约100%，准静态加速度均方根的误差约41.4%。λ变大后，耦合项的作用减小，但在当两个频率接近处，仍占相当的比例，如λ为3及r接近于1时，模态质量耦合项的值与非耦合项值之比约0.6。因此，固有频率接近时，即密集模态存在时，耦合项的模态质量对准静态加速度载荷的贡献不可忽略。

图2　忽略模态质量耦合导致5%准静态载荷误差的分界曲线Fig.2　Demarcation curve of 5% quasi-static load computation error due to omitting modal mass coupling

准静态加速度均方和的误差10%将产生约5%的准静态加速度均方根的误差，即5%的力均方根的误差，以此误差为控制条件(即α=0.1)，得到5%误差条件曲线如图2所示。根据图2，当r和λ取值在曲线的左边区域，那么忽略模态质量耦合项所产生的准静态加速度误差低于5%，因此对最终随机振动准静态加速度结果影响不大，而当r和λ的值落在图2曲线的右侧区域，忽略模态质量耦合项所产生的准静态加速度误差大于5%，则模态质量耦合项不可忽略。可以看到，当r<0.743，不论两阶模态质量之比如何，忽略模态质量耦合项的所产生的误差都较小，即准静态加速度计算结果误差小于5%，这也就是说，只要两模态频率之比小于0.743，则可以不考虑模态质量耦合项，使用公式(2)计算准静态加速度载荷也有足够的精度。同时也看到，两阶模态质量之比λ≥20时，不论两阶频率之比如何，模态质量耦合项的贡献也不大，可以忽略。需要说明的是这里参与计算的模态是指结构的主要模态，如一般结构的一、二阶主模态。图2展示的是两阶模态的情况。因为一般结构也是前两阶模态为主要模态，其他模态所占比重较小而在准静态载荷计算中一般可以忽略，以两阶模态进行分析模态质量耦合影响具有代表性。对于一般结构，越高阶的模态质量，一般其值越小，高阶模态质量耦合影响更小，因此，多阶模态按两阶模态分析得到的耦合项影响一般也是最大情况，可以覆盖多阶模态的误差。

4　密集模态的随机振动准静态载荷简便计算方法

式(16)中频率响应函数的耦合项可展开写为

(19)

两个模态密集或接近时，ωi=ωj，上式可以简化为

2|Hi(ω)||Hj(ω)|

(20)

那么，根据式(16),两个接近模态(第i阶模态和第j阶模态)的随机振动准静态加速度为

|Hj(ω)|]dω

(21)

由于两个频率接近，频率响应函数在全频段积分值比较接近，可以两个频率的平均值ωm来表示。式(21)可以表示为

(22)

ωm=(ωi+ωj)/2,上式积分进而可以用Miles 公式的形式表示为

(23)

为了比较式(23)和精确计算式(17)的计算误差，把式(23)和式(17)右侧相减并除以式(17)右侧得到准静态加速度均方和误差ε。简化后即为

(24)

式(24)表示两个模态情况下用精确式和简便式计算的相对误差。

两个模态情况下，对于不同模态质量比λ，ε随模态频率比r的变化曲线见图3。

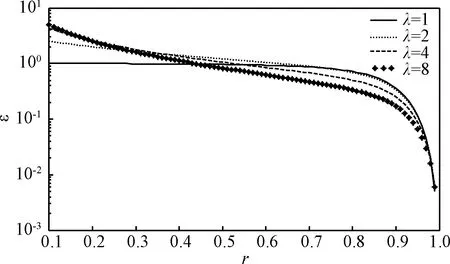
图3　密集模态的简便计算公式的误差Fig.3　The computation error of the simplified method for dense modes

可以看到随着模态频率比r增大，式(23)计算误差减小。对于λ=1，当r≥0.95，准静态加速度均方和误差将小于10%，也即准静态加速度均方根误差小于5%。模态质量比λ增大后，相同的模态频率比r所对应的计算误差进一步减小，但差别不显著。因此，可以r≥0.95作为式(23)的计算条件，即式(23)适用于r≥0.95的密集模态的准静态加速度计算。r<0.95时，随机振动的准静态加速度计算则需要利用式(16)或式(17)。

一般情况下，稀疏模态和密集模态可能会同时存在，则需要把稀疏模态的加速度平方与密集模态的加速度平方相加。因此，包含稀疏模态和密集模态的准静态加速度均方根为

aquasi=

(25)

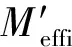
考虑3σ准则的最大准静态加速度载荷则为

aquasi-max=

(26)

5　密集模态的随机振动准静态载荷算例

两个矩形薄板的四角由四根梁连接而形成的结构在四根梁的根部受S=0.01g2/Hz的随机振动加速度谱激励(激励方向为垂直板面，即Z向)，激励频段范围为1～2000 Hz。板的尺寸为1×1 m2，板间距0.01 m，两板的厚度分别为3 mm和3.1 mm，梁的截面尺寸为0.01×0.01 m2。板与梁的材料为铝合金，总质量约16.5 kg。结构的有限元模型见图4所示。

图4　结构的有限元模型Fig.4　Finite element model of the structure

通过有限元模态分析得到结构的Z向前6阶固有频率和模态质量比，如表1所示。表中数据显示上述结构具有密集模态。

表1　结构的模态特性Table 1　Modal results for the structure

从表1看到1阶、2阶模态是比较接近的模态(频率比f1/f2=0.971)，3阶、4阶以及5阶、6阶也是接近的模态(f3/f4=0.969，f5/f6=0.970)，也即有3个密集模态对，但3个密集模态对之间频率间隔较远，因此，依据式(25)，3个密集模态对可分别按密集模态计算准静态加速度均方和，然后相加得到总准静态加速度均方和，最后开根号得到准静态加速度均方根。由式(25)计算得到准静态加速度均方根(取Q=10)为9.87g，乘以总质量换算为准静态力均方根为162.8N。由于本例前两阶模态质量比占结构的主要部分，其它模态占比较小以致可以忽略，因此，只用前两阶模态计算也可到达较精确结果。为验证方法，这里仍使用6阶模态进行计算。

由于结构简单，基于有限元的随机振动分析也可得到比较精确的四个角支反力功率谱曲线如图5。分析中，在四根梁的根部输入S=0.01g2/Hz的随机振动加速度谱，阻尼取为0.05。由图5可知一个角的支反力均方根为40.35 N，总的支反力均方根为161.4 N。与式(25)计算结果一致。

图5　随机振动激励下结构一个支撑点的支反力功率谱Fig.5　Reaction force power spectrum at one corner of the structure under random vibration excitation

式(25)计算结果、有限元计算结果以及模态质量参与法计算结果的比较见表2所示。可以看到计算密集模态的计算结果与仿真分析结果接近。而模态质量参与法计算结果较小，原因主要是没有考虑密集模态的模态质量耦合影响。对主要模态比较密集的结构，使用模态质量参与法计算随机振动准静态加速度或准静态力会导致较大的误差。

表2　不同计算方法的随机振动准静态力比较Table 2　Comparisons of quasi-static loading under random vibration using different calculation methods

6　结　论

本文利用模态理论和随机谱理论推导得到了改进的模态质量参与法，是同时可以考虑模态质量耦合影响的完全模态质量参与法，解决了原模态质量参与法计算密集模态时准静态载荷结果误差较大问题。

以两阶主要模态为代表进行分析，得到模态质量耦合影响与模态频率比和模态质量比的关系，模态越接近:模态质量耦合对随机振动准静态载荷贡献越大，同时模态质量比越接近也会增加模态质量耦合的影响作用。一般情况下，模态频率比小于0.743时或者模态质量比大于20时，模态质量耦合的影响可以忽略，可以看做模态稀疏情况而使用原模态质量参与法，反之,一般需要考虑模态质量耦合影响，需要使用本文改进的模态质量参与法。

针对模态频率比大于0.95的密集模态结构，本文还给出随机振动准静态加速度计算的简便计算公式。文中算例验证了所给方法的正确性。

[1]马兴瑞，韩增尧，邹元杰，等. 航天器力学环境分析与条件设计研究进展[J].宇航学报, 2012, 33(1):1-12. [Ma Xing-rui, Han Zeng-yao, Zou Yuan-jie, et al. Review and assessment of spacecraft mechanical environment analysis and specification determination[J]. Journal of Astronautics, 2012, 33(1):1-12.]

[2]杨宝宁.随机振动条件下设计载荷的确定方法[J].航天器工程，2006, 16(3):33-37.[Yang Bao-ning. Engineering methods for determining quasi-static limit load for structures under random vibration [J]. Spacecraft Engineering, 2006, 16(3):33-37.]

[3]Chung Y T, Krebs D J, Peebles J H.Estimation of payload random vibration loads for proper structure design[C].The 42th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference and Exhibit. Seattle, USA, April 16-19, 2001.

[4]张玉梅,韩增尧,刘绍奎. 航天器随机振动设计载荷比较[J]. 中国空间科学技术, 2013, 33(2):7-12.[Zhang Yu-mei, Han Zeng-yao, Liu Shao-kui. Comparisons of design loads under random vibration for spacecraft[J]. Chinese Space Science and Technology, 2013, 33(2):7-12.]

[5]邹元杰. 基础激励和声激励下的设计载荷估算方法[C],结构动力学会议论文集. 北京: 中国振动工程学会, 2009: 93-101. [Zou Yuan-jie. Estimation of design loads under random and acoustic vibration[C].The Proceedings of Structural Dynamics Conference，Beijing：China Vibration Engineering Academy，2009：93一101.]

[6]杨新峰，辛强，单悌磊，等.激励频段对航天器随机振动载荷的影响[J].航天器环境工程, 2016,33(6):581-588.[Yang Xin-feng, Xin Qiang, Shan Ti-lei, et al. The influence of frequency on the random vibration load of spacecraft[J]. Spacecraft Environment Engineering, 2016,33(6):581-588.]

[7]Miles J W. On structural fatigue under random loading[J]. Journal of Aerospace Science, 1954, 21(11):753-762.

[8]Wijker J. Random vibrations in spacecraft structures design[M]. New York: Springer, 2009.

[9]Majed A, Henkel E E, Component effective modal mass [C], The 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, Rhode Island, USA, May 1-4, 2006.

[10]Dimarogonas A. Vibration for engineers (second edition) [M]. New Jersey: Prentice-Hall, 1996.

[11]周荫清.随机过程理论[M].北京:电子工业出版社,2006.

[12]Clough R, Penzien J. 结构动力学[M]. 王光远 等译. 北京:高等教育出版社, 2006.