基于ZGS的大规模多智能体系统的分布式优化算法

夏海琪

（1.中科院上海微系统与信息技术研究所上海200050；2.上海科技大学上海201210）

网络技术的蓬勃发展，智能电网[1]、通信网络、神经网络、无线传感网络[2]等等各类大规模的不同形态的网络系统无不在人类的生活生产和发展中起着至关重要的用。而利用分布式优化技术解决这一类大规模多智能体系统网络[3-4]的优化问题便是近年来在这个研究方向最热门的主题之一。通过图论的知识根据多智能体系统的实际情况确定网络的拓扑结构，然后利用分布式优化算法将优化问题的数据或决策变量分布至网络中，使单个节点根据自身掌握的信息对最优决策进行估计，并通过与相邻节点间协作性的信息交互，不断修正自身的决策变量，最终实现全网络的优化问题。前几年提出的当前热门的分布式优化算法之一zero-gradient-sum（ZGS）算法[5-6]相比于传统的基于梯度的坐标下降优化算法[7]、分布式对偶算法[8-10]、ADMM[11-13]等算法计算量更小，信息交互少，收敛效果好，使得它在大规模无线通信传感器等类似多智能体网络上有极大的应用前景。然而更快，更高效，通信量更少的分布式优化算法才更能适应当前大数据背景下的大规模多智能体网络系统的发展。本文以此为出发现，结合ZGS算法思路设计了一个新的算法Accelerated-Zero-Gradient-Sum（AZGS）。相比于原有算法收敛效果更快，通信量更少，更加高效。以下正文利用非线性优化理论、图论、分布式计算模型等理论对新算法更高效得解决多智能体系统的一致性[12-13]进行分析。

1 模型阐述

考虑由n个多智能体组成的网络，通过特定拓扑中的无向连接，其网络拓扑图为G=(V，E(k))。其中：k∈N*={1，2，3，...}，代表不同的时刻；V={1，2，3，...，n}，表示网络拓扑图的节点集；E(k)={(i，j):i，j∈V，i≠j}，表示网络拓扑图的边集，代表在k时刻节点i和节点j之间可以相互通信。因为是无向图，所以(i，j)=(j，i)。而对于一个多智能体网络系统，通常我们优化的目标可以表示为如下的优化问题：

F(x)=∑i∈Vfi(x)其中fi(x)表示拓扑网络中各个节点的损失函数且都是强凸函数：∇f(y)-∇f(x)T(y-x)≥λ‖y-x‖2，∀x，y∈RmX=[x1，x2，...，xn]，xi∈Rm为i节点的值，若对于 ∀i，j∈{1，2，...，n}，i≠j有xi=xj，表示拓扑网络中所有的节点i∈{1，2，...，n}信息达到一致，X*便是满足全局一致，同时达到整个网络损失和最小的最优解。我们的目标就是设计一种分布式的优化算法去求得这个值。

2 算法设计

在文献[5]中提出的Gossip算法便是基于以ZGS算法为基础提出的，它是一种解决分布式优化问题的新颖思路。它提出在网络迭代更新的过程中始终满足两个条件：

算法一：

Step2：随机唤醒一个节点i∈V，令其所其一邻节点（可通信节点）为j；

Step3：把节点j的损失函数fj和当前节点值xj传递给节点i；

Step5：节点i把更新后的xi(k)传递给所有相邻节点j；

Step6：对于j更新节点值xj←xi(k)；

Step7：重复Step2，直至收敛；

此算法是一种将一些经典的一致平均算法推广到分布式凸优化问题的算法。在迭代过程中，各节点的Lagrangian函数梯度之和始终为零。通过使节点变量之间的差距逐渐缩小至零，各节点变量将收敛至问题的最优解。这类算法的收敛性分析主要利用函数的凸性派生出的Lyapunov函数。各节点还可以利用该函数来独立决定执行更新和通信的时间点。它的优点是规避了常规优化算法迭代过程中的步长问题，而且能保证在具有时变拓扑结构的网络中实现渐进收敛，甚至获得收敛速度的保证。为了使得算法更加通用，如[14-16]是在此基础上在节点唤醒过程中采用非均匀分布的形式，考虑到各个节点在整个网络中所起到的作用不同赋予不同大小的权重。而本文则选择从另外两个不同方向在原有算法的基础上进行革新。

现实网络中，多智能体单次通信往往会传递许多数据，因此新算法把单个智能体的变量扩展到xi∈Rm，那么新算法的迭代条件变为：

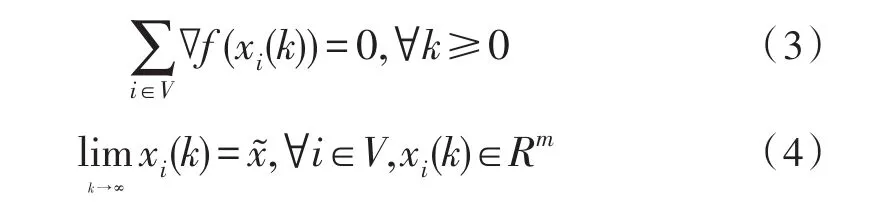
也因为网络的复杂性和数据维度的扩展，那么从更加节能和加快收敛的角度考虑对[6]中算法进行新的改进是必不可少的。首先是网络在唤醒某个节点的后，同时与其相邻的所有节点进行信息交互。主要在算法是在原有算法的基础上把每次迭代的邻节点j改为所有与节点i相邻的节点集Ni；另外考虑信息交互重复的问题，引入状态矩阵Zij，矩阵所有 元 素 初 始 值 为 1，同 时 ∀i，j∈{1，2，...，n}，∀k∈N*，Z(k)ij=Z(k)ji，当节点i被唤醒时，同时更新 ∀j∈Ni，若Zij为1，则损失函数fj（仅初次传递需要）和当前节点值xj传递给节点i，同时更新Zij为0，否则不传递。另外，因为所有节点j∈Ni更新之后，对于每个节点j对应的节点w∈Nj，w≠i，w∉Ni，更新Zjw为1；综合上述，设计出新的优化算法流程如下：

算法二：

Step1：初始化各个节点：xi←x*i；

Step2：随机唤醒一个节点i∈V，令其所其邻节点（可通信节点）的集合为Ni；

Step3：每个节点j∈Ni，若Zij=1把损失函数fj和（仅初次传递需要）当前节点值xj传递给节点i，若Zij=0，则不传递，并更新状态矩阵Z；

Step5：节点i把更新后的xi(k)传递给所有相邻节点j∈Ni；

Step6：对于 ∀j∈Ni更新节点值xj←xi(k)；

Step7：重复Step2，直至收敛；

3 算法收敛性分析

关于新算法的收敛性分析主要利用经典的李雅普诺夫稳定性方法[15]，定义李雅普诺夫候选函数为：

由于问题模型描述中已经定义fi(x):Rm→R的强凸性和连续可导性，我们有：

由式（5）和式（6）可以知道V(x(k))≥0，∀k≥0；所以要证明新算法收敛，只需要证明：

利用算法最初的限定条件（3）以及李雅普诺夫候选函数的定义我们可以得出：

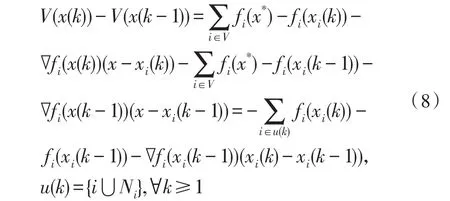
根据式（8）可知V(x(k))是非增函数。由此可知：

由原函数的强突性可得：

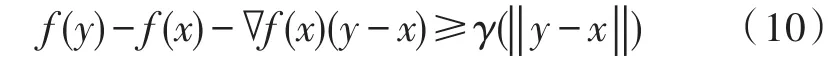
其中γ:[0，∞)m→[0，∞)，γ(0)=0 是连续严格递增函数。其证明可参照[5]定理4。然后根据式（9），式（10）可得：

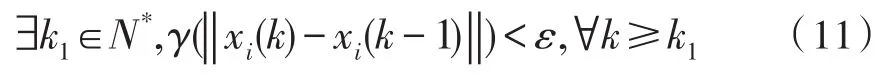
结合式（11）以及新算法step6得：

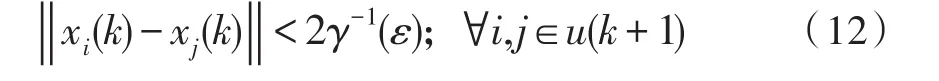
B={i∈V:‖xi(k1)‖≥‖xp(k1)‖}，那么当k>k1时，对于任意节点i∈A和任意节点j∈B，{i，j}≠u(k)这与网络的连通性，不存在独立节点相矛盾。故

从而当ε取很小的我时候，根据γ函数的定义可以得出式（7）成立，即：

实现全局最优以及整个多智能体网络的一致性任务。

4 算法仿真实验验证

对于上述算法的仿真，实验环境为matlab，网络规模为20个节点，首先根据算法模型的通过程序随机生成连通性网络拓扑结构如图1所示。

从图1中可以看到所模拟的拓扑图是根据定义的连通网络，既没有独立节点。其中的线段表示智能体之间能否进行信息交互。线段的长短模拟智能体之间的距离，与实际环境多智能体通过局部无线通信进行信息交互的可行性受距离因素所影响相一致。

图1 模拟多智能体网络拓扑图

然后通过文献[5]中的算法的对图1的多智能体网络进行仿真，结果如图2所示。

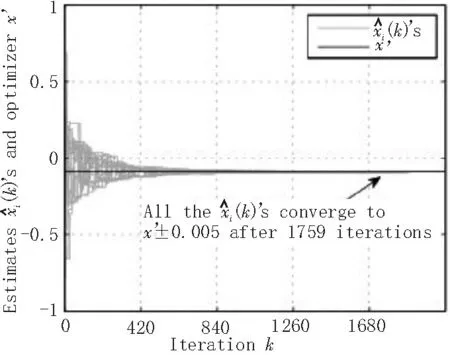
图2 原算法仿真结果

可以看出在大约1 750次迭代之后，网络一致性基本实现。新设计的算法的同样在图1的网络中进行仿真，结果如图3所示。

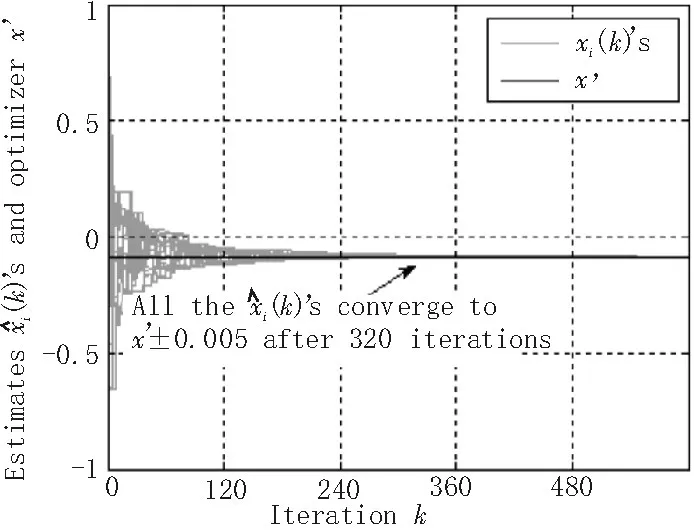
图3 新算法仿真结果

通过图2与图3的对比可以清晰看到原算法在迭代1750次以上能让网络图中的节点实现整体的一致性问题，而新算法在迭代320次以上就能实现很好的优化结果。另外，在仿真过程中引入Zij，看似并没有减少多智能体之间的通信过程次数，甚至有所增加。然而不难发现及时增加的通信次数，所传递的仅仅是Zij的值（0或1），而相当一部分这样的通信代替了原来需要传递的值xi∈Rm，在实际环境中m的值也往往比较大，那么进过新的信号传递方式在一定程度上增加了网络的通信次数，从单次信号传递的能量上就节约了将近m倍，同时提升信息传递速度。以传递一个数值为一次消耗计算，那么改进后的算法在图1这个模拟的多智能体网络为例，随着变量维度的增大于，其节省的计算消耗如图4所示。

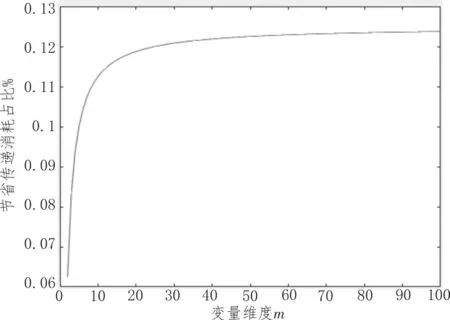
图4 变量维度与耗能节约关系

从图4中不难看出，变量维度m的增伴随着更大比例的能耗节约。即实际的m值比较大的情况下，改进的信息交互方式能进一步实现更快更节能的目的。这也契合大数据爆发时代高效，节能绿色通信的发展趋势。

5 结论

本次研究了基于ZGS算法方向的分布式优化算法。新提出的AZGS，改进节点信息的交互模式，结合李雅普诺夫方程，论证了新算法在通过分布式的方法解决了多智能体网络的一致性问题的前提下。实现了速度更快更快，信息交互更加节能。并在matlab环境下实现仿真验证。该结果有利于在实际多智能体通信网络中通过更加高效节能的交互方式解决问题。另外之后的研究工作会在多智能体信息交互的安全性考虑进一步研究，以实现多智能体网络更安全，更节能，更高效的绿色通信。

参考文献：

[1]李俊雄，黎灿兵，曹一家，等.面向智能电网的互动式节能调度初探[J].电力系统自动化，2013，37（8）:20-25.

[2]崔莉，鞠海玲，苗勇，等.无线传感器网络研究进展[J].计算机研究与发展，2015，42（1）:163-174.

[3]Barrat M Barthelemy，Vespignani A.Dynamical processes on complex networks[M].Cambridge University Press，2010.

[4]Ren W，Beard R W.Consensus seeking in multiagent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control，2005，50（5）：655-661.

[5]Lu J，Tang C Y，Regier P R，et al.Gossip algorithms for convex consensus optimization over networks[J].IEEE Transactions on Automatic Control，2011，56（12）：2917-2923.

[6]Lu J，Tang C Y.Zero-gradient-sum algorithms for distributed convex optimization:The continuoustime case[J].IEEE Transactions on Automatic Control，2012，57（9）：2348-2354.

[7]Bezdek J C，Hathaway R J，Howard R E.Local convergence analysis of a grouped variable version of coordinate descent[J].Journal of Optimization theory and applications，2013，54（3）：471-477.

[8]Johansson B，Soldati P，Johansso M.Mathematical decomposition techniques for distributed crosslayeroptimization ofdata networks[C].IEEE Journal on Selected Areas in Communications，2006，24（8）：1535-1547.

[9]Lu J，Johansson M.Convergence analysis of approximate primal solutions in dual first-order methods[J].SIAM Journal on Optimization，2016，26（4）:2430-2467.

[10]Larsson T，Patriksson M，Stromberg A-B.Ergodic，primal convergence in dual subgradient schemes for convex programming[J].Mathematical Programming，2009，86（2）：283-312.

[11]曹茂.无线传感器网络下基于分布式凸定位问题算法研究[D].重庆：重庆师范大学，2014.

[12]林静然，姜昌旭，利强，等.基于ADMM的分布式功率分配和接入控制联合优化算法[J].电子科技大学学报，2016，45（5）:726-731.

[13]Boyd S，Parikh N，Chu E，et al.Distributed optimization and statisticallearning via the alternating direction method ofmultipliers[J].Foundations and Trends in Machine Learning，2011，3（1）：1-122.

[14]杨洪勇，张嗣瀛.离散时间系统的多智能体的一致性[J].控制与决策，2009，24（3）:413-416.

[15]谢光强，章云.多智能体系统协调控制一致性问题研究综述倡[J].计算机应用研究，2011，28（6）:234-239.

[16]王长城，戚国庆，李银伢，等.量化状态信息下多智能体Gossip算法及分布式优化[J].电子与信息学报，2014（1）:128-134.

[17]俞辉，蹇继贵，王永骥.多智能体时滞网络的加权平均一致性[J].控制與決策，2007，22（5）:558-561.

[18]谭拂晓，关新平，刘德荣.非平衡拓扑结构的多智能体网络系统一致性协议[J].控制理论与应用，2009，26（10）:1087-1092.

[19]潘欢.二阶多智能体一致性算法研究[D].长沙:中南大学信息科学与工程学院，2012.