基于机器视觉的方块地毯边缘缺陷检测技术

方新茂，颜文旭，丁律

（江南大学物联网工程学院，江苏无锡214000）

在地毯的生产过程中，由于工艺水平的限制，工人的操作不当等因素经常造成地毯出现包括缺边、边缘切除不净等缺陷。带有缺陷的产品常常导致其价格大大降低。目前许多企业，尤其是中小企业对于地毯缺陷的检测仍然依靠人工目测的方法。这种方法在大批量的地毯生产检测中存在以下等几个问题：1）效率底下；2）标准不一，缺乏科学性，比较主观；3）工人易产生疲劳，影响工人身心健康，也将影响工人的检测准确率。因此，为了提升生产效率，提高判别科学性，解放劳动力，设计合理的地毯缺陷检测系统具有十分重要的意义。

1 系统设计

机器视觉是一门涉及人工智能、神经生物学、心理物理学、计算机科学、图像处理、模式识别等诸多领域的交叉学科[1]。机器视觉将视觉传感器采集到的待检测产品图像经计算机处理，特征提取，并对其进行理解、分析，将最终结果用于检测控制等。该方法可以提高检测效率和精度，同时大大提高生产效率和生产的自动化程度。基于机器视觉的方块地毯边缘缺陷检测系统，就是通过CCD相机采集到的图像经过工业计算机的处理，分析出地毯的缺陷状况。本文的地毯边缘缺陷检测系统简图如图1所示。

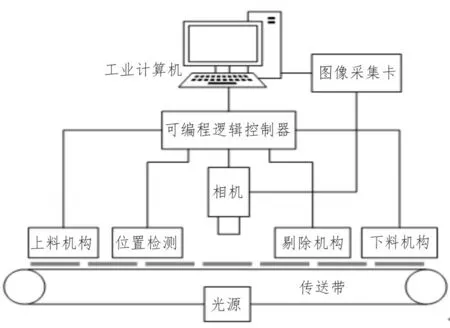
图1 系统总统框图

光源：照明系统对图像质量和图像软件处理的结果影响很大。由于地毯具有一定的厚度，一个光源可能会造成地毯的边缘产生阴影，影响地毯的边缘检测，采用多LED光源设计可以有效解决这样的问题。

视觉传感器：目前，在机器视觉的图像采集过程中，广泛使用CCD（Charge Coupled Device，电荷耦合器件）摄像机。CCD相机分为线阵CCD和面阵CCD。相比于线阵CCD只能获得一维图像，不能处理复杂的图像，面阵CCD可以获得二维图像，获得的信息量大，能处理复杂的图像，因此本文采用面阵CCD，型号是DH-SV401GC/GM，分辨率为780x582。

图2 CCD拍摄地毯实物图

2 边缘检测

CCD相机拍到的图像如图2所示，为了区分前景和背景，需要将地毯从背景中分割出来。常用的图像分割方法有基于阈值、基于边缘算子、基于区域、基于能量泛函等分割方法[3-7]。由于本文所检测的地毯式50 cm*50 cm的规则的正方形，所以只要检测出四条边缘所在直线就能分割出地毯的图像。

基于边缘算子进行检测的方法对于噪声过于敏感，而且对于本文的地毯，纹理部分的灰度值也会出现较大的梯度，图3是图2中接近中间某条横线所在位置的灰度值，容易发现，并不能保证其边缘都是陡峭的变化，再加上纹理部分也会出现梯度较大的部分，常常导致边缘检测错误。

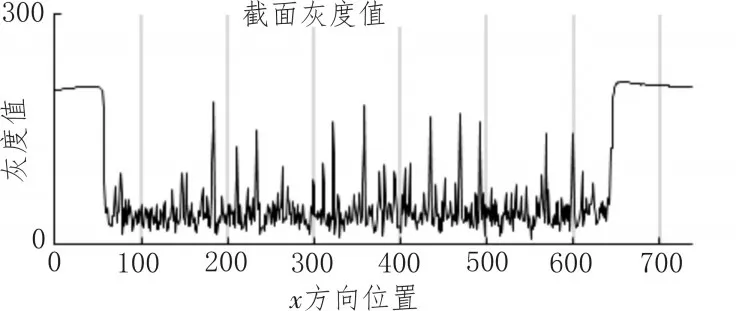
图3 截面灰度值曲线

目前应用范围较广泛且效果较好的边缘检测算法是基于Canny算子的边缘检测。这种方法具有良好的抗噪声能力，并且具有较高的检测精度[8-9]，但仍然无法处理本文中地毯的纹理和边缘，检测结果如图4所示，显然，纹理造成的孔洞并非我们想要的边缘。

图4 基于Canny算子的边缘检测

2.1 形态学运算

数学形态学是以形态结构元素为基础对图像进行分析的数学工具，被广泛应用于机器视觉处理领域[10]。形态学图像处理是将原图像与图像中一个移动的结构元素进行交、并等集合运算。基本的形态运算是腐蚀和膨胀。

在形态学运算中，结构元素是最重要的基本概念，它的作用相当于在信号处理中的“滤波窗口”的功能[11]。用B代表结构元素，图像A中的每一点x，腐蚀和膨胀的定义分别为：

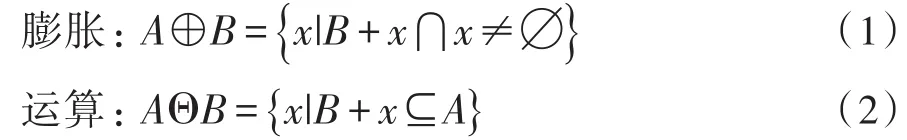
将结构元素B平移后使B包含于A的所有点构成的集合就是腐蚀后的结果。与之相反，将结构元素B平移后使A与B的交集非空的点构成的集合就是膨胀后的结果。形态学运算包含两个重要运算：开运算和闭运算[12]。先腐蚀后膨胀的过程称为开运算，用∘表示。它具有消除细小孤岛，分离细微连接以及对大物体边界滤波的作用。先膨胀后腐蚀的过程称为闭运算，用∙表示。它具有填充物体内细小孔洞，连接相近物体以及平滑边界的作用，从而达到滤波效果[13]。开运算和闭运算的表达式如下所示：

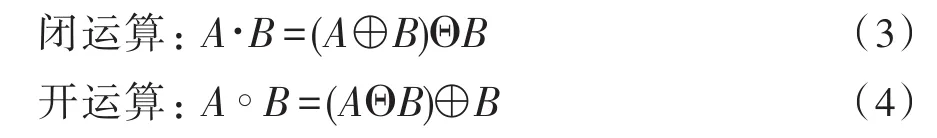
2.2 基于形态学运算的边缘提取

形态学边缘检测常用的有膨胀型、腐蚀型和形态学梯度边缘检测算子[14]。腐蚀型边缘检测过程是将原图像减去腐蚀后的图像而得到边缘，膨胀型边缘检测过程是将原图像膨胀后减去原图像得到图像边缘，形态学梯度边缘检测过程是原图像膨胀后减去原图像腐蚀后的图像得到图像边缘。形态学梯度运算使图像灰度级的跃变更为急剧。

2.3 基于双结构元素形态学边缘检测

本文利用地毯边缘形状的特殊性，将形态学滤波操作和边缘提取结合在一起，选取两个结构元素S1、S2，S1为5*5，原点为中心点的正方形结构元素，S2为3*3，原点为中心点的正方形结构元素。先对输入图像P以结构S1元素进行一次形态学膨胀运算得到图像A，对A以结构S2元素进行一次形态学腐蚀运算得到图像B，将A与B做差得到地毯的边缘。表示如下：

图像E即为图像的边缘。处理之后的结果经过了膨胀和腐蚀操作，相当于同时进行了闭运算滤波。

由于两个结构元素大小的差异，得到的边缘轮廓要比真实的边缘轮廓向外大一个像素。本文处理的地毯边缘是由四条直线构成的正方形，因此需将检测出来的这四条直线向内侧各平移一个像素才能得到反映真实图像边缘的直线。

2.4 直线拟合

最小二乘法是最简单的直线拟合方法，应用最为广泛，计算也比较简单[15]，但对于本文，边缘缺陷导致的边缘会将该方法下拟合的直线偏离真正的边缘。本文采用霍夫变换来检测边缘所在的直线，霍夫变换是图像变换中的经典变换之一，经典的霍夫变换可以从图像中检测出直线和圆，改进的霍夫变换可以检测出椭圆和其他的一些图形。霍夫变换实际是一种基于统计学的检测方法，最终检测出直线对应的一定是参数平面中直线相交最多的那个点，可以有效避免噪声的干扰[16-19]。

两种方法检测出来的效果如图5所示，上侧为霍夫变换检测结果，下侧为最小二乘法得到的结果，显然霍夫变换检测出来的直线更接近地毯真实的边缘。

图5 霍夫变换和最小二乘法直线拟合对比

3 缺陷检测

3.1 正方形程度

对于理想的无缺陷的地毯图案，地毯边缘所围成的四边形应近似于正方形，因此我们定义描述四边形的正方形程度如下：

式中a，b，c，d分别位四条边的长度，m=(a+b+c+d)/4，若该四边形是理想正方形，则S=0，反之，该四边形与正方形差异越大则S越大。

3.2 边缘缺陷

为了得到边缘缺陷状况，本文采用的方法是将地毯二值化图像和检测到的四边形做差，得到缺陷区域，再定义缺陷函数来判断是否是有缺陷。具体方法是在二值化的时候将背景部分灰度值设为0，地毯部分设为120，新建一副同样大小，灰度值均为120的图像，将检测到的四条边缘直线围成的四边形内部填充为0，最后两幅图像相加，得到缺陷结果图。图7是图6处理的结果，图中灰色（灰度值为120）表示正常的部分，白色（灰度值为240）表示缺边部分，黑色（灰度值为0）表示切除不净的部分，后两者均称为缺陷区域。

图6 带待检测图像

图7 缺陷处理结果图像

为定量描述边缘缺陷程度，本文将整幅图像分为如图8所示8个部分，1，2，3，4区域的缺陷取缺陷点到四边形在该区域边的距离，5，6，7，8区域缺陷取缺陷点到四边形在该区域的顶点的距离。

图8 缺陷区域划分

并定义缺陷特征函数为

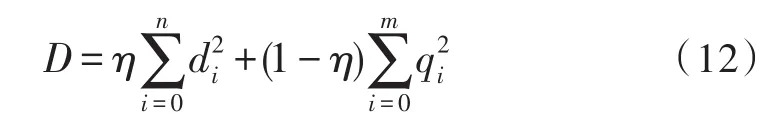
其中d表示地毯内部缺陷点到最近的边或点的距离，n表示地毯内部缺陷像素的个数，q表示地毯外部缺陷到最近的边或点的距离，m表示地毯外部缺陷像素的个数，η为内部缺陷所占比重，根据经验得出。

由于相机拍出来的图片发生了一些微小的畸变以及霍夫变换的精度影响，检测出来的直线不能完全反映地毯的边缘，如图中所示，即使没有缺陷的区域也会有细小而狭长的误检测区域，为了降低这部分区域的影响，在缺陷区域的遍历时，忽略一些较小的距离，这样做可以增大有无缺陷特征的差异。

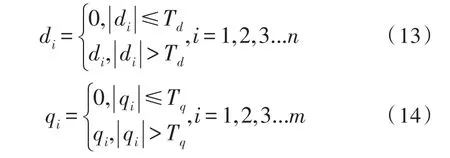
4 实验结果

在本文的方法中，只要对S和D分别进行简单的阈值比较就能对缺陷地毯进行较好的识别，对120张地毯图案进行检测实验，其中27张有缺陷，实验中，η=0.5，Td=Tq=0.5，S的判别阈值为0.02，D的判别阈值设为450。检测率为92.6%，误检测率为1.1%。结果表明，本文使用的方法能够较为准确的检测出缺陷，并且误检测率也较低。

5 结 论

对地毯常出现的缺边、边缘切除不净的缺陷，文中利用地毯边缘的特性，基于双结构元素的数学形态学运算，用两次形态学基本运算完成对原图像的滤波和边缘提取，相对传统的方法减少一次运算，提高了图像处理的速度。用霍夫变换检测出地毯边缘所在直线，并将四条边缘直线向内部移动一个像素以抵消两个结构元素差异带来的影响，能够真实的反映出地毯的边缘直线。最后将区域分块并定义缺陷特征函数，能够较准确、快速的检测出缺陷的地毯，同时具有较低的误检测率。

参考文献：

[1]朱铮涛，黎绍发.视觉测量技术及其在现代制造业中的应用[J].现代制造工程，2004（4）:59-61.

[2]刘斌，吴盛金，邹仕放.基于机器视觉的塑胶制品表面缺陷自动检测技术[J].塑料工业，2009（12）:5-9，15.

[3]刘松涛，殷福亮.基于图割的图像分割方法及其新进展[J].自动化学报，2012（6）:911-922.

[4]陈恺，陈芳，戴敏，等.基于萤火虫算法的二维熵多阈值快速图像分割[J].光学精密工程，2014（2）:517-523.

[5]郑毅，郑苹.基于模糊熵和模拟退火算法的双阈值图像分割[J].电子测量与仪器学报，2014（4）:360-367.

[6]赵泉华，高郡，李玉.基于区域划分的多特征纹理图像分割[J].仪器仪表学报，2015（11）:2519-2530.

[7]许新征，丁世飞，史忠植，等.图像分割的新理论和新方法[J].电子学报，2010（S1）:76-82.

[8]Canny J.A computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1986（86）:679-698.

[9]王小俊，刘旭敏，关永.基于改进Canny算子的图像边缘检测算法[J].计算机工程，2012（14）:196-198，202.

[10]肖大雪.浅析数学形态学在图像处理中的应用[J].科技广场，2013（5）:10-19.

[11]刁智华，赵春江，吴刚，等.数学形态学在作物病害图像处理中的应用研究[J].中国图象图形学报，2010（2）:194-199.

[12]王芳，钱炜，李文超.基于数学形态学的图像边缘提取方法[J].机械工程与自动化，2015（1）:46-48.

[13]李武周，余锋，王冰，等.基于形态学滤波的红外图像背景补偿[J].红外技术，2016（4）:333-336.

[14]冯永亮.基于数学形态学的图像边缘检测改进研究[J].河南科学，2016（6）:833-837.

[15]田垅，刘宗田.最小二乘法分段直线拟合[J].计算机科学，2012（S1）:482-484.

[16]X.N.Yu，Research and implementation of sub pixelpositioning technology based on hough transform[C]//2016 International Conference on Robots&Intelligent System（ICRIS），ZhangJiaJie，China，2016（62）:296-300.

[17]金守峰，陈蓉，范荻，等.面向机加工表面粗糙度的光切显微视觉测量系统[J].西安工程大学学报，2016（3）:347-353.

[18]李阳，彭博栋，盛亮，等.一种用于条纹相机图像的多尺度小波边缘检测算法[J].现代应用物理，2016（4）:54-60.

[19]李静，王新民.基于B样条小波的零件缺陷图像边缘检测[J].纺织高校基础科学学报，2011，24（2）:299-302.