液压支架顶梁的重量优化

2018-04-02杨彦华

机械管理开发 2018年3期

杨彦华

（山西焦煤集团有限责任公司东曲煤矿，山西　古交　030200）

引言

特厚煤层开采对液压支架的要求较高，工作面所选支架不仅要通过相关的强度试验和安全性试验，而且还需对关键构件进行重量优化[1-2]。在不影响支架工作性能的前提下减轻支架重量有利于支架在工作面的推移，同时还达到了节约成本和提高矿井效益的目的，大量现场实测结果表明，当支架顶梁中部受到集中载荷作用时，支架的受力情况最为糟糕。故本文再对特厚煤层采场液压支架的顶梁进行重量优化时设定顶梁边界约束条件为中部位置受集中应力作用，优化后的支架顶梁仍然会达到其他工况条件下的强度需求。

1　顶梁重量优化流程

顶梁重量的优化流程就是进行最优化设计，即基于最优化理论，综合考虑多种影响因子，依附于计算机语言求得最优方案。具体流程为：根据支架工作的实际环境建立等效模型，把影响因子视为边界约束条件，结合适合的优化方案以及计算机语言进行最优方案的求解[3-4]。本文通过Matlab进行液压支架顶梁的重量优化，具体优化流程如图1所示。

2　建立支架顶梁的等效模型

本文进行顶梁重量优化研究时，设定顶梁边界约束条件为中部位置受集中应力作用。该支架为4柱支架，各个支柱的支撑力均为5.6 kN，顶梁中部位置所受的集中应力为20 kN，在工作面液压支架受到多种载荷作用，图2为支架所受的剪力和弯矩特征。

在图2中，L1=0.63 m，L2=1.195 m，则根据静力平衡条件可求得：剪力Fs1=Fs6=5×103kN，Fs2=Fs3=Fs4=Fs5=10×103kN；弯矩 M1=M7=1.23×109N·mm，M2=M6=4.38×109N·mm，M3=M5=5.61×109N·mm，M4=17.56×109N·mm。顶梁是封闭且对称的箱体结构，如图3所示。

图1　液压支架顶梁的重量优化求解示意图

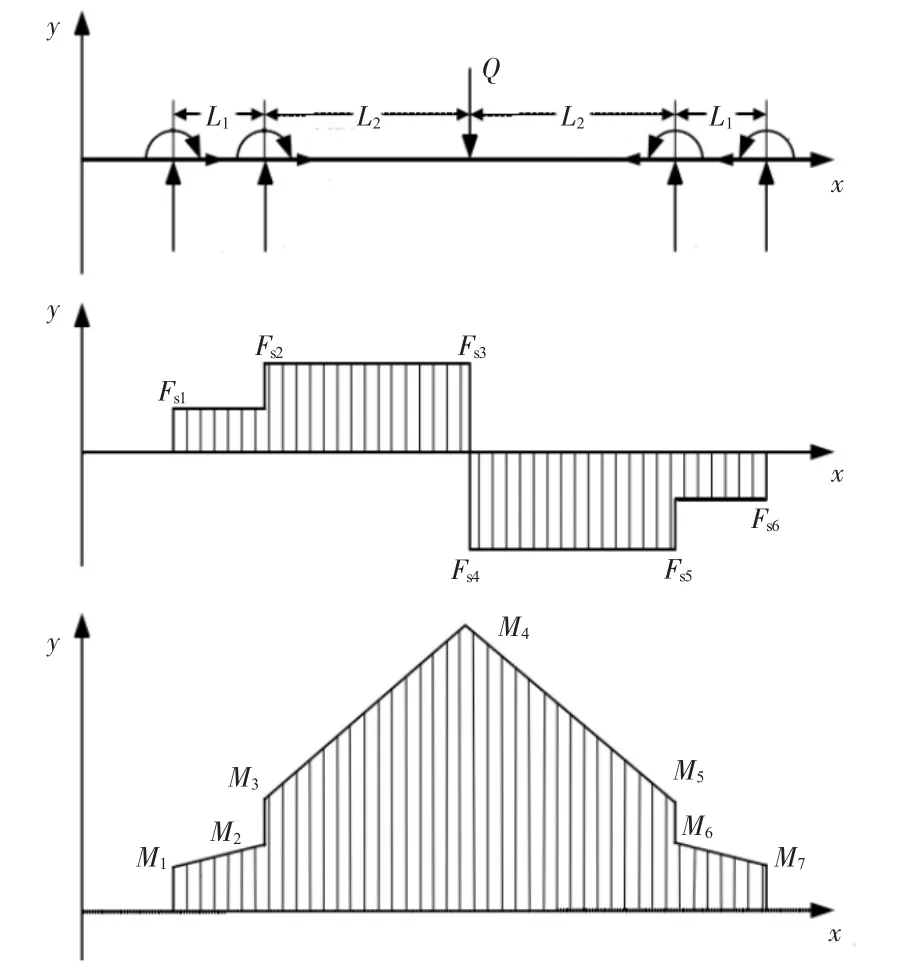
图2　液压支架顶梁所受的剪力和弯矩特征示意图

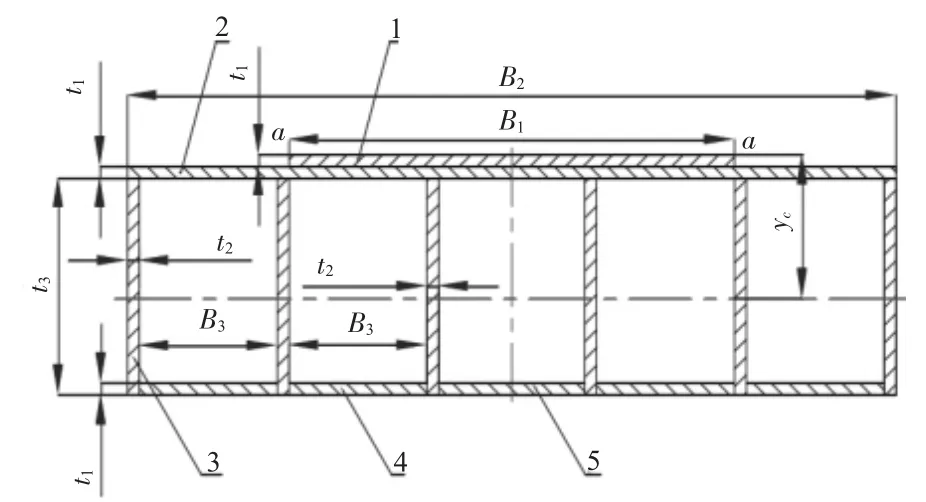
图3　液压支架顶梁结构示意图

根据图3计算顶梁的弯曲正应力，计算过程如下所示。

1）顶梁结构重心到图3的aa截面的距离yc如式（1）所示：

2）顶梁结构重心到各块板中心处的距离ai通过式（2）计算：

3）顶梁 1～5 号板中心的惯性距 J1—J5如式（3）所示：

4）顶梁各块板对形心的惯性距通过式（4）计算：

5）结合式（1）—（4）可求得顶梁的弯曲正应力，如式（5）所示：

顶梁的剪应力均值通过式（6）计算：

支架顶梁的边界受到剪应力和弯曲正应力的双重作用，则根据式（7）可计算得到等效应力σr：

3　支架顶梁优化结果分析

将支架顶梁的边界约束条件和目标函数转变为Matlab可识别的形式，顶梁中部位置受集中应力作用，该位置为容易发生塑性屈服，故对该位置的强度进行校核。为了使通过Matlab计算得到的最优解可以达到各种工况条件下的需求，应力集中位置的安全系数需要设置的更大一些。顶梁的板材厚为设计变量，如式（8）所示。

本次需要进行顶梁的重量优化，故最优重量可理解为最优体积，即要求顶梁的横截面积达到最小，故目标函数如式（9）所示。

支架顶梁等效应力的最大值应该低于极限强度，同时安全系数设置为1.8，由此得到式（10）。

顶梁的上边界条件和下边界条件如式（11）所示。

进行顶梁重量的最优化方案求解时需要注意：真实情况下支架顶梁的钢板设计尺寸是固定的，不是连续变量，而Matlab求解的是连续变量。但求解的目标函数在最优值附近的变化十分平缓，故对Matlab求解得到的最终结果取整便得到了顶梁重量的最优值。顶梁的初始参数如表1所示，求解得到的顶梁最优参数如表2所示。

表1　支架顶梁的初始参数统计表

表2　支架顶梁的最优参数统计表

对比表1和表2可以发现，计算得到额腹板高度和厚度均与开始设置的边界值基本相符，说明最优参数求解所得的结果受开始设置边界值的影响较大，故在最优值求解前需要设置合理的边界值。支架顶梁厚度由腹板的高度决定，一般情况下顶梁厚度是支架升柱高度最大值的10%，腹板高度为0.68 m，而其长度为6.8 m，腹板处于顶梁的纵向位置，为了保证腹板在受载作用下依然保持较高的刚度，故腹板厚度设计为15 mm，这就得到了表2中顶梁的最优参数。将表2中顶梁的最优参数进行标准化处理，由此得到的最优标准参数如下页表3所示。

表3　支架顶梁的最优标准参数统计表

对表3中的两个方案进行比较可以发现，方案一顶梁重量减轻了18%，要优于方案二，但方案一下顶梁的截面积要小于方案二；顶梁所用材料的极限强度为380 MPa，屈服强度为700 MPa，而方案一下等效应力为394 MPa，处于极限强度和屈服强度之间，方案二等效应力为375 MPa，处于极限强度以下，从矿井安全开采的角度分析，方案二要更优一些。

4　支架顶梁变量的敏感性分析

在支架顶梁的各项参数中，重量最优值受腹板的高度和厚度以及盖板厚度的影响，但各因素的影响程度不同，故需要对这三个影响因素的影响效果（敏感性）进行定量评价，顶梁等效应力最大值与这三个因素间的关系如图4所示。

图4　顶梁等效应力最大值与各个因素间的关系示意图

从图4中可以看出，顶梁等效应力最大值与各因素均呈现为负相关关系，但随着横坐标的增大，等效应力最大值的减小速率不同，按从高到低的顺序可排为：盖板厚度>腹板厚度>腹板高度，由此说明对顶梁等效应力的影响效果可排为：盖板厚度>腹板厚度>腹板高度。顶梁截面积与这三个因素间的关系如图5所示。

从图5中可以看出，顶梁截面积与各因素均呈现为正相关关系，但随着横坐标的增大，等截面积增大的速率不同，按从高到低的顺序可排为：盖板厚度>腹板厚度>腹板高度，由此说明对顶梁截面积的影响效果可排为：盖板厚度>腹板厚度>腹板高度。

综合而言，盖板厚度与初始值较为相符，究其原因，盖板厚度对顶梁截面积的影响效果最为显著，但当盖板厚度过小时，则顶梁的等效应力过大，很容易导致材料发生塑性屈服。腹板厚度对顶梁截面积和等效应力的影响效果也较为明显，故对支架顶梁进行重量优化时主要可以通过减小腹板厚度的手段来实现，通过对比表1—表3也发现腹板厚度减小的程度最大。腹板高度对顶梁截面积和等效应力的影响效果不是十分明显，故可以通过以减小腹板高度为辅的手段来进行顶梁重量优化。