一种解决组合公钥密钥碰撞的方案

2018-04-02陈亚茹

信息安全研究 2018年3期

陈庄陈亚茹

(重庆理工大学计算机科学与工程学院重庆 400054) (cz@cqut.edu.cn)

在信息化时代，终端设备的增加使物联网安全面临巨大挑战，特别是在军事、金融等安全性要求特别高的行业，身份认证是解决物联网安全问题的核心,而身份认证有待于解决的2个核心问题是密钥管理规模化和密钥分发.迄今为止，服务器在对终端身份认证主要存在下列3种方式:

1) 公钥基础设施(PKI).这是目前最广泛的认证方式，需要认证中心CA和大量数据库的支持，其中生成的密钥是随机产生的，用户名和密钥不存在线性关系，因此存在证书管理繁琐、数据库维护复杂、成本较高的问题，难以实现对密钥的规模化管理.

2) 基于身份的密码体制(IBE).主要的核心体制是用户名和密钥存在线性关系，通过身份标识直接进行认证，虽然在一定程度上解决了PKI认证过程中需要第三方的支持，但是需要保存用户参数，在密钥存储上需要提供额外的空间，虽然有统一的密钥管理系统，但是密钥分发存在缺点,成本性也比较高.

3) 组合公钥(CPK).是我国自主开发的算法认证过程中用户标识经过哈希函数、映射算法产生种子公私钥对，种子公钥经过组合运算产生密钥，认证时客户端保存公共用户参数，无需第三方CA的支持，实现了密钥的规模化管理和分发，在成本和实用上得到认可.因此，CPK成为我国独立进行技术研究的重点，并运用于大数据[1]、云计算[2-3]、身份认证[4-8]、防伪系统[9]等方面.

相比较PKI和IBE，CPK解决了PKI和IBE在认证过程中存在的问题，基于CPK本身的特性，认证过程在CPK芯片实现，客户端通过存储公钥因子经过组合运算生成大量的公钥对，效率高、安全性强、占用资源少.通过不断地改进，CPK的安全性得到不断完善和增强.但是在改进过程中发现CPK在密钥产生过程中会出现相同的身份，即密钥碰撞.产生密钥碰撞的原因是由下面2个环节引起的:1)用户标识经过哈希函数生成种子公私钥对(简称环节1)；2)种子密钥又经过ECC算法等产生标识密钥(简称环节2).因此发现一种有效解决密钥碰撞的方案成为了CPK完善和发展的浪潮.

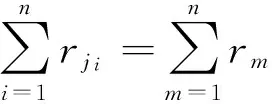
在文献[12]中，为了解决模“n”运算提出了约束椭圆曲线模“n”方案，即在环节2的过程中进行研究.该方案解决了在模“n”下的碰撞问题，但是在产生种子密钥对过程中无法解决经过哈希函数运算引起的碰撞.

文献[13]提出了一种新的方法来解决CPK的密钥碰撞问题.该方法提高密钥效率的原则是降低种子矩阵的规模化，解决了文献[12]中哈希运算可能产生的碰撞问题和文献[11]中模“n”运算出现的碰撞问题.但是映射识别过程中没有考虑到av=0(1≤v≤n)系数的情况.

文献[14]提出了映射方案去解决文献[13]中av=0(1≤v≤n)的情况.该方案通过缩小种子矩阵的公共参数有效地解决了椭圆曲线规模膨胀等问题，进一步提高了计算效率.但是，在标识映射环节降低了整体系统的安全性.

本文从用户标识经过哈希生成种子密钥矩阵和种子密钥矩阵产生标识密钥的环节出发，提出了一种双线性对方法，不仅解决了文献[11-12]提出的问题，而且通过离散对数降低椭圆曲线的规模，解决了文献[14]中安全性和无碰撞的比特流兼容性问题.

1 组合公钥(CPK)算法

荆海龙[15]提出了CPK可以通过有线域离散对数和椭圆曲线这2种方法构建.在相同的资源下，与有限域离散对数相比较，椭圆曲线的构建所需要的密钥矩阵在内存上更少，但在效率性上更高.因此，本文构建基于双线性对算法的椭圆曲线离散对解决CPK碰撞问题.

1.1 密钥矩阵的生成

椭圆曲线的参数T=(a,b,G,n,p)，其中，p为阶数，a,b∈Fp，G为基点，n为G上的阶.Ri,j(0≤i≤m,0≤j≤n)为PSK的元素，ri,j为SSK的元素，矩阵规模为m×n.

1) 构建的种子公钥矩阵PSK和种子私钥矩阵SSK如下：

其中，ri,j是Ri,j=(xi,j,yi,j)对于G的离散对数.显然，PSK与SSK这2个矩阵中任一对应位置上的元素Ri,j=(xi,j,yi,j)与ri,j形成一个公私钥对，故组合PSK中的倍点与SSK中的离散对数也可构成公私钥对.

2) 基于种子矩阵的密钥生成如下：

根据规则产生选取序列，在产生的序列之后，种子公钥矩阵与私钥矩阵根据该序列选取对应的位置上的元素来组合，这样可以产生一个实体的CPK公私钥对.

1.2 标识密钥的生成

利用CPK算法生成标识密钥的过程如图1所示，通过对身份标识进行哈希函数运算和ECC算法产生标识密钥.首先用户标识经过哈希函数运算和行映射算法生成种子矩阵，然后种子矩阵经过组合运算生成标识密钥.

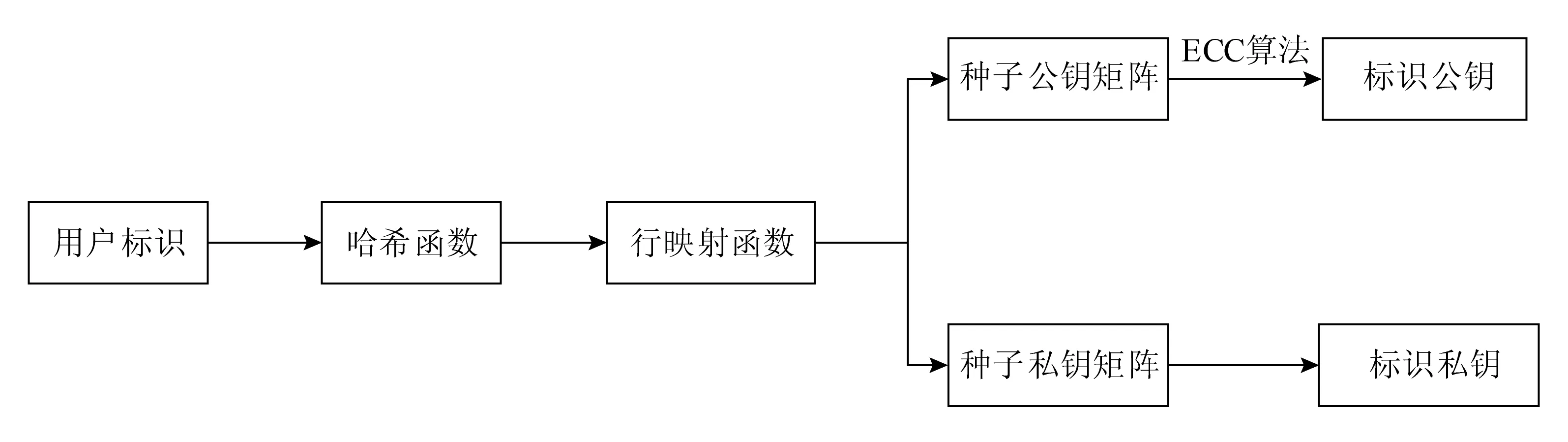
图1 标识密钥生成图

系数映射算法[14]通过从密钥生成和种子矩阵构建的环节出发,解决了文献[13]中av=0(1≤v≤n)的情况，降低了种子矩阵存储空间.但是在研究过程中发现存在比特流不兼容和安全隐患的问题，本文采用双线性对用户标识进行映射，解决了文献[11-12]的哈希函数运算引起的碰撞问题，同时，经过双曲线选取合适的G的取值解决了文献[14]中比特流产生过程中不安全性问题.

2 基于双线性对方法选取G值

2.1 G值的选取规则

选取G值的具体步骤如下：

步骤1. 选取G1和G2，定义双线性对:G1×G2→G3；

步骤2. 若len≤lenc，id先用比特0填充成lenc.设MP0=data1,MPi+1=E(MPi)(i≥0)，则计算行映射算法MP=E(id,key)；

步骤3. 若lenc≤lens则计算MPi+1=E(MPi,key)(0≤i≤lenc)；

步骤4. 通过行映射算法选取序列之后,选取一个合适的因子p(1≤p≤n)，根据y2G=(x3G+axG+b) modp和a+b=p2计算出合适G的取值；

步骤5. CPK密钥生成中心通过计算O=(h1(Z)⊕h2(Q))和key是否相等进一步来验证G取值的合理性.h1和h2是哈希函数运算，Z为椭圆曲线的主密钥，用户私钥为Q.

步骤6. 输出G值.

2.2 椭圆曲线的选取

在从上面G值的选取之中存在一个最大的因子p，其种子矩阵的长度为len+2p-3.满足椭圆曲线的五元组T=(a,b,G,n,p)中n的长度最少为len+2p-3，这样在任意的系数序列中可以避免模n运算而引起的碰撞.

3 无碰撞CPK方案的性能对比

至此，本文提出G值的取值方法上解决了安全性和比特流兼容性和安全问题.对本文提出的选取的方案与以前的方案进行对比，会发现在相同规模的需要下，种子矩阵密钥占用更少的空间，成本更低，而且不会发生用户标识相同情况下引起的碰撞问题.

假设矩阵的规模为m×n，每行av的长度为l，选取的G值的比特长度为Lr(av)=t.经过实验证明系统的安全性为1 024 b.

文献[11]中产生的密钥对数量为w=2n l，序列长度为nl(单位为b).种子矩阵的规模Nmax=nl(单位为kb)，椭圆曲线规模为256 b.矩阵的空间为M=nml.

文献[12]中产生的密钥对数量为w=2(t+l)n，序列长度为(t+l)n(单位为b).种子矩阵的规模Nmin=256 kb和Nmax=253+mn(t+2)(单位为kb)，椭圆曲线规模为255+mn(t+2)(单位为b).矩阵的空间为M=mnNmax.

本方案可产生的密钥对数量为w=2n(t+l)，序列长度为n(t+l)(单位为b).种子矩阵的规模Nmax=256 kb，椭圆曲线规模为1 024 b.矩阵的空间为M=mnNmax.

假设t=4,系统的安全需求为1 024 b,各种方案的性能对比如表1所示：

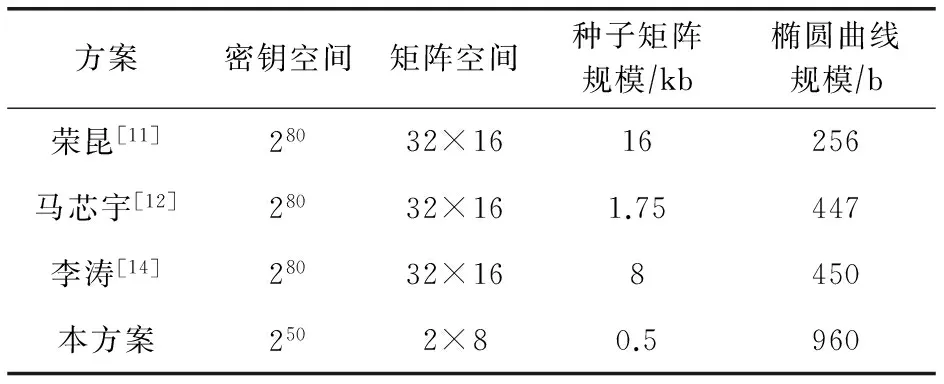
表1 各种方案的性能对比

4 安全性对比

本文在密钥产生过程中在椭圆曲线上选择合适的G点，然后根据G点进行相应的映射，与以前的CPK算法[14]相比较，没有在环节1过程中通过减少哈希函数运算来避免密钥的碰撞，也没有文献[13]在环节2过程中仅仅通过公钥进行对比来避免ECC算法.本方案通过选取合适的G值可以避免穷尽等一系列攻击.

5 结语

本文提出了一种基于双线性对方法建立的CPK方案，通过选取合适的G点不仅解决了系统的安全性和产生标识密钥过程中的碰撞问题，而且提高了CPK服务器对终端的认证效率，保密性极强，适用于政府和银行等保密性要求较高的行业.总体来说，公司的实验结果一致证明了本方案的安全性、通信性都具有优势，可以用于政府蓝牙耳机、保密箱的应用等.但是，由于本方案具有极强的加密性，导致在破解上可能无从下手，基于CPK的芯片是否能通过国家密码局的认可是下一步需要研究的重点.

[1]Chris V. A spatial distribution measure and collision analysis technique for distributed space systems[J]. Electronic Commerce Research, 2016, 32(8): 45-56

[2]田秀明. 基于CPK的Web服务认证系统的研究[D]. 天津: 天津大学, 2014

[3]李鹏程. 基于改进CPK的移动互联网身份认证方案研究与实现[D]. 南京: 南京邮电大学, 2016

[4]李涛. 基于CPK技术的无碰撞的多作用域身份认证算法的研究[D]. 北京: 中国科学院大学, 2015

[5]Feng Yu. Secure authentication scheme based on CPK[J]. Journal of Networks, 2010, 5(9): 1106-1113

[6]常晓林, 冯登国, 卿斯汉. 一次身份认证可访问多个应用服务器[J]. 软件学报, 2002, 13(6): 1111-1116

[7]马宇驰, 赵远, 邓依群, 等. 基于CPK的可信平台用户登录认证方案[J]. 计算机工程与应用, 2010, 46(1): 90-94

[8]孙伟达, 游向东. 一种基于CPK的移动终端加密系统[J]. 信息安全与通信保密, 2015, 37(12): 124-126

[9]Chen Y, Chou J S. ECC-based untraceable authentication for large-scale active-tag RFID systems[J]. Electronic Commerce Research, 2015, 15(1): 97-120

[10]王公浩, 王玟, 吴铎, 等. CPK随机碰撞概率分析[J]. 信息安全与通信保密, 2008, 30(11): 87-88

[11]荣昆, 李益发. CPK种子矩阵的优化设计方案[J]. 计算机工程与应用, 2006, 42(24): 120-121

[12]马芯宇, 龙翔, 范修斌. 无碰撞CPK的种子库构建和选取方案[J]. 计算机工程与应用, 2012, 48(27): 99-104, 113

[13]马安君, 李方伟, 朱江. 组合公钥体制的线性共谋攻击分析[J]. 计算机应用, 2013, 33(8): 2225-2227

[14]李涛, 张海英, 杨骏, 等. 无碰撞组合公钥的种子密钥矩阵的优化设计方案[J]. 计算机应用, 2015, 35(1): 83-87

[15]邢海龙. 组合公钥CPK关键技术研究与应用[D]. 长沙: 国防科学技术大学, 2009