基于改进CRO算法的Pareto多目标科学工作流调度算法

马敬敬，阎朝坤

(河南大学 计算机与信息工程学院，河南 开封 475000)

工作流作为一种面向过程建模和管理的核心技术，可以有效描述活动与活动间的复杂约束关系，已成为大规模科学应用的典型范式.采用科学工作流系统，将实现工作流程自动化，可以提高工作效率、减少浪费、提高利润、充分发挥现有计算机网络资源的作用.由于涉及大量的运算，为了提高工作效率、节省用户的时间、满足用户的QOS需求，就需要选择合适的调度策略进行任务和资源的分配.早期的科学工作流调度算法通常以执行时间和费用为用户的QOS指标，已存在一些使用智能算法进行网格计算任务调度问题的研究，如Song S[1]和林剑柠等人[2]采用遗传算法来求解网格计算任务调度问题，季一木和王汝传[3]提出了基于粒子群的网格任务调度算法，Izakian等[4]利用PSO算法求解网格任务调度.工作流调度算法[5-6]在日常生活中应用越来越广泛，随着互联网络在不断地发展，网络的开放性也使得网络的安全问题越来越突出，因此用户将更多地关注在分布式计算环境中任务执行的安全性问题，为了使用户使用虚拟资源更加放心，并且使任务调度系统运行地更加高效，服务商就需要进行多目标优化调度，找到最优解决方案.通过对多目标进行优化可以降低能耗，提高系统效率.针对传统的科学工作流调度算法忽略了在分布式云环境[7]中的安全问题，笔者对化学反应优化算法进行了改进并应用于以执行时间、安全性为目标的多目标工作流调度问题中，采用Pareto机制的多目标优化技术，提出了一种多目标工作流调度算法MOCRO[8]，基于工作流仿真模拟器Workflowsim的实验结果表明，相对于MOGA[9]、MOPSO算法[10]，提出的MOCRO算法具有一定的优越性.

1　多目标化学反应算法 MOCRO

这里介绍一种基于CRO算法的Pareto多目标科学工作流调度算法[11].任务的完成时间(makespan)，即工作流中出口任务的运行结束时间.makespan表明了工作流调度的效率，其值越小，说明任务完成越快,调度的效率就较高.信任度(trust)从两个方面有所表现：一个是任务调度的安全性，从任务的真实性、保密性和完整性这三个角度衡量；另一个则是资源的可靠性，表征一组工作流在虚拟资源上执行后对于用户来说是否可靠，这两个属性综合在一起便是工作流调度的信任问题.CRO作为一种新的智能搜索算法应用在多目标优化问题上，笔者提出了基于改进CRO算法的多目标工作流调度算法.

1.1　系统模型定义

1.1.1工作流模型

一个科学工作流可以用DAG来描述，即为G= {V,E}，图中的节点集合V= {T1,T2,...,Tn}代表了工作流中的每一个任务，其中n是任务的数量，图中的边集合E则代表了任务之间的约束关系[8].对于DAG图中的一条边dij= (Ti,Tj)∈E,其中任务i称为任务j的父任务，任务j为任务i的子任务，该式表明了两个任务的调度顺序，即只有在任务i成功执行后任务j才能开始调度.

在进行优化工作流的makespan时，每一个任务Ti∈V都有着自己的任务负载(workload)：

T= {t1,t2,...,tn}

(1)

Workload= {wl1,wl2,...,wln}

(2)

其中，ti为第i个任务，wi为第i个任务的任务负载，n为任务的编号.

1.1.2任务模型

因为需要考虑任务的信任属性，所以每一个任务还会包括任务安全性需求、任务可靠性需求.对于一个工作流中的任务可以用以下公式来表示.

TaskSecurityRequirements= {ts1,ts2,...,tsn}

(3)

TaskReliabilityRequirement= {tr1,tr2,...,trn}

(4)

1.1.3资源模型

同样对每一个资源来说也需要从两个方面考虑信任属性.因此，资源还会提供资源的安全性和资源的可靠性.而资源的可靠性是要由任务和资源共同决定的，在调度前，每个资源都有着自己的资源固有失效率，伴随时间的增长资源失效的概率便会渐渐增加，那么该资源的可靠性也就会降低.则对一个虚拟资源可以用以下公式来表示.

Vm= {vm1,vm2,...,vmm}

(5)

Mips= {mips1,mips2,...,mipsm}

(6)

ResourceSecurity= {rs1,rs2,...,rsm}

(7)

ResourceReliability= {rr1,rr2,...,rrm}

(8)

FailureRate= {fr1,fr2,...,frm}

(9)

另外对于任务i及资源j来说，它们资源的可靠性RRij计算如公式10.

rrij= exp(-ECTij×frj)

(10)

其中exp()表示以自然常数e为底的指数函数，ECTij表示任务i在资源j上的完成时间.

1.1.4信任模型

任务和资源间的信任关系可以分为三种：强信任关系(strong trust relationship)、弱信任关系(weak trust relationship)和无信任关系(no trust relationship)[12].根据这三种信任关系，任务i在资源j上进行调度时安全性值的计算如下所示：

(11)

secValueweak(i,j)=

(12)

secValueno(i,j)=tsi/maxLevel

(13)

同样，对于调度时可靠性值的计算如下所示：

(14)

reliValueweak(i,j)=

(15)

reliValueno(i,j)=(1-exp(-rrij))/(1-exp(-1))

(16)

则任务i在资源上调度时所得到的信任值可以用公式17表示，

trustValue(i,j)=α×secValue(i,j)+β×reliValue(i,j),α+β=1

(17)

其中α,β是安全性和可靠性的权值，其值越大，说明对用户来说就更加重要，在本文中默认设置α,β值均为0.5.

1.2　多目标调度问题定义

信任函数值越大表明了任务调度成功后就越稳定，其执行的结果也更加可信.多目标工作流调度模型可以用公式18和19来描述：

Minimizemakespan=FinishTime(Texit)

(18)

Maximizetrust=TrustValue(Solution)

(19)

科学工作流调度时间优化的问题就是将所有任务分配到合适的虚拟资源上使整体的任务完成时间最小.而最后一个任务，即出口任务的完成时间便是优化的目标完成时间.因此，对完成时间的优化调度问题便可以表示为：

Minimizemakespan=FinishTime(Texit)

(20)

2　Pareto最优解集介绍

在目标调度问题中，每一种解决方案都拥有不少于一个的目标值，不能获得一个最优解使多个目标值同时达到最优，此时就需要获得一个最优解集.对于解集中的每一个解决方案来说，它们之间各自有自己的优势.解决多目标调度问题，常见的解决方案有两种：第一种是使用线性加权的方式，将多个目标通过目标权重简化为单目标问题.这种方案折中的方法虽能从一定程度上解决工作流调度问题，但是其结果不一定满足用户的需求，因为对于用户来说，会根据实际情况选择调度方案.所以就需要采取第二种方法,该方法是以通过智能算法进行Pareto集的优化，该集合中的每一个解之间不存在优劣性，他们互为非劣性，用户根据调度结果偏好于自己的解决方案.

2.1　Pareto相关概念

首先依据多个目标值的最小化问题，先了解Pareto的相关概念：

(1)优劣性：有两个解X，Y，若解X中的所有目标值都小于解Y的目标值，那么就认为X优于Y，或者说Y劣于X.

(2)非劣性：对于解X，Y，若X既不优于Y也不劣于Y，则称两者互为非劣，这种非劣性也称为Pareto性.

(3)Pareto最优解集：解集中的所有解都具有非劣性.

2.2　Pareto最优解集实现方法

笔者将采用Pareto排序赋值的方法解决多目标优化调度问题[13].对于种群中的每一个个体都拥有多个目标值，若一个个体不劣于种群中的其他任何一个个体，那么该个体的排序值为1，也既是一个Pareto最优解.而若一个个体在种群中存在其他个体优于它，那么每存在一个优于它的个体，它的排序值便依次加1，同时由于存在其他个体优于该个体，所以该个体最后会被移除.这样不断进行个体的Pareto排序赋值直到所有个体结束，那个排序值为1的个体也便组成了Pareto最优解集.如下图图1所示，排序值为1的个体优于排序值为2的个体.

图1　以多目标最小化问题描绘排序赋值图

3　实验分析

实验在AMD 4.00 G， 64 G系统上基于WorkflowSim进行了仿真实验，模拟了5个虚拟资源，分别选取了三种不同的任务数50，100和1 000对两种典型的科学工作流模型Inspiral和Montage进行了测试.实验中的具体参数设置和结果分析详情如下.

3.1　主要参数设置

3.1.1仿真系统参数设置

虚拟资源的数量为5，每个资源的计算能力在400～1 200之间取值，任务与虚拟资源的信任关系的确定方法是通过生成一个处于[0,1]之间的随机数，若该随机数小于0.25,则表明两者间的信任关系较强，若该随机数大于0.25小于0.5，则说明两者间的信任关系较弱，否则就是两者间无信任关系.

任务的安全性需求和虚拟资源的安全性是处于[0,1]间的随机数，资源固有失效率初始化为[0.000 1, 0.001 5]的随机数，而任务的可靠性需求则需要根据公式21来计算得到.

tr=(0.9+0.1×γ)×exp{10-4×(NumofTask/NumofVm)}

(21)

其中γ表示[0, 1]之间的随机数.

3.1.2算法参数设置

实验分别针对三种多目标智能算法MOCRO，MOGA和MOPSO进行仿真，具体的参数设置如表1所示.

3.2　仿真结果及实验分析

通过三种算法对不同的任务量进行实验分析，实验主要对工作流调度的效率(makespan)以及信任度(trust)的结果进行了分析从而获得多目标化学反应算法MOCRO最优的Pareto解集.

表1　智能算法参数设置情况表

表2、表3、表4记录了在Montage和Inspiral下任务量分别为50,100和1 000各算法收敛时的Makespan和trust值.

表2　Montage_50和Inspiral_50

表3　Montage_100和Inspiral_100收敛时的

从表2到表4可以看出，较其他两种算法在两种工作流调度下MOCRO的优化效果要好.例如，在Montage工作流调度下任务数量为1 000时，MOCRO收敛时的完成时间为3 945.887 1信任度为843.094 79，MOGA的完成时间为5 094.633 32信任度为832.402 83，MOPSO的完成时间为4 424.653 92信任度为837.878 47，相比较可以看出算法MOCRO用时最少且信任度也是最好的.

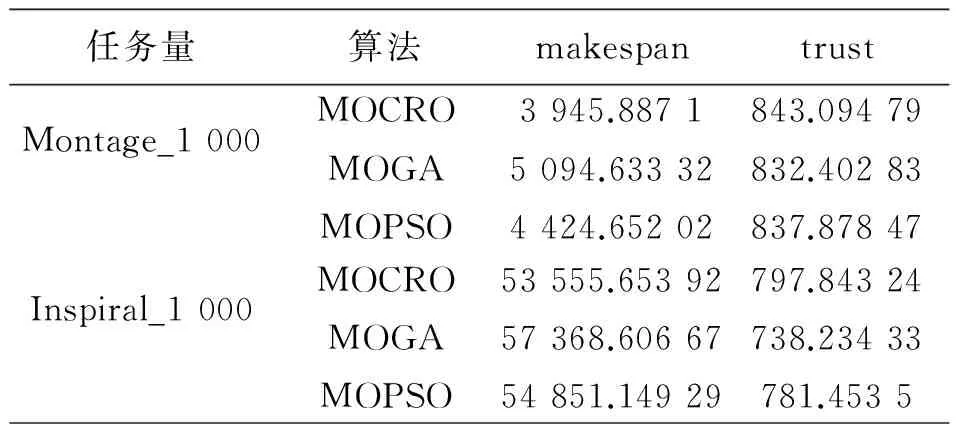
表4　Montage_1000和Inspiral_1000

图2　在二维坐标系下Pareto最优解集分布图

从图2可以看出，MOCRO的Pareto最优解集中分布在makespan为(300,420)，MOPSO的Pareto最优解集中分布在makespan为(450,520)，MOGA的Pareto最优解集中分布在makespan为(470,570),MOCRO相比较MOGA和MOPSO优化性能较好.

4　小结

笔者考虑到任务与资源间的信任关系以及资源的损失效率，为了使用户使用虚拟资源更加放心，并且使任务调度系统运行更加高效，服务商就需要进行多目标优化调度，提出一种新的信任度量化任务在资源上执行的安全性.因此，CRO被用于找到最优解决方案，通过对多目标进行优化可以降低能耗，提高系统效率.

通过对五个虚拟资源进行模拟，同时选取三个不同的任务数进行实验分析，实验结果表明MOCRO相比其他两种算法MOGA和MOPSO的任务完成时间(makespan)较小,说明该算法的工作流调度的效率最高任务完成最快.同时相比其他两种算法信任度(trust)最大即任务调度的安全性和资源的可靠性最高.笔者的实验进一步验证了CRO算法在多目标优化问题取得不错的效果.未来将继续研究CRO的改进及其在不同领域问题的应用，将CRO与其他进化算法如ACO[14]、FES、PSO[15]等相结合，根据不同问题提出相应的改进算法是CRO的热点.

参考文献：

[1]Song S, Kai H, Kwok Y K. Risk-resilient heuristics and genetic algorithms for security-assured grid jobscheduling[J]. IEEE Transactions on Computers, 2006, 55(6):703-719.

[2]林剑柠, 吴慧中. 基于遗传算法的网格资源调度算法[J]. 计算机研究与发展, 2004, 41(12):2195-2199.

[3]季一木, 王汝传. 基于粒子群的网格任务调度算法研究[J]. 通信学报, 2007, 28(10):60-66.

[4]Izakian H, Ladani B T, Zamanifar K, et al. A Novel Particle Swarm Optimization Approach for Grid Job Scheduling[J]. Communications in Computer & Information Science, 2010, 31(9):100-109.

[5]陈爱国, 王玲, 任金胜, 等. 基于资源分组的多约束云工作流调度算法[J]. 电子科技大学学报, 2017, 46(3): 562-568.

[6]杨光, 郭生练, 陈柯兵, 等. 基于决策因子选择的梯级水库多目标优化调度规则研究[J]. 水利学报, 2017, 48(8): 914-923.

[7]余盛季, 魏恺明, 李强, 等. 云计算环境下基于时间和可靠性的调度策略[J]. 计算机应用研究, 2016, 33(9): 2673-2678.

[8]Marzouki B, Driss O B, Ghédira K. Multi Agent model based on Chemical Reaction Optimization with Greedy algorithm for Flexible Job shop Scheduling Problem[J]. Procedia Computer Science, 2017, 112: 81-90.

[9]Schwartz Y,Raslan R, Mumovic D. Implementing multi objective genetic algorithm for life cycle carbon footprint and life cycle cost minimisation: A building refurbishment case study[J]. Energy, 2016, 97: 58-68.

[10]陈进, 郭小锋, 孙振业, 等. 基于改进多目标粒子群算法的风力机大厚度翼型优化设计[J]. 东北大学学报 (自然科学版), 2016, 37(2): 232-236.

[11]Rodriguez M A,Buyya R. Deadline Based Resource Provisioningand Scheduling Algorithm for Scientific Workflows on Clouds[J]. Cloud Computing IEEE Transactions on, 2014, 2(2):222-235.

[12]Gupta H,Vahid Dastjerdi A, Ghosh S K, et al. iFogSim: A toolkit for modeling and simulation of resource management techniques in the Internet of Things, Edge and Fog computing environments[J]. Software: Practice and Experience, 2017, 47(9): 1275-1296.

[13]Durillo J J, Nae V, Prodan R. Multi-objective energy-efficient workflow scheduling using list-based heuristics[J]. Future Generation Computer Systems, 2014, 36(3):221-236.

[14]Chen W N, Zhang J. An Ant Colony Optimization Approach to a Grid Workflow Scheduling Problem With Various QoS Requirements[J]. IEEE Transactions on Systems Man & Cybernetics Part C, 2009, 39(1):29-43.

[15]张超, 李擎, 王伟乾, 等. 基于自适应搜索的免疫粒子群算法[J]. 工程科学学报, 2017, 39(1): 125-132.