基于复瞄的某火箭炮位置伺服系统研究

蒋梦琴，高　强，侯远龙，刘静宝，曾令梦

(南京理工大学 机械工程学院，江苏 南京　210094)

火箭炮是一种威力大、火力猛、机动性强的高性能武器系统，可在短时间内发射大量的火箭弹，用以歼灭、压制敌方有生力量和技术兵器[1]。而火箭炮伺服系统是一个复杂的非线性系统，在发射过程中伴随着火箭炮系统转动惯量的变化，系统刚度、阻尼的变化，系统参数的较大变化导致系统模型变化[2]；在发射状态时系统受连续燃气流冲击力矩等强干扰导致炮弹的发射平台振动[3-4]，偏离了初始位置，使得后续射弹在此发射环境下命中精度降低[5-6]。故研究基于复瞄的火箭炮伺服系统，在火箭炮每发射一次后，进行复瞄工作，旨在进一步提高火箭炮的复瞄速度与精度。

传统控制方式已难以满足火箭炮系统的发射精度要求。近年来，自抗扰控制理论因其较好的工程应用背景，被广泛应用到电力系统、武器系统等领域[7]。文献[8]针对无人机飞行过程中受到的各类干扰源问题，采用了自抗扰控制方法，改善无人机的稳定性；文献[9]将自抗扰控制理论应用于PMSM调速系统中，并简化了自抗扰控制器，结构更简单；文献[10]针对运动平台需要强抗扰动和快速跟踪的要求，设计了稳定平台的自抗扰控制器，提高了系统性能。

笔者针对火箭炮在发射状态时存在燃气流冲击力矩等强干扰，设计了非线性扩张状态观测器对系统的未知扰动进行估计并做相应的补偿，并设计了相应的非线性PID反馈控制律。仿真结果表明，该方法减弱了燃气流等强干扰对系统精度的影响，提高了火箭炮的复瞄速度与精度。

1　系统建模

火箭炮位置伺服系统由位置控制器、PMSM、减速器、驱动器以及位置信号反馈等构成，可分为俯仰和方位伺服系统，结构图如图1所示。笔者针对方位伺服系统进行研究。

1.1　永磁同步电机数学模型

PMSM是具有非线性、强耦合的动态系统，为使电机具有好的控制特性，采用矢量变换进行线性解耦控制。为了简化分析，作如下假设[11]：

1)忽略铁芯的饱和效应。

2)气隙磁场呈正弦分布。

3)不计涡流和磁带损耗。

4)转子上无阻尼绕组，永磁体也没有阻尼作用。

5)采用id=0的矢量控制方法。

以表面式永磁同步电机为例，它是凸极式永磁同步电机的特例，满足Ld=Lq=L。可得在dq坐标系下，其线性化数学模型为：

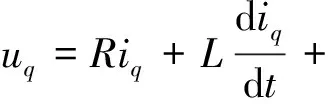
(1)

ud=-ωeLiq

(2)

Te=1.5pnψfiq=Ktiq

(3)

机械运动方程为

(4)

式中：ud与uq分别为d、q轴的电枢电压分量；iq与L分别为q轴的电枢电流分量、等效电枢电感；R与ωe(=pnωm)分别为电枢绕组电阻和电角速度；ψf与pn分别为永磁铁对应的转子磁链和电机的极对数；Te与TL分别为电机的电磁转矩和系统等效到电机轴的负载力矩；B与J分别为系统粘滞摩擦系数和等效转动惯量；Kt为电磁转矩系数。

1.2　火箭炮伺服系统模型

火箭炮位置伺服系统常采用电流环、速度环和位置环的三闭环系统；实际中的电机驱动器多数固化有电流控制器和速度控制器，故笔者选择的驱动器内部配置有电流环和速度环，则以驱动器的输入端即输入角速度ωr为控制量u，减速器输出端角位置θa为系统输出量，系统模型建立如图2所示。

图2中，Gω为速度控制器，Gi为电流环控制参数，KE(=Kt/1.5)为电势系数，Kv为速度反馈系数，i为减速比，ωa为减速器输出端角速度，θa为减速器输出端角位置。在实际系统中，TL不仅包括作用在电机轴的负载力矩，还包括外部干扰所引起的转矩波动等。

考虑到电磁时间常数比机械时间常数小很多，且电流环速度远快于速度环和位置环的响应速度，故可将电流环近似简化为比例系数为1的比例环节。将速度环简化为P控制，比例系数记为Kω，则系统模型可简化,如图3所示。

由此可得速度环和电流环简化后的经典二阶模型为

(5)

本文只考虑位置环设计，速度环和电流环采用的是传统的PID控制方式，不作深入研究。

以火箭炮方位伺服系统为研究对象，转角范围为-110°～110°，系统参数如表1所示。

表1　火箭炮方位伺服系统参数

2　自抗扰控制器设计

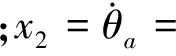
由式(5)可得，系统状态空间方程为

(6)

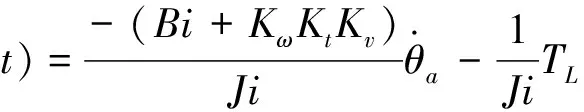
则将式(6)扩张为

(7)

式中:x3=f(x1,x2,w(t),t)为扩张的状态，即系统未知部分；h(x1,x2,w(t),t)为未知部分的微分。

二阶ADRC控制器结构图如图4所示。按此结构图设计ADRC控制器。

2.1　跟踪微分器TD

TD为参考输入安排过渡过程，减少系统的初始误差，解决系统响应快速性和超调性之间的矛盾。这里采用文献[12]提出的一种非线性微分跟踪器STD。它具有形式简单、调参容易的优点，形式为

(8)

式中：v为输入信号，即给定的位置信号θr；v1为给定位置的跟踪信号；v2为给定位置跟踪信号的微分信号；R为速度因子，适当增大R，可以加快跟踪速度；sigmoid函数为激励函数，采用改进的sigmoid函数，形式为

sig(x;a,b)=a[(1+e-bx)-1-0.5]

(9)

式中：a是幅值增益，可以调整sig(x)的幅值；b是指数因子，用来调整函数的近似线性工作区间的范围。

2.2　扩张状态观测器ESO

由式(7)，设计得到火箭炮伺服系统三阶扩张状态观测器：

(10)

式中：z1为减速器输出端角位置估计值，即负载角位置估计值；z2为减速器输出端角速度估计值，即负载角速度估计值；z3为扩张状态估计值，这里包括状态变量和外部负载扰动估计；e为观测角位置与实际输出角位置的误差；β1～β3为观测器的增益；α1,α2为fal函数的参数；δ为fal函数线性段的区间长度；b0为控制增益b的估计值。

函数fal(e,α,δ)定义为：

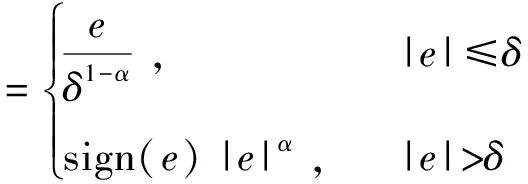
(11)

式中，sign函数为符号函数。

2.3　状态误差反馈律

u0=k1fal(e1,α3,δ)+k2fal(e2,α4,δ)

(12)

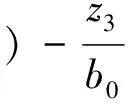
(13)

3　仿真分析

利用某火箭炮方位伺服系统的数学模型为研究对象，通过Matlab/Simulink软件搭建系统控制模型，进行计算机仿真来验证所提出控制器的有效性。

控制器的参数设计如下：

TD的参数，R=30,a1=5，a2=0.5，b1=2，b2=0.5。

ESO的参数，β1=100，β2=350，β3=1 100，α1=0.5，α2=0.25，δ=0.025。

PID的参数，k1=20，k2=11.9，α3=3/4，α4=2.45/2，δ=0.02，b0=25.1。

3.1　正弦跟踪仿真

仿真输入设为θr=0.75sin 0.3πt，rad；外部干扰设为d(t)=2sin2t+3，仿真时间10 s。假设正弦跟踪时，火箭炮发射弹量不变。仿真试验设计为2种控制方法的对比，即常规PID控制和自抗扰控制(ADRC)，比较其位置跟踪性能。

2.3 心肌免疫组织化学染色结果 Bmal1：糖尿病ZT23亚组在细胞膜、胞质中呈棕黄色表达；糖尿病ZT23亚组大鼠心肌染色呈黄褐色，在细胞质、细胞膜内均有表达(图2a、2b)；Per2：非糖尿病ZT23亚组细胞质淡黄色，呈微弱的阳性；糖尿病ZT23亚组心肌染色均呈黄褐色，细胞质、细胞膜内均有表达(图2c、2d)。

正弦输入下的仿真组图和观测误差图如图5～6所示。

从仿真图5中可以看出，达到稳定跟踪的状态以后，采用PID控制策略的误差最大，在仿真的整个过程中也存在1.76 mrad的位置跟踪动态误差，控制效果一般。而采用(ADRC)控制，动态跟踪误差为0.26 mrad，控制效果良好。从图6(a)看出稳定后角度观测误差最大为0.008 1 mrad，观测效果良好；图6(b) 看出稳定后角速度观测误差最大为6.2 mrad/s，观测效果良好。

3.2　燃气流冲击仿真

阶跃输入θr=0.17 rad，即调炮到10°位置。实际系统中，5 s后每隔1 s发射1次。数字仿真中，只模拟一次发射，在仿真5 s时给负载力矩加上一个强干扰信号，来模拟燃气流冲击力矩；因只模拟一次发射，故不考虑发射弹量减少引起的负载转矩变化。该信号设为持续0.2 s的幅值为80 N·m的方波干扰，其余负载干扰为d(t)=5sin 3t，如图7所示。图7中的观测干扰曲线即z3，包括状态变量和外部负载扰动估计，而实际干扰曲线的构成为外部干扰值，不考虑影响较小的状态变量的观测值。

从图7看出观测器对干扰的估计在开始0.9 s内有较大误差，之后观测效果良好，且在5 s处对强干扰的估计效果良好，但之后的调整时间较长，有待进一步完善控制参数的整定。

燃气流冲击仿真图和观测器观测曲线如图8～9所示。

从图8中可以看出，采用ADRC控制，稳定地跟踪上输入所用的时间在1 s左右；达到稳定跟踪的状态以后，系统在5.0 ～ 5.2 s的强干扰力矩下，输出角度误差最大为3 mrad，并能在600 ms左右时间内返回初始位置，保证了后续射弹的命中率。从图8(b)看出采用PID控制策略，在小干扰下误差较小，但在5 s处的强干扰下误差较大，达到20 mrad，且调整时间较长。

从图9(a)看出在强干扰处的角度观测误差最大为0.047 mrad，观测效果良好；图9(b)看出观测器对角速度的观测在开始0.9 s内有较大误差，在强干扰处的角速度观测误差最大为49 mrad/s，其余观测效果良好。

4　结论

笔者针对火箭炮在发射状态时存在燃气流冲击力矩等强干扰，使得火箭炮炮管发射后偏离初始位置的问题，提出了基于复瞄的火箭炮伺服系统控制。运用自抗扰理论，设计了非线性扩张状态观测器对系统的未知扰动进行估计并做出相应的补偿，来减弱燃气流等强干扰对火箭炮发射精度的影响，提高了火箭炮的复瞄速度与精度；选择了一种改进的非线性微分跟踪器STD，具有形式简单、调参容易的优点；控制律选择非线性PID反馈控制率，提高了效率。数字仿真结果表明，系统在燃气流冲击等干扰下能够在规定时间内返回初始位置，保证后续射弹的命中精度，证明了该方法的有效性。

参考文献(References)

[1] 张敬.火箭炮的发展及性能提高的途径[J]．导弹与航天运载技术，2001(2)：58-61.

ZHANG Jing. The development of rockets and the ways to improve the performance of rockets[J]. Missile and Space Launch Technology, 2001(2)：58-61.(in Chinese)

[2] HU Jian, MA Dawei, GUO Yajun, et.al. Optimal PID position controller of multi-rocket launcher using improved Elman network[C]∥Proceeding of the 8th World Congress on Intelligent Control and Automation.Jinan, China: IEEE,2010:2424-2429.

[3] 刘协权,李世恒.火箭炮定向管平行度测量研究[J].测试技术学报,2002,16(增刊1)：141-144.

LIU Xiequan, LI Shiheng. Research on parallelism mea-surement of rocket launcher directional tube[J]. Journal of Testing Technology, 2002,16(Sup1):141-144. (in Chinese)

[4] 郑颖,马大为,姚建勇,等.火箭炮位置伺服系统自抗扰控制[J].兵工学报,2014,35(5):597-603.

ZHENG Ying, MA Dawei, YAO Jianyong, et al. Active disturbance rejection control for position servo system of rocket launcher[J]. Acta Armamentarii, 2014,35(5):597-603. (in Chinese)

[5] 张世强.某武器系统平行度校准装置的控制系统设计[D].哈尔滨：哈尔滨工业大学,2011:8-9.

ZHANG Shiqiang. Design of control system of a weapon system parallel calibration device[D]. Harbin: Harbin Institute of Technology, 2011:8-9. (in Chinese)

[6] 宋岩峰,邵晓鹏,朱新宏.多管航空火箭发射器激光校靶系统[J].电光与控制,2008,15(4):81-84.

SONG Yanfeng, SHAO Xiaopeng, ZHU Xinhong. Multi-tube rocket launcher laser calibration target system[J]. Elec-lightning and Control, 2008,15(4):81-84. (in Chinese)

[7] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.

HAN Jingqing. Active disturbance rejection control technology[M]. Beijing: National Defense Industry Press, 2008. (in Chinese)

[8] 曹宇.无人机非线性自抗扰控制方法研究[D]. 哈尔滨：哈尔滨工业大学,2013:6-7.

CAO Yu. Research of nonlinear active disturbance rejection control with application to unmanned aerial vehicle[D]. Harbin: Harbin Institute of Technology, 2013:6-7. (in Chinese)

[9] 焦姣姣,张兴华.永磁同步电机调速系统的自抗扰控制器设计[J].微电机,2015，48(11):77-80.

JIAO Jiaojiao, ZHANG Xinghua. Design of ADRC in PMSM speed control system[J]. Micro Motor, 2015，48(11):77-80. (in Chinese)

[10] 李锦英,付承毓,唐涛，等.运动平台上光电跟踪系统的自抗扰控制器设计[J].控制理论与应用,2012，29(7): 955-958.

LI Jinying, FU Chengyu, TANG Tao, et al. Design of active disturbance rejection controller for photoelectric tracking system on moving bed[J]. Control Theory & Application, 2012，29 (7) : 955-958. (in Chinese)

[11] 陈才学.基于观测器的永磁同步电机鲁棒稳定性分析与控制器设计[D].广州:华南理工大学,2014:18.

CHEN Caixue. Robust stability analysis of permanent magnet synchronous motor and controller design based on observer[D]. Guangzhou: South China University of Technology, 2014:18. (in Chinese)

[12] 邵星灵,王宏伦. 基于改进sigmoid函数的非线性跟踪微分器[J]. 控制理论与应用,2014，31(8):1117- 1122.

SHAO Xingling, WANG Honglun. Nonlinear tracking differentiator based on improved sigmoid function[J]. Control Theory & Application, 2014，31(8):1117-1122. (in Chinese)