总体最小二乘平差理论解算方法对比分析

姜家庆＊

（天津市市政工程设计研究院，天津 300202）

0　引言

在数据处理中，最小二乘法（Least Squares,LS）是最基本的数据处理方法，从18世纪高斯提出后发展至今成为数据处理领域应用最广泛的方法。最小二乘法是以只存在观测向量误差为前提的。然而，在测量数据处理过程中，由于采样误差和建模误差，观测向量误差和系数矩阵偏差往往是同时存在的。在这种情况下，用最小二乘法求得的参数估值就不再是最优无偏估计了。针对这种情况，在20世纪80年代有学者对最小二乘方法进行扩展，提出了总体最小二乘方法，该方法在计算观测值误差的同时还能顾及模型系数矩阵误差，在系数矩阵存在误差时，总体最小二乘解比最小二乘解更为真实可靠。

在本章节中，作者首先以一个直线拟合模型介绍最小二乘方法的基本思想及原理；然后以一个系数矩阵存在误差的问题引出总体最小二乘方法并阐述了其原理；最后给出了两种最为常见的总体最小二乘问题的解法及其详细的推导过程。

1　总体最小二乘原理及解法

经典的高斯-马尔柯夫模型假设函数模型是已知且非随机的，并且只考虑观测向量含随机误差，假设系数矩阵不存在误差或者不考虑系数矩阵误差。但是在很多实际问题中，比如大地测量反演、边坡监测、空间数据分析和坐标转换等数学模型中，函数模型的系数矩阵也是由观测数据组成。因此，不仅观测向量存在误差，系数矩阵也有可能出现随机误差。此时，再用最小二乘原理做数据处理的话，计算结果就不能再保证其最优无偏性。而总体最小二乘方法就能很好地解决这一问题，该方法在计算观测值误差的同时还能顾及模型系数矩阵误差。

1.1　总体最小二乘问题描述

设线性函数模型为：L=AX-V （1）

上式中，L为 n×1观测向量，A为 n×t系数矩阵，X为 t×1未知参数，V为观测向量误差。总体最小二乘方法是不仅考虑观测向量含有误差V，而且还顾及系数矩阵误差EA，那么上式应改写为

对应的误差方程可写为

误差的期望和方差为

式中，In和 It分别为 n和 t阶单位矩阵，vec(EA)是将 矩 阵 EA按列拉直得到的列向 量化函 数，vec(EA)∈R(n×t)×1；表示克罗内克(Kronecker)积。（2-10）式的矩阵形式为

求解上述方程的总体最小二乘方法可以表示为一个约束化问题：

求解‖(EA,V)‖F最小的问题即为总体最小二乘问题，当n＜t+1即方程个数小于未知参数个数时，存在无数多个解X，用总体最小二乘解可以给出其最小范数解。而总体最小二乘问题主要是研究当n＞t即线性方程超定时的总体最小二乘解。下面就介绍一下超定方程的两种常用的总体最小二乘解法。

1.2　总体最小二乘的奇异值分解法

奇异值分解是线性代数中一种非常重要的矩阵分解方法，最早由Golub和Van Loan引入求解总体最小二乘问题。

一般情况下，求解线性方程L=AX，当n≥t+1时，NTN的阶数小于或等于 NNT，此时，由矩阵 NTN求出来的最小特征值对应的特征向量就是对应于最小奇异∑t+1值的右奇异向量Wt+1。将

代入式（2-24），该式可变换为

则有

1）列观测方程，建立函数模型 L+V=(A+EA)X；

2）构建增广矩阵 N=[A L]，并对增广矩阵进行奇异值分解；

3）求解矩阵 NTN的特征值，并得出最小特征值 σt+1；

1.3　总体最小二乘的迭代解法

Schaffrin和鲁铁定等对总体最小二乘平差模型和推到方法进行了改进后[97、98]，得出总体最小二乘平差准则为

以式（2-10）为条件，按拉格朗日乘数法求解，构成目标函数为

由式（12）和（13）分别可得

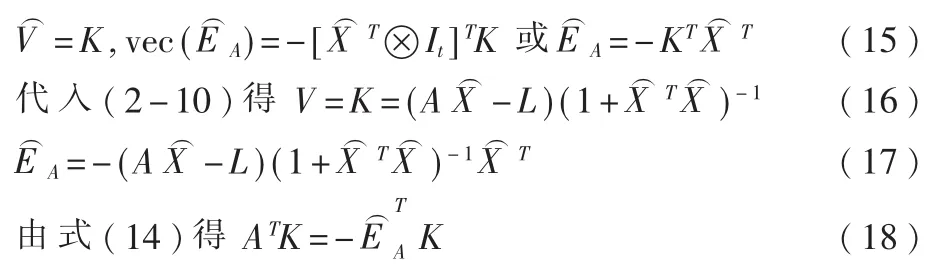
将式（16）代入上式，可得

将（20）式化为

同时

将（21）和（22）写成矩阵形式

上式即为参数的总体最小二乘解，采用迭代求解。

2　两种求解方法比较分析

总体最小二乘的奇异值分解法是基于数值逼近理论的总体最小二乘解，该解法没有顾忌变量误差（EIV）的随机模型，因此总体最小二乘的奇异值分解法求得的参数估值并不是真正统计意义上的TLS解。奇异值分解法无法获得相关情况下的平差模型以及观测数据不等精度的统计意义上的最佳估值，而这种情况在大地测量领域又是普遍存在的。因此，尽管奇异值分解法算法简单，其在大地测量领域的应用也受到了很多的限制。

总体最小二乘的迭代解法是Schaffrin等人基于拉格朗日求极值并且结合测量数据处理的特点，从测量平差的角度，顾及系数矩阵含有误差的情况下，构建拉格朗日条件极值的目标函数，并推导出来的总体最小二乘解法。

从理论上来讲，在观测量独立等精度的情况下，两种解法是等价的。然而在测量数据处理过程中，往往是出现观测量精度不等的情况。总体最小二乘的迭代解法是从测量平差的角度推导而来的，因此该算法更适用于测量数据处理。

3　结论

最小二乘法是测绘数据处理领域中最基本的数据处理方法，但是最小二乘方法有很大局限性，即最小二乘只考虑观测向量的误差而不考虑系数矩阵的误差或者是假设系数矩阵不存在误差。然而，在实际的数据处理过程中发现，观测方程系数矩阵往往会存在一定的偏差。如果直接忽略观测系数矩阵偏差的影响，求得的参数估值必然不是最优无偏估计。总体最小二乘方法的提出则很好的解决了这一问题，该方法在考虑观测向量误差的同时也顾及了观测方程系数矩阵偏差。当观测方程系数矩阵存在偏差时，总体最小二乘解比最小二乘解更为真实可靠。在求解总体最小二乘问题时，最常用的方法有奇异值分解法和迭代解法。由于在测量数据处理过程中，观测向量往往是精度不相等的，总体最小二乘的迭代解法更适用于测量数据处理。

【参考文献】

［1］陶武勇,鲁铁定.基于奇异值分解法的抗差总体最小二乘[J].江 西 科 学 ,2015,33(01)：101-105.

［2］鲁铁定,周世健.总体最小二乘的迭代解法[J].武汉大学学 报 (信 息 科 学 版 ),2010,35(11)：1351-1354.

［3］王乐洋.测边网坐标的总体最小二乘平差方法[J].大地测量与地球动力学,2012,32(06)：81-85.

［4］李思达.总体最小二乘平差方法及若干测绘应用研究[D].中国矿业大学,2017.

［5］赵英文.总体最小二乘精度评定方法研究[D].东华理工大学,2017.