浅议初中数学圆的基本性质的复习

韩 朋

(贵州省遵义市播州区鸭溪中学，贵州 遵义，563108)

初中数学中的圆，是我们日常生活中早已熟悉的几何图形，学生在生活和学习中都已经有一定的了解，但是圆这一部分又常常是初中各种考试中的难点，经常都得分率不是很高，学生不容易掌握，本文结合具体例子，谈谈圆的基本性质的复习，供同行参考，与同行共勉。

1　圆的定义

平面内到定点的距离等于定长的点的集合叫做圆。

2　确定圆的条件

由下列条件之一，可确定一个圆。

（1）已知圆心和半径；

（2）已知直径的位置和长度；

（3）已知不在同一直线上的三点。

3　圆的基本性质

（1）同圆或等圆的半径相等，直径也相等。

（2）圆是轴对称图形，也是中心对称图形，都是它的对称轴，圆心是它的对称中心。

（3）在同圆中，直径是最大的弦。

（4）在同圆或等圆中，弧(指劣孤)、圆心角、弦、弦心距之闻有下列关系：

i)如果弧相等，那末所对的圆心角相等；所对的弦相等，并且弦心距也相等.如果两条孤不相等，那末大弧所对的圆心角较大，所对的弦较大，并且大弧所对的弦心距较小。

ii)如果弦相等.那末所对的圆心角相等， 弦心距相等，并且所对的弧相等.如果弦不等，那末大弦所对的圆心角较大，大弦的弦心距较小，并且大弦所对的弧较大。

（5）弦、弧和直径之间的关系(垂径定理)

i)垂直于弦的直径平分弦，并且平分这条弦所对的弧。

ii)过弦(不包括直径)的中点的直径垂直弦，并且平分这条弦所对的弧。

例题 1(弦 长的 计算) 已知；ΔABC中，∠C=90°，AC=6cm，BC＝8cm，以 C为圆心，CA长为半径画弧交斜边AB于D。求；月AD的长。

分析 AD是⊙C的弦，作斜边AB的高CE，利用垂径定理。

解：如图 1，作 CE⊥AB于 E，则 AE＝DE。

因为 AC=6cm,BC＝8cm

答：长为7.2cm。

例题 2(弦、孤、弦心距之间的关系) 如图 2，已知：P是⊙O内的一点，AB、CD是过P点的弦，∠APO=∠CPO。

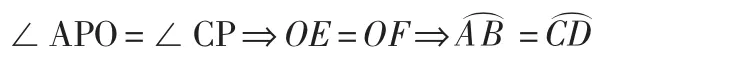
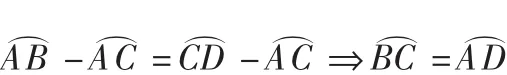
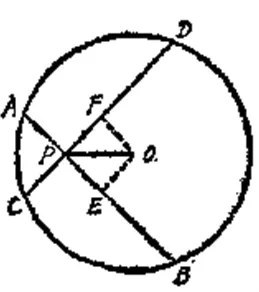
附注 在有关弦的问题中，常添弦心距作辅助线.这样既能直接应用圆的基本性质，又能组成直角三角形或矩形，便于与与直线形性质相联系.以上两例都表明了弦心距的这一作用，有时弦公距还是一个有关三角形的中位线。

作为一个重要的，不可忽视的内容，我们简单归纳性地提一下：

4　点、直线与圆的位置关系

4.1　点与圆的位置关系

（1）点在圆内⇔d＜r(r——圆的半径，d——直线到圆心的距离)

（2）点在圆上⇔d=r（3）点在圆外⇔d＞r

4.2　直线与圆的位置关系

（1）直线和圆相交⇔d＜r(有两个公共点)，(r——圆的半径，d——直线到圆心的距离)

（2）直线和圆相切⇔d=r(有一个公共点)，

（3）直线和圆相离⇔d＞r(无公共点)。

4.3　圆 的 切 线

（1）定义 和圆只有一个公共点的直线，叫做圆的切线，这个公共点叫做切点。

（2）性质

i)切线垂直于过切点的半径；

ii)过切点（或圆心）并和切线垂直的直线必定过圆心（或切点）。

iii)从圆外一点向圆引的两条切线的长相等，并且这点和圆心的连线平分两条切线的夹角。

（3）判定

i)经过半径外端并且垂直于这条半径的直线是圆的切线；

ii)如果圆心到直线的距离等于这个圆的半径，那未这条直线是圆的切线.

【参考文献】

［1］郑毓信.多元表征理论与概念教学[J].小学数学教育.2011(10),23-30.

［2］史宁中.《数学课程标准》的若干思考[J].数学通报.2007(05),41-45.

［3］吴曼.支架式教学模式原则浅谈[J].长春教育学院学报.2010(04),79-83.