超大型集装箱船载重量的设计方法研究
2018-03-31袁红良鄢慧敏
邓 恺,袁红良,鄢慧敏
(1. 上海交通大学 船舶海洋与建筑工程学院,上海 200030;2. 沪东中华造船(集团)有限公司,上海 200129)
0 引 言
进入 21世纪以来,随着贸易全球化的持续发展,全球贸易需求不断扩大,集装箱船进入了大型化的高速发展期。据统计[1],集装箱船总运力自1996年以来呈逐年递增的趋势,而集装箱船队总规模自2008年全球金融危机以来呈逐渐下降的趋势,这意味着金融危机之后超大型集装箱船在有限的新船订单中所占的比例呈井喷式增长。
回顾超大型集装箱船近10a来的发展历程可知,其发展并非简单的尺度扩张,在不同的发展时期有着不同的市场特征。本文大致将超大型集装箱船的发展历程划分为5个阶段,即起步期(2006—2007年)、阵痛期(2008—2010年)、转型期(2011—2012年)、高峰期(2013—2015年)和平缓期(2015年之后)。相较于传统集装箱船的设计,超大型集装箱船具有尺度大、载重量大、载箱量大、航速低和油耗低等新技术特点。服务航速、功率、载重量和重箱数等主参数指标相互交错、相互关联,如何在研发之初确定这些主参数,从而在新造船合同谈判中得到船东的青睐,是评判该设计方案是否成功的关键。若能通过分析已有典型超大型集装箱船的船型参数,从而得到超大型集装箱船载重量的设计及评价方法,不仅能为新船型初期的经济论证及研发设计提供有力依据,为新船型设计方案的产生提供可靠的方法和手段,还可为航运部门及船东选择最佳船型要素提供参考。
1 超大型集装箱船船型数据库及回归分析方法
本文选取40艘具有代表性的9000~21000TEU新一代超大型集装箱船建立船型分析数据库,该数据库能基本涵盖超大型集装箱船市场上的所有系列船型。各船型数据主要来自英国造船工程学会出版的《世界船舶精英集》(Significant Ships)中2009—2015年间的超大型集装箱船代表船型及部分公开船型资料。
本文以载重量指标为切入点,分别以船长L,船宽B,名义总箱数Nc,14t均箱数n等船型要素[2]为x坐标,以载重量为y坐标,绘制各要素与载重量之间的散点分布图,分析各要素与载重量之间的关联性,得到适用于超大型集装箱船载重量设计的回归经验公式。同时,以每箱每吨海里能耗指数J等指标为载重量指标合理性衡量因子,得到超大型集装箱船载重量设计指标评价方法。
本文采用回归分析法研究数据库中的船型要素组合与载重量的相关性,并将最常用的复相关系数 R2作为检验模型精确度的指标[3]。R2越接近于1,回归公式的拟合优度就越好。

式(1)中:y˜i为多项式在设计点i上的值;y˜为响应y的平均值。
2 超大型集装箱船载重量与船型要素的关系
2.1 超大型集装箱船载重量与长宽比L/B的关系分析
促使集装箱船大型化发展的外因是码头设施的升级及集装箱绑扎技术的进步,内因是供需环境改变带来的船型尺度的持续增大及载重量水平的持续提高。集装箱船为布置型船舶,其长和宽由集装箱布置的行数及列数决定。现以数据库中各船型结构吃水时的载重量为y坐标,以长宽比L/B为x坐标,分析超大型集装箱船载重量与主尺度之间的关联性。图1为载重量与长宽比L/B的关系散点图。
由图1可知,超大型集装箱船的载重量与长宽比L/B的关系并非简单的线性相关性,仅相同型号的船型就具有趋于一致的长宽比和载重量水平。具有最小长宽比的船型为船长300m,船宽48.2m的9000TEU级别集装箱船;具有最大长宽比的船型为船长 335m,船宽 42.8m的8500TEU级别集装箱船。值得注意的是,这两型集装箱船的载重量相当。
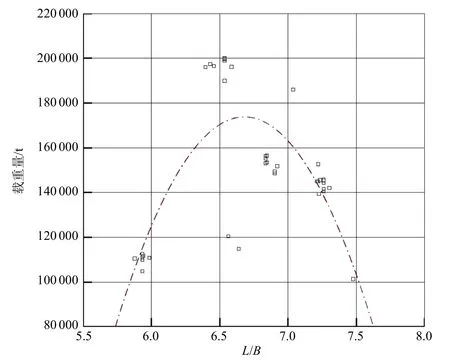
图1 载重量与长宽比L/B的关系散点图
DNV-GL最新发布的研究报告[4]表明:苏伊士运河的极限通航尺度限制(59m宽、17m深)是超大型集装箱船大型化发展最大的制约因素;对船长>400m的情况进行论证可知,增加现有船型的船宽及吃水是对设计改动影响最小的可提升名义箱数的有效途径;进一步增加船长虽然在理论上可一定程度地继续降低单箱成本,但面临着巨大的结构设计改变及无港可停的尴尬局面。
本文预测,未来超大型集装箱船不会轻易突破400m的船长界限,同时随着当前超大型集装箱船最大吃水已接近码头极限水平,市场上的新船型将会在9000TEU,10000TEU和14000TEU等现有船型的基础上增加1~2列,即L/B将分布在5.9~6.2区间,B/T分布在3.3~3.8区间,而载重量分布在16万~20万t区间。
2.2 超大型集装箱船载重量与名义总箱数的关系分析
集装箱船大型化发展的最直观表现是名义总箱数的持续增长,现以各船型的名义总箱数为 x坐标,以结构吃水时的载重量为y坐标,得到散点分布图及趋势线见图2。由图2可知,复相关系数R2为 0.9659,已非常接近于 1,表明超大型集装箱船载重量与名义总箱数之间存在较好的线性关联趋势。
根据图 2所示的趋势线,超大型集装箱船载重量DW与船型最大名义箱数Nc的关系可近似表示为
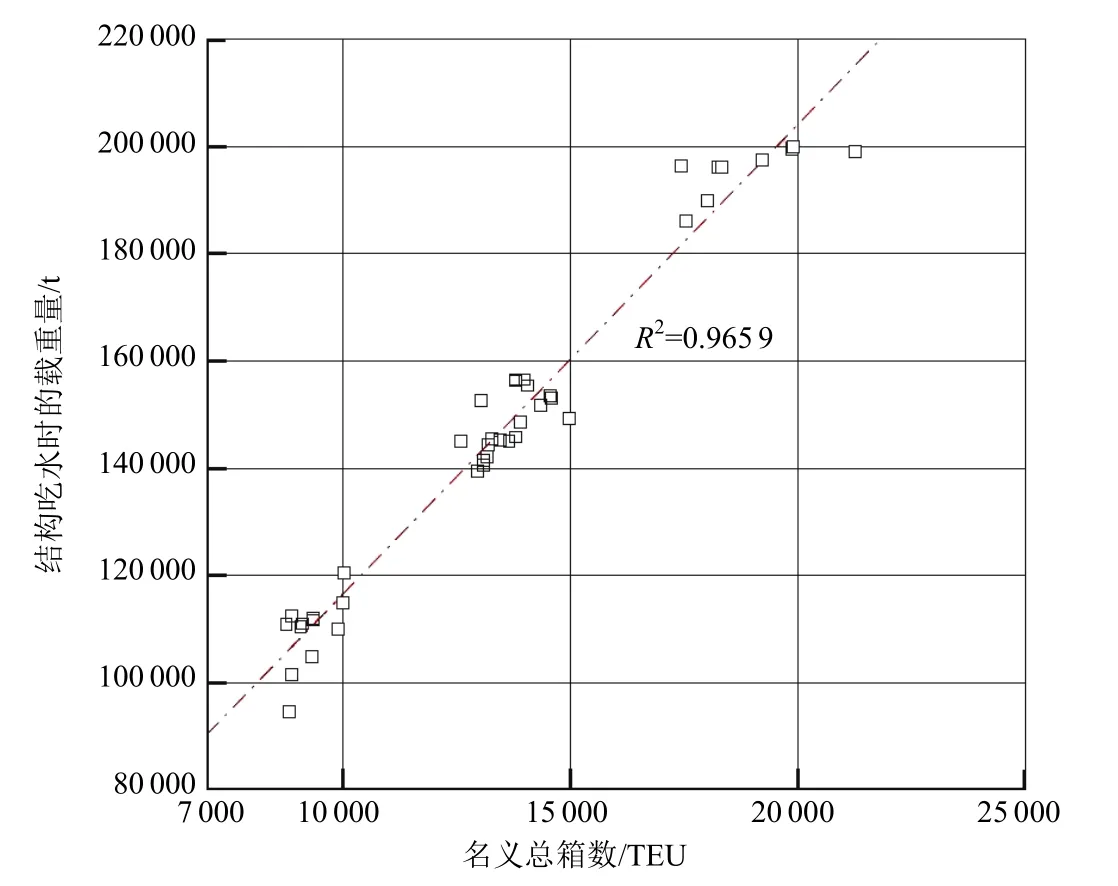
图2 载重量与名义总箱数关系散点图
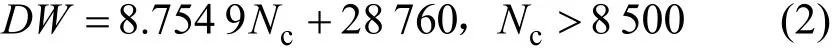
利用式(2),研发设计人员可根据目标船型的最大箱数指标快速估算出大致的载重量水平区间,实现新船型载重量指标的初步定位。
2.3 超大型集装箱船载重量与货舱内、甲板上箱数的关系分析
由于近年来绑扎技术持续进步及码头设施不断完善,绑扎桥由2层升级为3层,甲板上的堆箱高度由8层变为9层、10层或11层,使得近几年交付的新船的甲板上堆箱数激增,出现许多船型相同但总箱数不同的情况。这使得单一采用名义总箱数进行载重量预报的方法存在一定的片面性。结合本文采集的船型数据,下面3种9000TEU集装箱船具有相同的主尺度和载重量水平,但总箱数及甲板箱数以2012年交付的“ATHENS”最小、2015年交付的“ARKANSAS”最大。就船型设计而言,三者并无大的区别,仅仅是各自空气吃水及甲板上堆箱的层数不同。若直接套用式(2),则计算载重量分别为115398t,108561t和105540t,所对应的计算均值为109833t。表1为9000TEU代表船型要素对比。
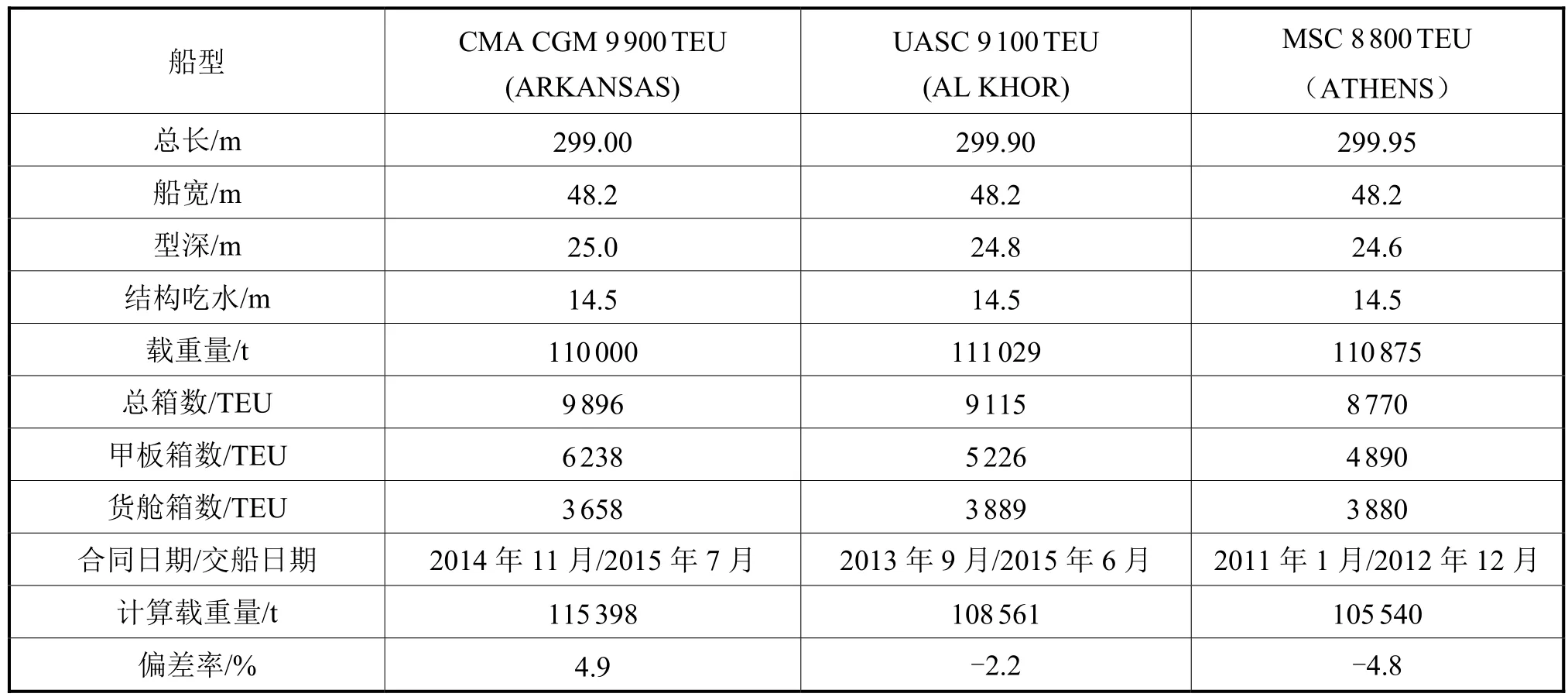
表1 9000TEU代表船型要素对比
单独采用名义总箱数进行目标船型的载重量估算无法体现新时期甲板箱数增多的最新技术趋势,可能会使预报值相对失真。对此,将从数据库中采集的名义总箱数Nc分为货舱内箱数Ni及甲板上箱数Nd,并
分别绘制Ni-载重量及Nd-载重量散点图(见图3和图4),分别得到回归公式


图3 载重量与货舱内箱数Ni关系曲线
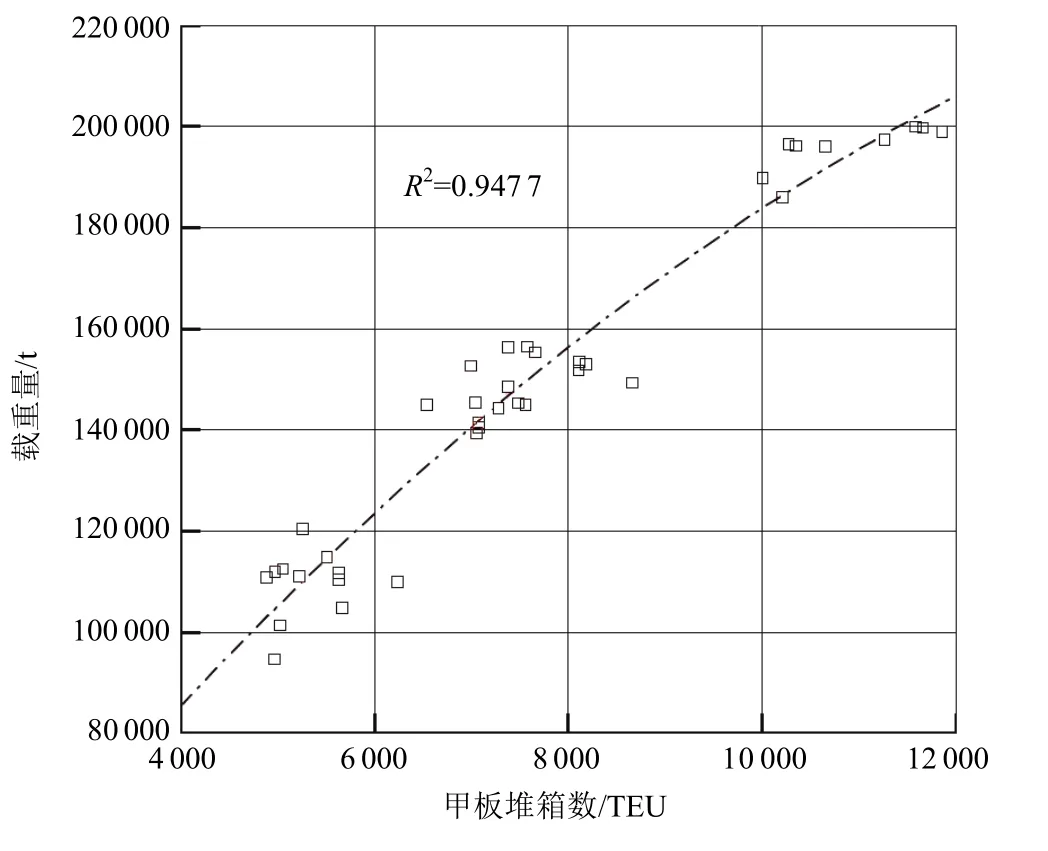
图4 载重量与甲板上箱数Nd关系曲线
式(3)及式(4)的复相关系数R2分别达到0.9629和0.9477,十分接近于1,是非常理想的。由图4可知,载重量与甲板的堆箱数Nd并不呈线性增长关系,曲率随着Nd的增加呈逐渐平缓的趋势,这与图3中曲线的走势形成鲜明的对比。由图3可知,随着货舱内箱数Ni的增加,载重量呈快速上涨的趋势,即上升曲率越来越大。从船型设计的角度看,货舱内堆箱数Ni属于每种船型独有的技术参数,其数值大小直接体现船舶结构吃水以下的线型胖瘦及排水量大小。由于Nd和Ni的数值需要在研发方案初步成型之后才能量化,故可在研发设计初期根据研发方案的目标总箱数Nc(式(2))进行载重量指标的预估算,在完成初步线型开发之后再根据货舱内箱数Ni(式(3))和甲板堆箱数Nd(式(4))对预估的载重量进行验证,并快速判断所研发船型的载重量是处于偏大风格还是偏小风格,以便在向船东及市场推介船型方案时具备快速响应的技术基础。
2.4 超大型集装箱船载重量与14t均箱数的关系分析
超大型集装箱船属于宽体类集装箱船,具有良好的稳性[5],在实际运营过程中所需压载水比较少,尤其是在承运的货物平均重量较大的工况下所需压载水几乎为零,重箱数的多少可代表载重量的大小。基于此,在集装箱船设计及商务决策领域,习惯将14t均箱数作为船型设计的重要衡量指标之一。现以各船型14t均箱数为x坐标,以结构吃水时的载重量为y坐标,得到对应的散点图及趋势线见图5。
根据图5所示的趋势线,超大型集装箱船载重量DW与船型14t均箱数n的关系可近似表示为

图5 结构吃水时的载重量与14t均堆箱数关系曲线
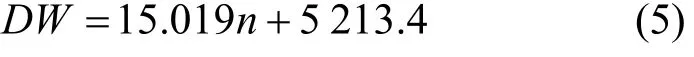
图5所示的趋势线印证了14t均箱数越大船型载重量越大的技术特点,且复相关系数R2为0.9190,表明式(5)的线性回归效果良好。在应用中,若在招投标时已知船东对14t均箱数的要求,则可通过式(5)直接估算目标船型的载重量水平,并与船东的目标载重量相对比,以此快速判断出船东的船型技术要求是属于偏载货量型还是偏快速性省油型,以便在较短的时间内调整设计思路,使新船型设计方案满足船东需求。
3 超大型集装箱船载重量经济性评价方法
船型设计是系统工程,设计方案的优劣并不仅仅取决于载重量的大小,更不能简单地认为载重量越大越好,或载重量的选取越接近利用经验公式计算得到的数值越好。
DNV-GL在其最新的研报[6]中强调,对超大型集装箱船进行优化应着力于有效降低船型单位货品的实际油耗成本,并与载重量、稳性、线型及轻重箱等指标息息相关。
业界曾将每箱每海里能耗指数[7]的大小作为船型经济性能的评估依据,由于本文主要研究载重量与船型参数的关系,故在其基础上引入载重量指标,重新定义每箱每吨海里能耗指数J,并将其计算式表示为

式(6)中:sP为主机最大装机功率 SMCR;Nc为最大名义箱数;Vs为设计吃水下的服务航速;DWs为结构吃水时的载重量。
能耗指数J作为船型经济性评价工具之一,用来指导未来新的船型设计方案,需保证其先进性。因此,所参照的船型不应继续按照数据库中的全部船型取加权平均的方式选取,而应当剔除旧船型,筛选出 2012年以后交付的符合时代潮流的较先进的船型进行数据分析。按照此原则,以结构吃水时的载重量DWs为x坐标,以能耗指数J为y坐标,绘制关系散点图(见图6),得到能耗指数J的幂函数回归公式(见式(7))为

图6 每箱每吨海里能耗指数J与结构吃水时的载重量关系散点图

采用幂函数得到的能耗指数J回归公式,复相关系数R2达到0.9548,且圆弧型的趋势更贴近于超大型集装箱船的船型发展特点。从图6中可看出,能耗指数J随着载重量的增大而持续降低,且近几年最新交付船舶的能耗指数J基本分布在趋势线下方。船型越小,代表单位成本竞争力的能耗指数 J上涨越明显;随着船型尺度的持续增大,能耗指数J显著下降;当大型化发展到船型极限临界区间以后,能耗指数J降速趋于平缓。能耗指数J的走势不仅证明了集装箱船大型化确实能实现单箱成本的有效降低,也体现着超大型集装箱船研发设计水平的持续进步,未来超大型集装箱船市场势必会呈现新老船型加速更替的趋势。
由于Vs实际上是船型在设计吃水时载重量DW对应的主机持续输出功率PNCR下的服务航速,且货舱内堆箱数 Ni与船型线型设计的关系比名义箱数Nc更加密切,可引入修正因子J1,用以分析船型设计吃水时的载重量DW所对应的每箱每海里能耗水平,其计算式为

图7为修正能耗指数J1与设计吃水载重量DW关系数点图。由图7可得到超大型集装箱船船型设计吃水时载重量对应的修正能耗指数J1的幂函数回归公式为

由于以往习惯于将结构吃水下的最大载重量DWs作为合同考核指标,故数据库中许多船型在设计吃水下的载重量DW信息较难收集,导致式(9)的复相关系数R2为0.9226,回归效果略低于式(7)。因此,在应用上述载重量经济性评价公式时,应以评价指数J为主,将指数J1作为船型经济性判断的双重验证和补充。
4 结 语
本文通过对超大型集装箱船典型船型的数据进行整理分析,分别基于目标船型最大名义箱数Nc,货舱内箱数Ni,甲板上堆箱数Nd和14t均箱数n得到适用于超大型集装箱船载重量指标估算的4个经验回归公式。同时,引入载重量的每箱每吨海里能耗指数J和修正因子J1,作为超大型集装箱船的经济性指标的评价因子之一。基于载重量的超大型集装箱船设计评价流程图见图8,为超大型集装箱船的研发设计提供参考。
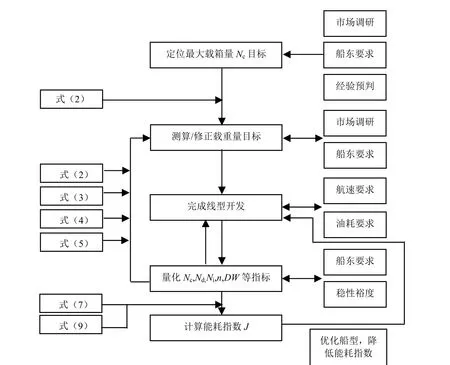
图8 基于载重量的超大型集装箱船设计评价流程图
【 参 考 文 献 】
[1] ALPHALINER. Alphaliner weekly newsletter[J]. 2016 (11), 31.
[2] 王运龙,金朝光,林焰,等. 集装箱船船型要素数学建模研究[J]. 武汉理工大学学报,2011, 35 (5): 914-917.
[3] 张恒,詹成胜,高祖源,等. 基于船舶阻力性能的船型主尺度参数敏感度分析[J]. 船舶工程,2015,37 (6): 11-14.
[4] PROBST J O. Pump up the volume[J]. DNV-GL Container Ship Update, 2016 (2): 4-7.
[5] 余建伟,尹逊滨. 9200TEU集装箱船稳性研究[J]. 船舶标准化工程师,2013 (4): 41-44.
[6] HOLLENBACH U. Optimizing concept designs[J]. DNV-GL Container Ship Update, 2016 (4): 9-11.
[7] 刘英良. 基于CFD的超大型集装箱船线型优化设计[D]. 广州:中国船舶与海洋工程设计研究院,2014.
