粘土矿物力学特性研究

2018-03-30黄大勇

科技视界 2018年31期

黄大勇

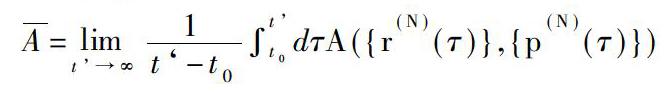
【摘要】粘性土的宏觀力学特性在很大程度上取决于所含粘土矿物的微观表现，构建了高岭石的多晶模型，采用分子模拟的方法研究高岭石的力学特性。模拟时，首先消除不合理的局域原子排布，然后对弛豫后的晶体沿Z轴和X轴分别均匀施加应变，再弛豫使系统平衡，重复此拉伸过程、弛豫过程，直至晶体断裂。依据所得到的数据，可以绘出黏土矿物的应力-应变曲线，进而可得相关材料的弹性模量E和泊松比μ，结合粘性土中所含黏土矿物的种类、比例、分布情况，可用于判断粘性土地基的工程性质，对于工程实践具有重要参考价值。

【关键词】粘性土地基；黏土矿物；微观结构；力学性能

中图分类号： P574；P315 文献标识码： A 文章编号： 2095-2457（2018）31-0256-002

DOI：10.19694/j.cnki.issn2095-2457.2018.31.123

0 引言

通常，粘性土的工程性质由其宏观力学参数描述，但本质上，这些性质却取决于其矿物成分的微观力学表现。因此，黏土矿物的微观力学特性研究就变得非常重要。

目前，一些科研人员已经开始尝试从微观层面来研究工程材料的力学特性，如郭雅芳等研究了体心立方铁的微观裂尖发展机理，谭云亮等研究了非匀质材料的细观破坏机理，李育枢等研究了岩爆岩石的微观破坏力学机制等。然而，从微观层面进行黏土矿物的力学性质研究的工作还较少。

1 分子模拟过程

对分子系统的模拟可以分为四个步骤：首先是设定模拟所采用的势函数及系综；第二，给定初始条件；第三，系统平衡计算；最后，计算宏观物理量。

1.1 势函数的选取

对于分子模拟而言，最重要的两个要素是初始结构的给定和原子间作用势的确定。而影响结果精确程度的最主要的因素是原子间作用势的精确性。

当前，用于分子模拟的势函数可划分为经验势和非经验势两类，虽然势函数发展的方向是非经验势，但现在非经验势的研究还很不成熟，得到的结果差别也很大，因此，采用经验势中的BMH双体势函数进行计算。

1.2 系综的选取

分子模拟，必须要在一定的系综下进行，本文采用正则系综（NVT）。在此系综中，系统的原子数（N）、体积（V）和温度（T）都保持不变，并且总动量为零。正则系综的量子表达式为：

1.3 初始条件的确定

合理的初始位形和初始速度有利于系统快速的弛豫到平衡状态。令初始位置在差分划分网格的格子上，初始速度从Maxwell-Boltzmann分布随机抽样而得到。

1.4 系统平衡计算

模拟时，首先对晶体模型进行弛豫，弛豫时间步长设定值为0.005ps。采用Berdensen方法进行等温调节，利用Predictor-Corrector算法，使系统能量最小化，同时采用Parrinello-Rahman自由收缩，以保持系统应力为零，从而消除不合理的局域原子排布，使系统达到平衡。

1.5 计算宏观物理量

宏观物理量是沿着相空间轨迹求平均来计算的。对于一个宏观物理量A，它的测量值应为平均值A（-）。如果已知初始位置和动量为{r（n）（0）}和{p（n）（0）}（上标表示系综N个粒子的对应坐标和动量参数），选择适当的算法求解具有初值问题的运动方程，便可得到相空间轨迹{r（n）（t）}，{p（n）（t）}。对轨迹平均的宏观物理量A的表示为：

2 高岭石的分子动力学研究

2.1 高岭石分子模型的建立

高岭石（[Al4（Si4O10）（OH）8]）是由硅氧四面体片与铝氧八面体片按1：1方式连结形成的结构层，沿c轴堆垛而成，层间没有阳离子或水分子存在，强氢键（O-OH=2.89？魡）加强了结构层之间的连结。

高岭石的晶胞模型建立参数如下：

（1）建立单位晶胞模型空间群：群号是P1，三斜晶系。

（2）输入所建模型的基本晶胞参数，建立晶胞单元：a=5.148994？魡，b=8.933998？魡，c=7.384？魡，α=91.930°，β=105.04196°，γ=89.791°。

（3）在晶胞单元中输入各种类型原子的空间坐标，形成的单晶胞模型如图1。

（4）建立超晶胞。CASTEP计算是在周期性重复的单晶胞上执行的，因此，建立4×4×4的超晶胞模型，如图2。

2.2 高岭石晶体模型的结构优化

（1）交换-关联函数：选择GGA下的PBE形式的关联函数。

（2）赝势：选择Ultrasoft赝势。

（3）截断能：由于在CASTEP中，分子轨道是通过平面波基来扩展，而平面波基的数目是通过截断能的高低来控制，因此，宜在保证计算精度的前提下选择尽可能低的截断能。通过选取几个截断能进行试算，这里选择350eV。

（4）布里渊区抽样设置：布里渊区的设置是通过K点的设置来反映的，这里按精度设置，选择‘Fine。

（5）结构优化收敛精度：共设定四个优化参数，即能量的收敛精度为5.0e-4eV/atom；每个原子的最大力收敛精度为0.02eV/A；最大应变收敛精度为0.05GPa；最大位移收敛精度为0.001？魡。这些收敛精度指的是两次迭代求解之差，只有当某次计算的值与上一次计算的值相比，小于设置的精度时，计算才停止。

可以看到，晶胞已达到设定的结构优化收敛精度。经结构优化后的高岭石晶胞如图3，图4所示。

2.3 高岭石晶体的弹性常数计算

在上述经结构优化的高岭石晶胞的基础上，计算高岭石的弹性常数，计算结果如表1、表2所示。

3 结语

通过分析黏土矿物高岭石的力学性质，我们可以得到以下结论：

（1）计算得到的黏土矿物力学性质较宏观测量值为大，原因应该是晶胞建模时，没有考虑材料实际结构中的各种缺陷，结构较为"纯净"造成的。

（2）从高岭石这种黏土矿物的晶胞模型可以看出，其为层状结构，且泊松比在X、Y、Z三个方向并不相同，这从微观层面证明了土的各向异性力学特征产生的原因。

（3）随着分子含水量的增加，材料弹性模量却迅速减小，宏观上就表现为黏土的硬度随着含水量的增加而减少。

【参考文献】

[1]郭雅芳，高索文.分子动力学模拟裂纹扩展及相关尺寸行为[J].北京交通大学学报，2005，29（4）：5-9.

[2]谭云亮，周辉等.模拟细观非均质材料破坏演化的物理元胞自动机理论[J].物理学报，2001，50（4）：704-709.

[3]李育枢，郑建国，李天斌.电站隧洞岩爆岩石的微观破坏力学机制分析[J].水利发电，2006，32（8）：17-20.