考虑封严容腔的涡轮非轴对称端壁优化目标研究

潘贤德 吕剑波

（中国航发商用航空发动机有限责任公司，上海 200241）

叶轮机械中的损失大致可分为叶型损失、端区二次流损失和叶尖泄漏损失三类[1]。其中，端区损失主要产生于二次流以及端区边界层内的黏性摩擦作用，在小展弦比涡轮叶栅通道内，端区损失占总损失的比例可达30%～50%，在升力系数较大的大展弦比涡轮叶栅中，二次流问题变得更加突出。非轴对称端壁造型作为一种先进的二次流控制技术，其基本原理是基于二次流的产生和发展机理，通过端壁形状的改变来减小端壁处从压力面到相邻叶片吸力面的压力梯度，减缓通道涡下部的新边界层生成，抑制二次流的发展，以此来削弱涡轮通道内的二次流损失。

Rose最早提出了非轴对称端壁的概念，相关研究表明，这种方法是减小端区二次流损失的有效途径之一。非轴对称端壁设计技术已在国外多个民用航空发动机上得到应用，如罗罗的遄达系列发动机、GENX及LEAPX等。在国内，中国航发商用航空发动机有限责任公司在非轴对称端壁技术研究方面开展了大量的工作。唐慧敏等率先基于非均匀有理B样条曲面造型和网格变形技术搭建了非轴对称端壁优化设计平台，并采用PW公司公开发表的PackB涡轮平面叶栅数据对所开发的工具进行验证。结果表明，采用搭建的平台优化出的非轴对称端壁与文献中经过试验验证的几何特征基本一致。随后，其采用该设计工具在Lisa 1.5级轴流涡轮上进行了非轴对称端壁设计，提炼的优化方法使得涡轮级效率提高了0.4个百分点。为进一步验证非轴对称端壁设计效果，对Lisa涡轮上的非轴对称端壁设计方案开展了非定常计算。结果表明，在非定常条件下，带非轴对称端壁设计的涡轮效率增大0.3个百分点，对流场细节的分析也进一步验证了非轴对称端壁的设计效果。在此基础上，胡书珍等在某高压涡轮导叶端壁开展了非轴对称端壁优化设计，并且设计了扇形叶栅试验对设计效果进行验证。设计结果中端壁优化使得导叶总压损失系数减小3.44%，试验结果中总压损失减小达5.67%，流场测量结果也显示非轴对称端壁设计对于提升叶栅效率、减小通道内二次流损失效果明显。

非轴对称端壁设计是减小端区二次流损失的有效手段，但是其设计特征与叶栅内部流动密切相关，为寻求更好的设计结果往往需要进行大量的CFD计算，国内外普遍采用计算机自动寻优的方法进行优化设计，其中合理的优化目标是自动寻优的关键，不同的目标函数获得的设计结果也不尽相同。本文采用自主搭建的非轴对称端壁优化设计平台在某高升力低压涡轮叶栅下端壁进行非轴对称端壁造型，分别选取总压损失、SKEH及二者的组合参数作为优化目标对不同的目标函数进行研究，通过详细对比流场细节对三种目标函数进行评价并分析了非轴对称端壁设计中应关注的因素。

1 非轴对称端壁优化设计平台

非轴对称端壁优化设计平台基于Matlab、Isight和CFX进行搭建，集几何造型、网格自动调整、CFD数值模拟和自动寻优于一体，如图1所示。其中，Matlab用于非轴对称端壁造型的网格读取与自动造型，CFX为三维数值模拟工具，Isight提供优化平台和算法，网格生成分为端壁几何生成和网格变形两步，由自主开发的NURBS曲面造型工具和网格变形程序实现。

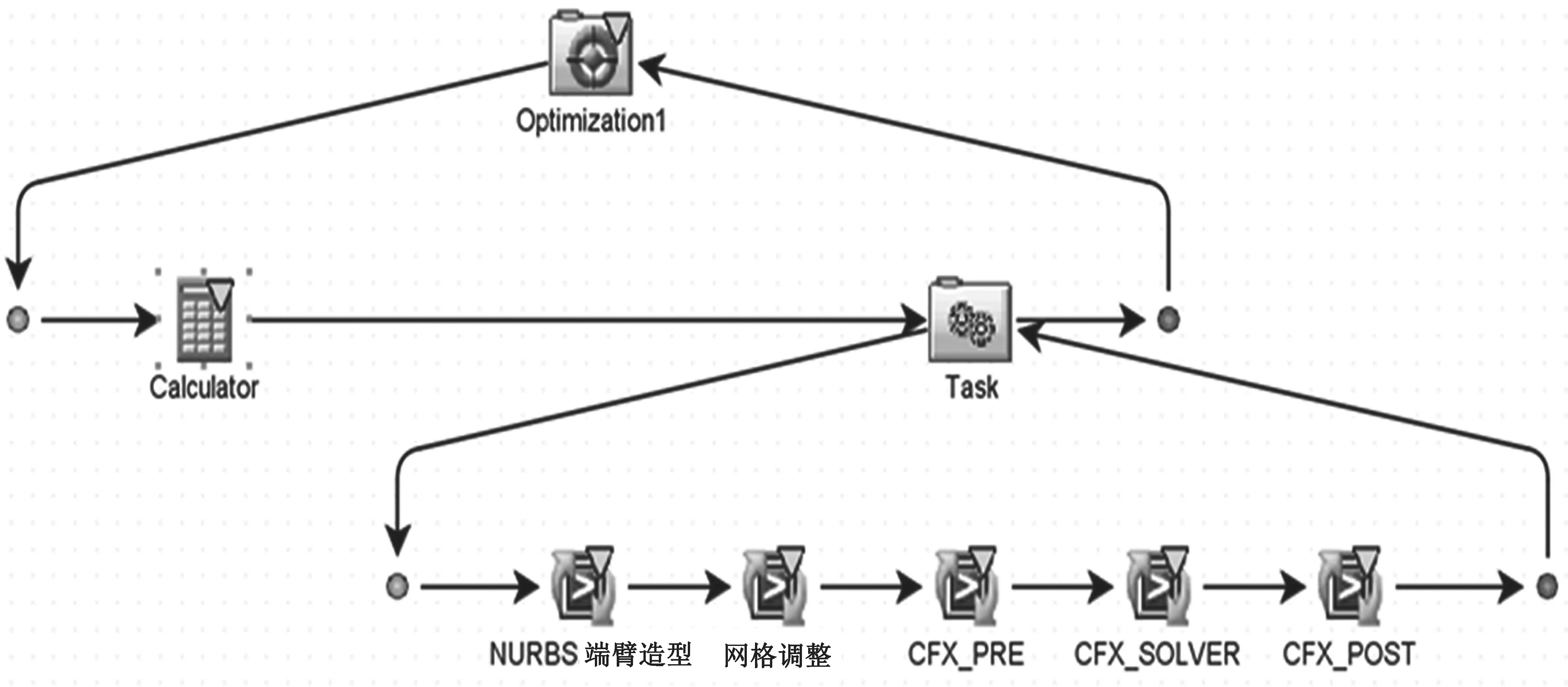
图1 优化设计平台

2 优化目标函数

非轴对称端壁造型的目标是在保持主流出口流量和出口气流角基本不变的前提下削弱端区二次流，最小化端区损失，选择一个合适的优化目标函数对设计效果尤为重要。

在涡轮气动设计及叶栅试验中，叶片排的总压损失系数常被用来量化叶排的损失大小，在工程设计中有重要价值，人们在研究中会以总压损失作为端壁优化设计的目标函数。无量纲的总压损失系数存在多种定义，本文采用以式（1）定义的总压损失系数作为第一种目标函数。

式中，Pt0为入口总压；Pt1为出口总压；Ps1为出口静压。

由于现有的CFD方法难以准确预测总压损失，而二次动能主要受无粘效应的影响，可被CFD更准确地预测，本文选择二次动能SKE与流向旋度Helicity的点积SKEH作为第二个优化目标函数。SKEH是与二次损失直接相关的物理量，可用于评估二次流损失的大小。SKEH的定义为：

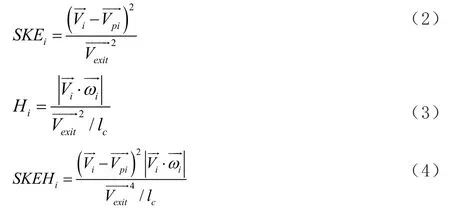
式中，Vexit为出口质量平均速度矢量；Vpi为节点i的速度矢量Vi与周向质量平均速度Vm组成的合成项；ωi为当地的涡量矢量；lc为特征长度，通常取叶片弦长。

质量平均的SKEH定义如下：

在开展非轴对称端壁设计时，单独关注总压损失或者单独关注二次动能有可能得到二者变化趋势相反的情况，此情况可能表明所设计的非轴对称端壁获得收益的风险较大。考虑到这一问题，本文在优化设计时还选用了第三个优化目标函数φ，其定义为总压损失和SKEH的组合参数，如式（7）所示。

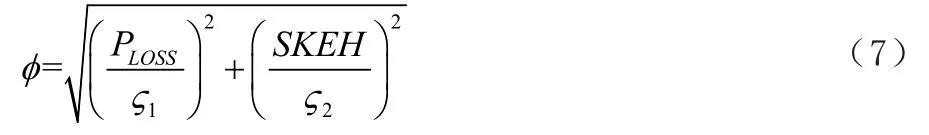
式中，ζ1为轴对称端壁条件下的总压损失；ζ2为轴对称端壁条件下的SKEH值。

如此处理可使组合参数φ中总压损失和SKEH两项的量级相当，从而可以综合考虑总压损失和SKEH，一定程度上降低非轴对称端壁设计的风险。

3 计算模型及方法

3.1 研究对象

本文工作基于某高升力低压涡轮环形叶栅开展，全环叶片数为262片，叶片高度150.00 mm，轴向弦长75 mm，展弦比2.0，叶栅栅距91.58 mm，稠度为0.819，安装角（与轴线夹角）为34.6°，叶型载荷系数达到1.57，压力分布为后加载特征。二维叶型如图2所示，取其下端区作为非轴对称端壁造型区域。

3.2 计算域及网格划分

在涡轮真实工作环境中，由于轮缘封严气对端区二次流的生成和发展有较强的影响，如图3所示，封严容腔的存在显著改变了端区叶栅前缘的流动特征，尤其是鞍点位置[3-4]。考虑到叶栅前缘附近是非轴对称端壁造型的一个重要区域，本文在计算时考虑了容腔效应，容腔经过简化，保留了主要的结构特征。

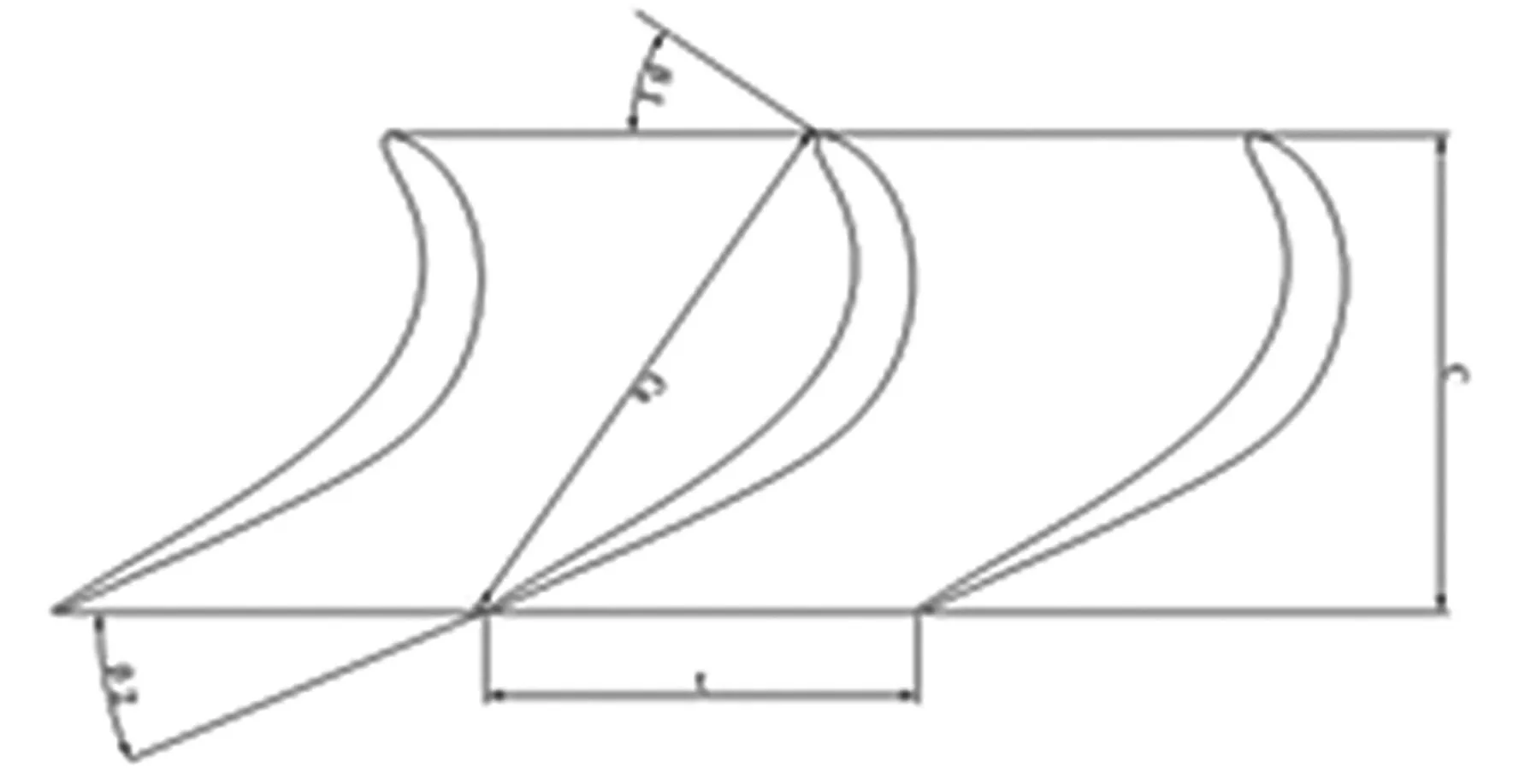
图2 二维叶型

计算域如图4所示。入口域轴向长度为5倍叶片轴向弦长，为叶片排入口提供入口边界层条件，采用单通道计算。计算网格采用ANSYS TurboGrid生成以便于采用脚本文件进行控制，单通道网格数为99W，径向网格数71层，O型网格和端壁网格y+控制在1.0左右。

图3 容腔对端壁表面流线的影响

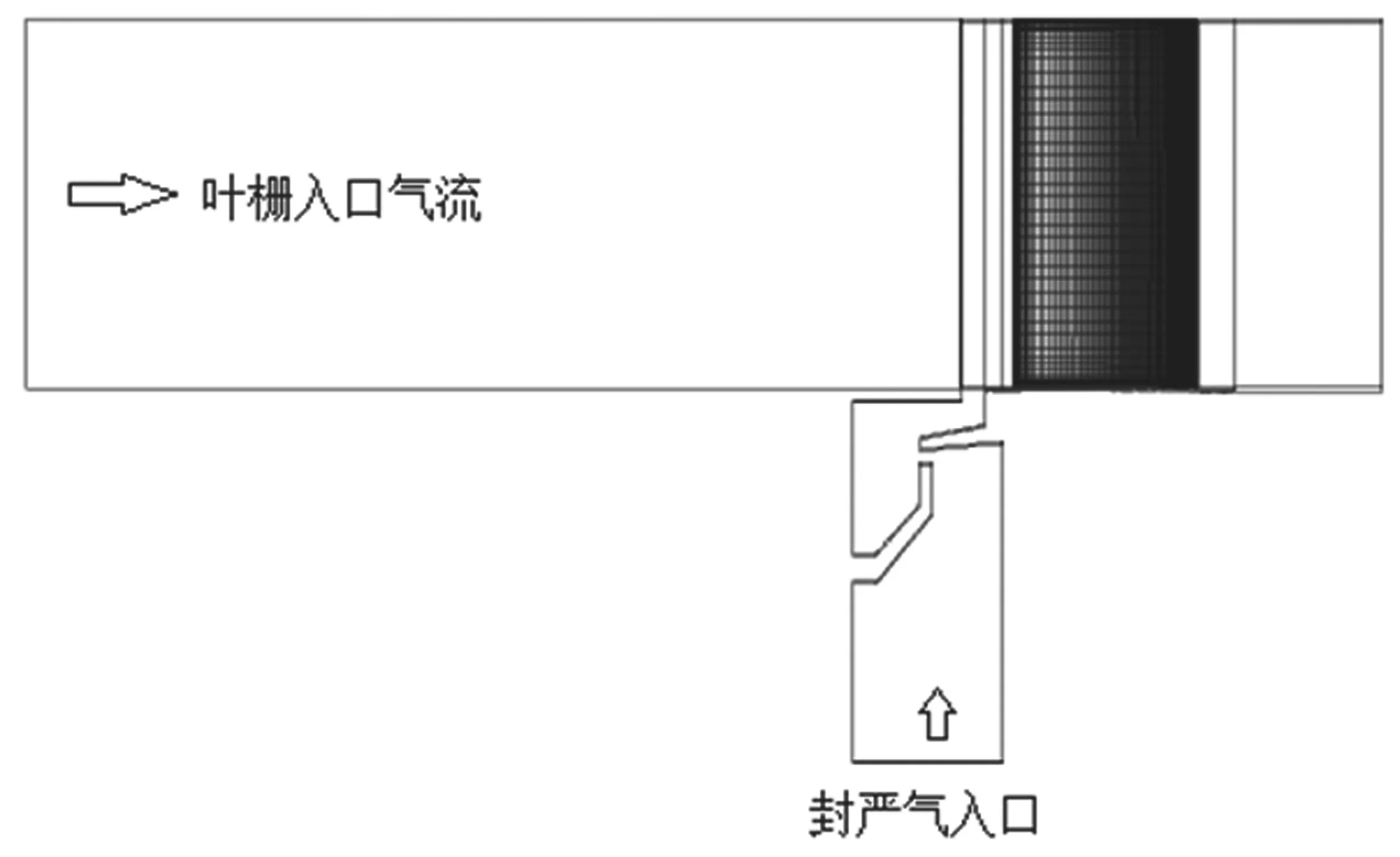
图4 计算域设置

3.3 计算设置

叶栅进口给定平均总温、速度和方向，出口给定平均静压；壁面绝热无滑移；周向两侧给定旋转周期性边界，边界上对应点参数相等；计算时轮缘封严容腔入口给定流量、总温，方向为垂直边界进气。湍流模型采用SST湍流模型，入口湍流度设置为1%。

4 结果及分析

表1给出了不同优化目标函数的优化结果，其中BASE为轴对称端壁设计，即优化基准。由表1可知，在保持叶型升力系数、流量及出口气流角基本一致的前提下，总压损失目标函数得到的结果，总压损失下降最多，比BASE方案降低7.85%，同时SKEH下降了28.3%；以SKEH为目标函数的优化结果，SKEH数值下降最多，但总压损失反而增大。综合考虑总压损失和SKEH两个因素，以φ为目标函数的优化结果，SKEH下降幅度与以SKEH为目标函数的结果相近，总压损失与以总压损失为目标函数的结果接近，但降幅都略有减小。

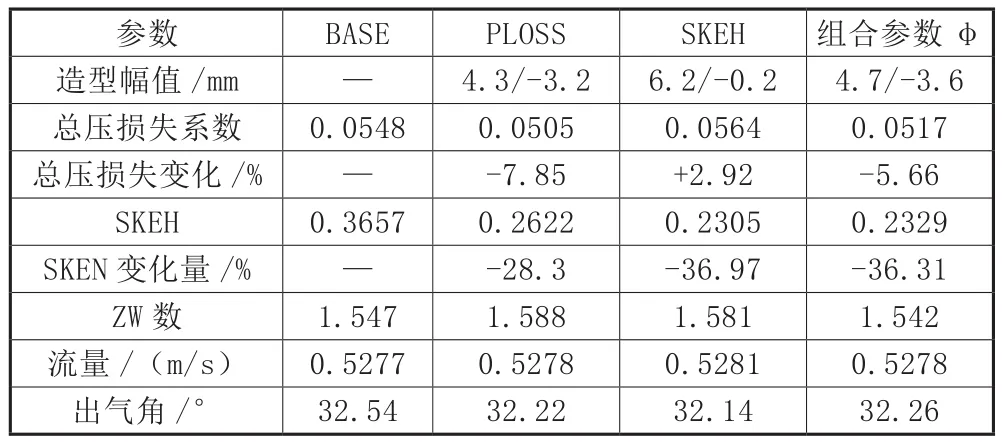
表1 各优化算例计算结果

图5为三种优化目标得到的端壁形状径向高度云图，单位为毫米，半径为正表示上凸，为负表示下凹。对比发现，使损失降低的端壁造型方案（PLOSS和φ），通道前半部分吸力面侧均为下凹特征，压力面侧则为上凸造型，但是位置有所差异，而损失略高的方案（SKEH）吸力面无下凹特征，这一特征可能对损失降低有较大的益处。

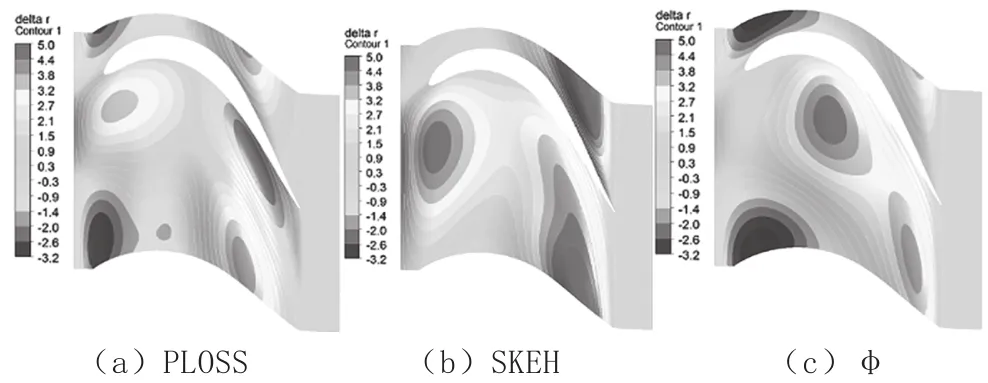
图5 三种优化目标得到的端壁形状径向高度云图

4.1 涡量分布

图6 给出了四个结果叶栅通道内同一水平下的涡量分布，由图可见，封严出流对端区二次流的发展有重要影响。在PLOSS和φ结果中，端壁造型改变了封严气的出流方向和形式，往压力面方向产生一个的漩涡，该漩涡的产生与前缘压力侧上凸吸力面下凹的造型特征有关，其对马蹄涡的压力面分支有显著的抑制作用。在封严出流的作用下，马蹄涡的压力面分支强度被削弱且方向发生改变，被推离相邻叶片的吸力面，可以延迟通道涡的发展。

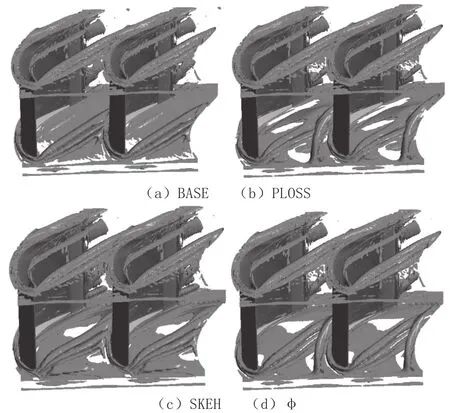
图6 通道内同一水平下涡量分布

而在SKEH结果中，进口处未发现漩涡特征，推测由于SKEH优化过分专注于削弱通道内的二次动能，连同进口的封严气出流特征也被其遏制，因此总损失降低不明显。另外，PLOSS结果中在轴向通道中后部端区产生再生涡量，SKEH结果中此再生涡量更加明显，这部分二次流对通道涡的发展起到了助推作用，而在φ结果中通道中后部未见此特征，表明φ结果中通道中后部的二次流得到有效控制。

4.2 壁面流线对比

图7为叶栅下端壁表面静压分布云图和表面流线图。根据图中端壁表面流线，人们可以看出PLOSS和φ结果。一方面，端壁的存在导致轮缘封严气进入主流的路径和形式发生变化，其在叶栅进口处与马蹄涡压力面分支的交汇点在端区造型的作用下被推离叶型的吸力面，通道涡到达相邻叶片吸力面的位置在轴向方向明显更加靠后，延迟了通道涡的发展。另一方面，从压力面到吸力面的横向压差减小，使得为马蹄涡压力面分支提供补给的端区横向流动削弱，有利于降低二次流损失。在SKEH优化结果中，端区流线方向相对于基准方案未发生较大改变，马蹄涡压力面分支与叶型吸力面的交汇点也未明显向后移动。

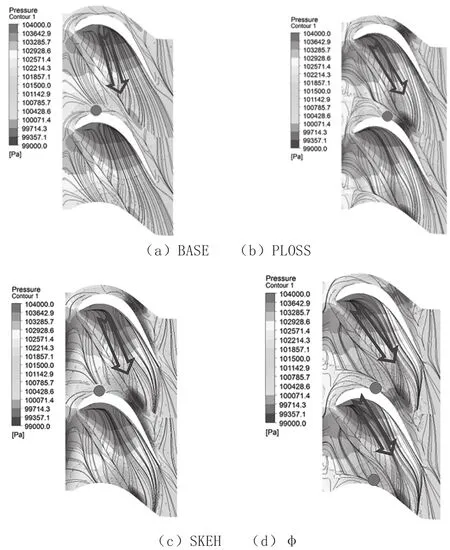
图7 端壁静压和表面流线图

图8 给出了四个方案叶身表面流线的分布情况，可以看出在PLOSS和φ的优化结果中，叶身主流区域径向范围明显变大，下端区二次流区域明显减小，二次流损失得到有效控制，而在SKEH结果中主流范围与BASE方案相当。

4.3 载荷分布的对比

图9给出了含BASE方案在内的四个方案1%叶高截面处的表面静压分布，可以看到，三个优化方案中叶型前部和中部的横向压差均减小，有利于减弱近前缘端区的二次流动。其中，组合参数φ的优化结果前部横向压差降低幅度最大，PLOSS结果降幅次之，SKEH结果降低幅度最小。叶栅后部的载荷均有不同程度的增大，组合参数φ增加幅度最小，PLOSS结果次之，SKEH结果增加幅度最大，叶型的负载整体向后移动。

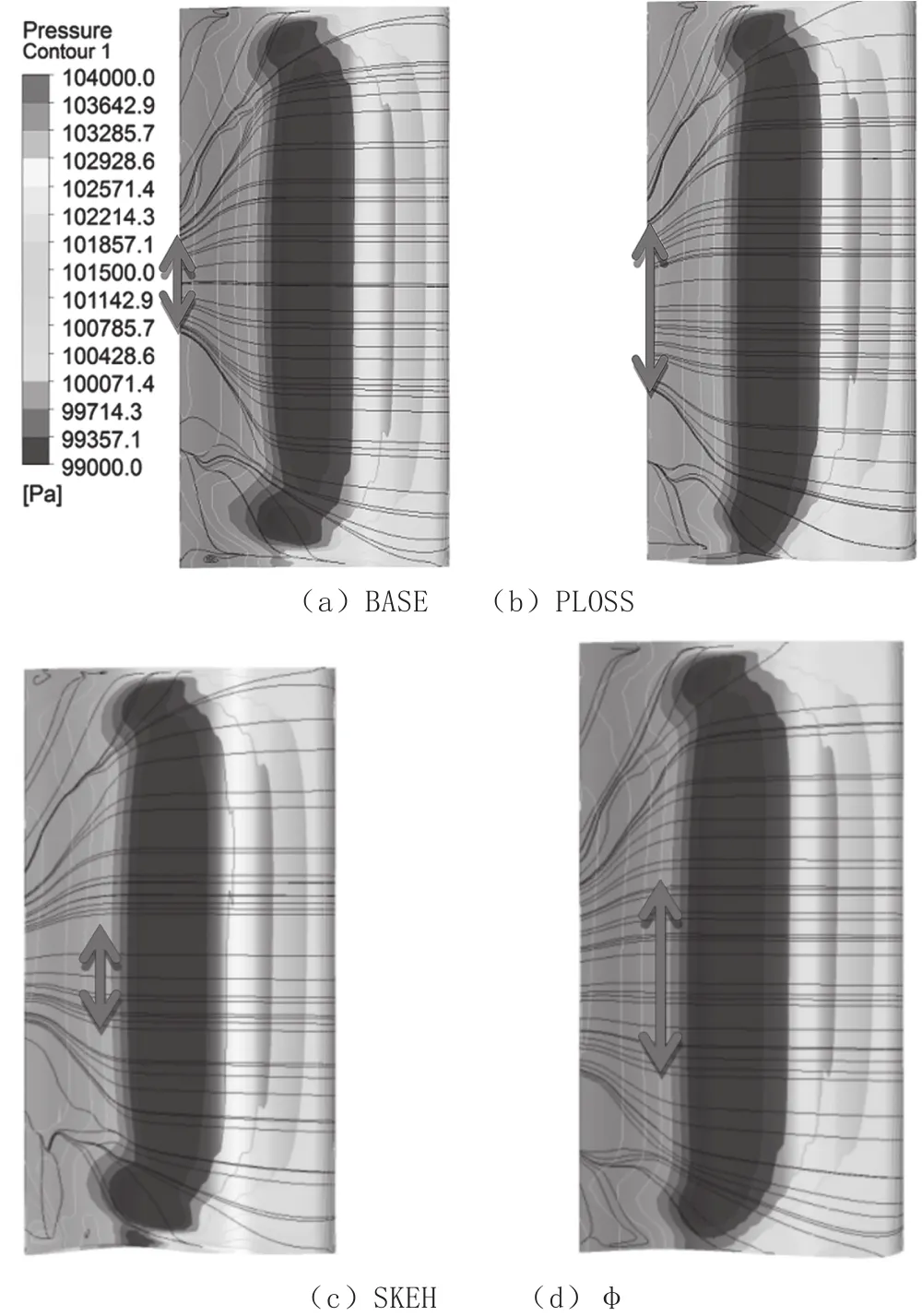
图8 叶身表面流线图

由于横向压差的减小，马蹄涡的压力面分支到达相邻叶片吸力面的时间被推迟，通道涡失去了充分发展的机会，这与前面所述的端区表面流线显示的结果相吻合。另外，负载后移将导致峰值马赫数变大，有可能会带来较大的损失，因此从对比来看，组合参数φ的优化效果最好，SKEH的优化效果最差。

4.4 总压损失分布对比

总压损失除了作为优化目标外，还可用作涡轮工程设计分析中常用的评价设计结果的分析参数。图10为四个方案的叶栅出口截面总压损失云图，由图可见：PLOSS和φ的优化结果中下端区总压损失均有所减小，且通道涡高度更贴近下端壁面，在周向方向上通道的范围也得到一定的控制，下端区通道涡得到削弱；SKEH的优化结果显示，下端区总压损失增大，对通道涡高度影响较小，从损失云图可知，下端区通道涡明显变强；优化方案的上端区总压损失未发生大的变化。

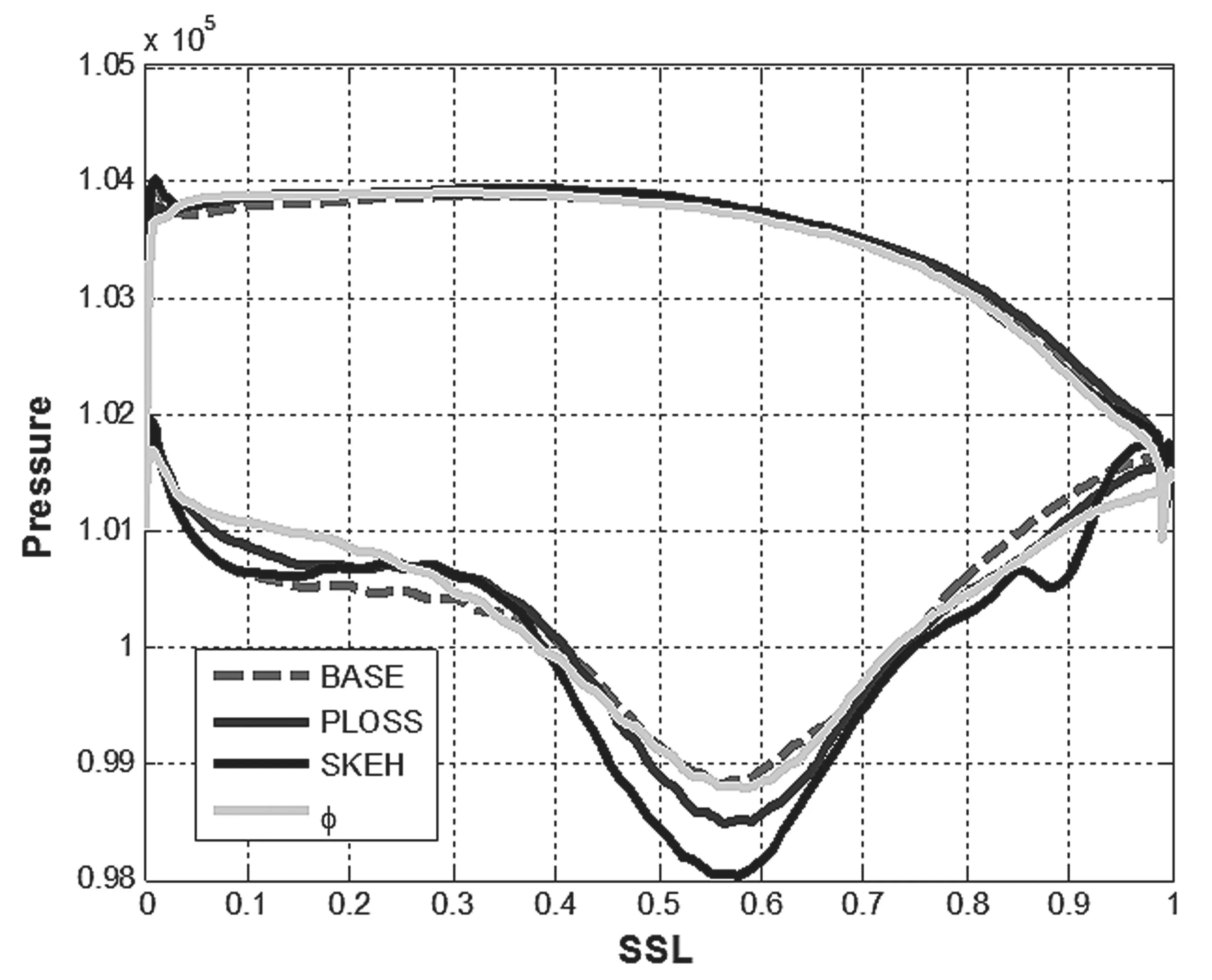
图9 叶根附近表面压力分布

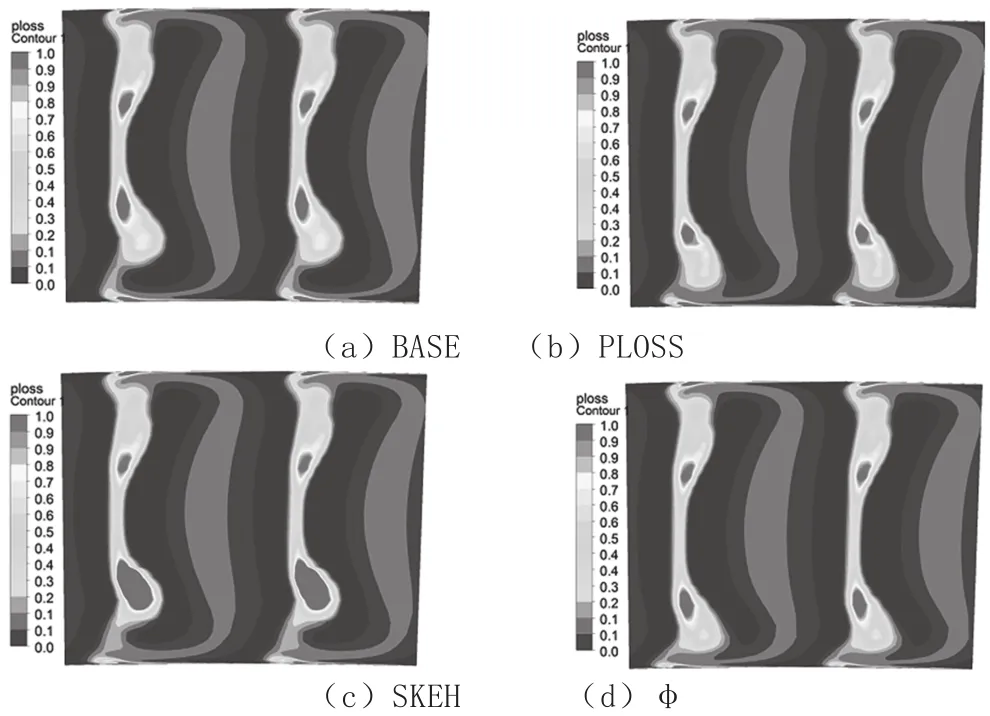
图10 出口总压损失云图

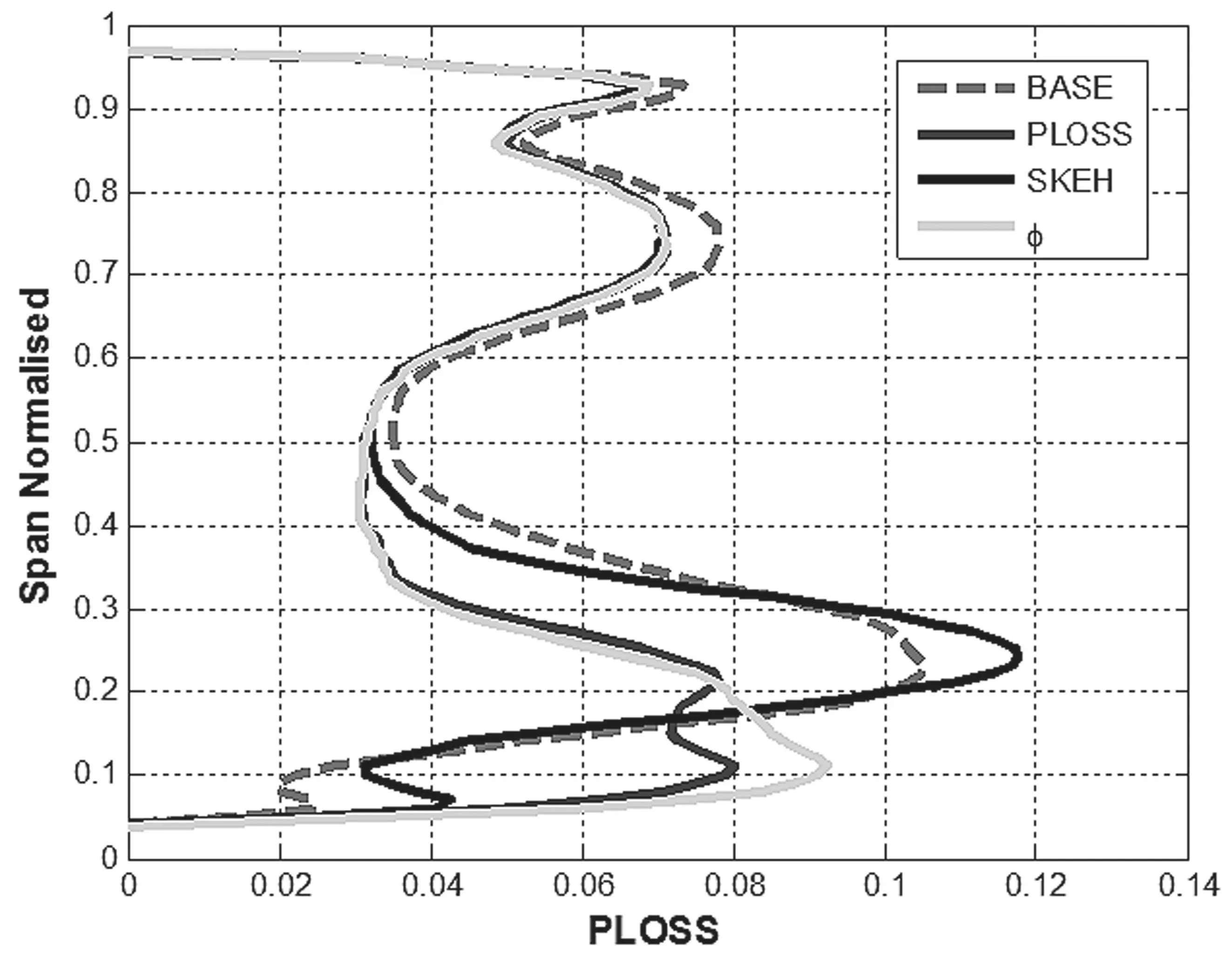
图11 出口总压损失径向分布

图11 给出了四个方案的叶栅出口截面周向平均后的总压损失径向分布。由图11可以清晰看出，在PLOSS和φ结果中，20%～50%叶高范围内总压大幅度减小，并且二次流涡核更贴近下端区，减少了二次流与主流区的掺混损失；而在SKEH优化结果中，下端区通道涡涡核区及贴近壁面区域总压损失均有增大，其余区域基本保持不变。

4.5 SKEH分布对比

SKEH是与二次流损失直接相关的量，其反映了二次动能本身的大小。图12给出了叶栅出口处SKEH分布云图，图13给出了出口SKEH沿径向分布情况。

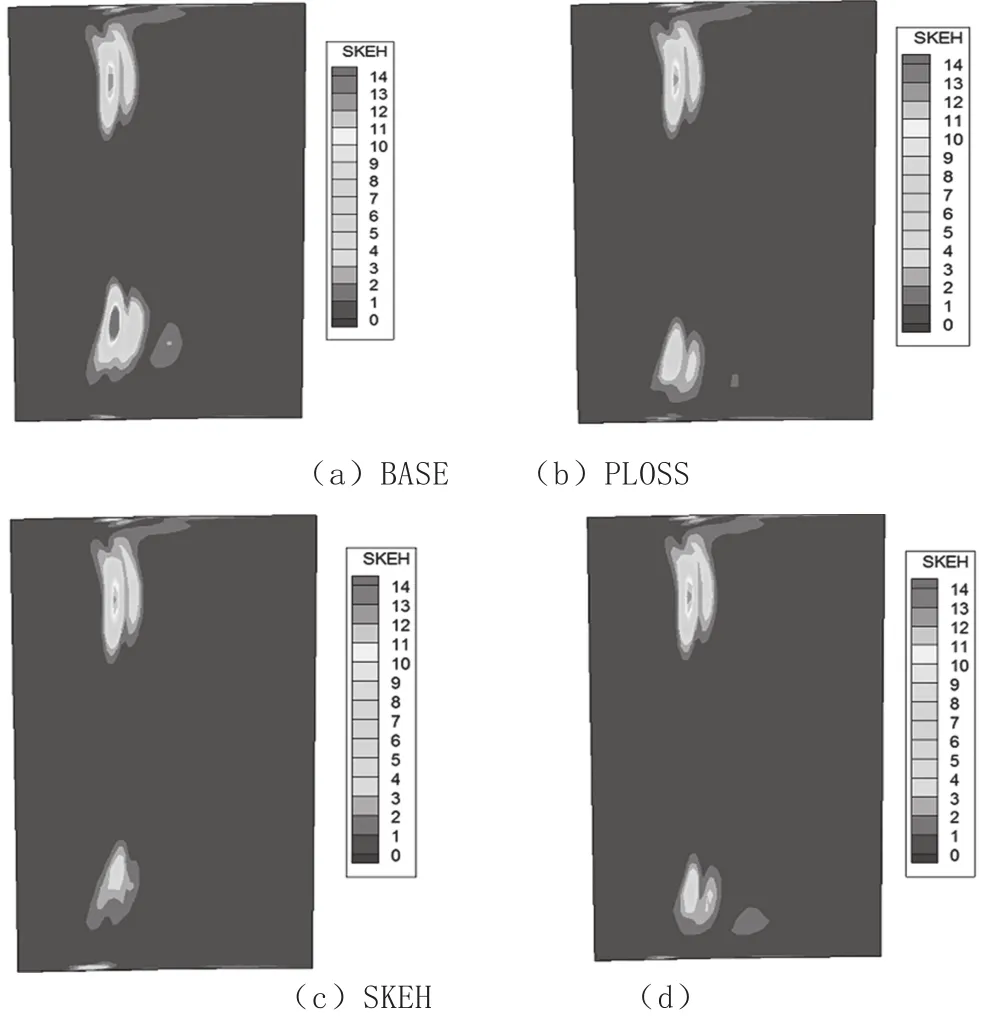
图12 出口SKEH云图

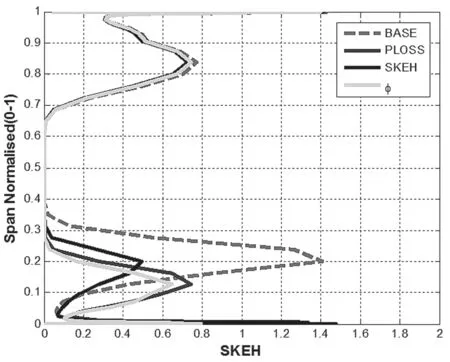
图13 出口总压损失径向分布

由图12、图13可见，相对于基准方案，三个优化方案下出口下端区SKEH均有所减小。其中，SKEH为目标的结果减小幅度最大，φ结果次之，PLOSS结果中SKEH减小的幅度最小。从径向分布上也可看出，PLOSS结果和φ结果中二次动能较大的区域下移，而SKEH结果中径向位置未发生明显改变。

3 结论

本文在某高升力低压涡轮叶栅上开展了非轴对称端壁优化设计，计算时考虑轮缘封严容腔的影响，对不同的优化目标函数进行了研究，包括总压损失、SKEH及组合参数φ，对比获得的详细流场细节，分析得出以下结论。

（1）三个优化方案中，PLOSS和φ目标函数结果总压损失均下降，比BASE方案分别下降7.85%和5.66%，SKEH目标函数结果中总压损失增大，增大了2.92%。三个优化结果中SKEH均降低，分别下降28.3%、36.97%和36.31%。

（2）对比不同优化目标结果的进口等涡量图可以发现，进口轮缘封严出流对端区二次流的发展有重要的影响，进行非轴对称端壁优化时需要考虑容腔效应。

（3）在进行非轴对称端壁造型时，人们不仅要关注通道内的横向压差，近前缘处的造型也需要重点关注。前缘处压力侧上凸吸力侧下凹的造型特征有利于改变轮缘封严出流的方向并形成漩涡特征，在封严出流的作用下，马蹄涡的压力面分支强度被削弱且方向发生改变，被推离相邻叶片的吸力面，从而抑制了通道的发展。

（4）单独采用SKEH作为优化函数时，其优化目标聚焦在削弱通道内的二次动能上，因此遏制了对抑制通道涡有利的封严出流漩涡特征的形成，从而抑制了封严气对二次流发展的影响，不利于削弱通道内流动损失。因此，其不适合单独用来作为非轴对称端壁造型的优化目标函数，可选取总压损失或同时考虑总压损失和SKEH的参数（如组合参数φ等）进行优化。