牛头刨床六杆机构的虚拟样机建模与仿真分析

宋克伟 姚文莉 郝 鑫 李贞靖

（青岛理工大学 理学院，青岛 266520）

牛头刨床是一种金属切削加工设备，利用往复运动的刀具切削固定在机床工作平台上的工件。其主运动为电动机→变速机构→摇杆机构→滑枕往复运动。主运动表现出明显的急回特性，即要求滑枕在工作行程中速度低，工作回程时急速返回，对此，仅凭经验很难对运行时的位移、速度及加速度和作用力的特征进行判断[1-3]。对牛头刨床六杆机构运行时的以上可测参数以图像形式输出，并分析各运动副中的受力就显得非常有必要。

以往对牛头刨床六杆机构的研究主要偏向于对其运动学及优化进行分析。伍平主要针对多体系统建立动力学方程模型并进行数值求解[4]。汤萍等利用实例机构，分析了机械系统的某一角速度建模求解过程[5]。此外，有学者论述了运用ADAMS软件建立牛头刨床机构的几何建模过程，并对其运动学进行仿真分析[6-7]。赵玉成等利用Pro/E对牛头刨床进行了动力学分析并得到各运动副连接处的作用反力曲线[8]。本文基于全局坐标系，利用各构件转动副之间的坐标关系建立滑枕运动至不同位置时的运动学方程，采用分离体法和图解法添加不同工况下的切削阻力对机构进行应力分析，应用ADAMS进行动力学仿真，以贴近工程实际并为多体系统动力学的建模过程提供典型的实例分析。

1 模型的建立

针对一种牛头刨床机构简图，本文建立了直角坐标系，如图1所示。其中，构件1为曲柄，与水平方向的夹角为θ，作为原动件为整个机构提供动力，最终实现构件5的直线往复运动。曲柄BC的连续回转运动带动摆杆AD的往复摆动，通过连杆DE带动滑枕EF作直线往复运动，从而实现刀具G在工件上作切削运动。其中，C1和C2、D1和D2分别为摆杆AD运动至极限位置时同一铰链点的不同状态。

2 运动学分析

2.1 运动方程的建立

平面机构自由度的计算公式为：F=3n-（2pl+ph），在该机构图中n=5，低副数量pl=7，高副数量ph=0，即整个机构自由度数F=1，其自由度数与原动件数目相同，符合机构具有确定运动的条件。

机构简图中摆杆AD与x轴正方向夹角为φ，根据各构件的位置关系可以确定如下坐标关系B（0，l1），C（l1cos，l2-l1sinθ），D（l3cosφ，l3sinφ）。 因 此 矢 量 AC =（l1cosθ,l2-l1sinθ）。

图1 牛头刨床六杆机构运动简图

则夹角φ可表示为：

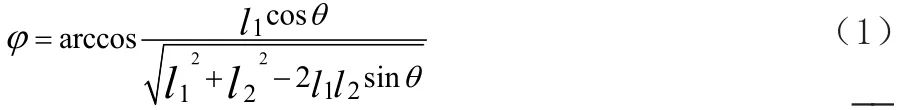
假 设 E点 坐 标 为（x，l5）， 则 矢 量 DE=（x-l3cosφ,l5-l3sinφ）。

因此构件4的长度计算公式为：

整理可得，滑枕位置的函数方程为：

式中，角度φ与角度θ有关，θ与时间t有关。

对式（3）两边求导，得到其速度方程为：

同理，对式（4）两边求导，得到其加速度方程为：

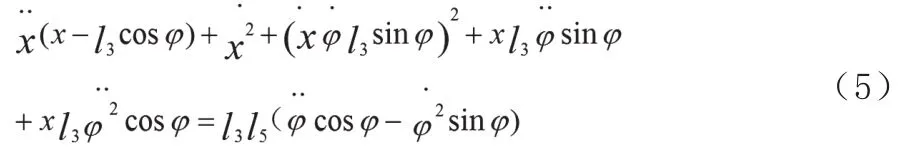
综上分析和计算，同时得到了滑枕EF的位移、速度和加速度运动方程。

2.2 运动学建模与仿真

2.2.1 建模

在ADAMS软件中建立牛头刨床模型时，各构件参数 应 符 合 如 下 要 求：l1=140mm；l2=280mm；l3=600mm；l4=l3/4=150mm；l5=650mm。

摆杆AD的摆动幅度为60°，刨床运动具有明显的急回特性，当曲柄BC以一定角速度逆时针转动，摆杆由右极限位置运动至左极限位置时，刀具G处于工作行程；反之，刀具G处于工作回程。根据以上数据及相关要求，建立模型，如图2所示。

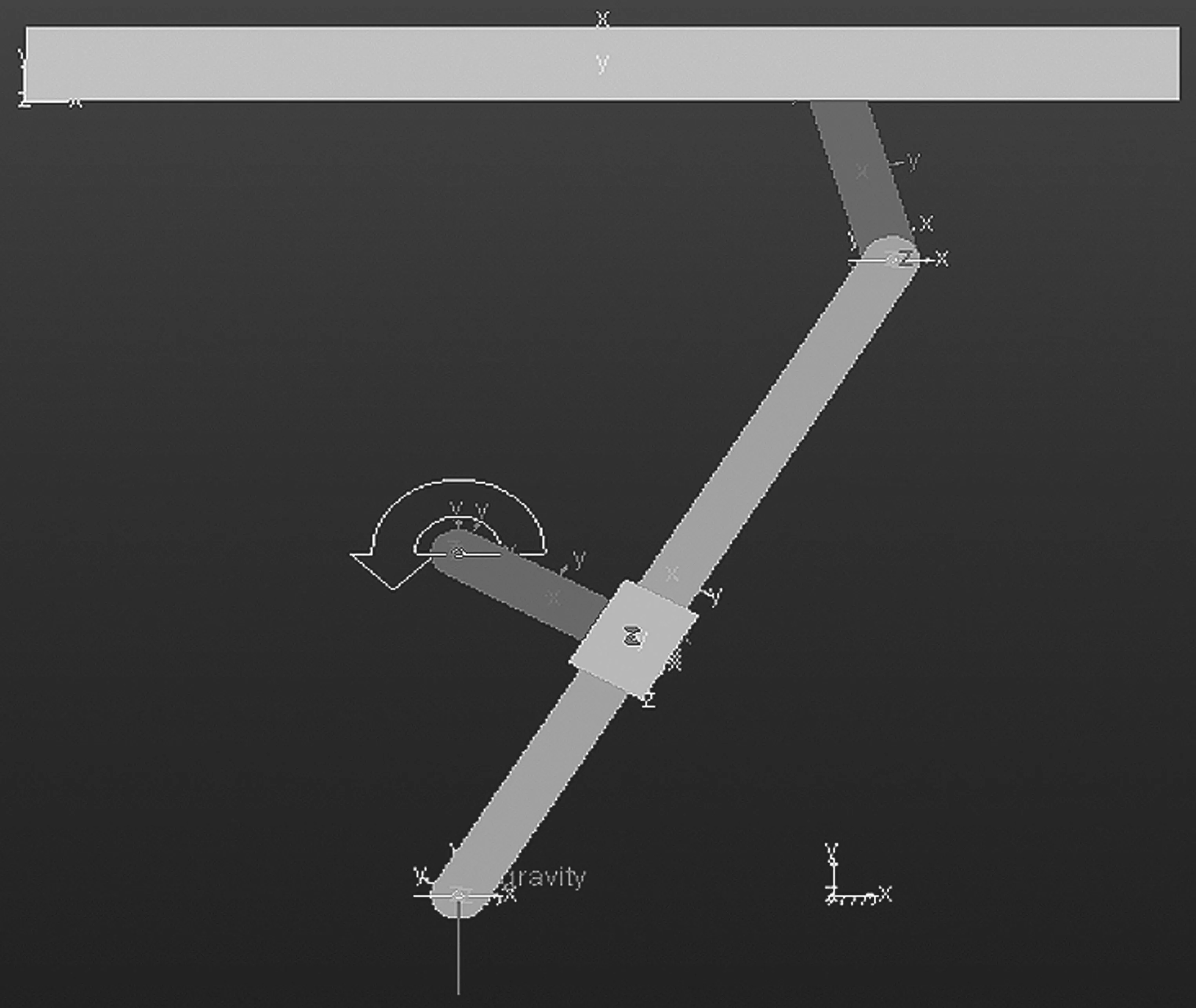
图2 牛头刨床六杆机构虚拟样机模型

2.2.2 仿真及后处理

进入仿真及后处理模块，设置曲柄1的角速度ω=π/6rad/s，即其周期为T=2π/ω=12s，设置仿真时间15s，仿真步数500步进行运动仿真。仿真结束测量曲柄1、摆杆AD的转角，滑枕位移、速度和加速度随时间变化规律，并输出曲线图，如图3所示。

通过对图像的综合分析，笔者发现，滑枕上E点最大位移和最小位移分别为-349mm、259mm，其行程为608mm。当刨床处于工作行程时，曲柄运行角度为θ1，工作回程时运行角度为θ2，θ1＞θ2，并且曲柄角速度ω恒定不变，因此工作回程时速度远远大于工作行程时速度，刨床获得较为明显的急回特征。将刨床尺寸参数分别代入式（3）、式（4）、式（5），其计算数据符合机构运动的特征曲线，仿真具有正确性。

3 动力学分析

3.1 数学模型的建立

根据前述运动学分析可以求得滑枕的惯性力Fi5，若只考虑滑枕质量G5、惯性力Fi5和切屑阻力Fr，可应用图解法和分离体法求解各运动副中的反力和加于原动件上的平衡力偶距。各构件受力如图4所示。

杆组4、5受力情况如图4（a）所示，根据矢量关系列平衡方程如下：

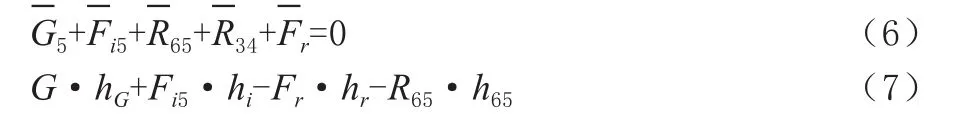
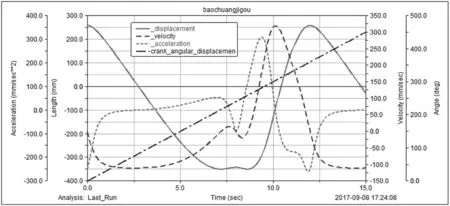
图3 原动件转角与滑枕E点运动曲线

杆组3、4受力情况如图4（b）所示，列出矢量方程为：

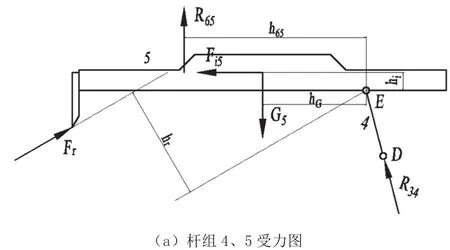
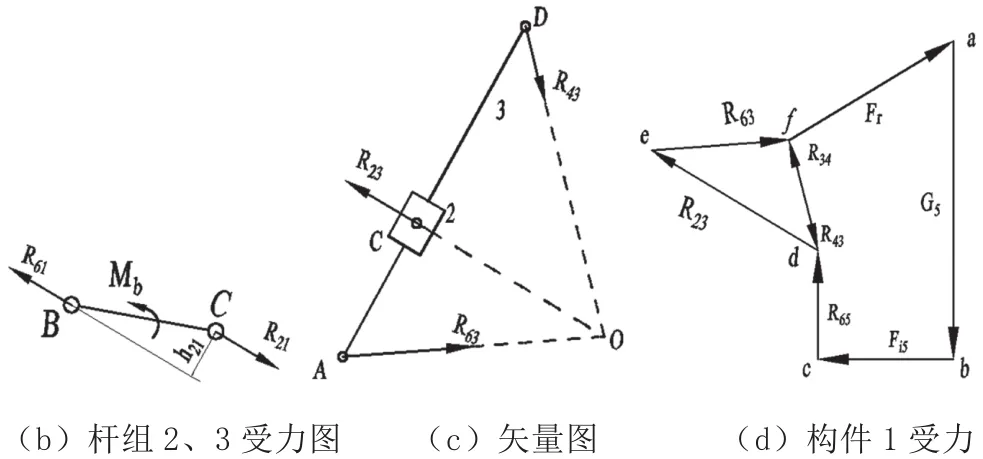
图4 构件受力分析

取一定比例μl按照图解法绘出矢量图，如图4（c）所示。矢量图中各线段长度即代表对应力的比例大小。以构件1为示力体，其受力情况如图4（d）所示，求得平衡力矩Mb=-R21h21，方向与ω相同。

图5 转动副B处约束反力Fx

图6 构件1平衡力矩Md

3.2 动力学建模与仿真

按照已知条件设置构件的质量信息和转动惯量信息，并在刀具G处添加切削阻力Fr，完成动力学建模的设置。仿真后输出支座反力曲线如图5所示，构件1平衡力矩曲线如图6所示。

通过仿真并分析支反力曲线图，发现刨床在工作行程时支反力较大，回程时相对平稳，推得刨床在工作行程时整个机床会产生较大的震动和冲击。刨床处于工作行程时，平衡力矩相对更平稳，回程中力矩波动幅度大且最大力矩出现在切削阻力出现和消失时，符合实际运行需要。

4 结语

对机构进行理论分析和仿真分析，验证了模型的正确性，同时较为直观地展现出刨床处于工作行程时滑枕的速度变化平稳，加速度值也较小，工作回程时速度变化幅度大，加速度值较大，具有明显的急回特性。研究成果可为六杆机构的优化设计提供技术指导，为其他类似机构的运动学和动力学问题的分析提供借鉴。利用虚拟样机技术在概念设计阶段，通过科学理论和计算机语言，对设计阶段的产品进行虚拟性能测试，达到提高性能、降低设计成本和减少产品开发时间的目的。