基于MATLAB与ADAMS的双足步行机器人特性研究

，，，

(昆明理工大学机电工程学院，云南 昆明 650500)

0 引言

双足步行机器人技术的关键就是要实现稳定步行，必须能够像人类一样稳定行走[1]，因此研究双足机器人稳定性和能耗性具有重要意义。第一位给出稳定性精确数学定义的人是俄国学者李雅普诺夫[2]，但该方法不太适用于构造一般的非线性系统，因此只能凭借经验和技巧来处理稳定性问题；Grizzle等人运用庞加莱映射分析了三连杆模型双足机器人的步行稳定性问题[3]；Goswami等人提出了控制质心角动量变化率的3个策略[4]；Vukobratovic重新对ZMP进行定义[5]，这使得ZMP理论日趋完善。Hase等人研究足端轨迹规划对能量消耗的影响[6]；Schiehlen等人用最优控制理论的方法来降低能耗[7]； Uemura[8]，Singh[9]等人通过节能的结构设计来降低能耗。Ahmed[10]等人利用机器人在摆动阶段机械能守恒的特点，设定机器人的目标能量，通过反馈控制使机器人的能量收敛到参考能量范围内从而起到节省能耗作用。

双足机器人稳定性与能耗的研究取得了很大的进步，但是依然存在着很多未解决的问题。在此，以模块化类人机器人为研究对象，在UG中建立了虚拟样机，通过建立稳定性和能耗模型，在ADMAS虚拟样机中以不同的工况对其稳定性、能耗性进行计算分析，并设计实验验证仿真计算的有效性。

1 双足机器人模型建立

1.1 稳定性建模

以模块化类人机器人为物理样机，在 UG 中建立双足步行机器人模型如图1所示。由于将三维模型数据导入到ADAMS会丢失零部件的装配关系，因此模块化类人机器人可直接通过设置材料来确定该模型的质量和转动惯量[11]。

图1 双足步行机器人分析模型

在双足步行机器人的动态行走过程中，对其进行受力分析，其合力并不是时刻都在支撑区域内[12]，因此很难评价双足机器人行走时的稳定性。在ZMP稳定性判据、庞加莱回归映射稳定性理论、质心角动量判据中，由于ZMP稳定性判据可以通过判断双足机器人的关节位置来确定双足机器人行走的稳定性，因此本文采用该判据。ZMP又称零力矩点，使双足机器人在地面反力的合力矩在x，y轴分量为零。在动态行走时，零力矩点ZMP是否落在支撑域内决定了其步行的稳定性。

ZMP原理基本公式为：

(1)

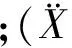
双足机器人行走系统的主要特点为多变量、高阶非线性，与倒立摆系统非常相似，因此采用倒立摆模型对模块化类人机器人的行走运动进行步态规划，将模型近似简化为质量点与无质量腿组成的一级倒立摆模型[13]。经过简化后的双足机器人行走系统模型结构如图2所示，该系统的坐标原点为踝关节旋转中心处。

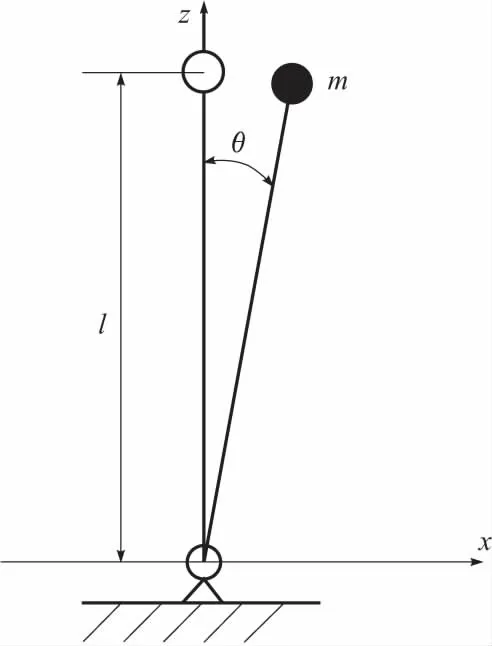
图2 双足机器人倒立摆系统简图

结合一级倒立摆模型，对式(1)进行简化可得：

(2)

xzmpd为理论步态规划x方向上的理论坐标值；yzmpd为理论步态规划y方向上的理论坐标值；m为机器人的总质量；X，Y和Z分别为机器人重心的坐标分量。

通过在足底安装六维力传感器测量相关参数，从而计算出双足机器人X，Y方向坐标值，其计算公式为：

(3)

Xzmpa为仿真过程中X方向的坐标值；Yzmpa为仿真过程中Y方向的坐标值；Txi，Tyi为第i个传感器在X，Y方向的力矩；Fzi为第i个传感器在Z方向的作用力；Xi，Yi为第i个传感器在X，Y方向的坐标。

在设计稳定性能函数时，主要是确定在一定的时间内ZMP坐标仿真值与理论值之间偏差的绝对值，故双足步行机器人稳定系数的计算公式为：

(4)

Kfall_x为双足步行机器人在x方向上的稳定系数；Kfall_y为双足步行机器人在y方向上的稳定系数；N为步数；Ts为每步的周期；ls为单步步长。

1.2 能耗建模

在双足步行机器人能耗的计算中，可以通过测量电源的功耗来计算双足机器人行走的能耗，但是这要在物理样机上才能实现，而且结果容易受到如摩擦力等环境因素的影响。本文通过考虑模块化类人机器人的稳定性，来进行能耗的计算，其理论计算如下。

P=F×V

(5)

P为机器人消耗功率；F为关节行走时的力；V为机器人行走速度。双足机器人步行时，相当于连杆一定程度上的转动，那么：

V=W×R

(6)

V为机器人步行速度；W为关节角速度；R为关节转动半径。

T=F×R

(7)

T为扭矩；F为关节行走时的力；R为关节转动半径。

由式(5)、式(6)、式(7)得：

P=T×W

(8)

通过ADAMS与MATLAB联合仿真，利用PID控制，可以测量出机器人每一个关节的力矩曲线。所以能耗性能目标函数的设计就可以这样计算出来，即关节消耗的能量的总和除以所步行的总时间，算出所有关节单位时间内的功率，计算公式为：

(9)

2 双足机器人特性研究及实验验证

2.1 稳定性分析

通过已规划的各个关节的运动轨迹，以样条文本的方式导入到 ADAMS 中，然后调用样条插值函数AKIMA 规划出虚拟样机每个关节的运动轨迹，并将其输入到相应的关节上进行计算。根据稳定性能函数(式4)，其中步长50 mm，求出不同行走速度(50 mm/s， 100 mm/s ，150 mm/s，200 mm/s， 250 mm/s)和不同摩擦系数(0.1，0.2，0.3，0.4，0.5，0.6，0.7)下双足机器人的Kfall_x和Kfall_y。不同摩擦系数下，Kfall_x和Kfall_y随速度变化的曲线如图3所示。不同速度下，Kfall_x和Kfall_y随摩擦系数变化的曲线如图4所示。

图3 不同摩擦系数下Kfall_x和Kfall_y 随速度变化的曲线

由图3可知，同一摩擦系数情况下，Kfall_x和Kfall_y随机器人行走速度的增加而增大，稳定性变差；相同速度下，Kfall_x和Kfall_y随摩擦系数增大而减小，稳定性变好。由图3可知，摩擦系数大于0.6，X方向与Y方向的稳定性变化不大，行走速度大于200 mm/s，机器人稳定性变得更差，所以该机器人在不同摩擦系数的情况下行走，最高行走速度为200 mm/s时，最低摩擦系数为0.6，双足机器人稳定性较好。

由图4可知，机器人在不同速度的情况下行走，最低摩擦系数0.6时，最高行走速度为200 mm/s，双足机器人稳定性最好。

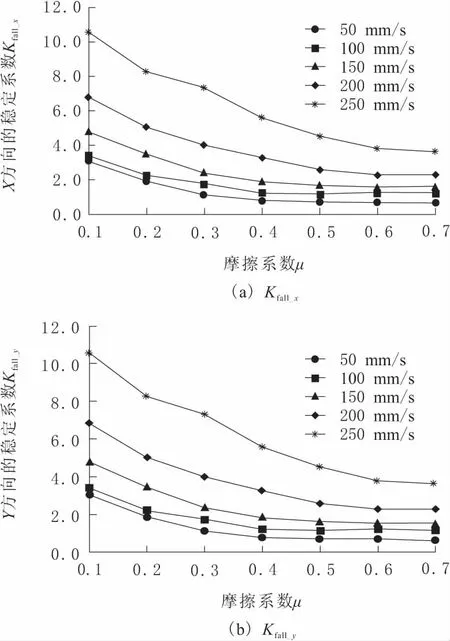
图4 不同速度下Kfall_x和Kfall_y随摩擦

分析XY2个方向上的稳定性参数，可知不同速度都有保持机器人稳定性的最低摩擦系数，低于摩擦系数最低要求，机器人稳定性降低，机器人行走速度过快，稳定性能也会下降。得出本文研究机器人在尽可能提高工作效率且保持稳定的情况下，速度200 mm/s左右速度最佳，而200 mm/s保持稳定最低摩擦系数为0.6。

2.2 能耗分析

根据设计的能耗函数(式5)，在步长为50 mm，单步周期为0.5 s，行走速度为100 mm/s的工况下，绘制能量变化折线图。可得到不同摩擦系数和不同速度下能耗的变化如图5所示。其中，摩擦系数取0.3，0.4，0.5，0.6，0.7；行走速度取50 mm/s，100 mm/s，150 mm/s，200 mm/s，250 mm/s。

图5 能耗变化

由图5可知，同一摩擦系数下，能量都是随速度的增加而增大，当行走速度超过200 mm/s时，能耗速率变得更快，则考虑节能时得保证最高行走速度为200 mm/s；相同速度下，能耗随摩擦系数增大而减少，摩擦系数大于0.6时，能耗消耗变化不大，只有最低摩擦系数0.6才能达到节能效果。所以本机器人从工作的高效性考虑，结合稳定性计算分析结果，机器人最高步行速度200 mm/s时保证最低摩擦系数为0.6，是机器人所能达到在保持能耗增速变化不大下的最佳条件。

2.3 实验验证

在能耗实验中，通过给机器人安装电流传感器，并检测每个电机在不同速度下的实际工作电流，根据电机的额定电压估算每个电机在不同速度下的工作功率，从而估算出机器人整体在不同速度下的工作功率。以左下肢为例，其接线和电流检测如图6所示。

图6 速度100 mm/s时左下肢电流检测

以摩擦系数为0.6，额定电压为12 V，测出不同行走速度下各位置电流值和功率值如表1所示。表1中，左右相同位置电流接近，所以只列出左侧，即总电流是左侧电流2倍。

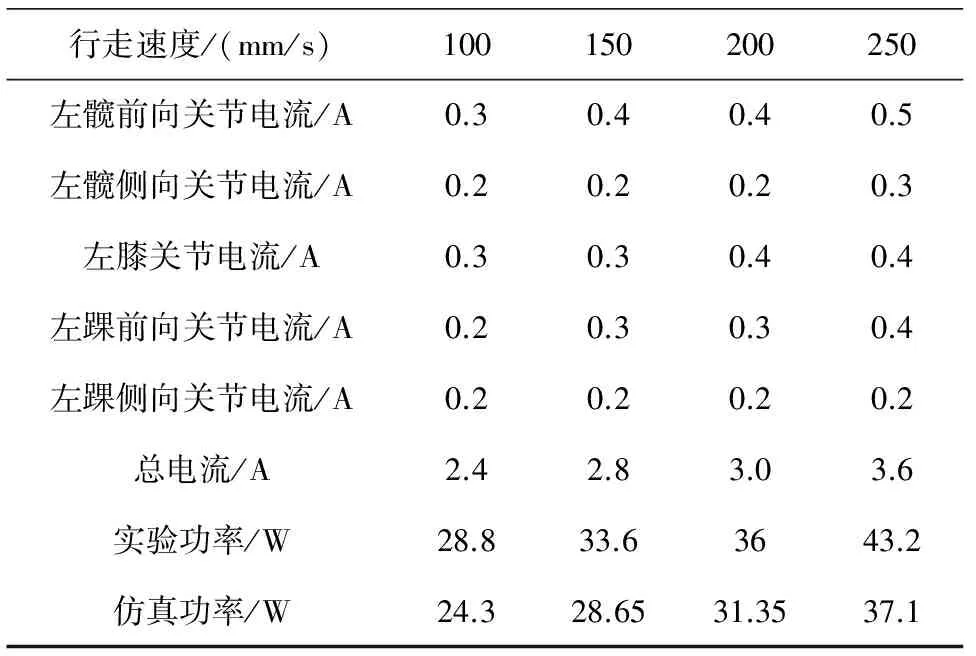
表1 不同行走速度下的电流值和功率值

由表1可知，仿真值较实验值整体偏低但是最大误差为15.6%，同时可以看出机器人步行速度超过200 mm/s，能耗消耗加快。结合稳定性与能耗分析，验证了仿真200 mm/s左右为该模块化类人机器人能耗比较好的速度，从而验证仿真及设计能耗函数的合理性。

3 结束语

建立了双足机器人的稳定性模型，计算了不同速度及摩擦系数下的稳定性能参数，得出模块化类人机器人在保持稳定的情况下，速度为200 mm/s左右最佳，而最低摩擦系数为0.6。

建立了双足机器人能耗模型，针对双足步行机器人的能量消耗，从该机器人工作的稳定性与能耗考虑，得出该双足机器人行走速度为200 mm/s，摩擦系数为0.6时，其性能最佳。

通过能耗实验，验证了本文设计稳定性函数、能耗函数的合理性，以及仿真结果的有效性。

[1] Harada K, Kajita S, Kaneko K, et al. An analytical method on real-time gait planning for a humanoid robot[C]//IEEE/RAS International Conference on Humanoid Robots,2004:640-655.

[2] 曾癸铨.李雅普诺夫直接法在自动控制中的应用[M].上海:上海科学技术出版社,1985.

[3] Grizzle J W, Abba G, Plestan F. Asymptotically stable walking for biped robots: analysis via systems with impulse effects[J]. IEEE Transactions on Automatic Control,2001,46(1):51-64.

[4] Goswami A, Kallem V. Rate of change of angular momentum and balance maintenance of biped robots[C]//IEEE International Conference on Robotics and Automation, 2004:3785-3790.

[5] Vukobratovic M, Juricic D.Contribution to the synthesis of biped gait[J].IEEE Transactions on Biomedical Engineering, 1969, BME-16 (1):1-6.

[6] Hase T, Huang Q.Energy-efficient trajectory planning using inequality state constraint for biped walking robot with upper body mass[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems,2006:5913-5918.

[7] Schiehlen W,Iwamura M.Minimum energy control of multibody systems utilizing storage elements[C]//ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference,2009:1919-1926.

[8] Uemura M, Lu G, Kawamura S, et al.Passive periodic motions of multi-joint robots by stiffness adaptation and DFC for energy saving[C]//SICE Annual Conference, 2008:2853-2858.

[9] Singh S P, Dutta A, Saxena A. Design of a biped robot with torsion springs at the joints for reduced energy consumption during walk[C]// ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference,2009:987-992.

[10] Ahmed I, Aris I B,Marhaban M H,et al.Energy consumption analysis procedure for robotic applications in different task motion[J]. IOP Conference Series: Materials Science and Engineering, 2015,99(1):1-8.

[11] 李军,邢俊文,覃文洁,等.ADAMS实例教程[M]. 北京:北京理工大学出版社, 2002.

[12] 王春雨.仿人型机器人步行稳定性研究和步态设计[D].上海:上海交通大学,2011.

[13] 李建.双足机器人的倒立摆模型及其控制研究[D].济南:山东大学,2010.