基于改进型灰色马尔可夫模型的公路货运价格预测

汤银英，李龙，秦阳

（1. 西南交通大学，交通运输与物流学院，成都610031；2. 综合交通运输智能化国家地方联合工程实验室，成都610031）

0 引 言

近几年随着公路运输在我国运输市场中占有的份额不断增大，公路货运对我国物流行业的影响也越发深远。公路货物运输价格是反映公路货运市场供需关系的“晴雨表”，也是合理配置公路货运市场资源的基础性手段[1]。探究公路货运价格变化规律，把握运价变化趋势，对于政府调节公路货运市场发展及运输企业适应市场变化都有着重要意义。

公路运输市场化程度较高，其货运价格随市场波动变化的频度与幅度都比较大，这使得公路货运价格预测工作较为困难，预测精度普遍不高。另外，由于公路货运价格受到市场供需状况、油价、政府相关政策、车辆保有量等多种因素共同影响，而这些影响因素的信息获取困难较大，所以基于因果关系的预测方法很难适用。研究发现一些传统预测方法诸如回归分析法、灰色模型等在进行公路货运价格预测时虽然可以克服影响因素信息缺乏的困难，但是存在对历史数据有用信息提取不足，对货运价格波动曲线的拟合程度不高等缺点，使得预测结果很不理想[2]。灰色马尔可夫组合模型能够针对信息缺失且短期波动剧烈的时间序列数据进行预测，并且预测效果良好，但其预测精度仍存在进一步提升的空间。因此本文对灰色马尔可夫模型加以改进，提高了公路货运价格数据的预测精度[3]。

1 灰色马尔可夫组合模型基本思想

公路货运系统中影响公路货运价格的因素众多，但由于人们的认知能力有限，难以合理确定公路货运价格变动的上涨因素与下降因素，以及引起运价变化的主要因素与次要因素等。因此，可以将公路货运系统视为一个没有清晰因果关系的、信息不完全的灰色系统，进而用灰色理论加以研究。灰色理论中的单序列一阶线性微分方程预测模型（也称为灰色GM（1，1）模型）无需从影响公路货运价格的众多因素中进行主要因素的比选，也无需对各个影响因素单独进行数据的调查和分析，因此适用于信息不全的数据序列的预测，并且对历史数据中存在的长期增长（或减少）的趋势量（即残差）能进行较为精确的预测，因而具有简单适用的特点。但是灰色GM（1，1）预测模型要求对历史数据累加后生成的数列具有指数规律，而公路货运价格波动频率和幅度都比较大，采用单一的GM（1，1）预测模型则会自动过滤掉这种随机性波动，无法对历史数据中的有用信息进行充分提取[4-6]。

另外，公路货运系统是一个动态的系统，货运价格作为公路货运这一动态系统的特征量，它的变化会呈现出随机过程的特点，而马尔可夫链可描述这种具有随机波动特点的动态过程。与灰色GM（1，1）模型相比较而言，马尔可夫过程则可以实现对历史数据中的状态转移信息进行充分的提取，并且通过状态转移概率矩阵来体现系统的内在规律性，适用于随机波动性较大的非平稳数据序列的预测。

将上述两种模型结合后形成了灰色马尔可夫模型，采用灰色预测模型来揭示公路货运价格变化的总体趋势，然后采用马尔可夫链来确定不同状态间的转移规律，从而使得灰色马尔可夫模型兼具二者的特点，对波动性较强的数据的预测更加精准[7-9]。

2 构建改进型灰色马尔可夫模型

在改进型灰色马尔可夫建模过程中，首先，建立灰色GM（1，1）模型进行预测，将灰色预测结果作为马尔可夫过程的状态区间划分的依据；然后，计算出各状态区间的转移概率，构建状态转移概率矩阵，得出灰色马尔可夫模型以及改进型灰色马尔可夫模型预测结果；最后，进行预测精度检验，以便于评定预测模型的预测效果。

2.1 建立灰色GM（1，1）模型

（1）对历史数据进行一阶累加，生成累加数列：

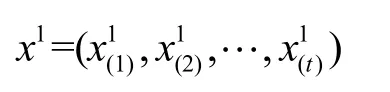
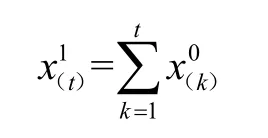
其中，a、u分别为发展系数和灰色作用量，a的有效区间为（-2，2）。

（3）对累加生成数据做均值生成向量B与常数向量Yn，即

（4）记a，u构成的矩阵为，利用最小二乘法求解灰参数，则

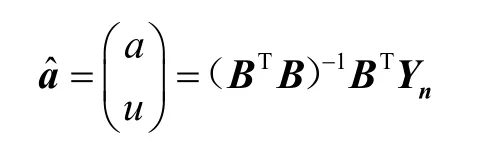
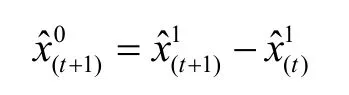
2.2 建立灰色马尔可夫模型

（1）状态区间划分

以公路货运价格实际值与GM（1，1）模型预测值的相对比值p的取值范围s为依据，进行马尔可夫状态区间的划分，将p的取值范围等长度划分为n个区间，得到n+1个状态分界值s=(s1,s2,…,sn+1)，其中n为状态区间个数。

则状态区间Ei具体划分如下：

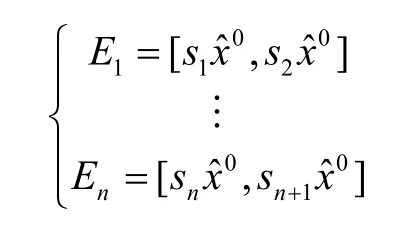
（2）构建k步状态转移概率矩阵

数据序列由状态Ei经过m步转移到状态Ej的概率记为p(k)ij，则

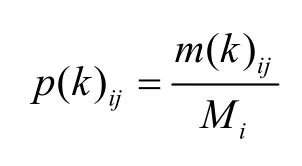
记k步状态转移概率矩阵为p(k)，则

利用状态k步转移概率矩阵p(k)，可以计算出转移至状态区间Ei=(E1,E2,…,En)的对应概率为Pi=(P1,P2,…,Pn)，将Pmax所对应的状态区间Emax作为最后所处的状态区间。

2.3 建立改进型灰色马尔可夫模型

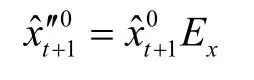
其中，状态转移期望：

其次，个人考核是关键。以团队为单位进行考核虽为重点，但如果将它作为课程考核的唯一标准，则有失公平，可能对个人学习积极性、团队的学习态度和协作精神产生负面影响。

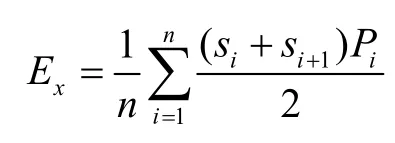
2.4 预测精度判定

最后需要对预测结果分别进行精度评定，评定步骤如下：

（2）对照精度检验表（见表1），进行预测精度评定。

表1 精度检验对照表Tab.1 Model precision table

3 公路货运价格预测实证分析

本文以成都至南昌的公路运输周价格作为研究对象，采集了该通道上2015年8月5日至2016年9月28日期间59周的公路运输周价格数据，选择前46周的数据作为原始数据，对该通道2016年7月6日至2016年9月28日期间13周的公路运输周价格进行预测，见表2。

表2 成都至南昌公路运输周价格表Tab.2 Highway freight transportation price from Chengdu to Nanchang

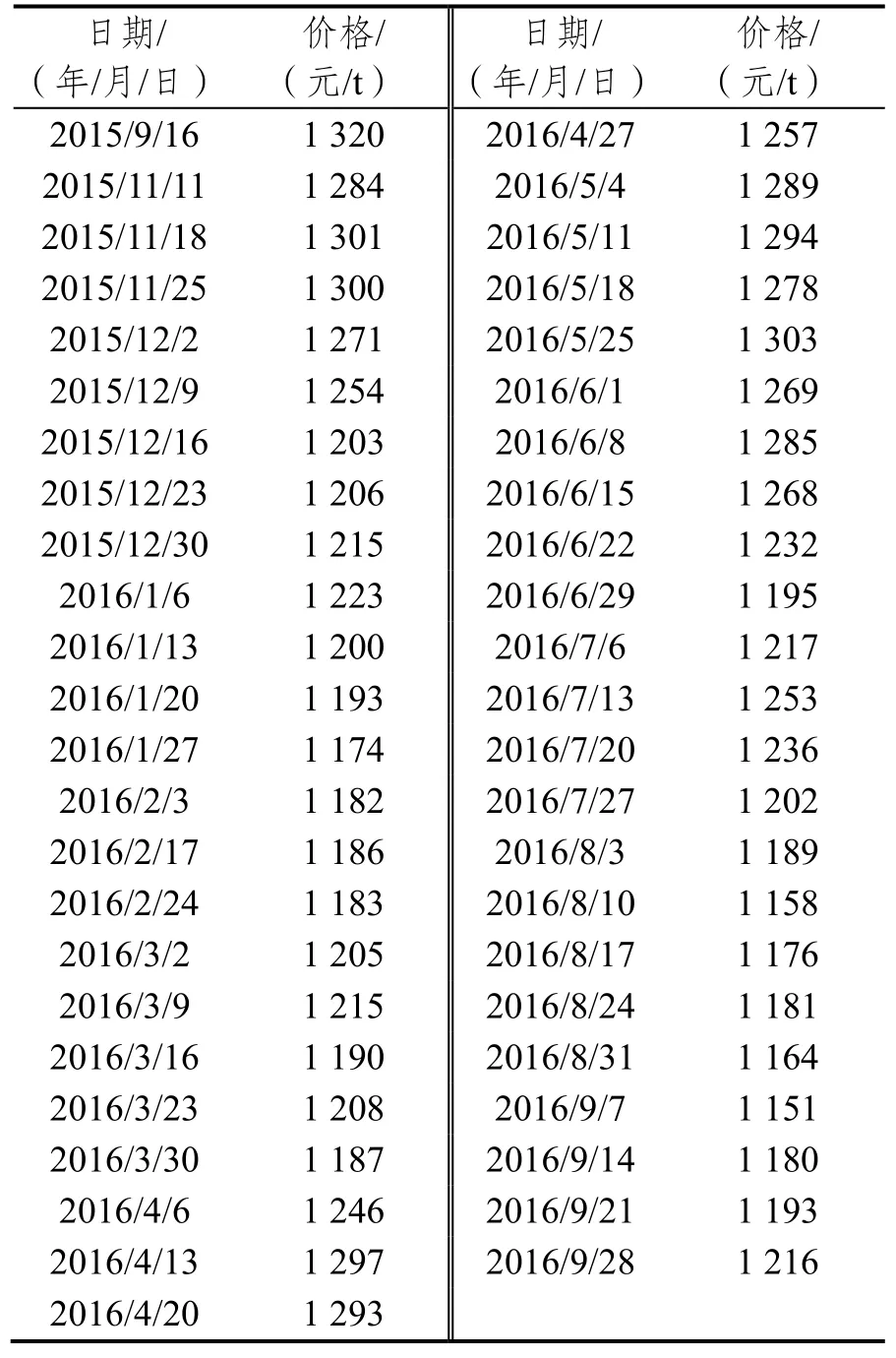
续表2

3.1 进行灰色GM（1，1）模型预测

建立原始序列：

x0=(1223 ,1200,…,1195)，n=25

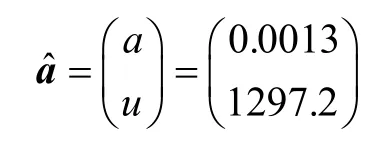
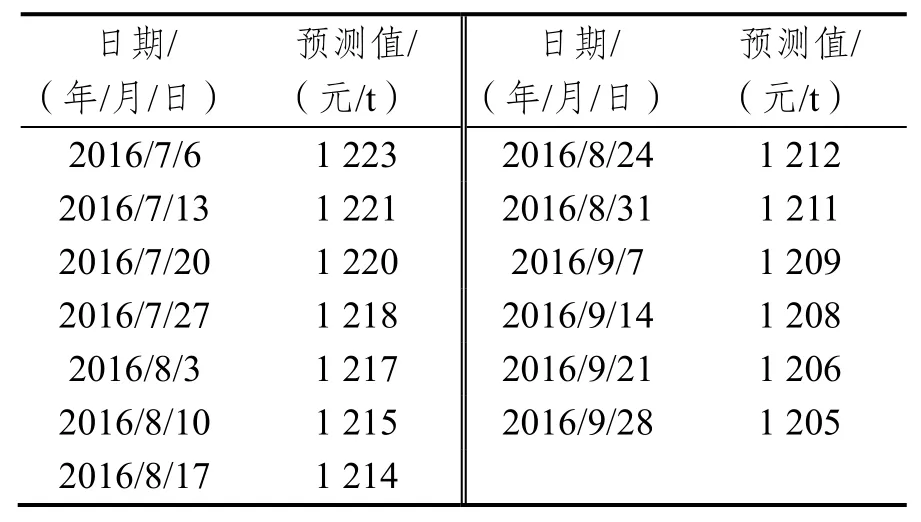
表3 灰色GM（1，1）模型预测值Tab.3 The GM（1，1）prediction results

3.2 进行灰色马尔可夫模型预测

（1）确定状态区间

公路货运价格实际值与GM（1，1）模型预测值的相对比值p的取值范围为s=[0.92，1.12]，等长度划分为四个区间，则各个状态对应的区间分布如表4所示。

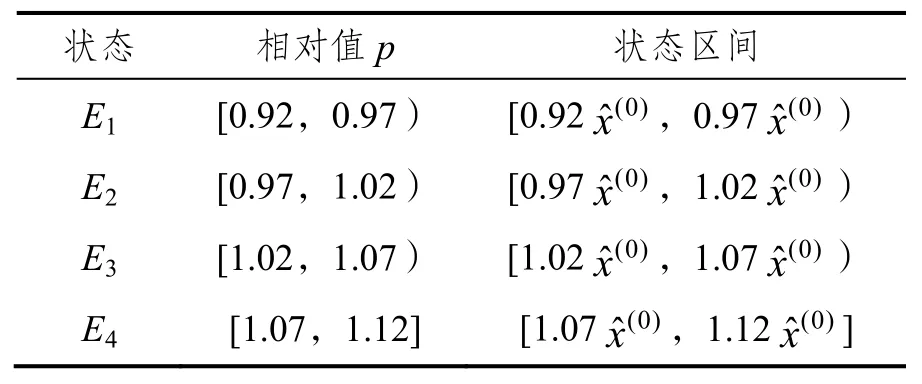
表4 状态区间划分表Tab.4 Feasible state ranges

（2）计算状态转移概率矩阵

分别计算k（k≤4）步转移矩阵：

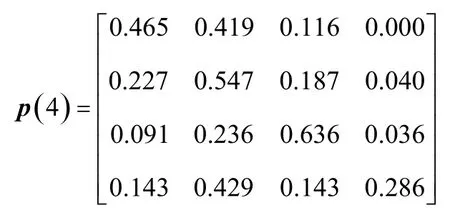
以2016年7月6日成都至南昌的公路货运价格为例进行预测，状态转移区间预测过程如表5所示。

表5 状态区间预测计算表Tab.5 State transition table (Gray-Markov)

最终预测结果见表6。

表6 灰色马尔可夫模型预测值Tab.6 The Gray-Markov predictions

3.3 改进型灰色马尔可夫模型预测值

同样，以2016年7月6日的成都至南昌的公路货运价格为例进行预测，预测结果如表7所示。

表7 状态区间转移期望计算表Tab.7 State transition table (improved Gray-Markov)

表中，

计算改进型灰色马尔可夫预测值，预测结果如表8所示。

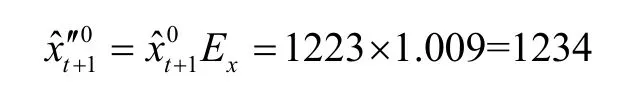
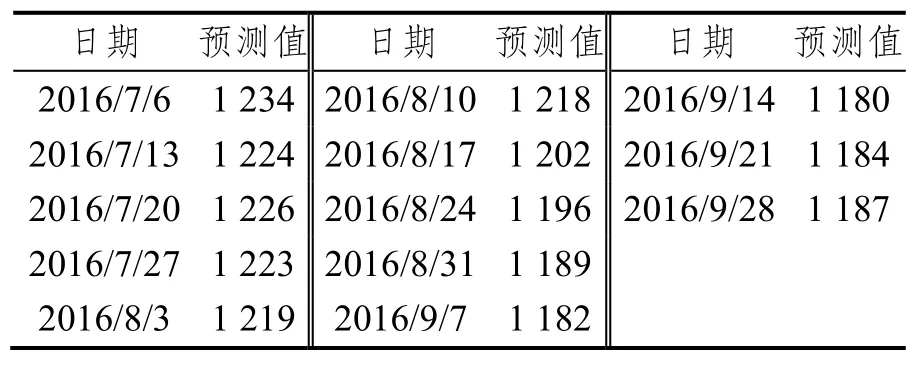
表8 改进型灰色马尔可夫预测值Tab.8 The improved Gray-Markov predictions

3.4 预测精度判定

将2016年7月6日至2016年9月28日期间13周的公路运输周价格预测值与实际值进行比对，计算出相对误差q（x）分布如表9所示。

按照精度检验对照表进行预测精度的评定：在灰色模型的预测结果中，有2个预测精度达到Ⅰ级，9个为Ⅱ级，1个Ⅲ级，平均相对误差2.48%；在灰色马尔可夫模型的预测结果中，同样有2个预测精度达到Ⅰ级，9个为Ⅱ级，1个Ⅲ级，平均相对误差2.58%；而在改进型灰色马尔可夫模型的预测结果中，则有3个预测精度达到Ⅰ级，8个为Ⅱ级，1个Ⅲ级，平均相对误差2.11%。

表9 相对误差q（x）分布表Tab.9 Distribution of the relative error q(x)

最后，将灰色马尔可夫模型的状态区间以及预测曲线走势绘制在图1中。

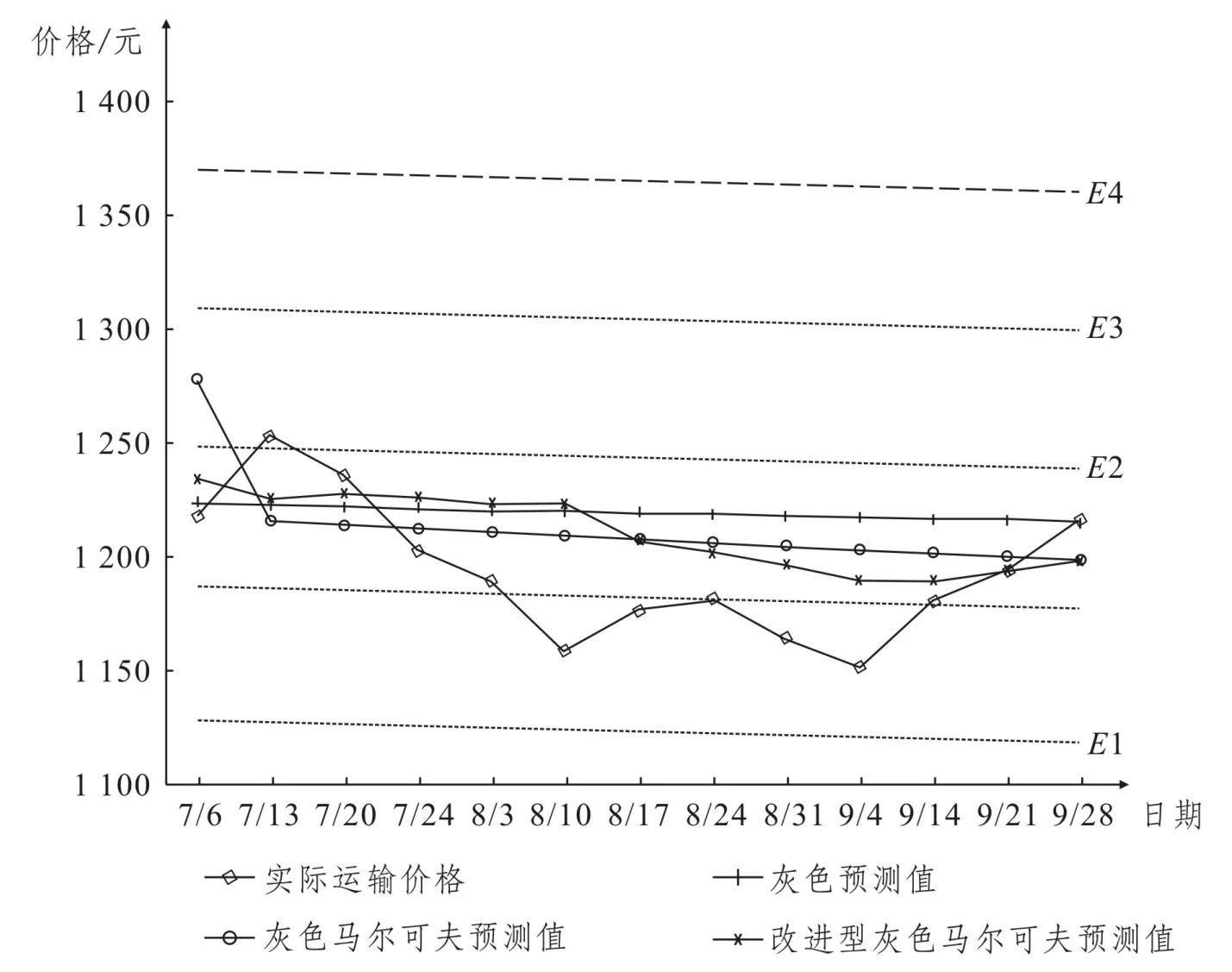
图1 预测曲线对比图Fig.1 Comparison of the predicted results

4 结 论

本文在灰色马尔可夫模型中引入状态转移期望的概念，新构建出改进型灰色马尔可夫预测模型。在对2016年7月6日至2016年9月28日的成都至南昌公路运输周价格的预测结果中，改进型灰色马尔可夫模型预测结果的精度等级更高，预测相对误差更低，说明改进后的灰色马尔可夫模型预测精度获得了明显提升。另外，在预测曲线对比图1中，可以看出预测周期内的公路货运实际价格大多处于E1、E2低状态区间，说明2016年7月6日至2016年9月28日期间的公路货运价格一直处于低位，而改进后的灰色马尔可夫模型预测曲线对价格的这种下降趋势反映的更明显，更符合公路货运价格随市场波动变化的实际。

[1] 周荣康，徐永，李若灵. 基于灰色残差GM（1，1）模型的道路交通量预测的研究[J]. 交通运输工程与信息学报，2008，6（3）：49-53.

[2] 汤银英，李龙. 基于Holt-Winters模型的铁路月度货运量预测研究[J]. 交通运输工程与信息学报，2017，15（2）：1-5，13.

[3] 沈家军，王炜，陈峻. 基于灰色马尔可夫模型的近期公交客流量预测[J]. 公路交通科技，2007，9：120-123.

[4] 顾敬岩，吴群琪. 我国公路货运市场价格的演进趋势、问题及对策[J]. 交通运输系统工程与信息，2013，6：191-197.

[5] 林岩，陈帅，陈燕，等. 道路交通事故的灰色马尔科夫预测模型与算法[J]. 武汉理工大学学报：交通科学与工程版，2013，37（5）：924-928.

[6] 刘宗明，贾志绚，李兴莉. 基于灰色马尔科夫链模型的交通量预测[J]. 华东交通大学学报，2012，29（1）：30-34.

[7] 周盛世，杨丽红，黄永强. 融合灰色理论与马尔科夫链的青岛市物流需求量预测[J]. 企业经济，2011，30（10）：117-120.

[8] 崔勇，王川，陈小龙，等. 基于灰色马尔科夫预测模型的中长期电力负荷预测[J]. 现代电力，2011，28（3）：38-41.

[9] 高阳，谭阳波.基于新维无偏灰色马尔科夫预测模型的中长期能源消费预测[J].统计与决策，2007（22）：55-57.