通胀环境下基于CEV模型的最优再保险-投资问题

，，

(安徽工程大学 数理学院，安徽 芜湖 241000)

再保险可以帮助商避免潜在的巨大损失，而投资能使保险公司实现其管理目标．因此再保险-投资对保险商来说是两个重要的问题．保险市场中的再保险-投资问题越来越引起学者们的重视，关于此类问题的研究也越来越多.Browne[1]最先研究了Lundberg风险模型，给出了保险商终端财富的指数效用最大化和破产概率的最小化．Bauerle[2]首次提到了“比例再保险”这一再保险名词，并且很好地解决了相关的均值-方差问题.Wang[3]等在均值-方差准则以及常弹性绝对风险厌恶(CRRA)效用情形下有效地运用鞅方法研究了最优投资组合问题．Hipp[4]等,Promislow[5]等研究了最优再保险和投资问题，以及怎样来降低保险人破产的概率．Liang[6]等在一个不可测的马尔可夫调制的复合Poisson风险模型中讨论了最优再保险与投资问题．之后，Lin[7]等和Gu[8]等分别应用常方差弹性模型(CEV)来研究最优比例再保险跳扩散风险过程．Li[9]等在均值-方差准则下开始使用Heston模型来研究最优比例再保险和投资问题．在Heston模型下的跳-扩散风险过程，Zhao[10]等考虑了保险商最优超额赔损再保险以及投资问题．基于Heston模型下的默认市场，Zhu[11]等讨论了保险商最优再保险和投资问题．

以上诸多问题的研究中并未考虑通货膨胀情形，而真实市场环境下通胀对投资决策起到了一定的作用.通货膨胀是指在一段给定的时间内，给定经济体中的物价水平普遍持续增长，从而造成货币购买力的持续下降.现如今，通货膨胀已经存在于生活的方方面面，会直接影响投资者投资消费.Munk[12]等考虑了通胀环境下，一个可投资于现金、名义债券和股票的幂效用投资者的最优资产配置问题.Kwak[13]等在通胀环境下，运用鞅方法给出了一个家庭的最优消费、投资和人寿保险决策.Guan[14]等利用CARA效用函数考虑了通胀的最优再保险和投资策略.国内学者的许多文章也考虑了通胀对投资组合的影响.费为银[15]等在Knight不确定和通胀环境下研究了最优投资消费问题，考虑了消费投资中通胀波动率的影响.

在Gu[8]等的基础上进行推广，利用杨鹏[16]折现的方法引入了通胀因素，考虑通胀环境下保险商最优再保险-投资问题.运用动态规划原理，通过求解HJB方程，获得值函数的解析解以及关于保险商的最优再保险-投资策略．将综合考虑通货膨胀环境下基于CEV模型的最优再保险-投资策略问题，最后使用Matlab软件进行数值模拟，分析通胀波动率等参数对最优再保险-投资的影响.

1 模型建立

1.1再保险市场

根据经典的Cramér-Lundberg模型，保险商在时刻t的盈余水平用P(t)表示：

(1)

通过期望值原理可知，c=(1+η)λμ∞,其中η>0是相关的再保险安全负荷系数.

其中，保费率:

这里θ表示再保险商的安全负荷系数，为了再保险市场无套利，要求θ>η.根据Grandell[17]可知，盈余水平P(a)可近似表示为：

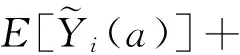
(2)

其中W0(t)是标准布朗运动.

考虑超额赔损再保险：

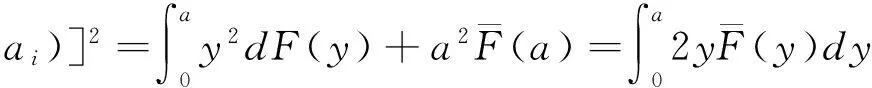
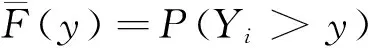
dR(a)(t)=[θμ(a(t))+(η-θ)μ∞]dt+σ(a(t))dW0(t).

(3)

1.2 金融市场

假设金融市场中存在以下两种资产.

无风险资产B(t)价格方程满足：

dB(t)=RB(t)dt,

其中R是确定性的无风险利率.

风险资产S(t)价格方程满足以下CEV模型：

dS(t)=μsS(t)dt+σsS(t)β+1dW(t),

其中μs(μs>R)是风险资产平均收益率，σsS(t)β+1表示一个瞬时波动率.

假设通胀变化率满足：

dL(t)=L(t)[μpdt+σpdW(t)].

其中,μp,σp分别表示通货膨胀率的预期增长率和预期波动率.

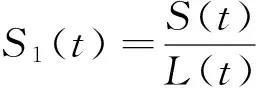
μp-σpσsSβ)dt+(SβσS-σP)dW(t)].

假设保险商在上述通货膨胀影响下进行投资，其中在t时刻投资在风险资产的现金流为π(t)，于是保险商的盈余过程满足下面的随机微分方程：

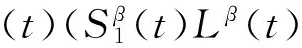
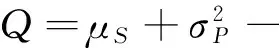
2 最优再保险-投资策略

在上述模型的基础上，以财富期望效用最大化为目标，寻求最优再保险-投资策略.假设收益函数为：

Hπ(t,x,s1)=E[u(X(T))|X(t)=x,S1(t)=s1,L(t)=l],

H(t,x,s1)=supHπ(t,x,s1,l),

目标是最优策略π*∈π使H(t,x,s1,l)=Hπ*(t,x,s1,l).

设保险商财富效用采用幂效用函数：

(4)

其中γ为幂效用下的风险厌恶因子.

易知该问题的HJB方程为：

(5)

由一阶条件可得：

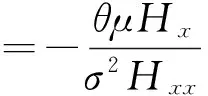
(6)

(7)

将式(6)，式(7)代入式(5)整理得：

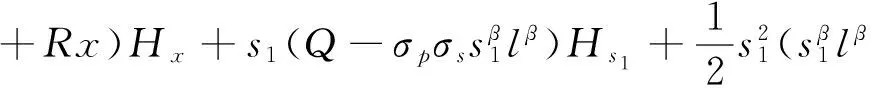
(8)

考虑幂效用函数式(4)，可设

(9)

此时式(9)各偏导如下：

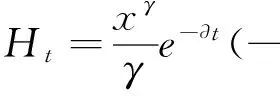
将以上得到的各偏导代入式(8)可得：

(10)

消除式(10)中对x的依赖，得到：

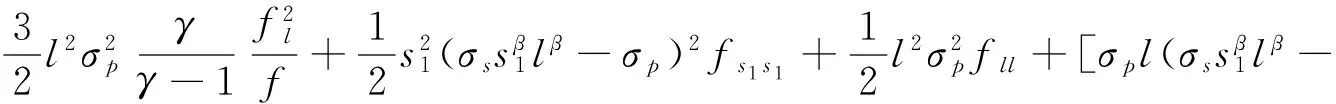
(11)

假设式(11)解的结构：

f(t,s1,l)=u(t,s1,l)1-γ,u(T,s1,l)=1.

(12)

则式(12)各类偏导如下：

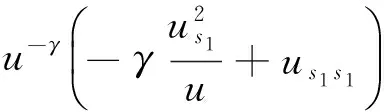
(13)

将式(13)代入式(11)得：

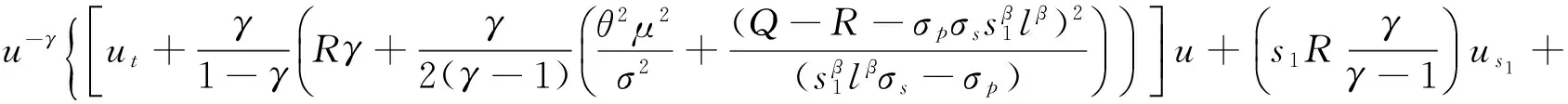
(14)

令式(14)大括号里算式等于0，则可得到关于u(t,s1,l)的微分方程：

(15)

假设式(15)形式如下：

u(t,s1,l)=exp{A(t)+B(t)s1+C(t)l}.

(16)

边界条件A(t)=0,B(T)=1,C(T)=1.则式(16)各偏导如下：

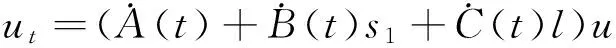
us1s1=B2(t)u,ul=C(t)u,ull=C2(t)u,us1l=B(t)C(t)u.

(17)

将式(17)代入到式(15)中，得到：

(18)

消除式(18)中关于s1,l的影响，可以得到如下3个方程：

求解以上3个等式可得：

其中，

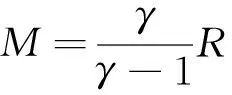
最后，得到最优再保险投资策略为：

3 数值模拟

为了更好地分析财富水平和通胀因素对最优再保险和投资的影响，利用MATLAB进行了数值模拟，并对所得最优策略进行分析.盈余水平波动率对最优再保险策略的影响如图1所示．图1中参数为：θ=0.1,γ=0.3,x=1.图1是由两种不同的线组成，这是考虑了在其他参数不变的情况下，仅仅考虑盈余水平波动率的改变，造成的最优再保险策略的变化．由图1可知，再保险策略随着系数σ的增加而减小，对保险商来说就存在更低的保险风险，因为保险商将更多的风险转移给再保险商来得到最优的一个财富.

安全系数θ对最优再保险策略的影响如图2所示.图2中参数为：θ=0.1,γ=0.3,σ=0.15,x=1.θ意味着对冲保险风险的成本，θ越高，保险商所用来对冲保险风险的成本就越高，θ越大，再保险公司的保费收入越大，即保险公司进行更多的再保险，也就是进行更多的再保险策略.所以再保险策略和再保险商安全系数θ之间是正相关的.

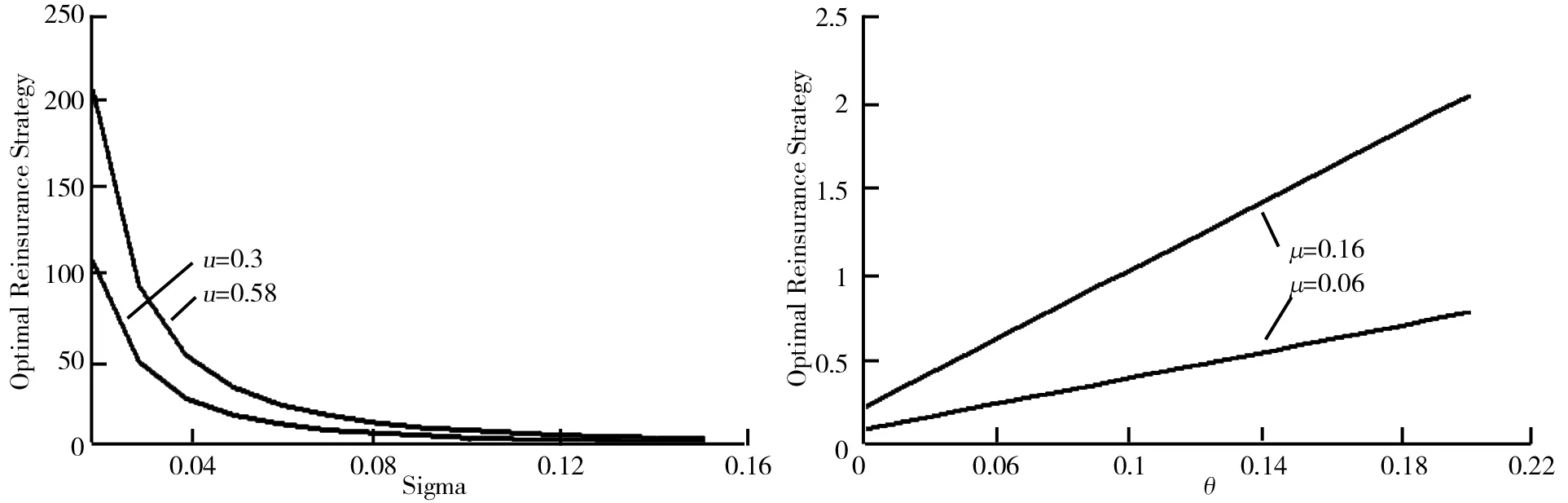
图1 盈余水平波动率对最优再保险策略的影响图2 安全系数θ对最优再保险策略的影响

图3 通胀系数对最优投资策略的影响

4 小结

在通胀环境下，对保险商的风险资产进行通胀折现，并给出了财富过程的动力学方程，建立了相应的HJB方程.通过求解方程，获得值函数的解析解和最优再保险-投资策略；最后，通过数值模拟给出通胀对最优投资的影响. 研究所得结果和相应分析为保险商在金融市场中再保险-投资提供一定的理论指导．

在现有工作的基础上考虑通胀对保险商最优再保险投资策略的影响，保险商可以投资于风险资产和无风险资产，投资更加多样化.在进行讨论时并没有考虑交易费用和税收等摩擦成本，后面将进一步讨论带摩擦成本情况下保险商最优再保险-投资问题.

[1] S BROWNE.Optimal investment policies for a firm with a random risk process:exponential utility and minimizing the probability of ruin[J].Mathematics of Operations Research,1995,20(4):937-958.

[3] Z WANG,J XIA,L ZHANG.Optimal investment for an insurer:the martingale approach[J].Insurance:Mathematics and Economics,2007,40(2):322-334.

[4] C HIPP,M PLUM.Optimal investment for insurers[J].Insurance:Mathematics and Economics,2000,27(2):580-587.

[5] S DAVID PROMISLOW,V R YOUNG.Minimizing the probability of ruin when claims follow brownian motion with drift[J].North American Actuarial Journal,2005,9(3):109-128.

[6] Z LIANG,E BAYRAKTAR.Optimal reinsurance and investment with unobservable claim size and intensity[J].Insurance:Mathematics and Economics,2014,55:156-166.

[7] X LIN,Y LI.Optimal reinsurance and investment for a jump diffusion risk process under the cev model[J].North American Actuarial Journal,2011,15(3):417-431.

[8] M GU,Y YANG,S LI,et al.Constant elasticity of variance model for proportional reinsurance and investment strategies[J].Insurance:Mathematics and Economics,2010,46(3):580-587.

[9] J Z LI,R WU.Upper bounds for ruin probabilities under stochastic interest rate and optimal investment strategies[J].Acta Mathematica Sinica,English Series,2012,28(7):1 421-1 430.

[10] H ZHAO,X RONG,Y ZHAO.Optimal excess-of-loss reinsurance and investment problem for an insurer with jump-diffusion risk process under the heston model[J].Insurance:Mathematics and Economics,2013,53(3):504-514.

[11] H ZHU,C DENG,S YUE,et al.Optimal reinsurance and investment problem for an insurer with counterparty risk[J].Insurance:Mathematics and Economics,2015,61:242-254.

[12] C MUNK,C SØRENSEN,T NYGAARD VINTHER.Dynamic asset allocation under mean-reverting returns,stochastic inerest rates,and inflation uncertainty:are popular recommendations consistent with rational behavior?[J].International Review of Economics & Finance,2004,13(2):141-166.

[13] M KWAK,B H LIM.Optimal portfolio selection with life insurance under inflation risk[J].Journal of Banking & Finance,2014,46:59-71.

[14] G GUAN,Z LIANG.Optimal reinsurance and investment strategies for insurer under interest rate and inflation risks[J].Insurance:Mathematics and Economics,2014,55:105-115.

[15] 费为银,李淑娟.Knight不确定下带通胀的最优消费和投资模型研究[J].工程数学学报,2012,29(6):799-806.

[16] 杨鹏.通货膨胀影响下基于随机微分博弈的最优再保险和投资[J].应用概率统计,2016,32(2):147-156.

[17] J GRANDELL.Aspects of risk theory[M].New York:Springer-Verlag,1991.