带隔板的底水油藏水平井水脊高度计算

胡 平, 卞德智, 范子菲, 刘欣颖, 程林松

( 1. 中国石油勘探开发研究院，北京 100083； 2. 中国石化国际石油勘探开发公司，北京 100083； 3. 中国石油天然气勘探开发公司，北京 100034； 4. 中国石油大学(北京) 石油工程学院，北京 102249 )

0 引言

水平井能够有效延缓底水锥进，改变底水锥进模式，变“锥进”为“脊进”，因此被广泛用于底水油气藏的开发[1-3]。研究底水脊进规律，包括水脊高度及形态变化、水淹模式及机理，预测水平井的见水时间和临界产量等指标参数，对实现底水油藏的高效稳定开发具有重要意义。

人们采用渗流力学理论和油藏工程方法对底水脊进进行研究。Giger F M[4]建立水平井底水脊进的二维数学模型，计算临界产量和见水时间，但相关参数难以确定。Chaperon I[5]研究各向异性对水脊高度及临界产量的影响。Ozkan E等[6]刻画水平井开发底水油藏流体的流线分布。范子菲等[7]采用镜像法得出一排水平井位于底水驱动油藏顶部的临界产量公式，得到不同开发时间的临界产量。程林松等[8]采用镜像反映和势的叠加原理，得到见水时间的计算公式。范子菲和程林松等没有对水脊高度的变化规律进行研究。在水平井稳定渗流情况下,侯君等[9]给出底水油藏不同时刻和临界条件下底水脊进高度的解析解。刘振宇等[10]利用复平面坐标变换的方法，得到描述水脊位置坐标的参数方程。随着计算机技术的发展，利用数值模拟软件实现底水脊进过程的可视化，结合生产实际对水淹模式、水淹机理及影响因素进行深入研究[11-13]。隔夹层是影响底水油藏开发的重要因素，带隔板底水油藏水进规律的研究日渐成熟。李传亮等[14-15]应用第二格林公式和达西公式，分别推导出隔板和半渗透隔板底水油藏的临界产量公式。赵新智等[16]考虑隔板下部底水锥进的半球形径向流和隔板上部的平面径向流方式，应用物质平衡原理，推导低渗透带隔板底水油藏见水时间的预报公式。刘峰等[17]建立考虑启动压力梯度的低渗透带半渗透隔板的底水油藏油井见水时间预测公式。李传亮、赵新智及刘峰等考虑隔板的因素对水进规律的影响，但只针对直井井型。Yue Ping等[18]和黄全华等[19]针对带隔板底水油藏水平井的见水时间进行预测，但两者未考虑隔板的存在对渗流场的影响，并且也未给出水脊高度的计算模型及其变化规律。

在水平井开采含夹层底水油藏物理实验的基础上，笔者以多孔介质渗流理论为依据，利用镜像反映法和势的叠加原理，研究带隔板底水油藏任一时刻水脊的高度及形态，并对油井的见水时间进行预测，分析其影响因素，对油藏开发具有指导意义。

1 物理实验

为了研究带隔板底水油藏的水淹模式及水脊的变化规律，采用包括底水供给系统、三维可视化模型和记录计量系统三部分组成的物理模拟装置，对三组隔板长度不同的情况进行对比实验，呈现出相似的变化规律[20]。

含隔夹层的非均质底水油藏底水脊进典型过程见图1。实验为隔板占油藏1/2的情况，展示带隔板底水油藏水平井水脊的发展过程，可概括为“均匀托进—底水绕流—边水横扫—底水脊进—油井见水—沿井扩展—全井水淹”的水淹模式。根据实验观察，底水的水脊峰值并不是在隔板下部正中央，而是在隔板的边部；隔夹层下部在开发前期出现“屋檐油”[21]，随着生产的进行“屋檐油”的面积逐渐减小；底水绕过隔板以边水横扫的方式进行驱替的过程很短暂，迅速进入以底水脊进为主的驱替方式，水脊峰值出现在隔板以上中央的近井底处。该实验为后续水脊高度和见水时间的计算提供依据和支持。

图1 含隔夹层的非均质底水油藏底水脊进典型过程Fig.1 Representative process of water cresting in bottom water drive reservoir with barrier

2 地层中势的分布

2.1 基本假设

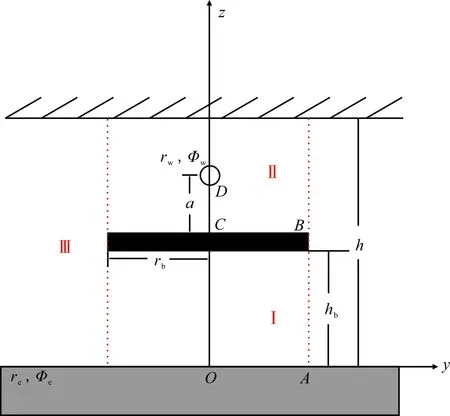
图2 带隔板底水油藏水平井示意Fig.2 Schematic diagram of horizontal wellbore in bottom water reservoir with interlayer

(1)流体在多孔介质中的流动为稳定流；

(2)油水边界为恒压或等势边界，初始势函数为Φe；

(3)忽略毛管力和相对渗透率的影响；

(4)不考虑隔板的渗透性，即隔板为不渗透隔板。

2.2 模型建立

带隔板底水油藏水平井见图2，其中rw为井筒半径；Φw为井壁处的势；a为水平井井眼中心距隔板的垂向距离；rb为隔板半径；h为油藏厚度；hb为隔板距油水界面高度；re为供给半径；Φe为供给边界处的势。当无隔板时，水质点在压差的作用下直接到达井底，沿z轴方向质点的运动速度最快，最先到达井底，离z轴水平距离越远，水质点运动速度越慢，在空间上，水体呈现脊状上升。当有隔板存在时(见图2)，在隔板宽度rb影响的范围内，水质点在压差的作用下上升，但到达隔板附近时不能继续向上穿过隔板，而是绕过隔板到达井底，即水质点运动到隔板附近时，速度在z方向上的分量值为0，隔板表现为近似分流线的性质。与无隔板的情况相比，运动方向改变，意味着有无隔板油藏中流体的势场分布不同。因此，不能按照无隔板时，油藏的势函数分布计算相关的水脊高度等参数。

为了研究油藏中势场的分布，将油藏划分为3个区分别计算势函数。以隔板为分界线，隔板下部为Ⅰ区，上部为Ⅱ区，隔板宽度影响范围以外为Ⅲ区(见图2)。Ⅰ区中流体质点向上运动的动力主要来源于底水供给边界与油井之间的压力差，并且考虑不渗透隔板对底水的阻挡，因此计算势分布时采用图3(a)的简化模型：底水为直线供给边界、隔板为封闭边界外一口水平井生产的情况。同理，Ⅱ区水脊上升的动力主要来源于油井与周围地层之间的压力差，并且在隔板的影响范围内，模型简化为顶底为封闭边界下一口水平井生产的情况，见图3(b)。Ⅲ区在隔板影响范围外，水脊上升的动力为油井与底水供给边界之间的压力差，模型简化为顶部封闭边界，底部为直线供给边界一口水平井生产的情况，见图3(c)。

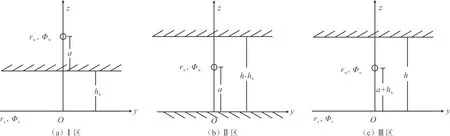
图3 带隔板底水油藏水平井物理模型分区简化模型Fig.3 Partition simplified model of horizontal well in bottom water reservoir with interlayer physical experiment

2.3 势的分布

2.3.1 Ⅰ区

根据镜像反映原理，图3(a)中的yz平面的有限区域地层，可反映无限空间两源两汇交替排列的一直线井排。在yz平面的无限空间中，直线井排上井的类别和位置可归结为四类：生产井两类，即(0,4nhb+hb+a)和(0,4nhb+hb-a)；注入井两类，即(0,4nhb-hb+a)和(0,4nhb-hb-a)，其中n=0，±1，±2，…。

设水平井长度为L，产量为Q，取q=Q/(2πL)。由势的叠加原理，得到yz平面地层中任一点势的分布为

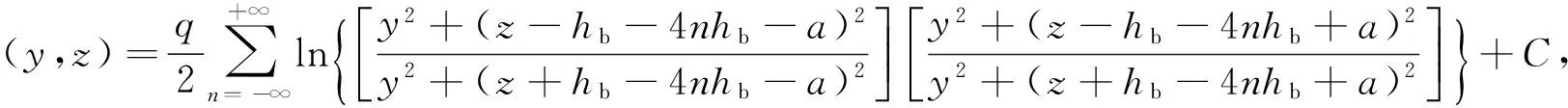
(1)

式中：Φ为势函数；C为常数。

由贝塞特公式[7]，式(1)可整理为

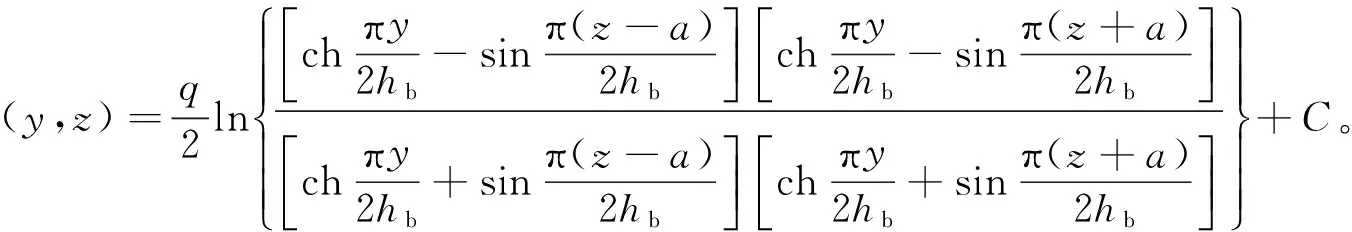
(2)

2.3.2 Ⅱ区

根据镜像反映原理，图3(b)中的yz平面的有限区域可反映无限平面中直线生产井排，生产井的井位坐标为：[0,2n(h-hb)+a]和[0,2n(h-hb)-a]，n=0，±1，±2，…,由势的叠加原理，得到yz平面上任一点势的分布为

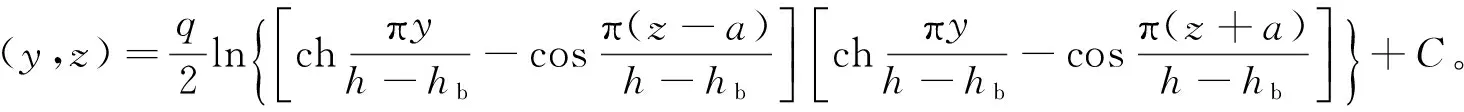
(3)

2.3.3 Ⅲ区

图3(c)中的yz平面的有限区域可反映无限空间两源两汇交替排列的直线井排，井的类别和位置可归结为四类：生产井两类，即[0,2h+4nh-(a+hb)]和[0,4nh+(a+hb)]；注入井两类，即[0,2h+4nh+(a+hb)]和[0,4nh-(a+hb)]，其中n=0，±1，±2，…。因此，yz平面上任一点势的分布[7]为

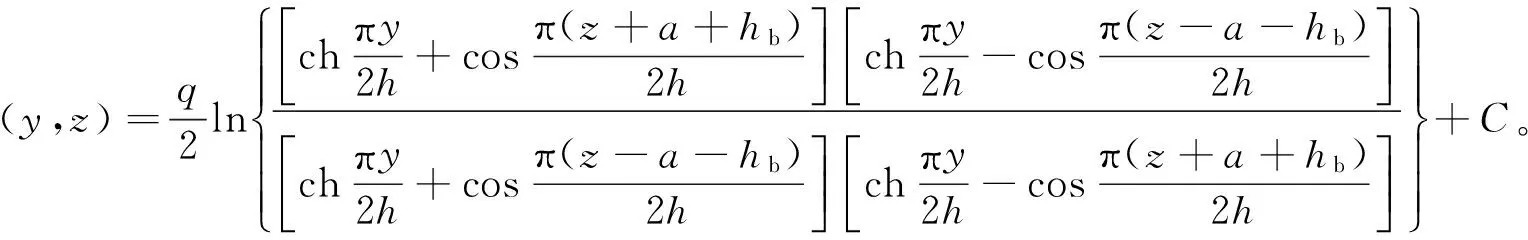
(4)

因此，为描述水脊到达井筒过程中的高度及形态，计算油井见水时间，将yz平面井筒以下区域的势函数定义为分段函数，即

3 水脊高度计算方程及见水时间

3.1 水脊高度

3.1.1 Ⅰ区

由Ⅰ区势的分布方程式(2)，求得井轴方向(y=0，即隔板正下方)上势函数梯度为

(5)

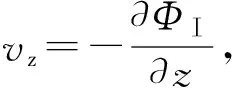
(6)

式中：vz为流体的渗流速度v在z方向上的分量。渗流速度与流体质点的平均真实速度u的关系为

(7)

式中：φ为孔隙度；t为流体质点运动时间。对式(7)进行分离变量积分，将式(6)代入，有

(8)

积分得在井轴上(y=0)不同时刻水脊高度的计算式，即

(9)

另外，由式(2)可得

(10)

(11)

3.1.2 Ⅱ区

同样，根据Ⅱ区势的分布方程式(3)，可得井轴方向(y=0)上势函数梯度，即

(12)

沿井轴方向上水脊高度的计算式为

(13)

沿y方向的势梯度为

(14)

由式(14)，得Ⅱ区水脊面距离侧向距离y随时间t的变化为

(15)

3.1.3 Ⅲ区

由式(4),对y=rb的隔板边缘求得z方向的势梯度为

(16)

可得y=rb处不同时刻水脊高度为

(17)

其中，

同样，由y方向的势梯度，可得Ⅲ区的水脊离井轴侧向距离y随时间的变化，即

(18)

由于水脊形状关于z轴对称，y=-rb处水脊高度的变化及[-rb,y]范围内的水脊侧向距离的计算同式(17)及式(18)。综合式(9)、式(11)、式(13)、式(15)、式(17)和式(18)，利用MATLAB软件编制计算程序，计算不同时刻的水脊高度及其与井轴的侧向距离，得到一系列离散的数值解；而后将数据点勾画起来，即可对某一时刻水脊形状进行描述。

3.2 见水时间

底水在Ⅰ区向上运动，在绕过隔板到达Ⅱ区之前，水脊的峰值出现在隔板边缘y=±rb处，绕过隔板进入Ⅱ区，先以边水的方式驱替，再以底水脊进的方式驱替，水脊的峰值出现在隔板中央正上方的井轴y=0处。在计算见水时间时，假设水质点的运动路线(见图3)为：水质点由A点运动到B点，再沿着隔板由B点运动到C点，最后到达井筒D。见水时间为

t=tAB+tBC+tCD。

(19)

令式(17)中z=hb，得到tAB；由式(15)中z=hb，y=rb得到tBC；在式(13)中，令z=hb+a-rw，即可得到tCD。

4 实例分析

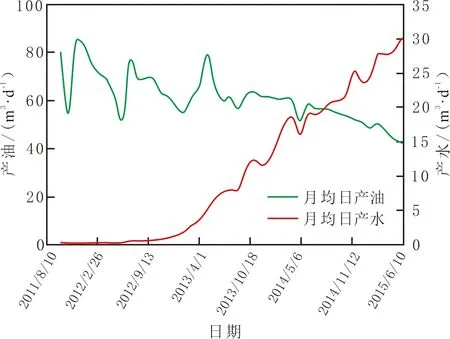
图4 某油井月均产量随时间变化曲线Fig.4 The average daily production changes with time for a certain well

以南美某一带隔夹层的底水油藏水平井为例，其基本参数：油藏压力为14.9 MPa，温度为87.7 ℃，地层原油黏度为4.02 mPa·s，原油体积因数为1.042，油藏厚度h=20.7 m，隔板到油水界面距离hb=12 m，水平井到隔板距离a=2 m，油藏孔隙度φ=0.33，水平井筒长度为198 m，井径rw=0.088 m，隔板半径rb=20 m，油井初期产油量约为80 m3/d。油井的产量变化曲线见图4。由图4可知，油井的见水时间为585 d，根据式(19)，由MATLAB编制的计算程序，得到tAB=470 d，tBC=141 d，tCD=3 d，即t=614 d，与实际情况相比，误差约为4.9%，其计算结果相对合理。

4.1 水脊形态变化特征

各分区距离原点不同位置处的水脊高度z随时间的变化见图5-7。由图5-7可知：对于Ⅰ区，水脊高度随时间的增加而增加，但增加速度逐渐减慢，当时间达到2×103d时，水脊高度变化很小，甚至趋于定值，即水脊高度难以达到隔板高度处，两者之间的高度差范围内，底水很难波及而形成所谓的“屋檐油”；距离原点(隔板中间正下方)越近的位置水脊高度越低，越远的位置(隔板边缘附近下方)水脊高度越高，表明越靠近隔板正下方中央位置，隔板对底水脊进的抑制作用越强，而在隔板边缘附近抑制作用减弱；在某一时刻，当y均匀增加时，水脊高度z并不均匀增加，近原点位置处z的差异较小，远离原点位置处z的差异变大，表明隔板对底水的抑制作用沿y轴方向并不是均匀减弱。当底水绕过隔板到达Ⅱ区后，水脊高度随时间的增加呈线性变化，表明底水能量充足，导致水线在隔板上方均匀推进；y越小，直线的斜率越大，表明越靠近水平井处压差越大，水脊高度上升越快；在同一时刻，y越小，越靠近水平井井底，水脊高度沿y方向的差异越大，即水脊高度z在近水平井正下方、隔板正上方位置处变化大，随y取值均匀增加，z的差异减小。对于Ⅲ区，水脊高度随时间的增加而增加，增加的速度逐渐减慢；离隔板边缘正下方处越远，水脊高度越低，水脊高度差沿y方向的变化越小，即水脊趋于平缓。根据计算的数值结果，作出3个时间节点的水脊形状(见图8)，隔板下方“屋檐油”的存在，为底水油藏水平井生产的进一步挖潜指明方向。计算得到的水脊形态变化特征与物理实验结果可以相互验证。

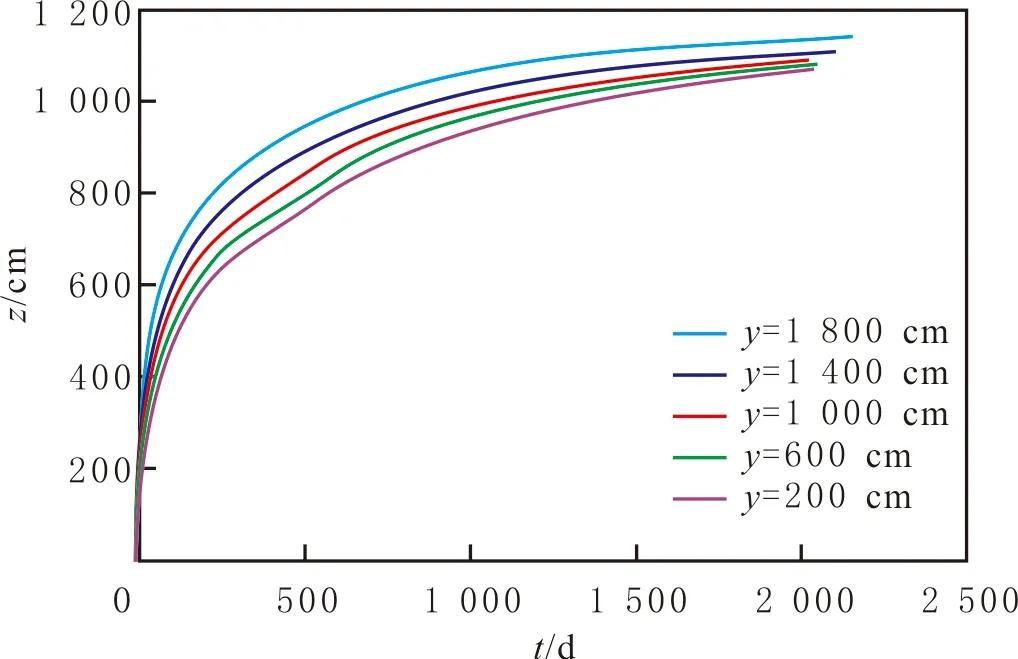
图5 Ⅰ区水脊高度随时间变化Fig.5 Water cresting height changes with time for zone Ⅰ

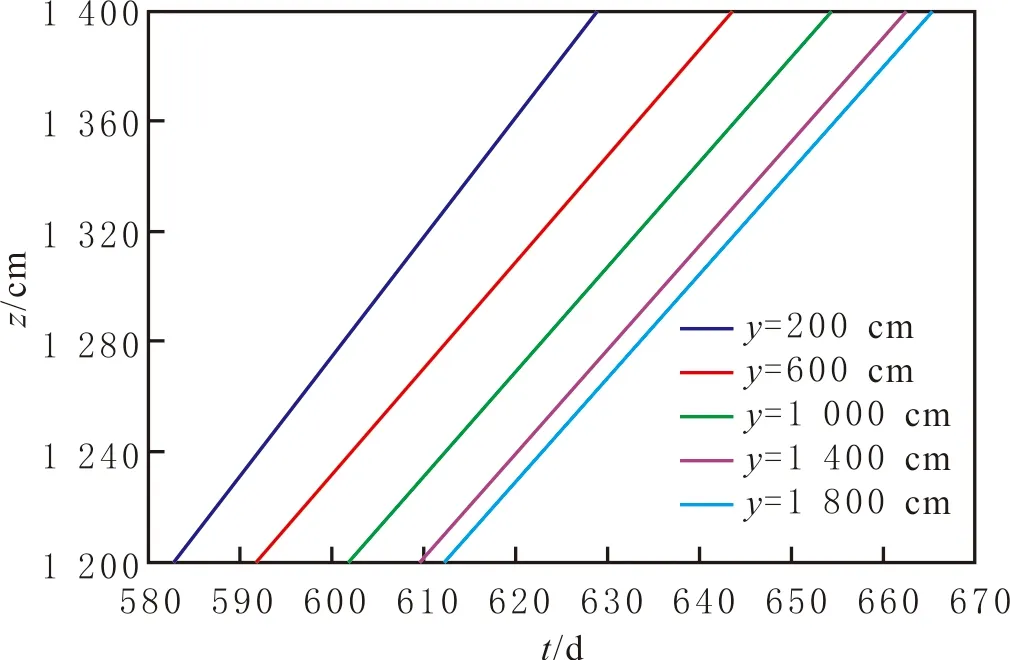
图6 Ⅱ区水脊高度随时间变化Fig.6 Water cresting height changes with time for zone Ⅱ

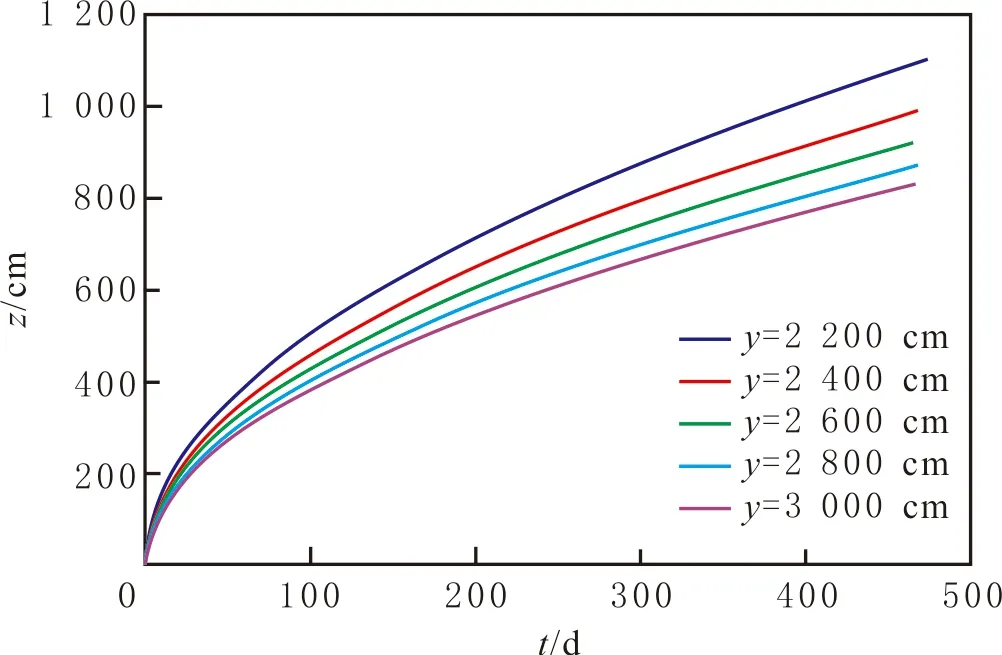
图7 Ⅲ区水脊高度随时间变化

Fig.7 Water cresting height changes with time for zone Ⅲ

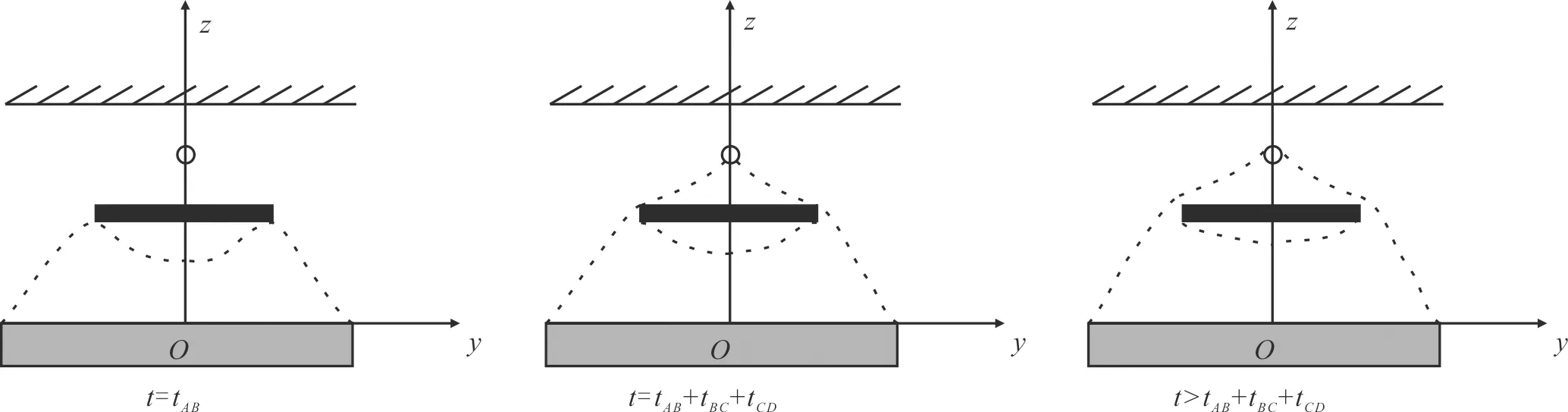
图8 不同时间节点水脊形态Fig.8 The water cresting shape under different time

4.2 见水时间影响因素

研究不同因素，包括隔板半径、隔板距水平井的垂直距离，以及油井产量对带隔板底水油藏水平井见水时间的影响(见图9)。由图9可知，水平井见水时间随隔板半径的增大而相应延后，即水平井见水越晚。以隔板半径20 m为拐点，当隔板半径低于20 m时，见水时间随隔板半径的增大变化幅度较小，当隔板半径大于20 m时，见水时间随隔板半径的增大变化幅度变大，明显改善油井的生产效果。隔板与水平井间的垂直距离对见水时间的影响表现出类似的变化规律(见图10)：隔板距离水平井的垂直距离越大(隔板距离底水越近)，隔板对底水的抑制作用越强，油井见水越晚。当隔板与井的垂直距离在5 m以上时，见水时间变化明显。见水时间随油井产量的增加而减小，即水平井见水时间提前。当油井产量小于50 m3/d时，见水时间随油井产油量的增加明显提前，油井产量大于50 m3/d后，见水时间变化幅度逐渐减小(见图11)。因此，在实际生产中控制油井的产油量，在保证产能的基础上可以延缓见水时间。

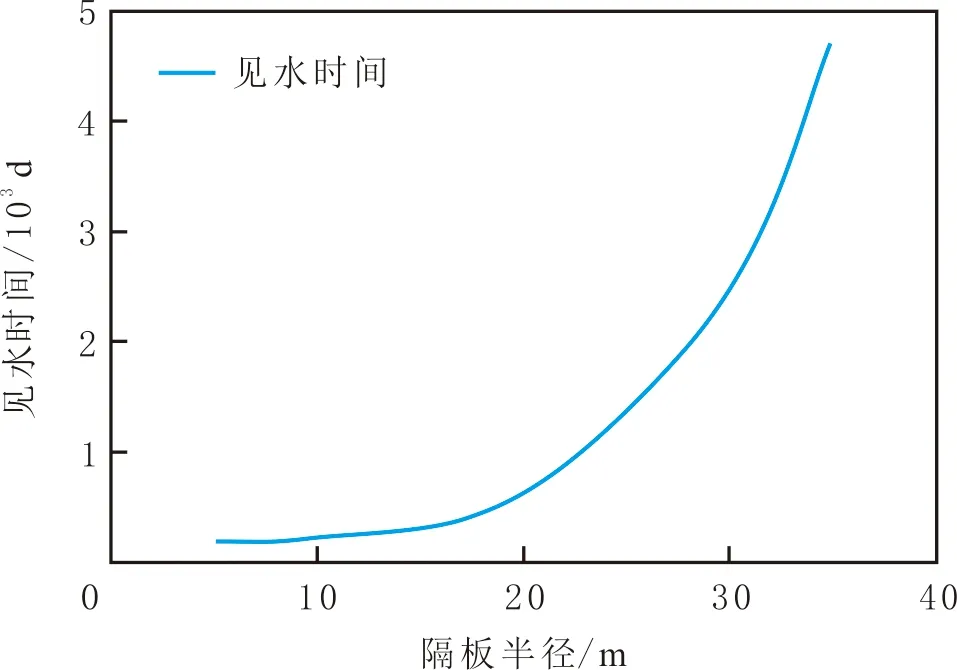
图9 隔板半径对见水时间的影响Fig.9 The effect of interlayer radius on water breakthrough time

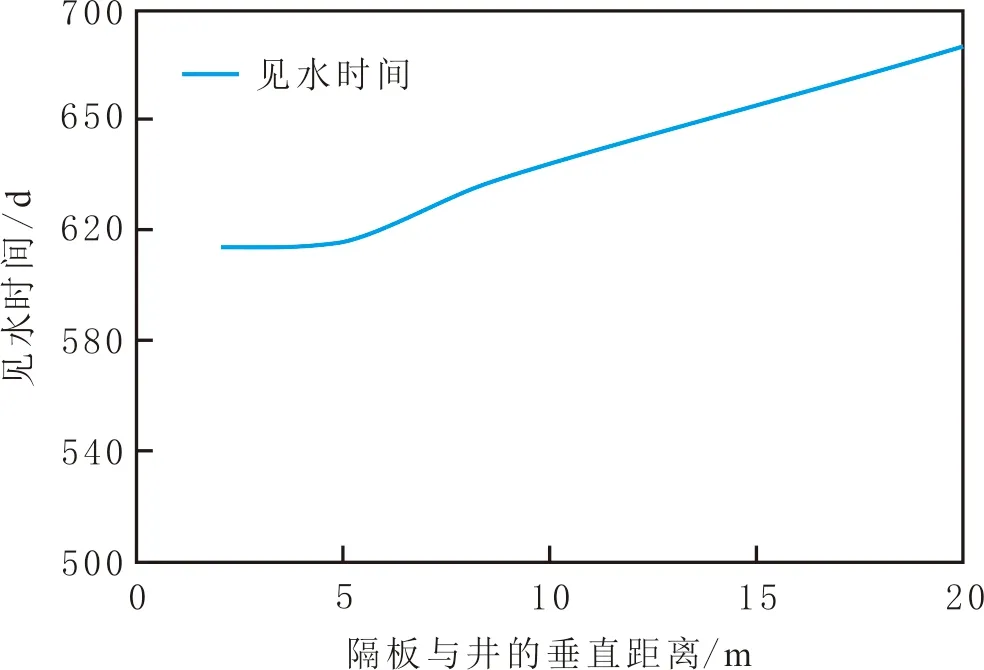
图10 隔板与井的垂直距离对见水时间的影响Fig.10 The effect of vertical distance away from well on water breakthrough

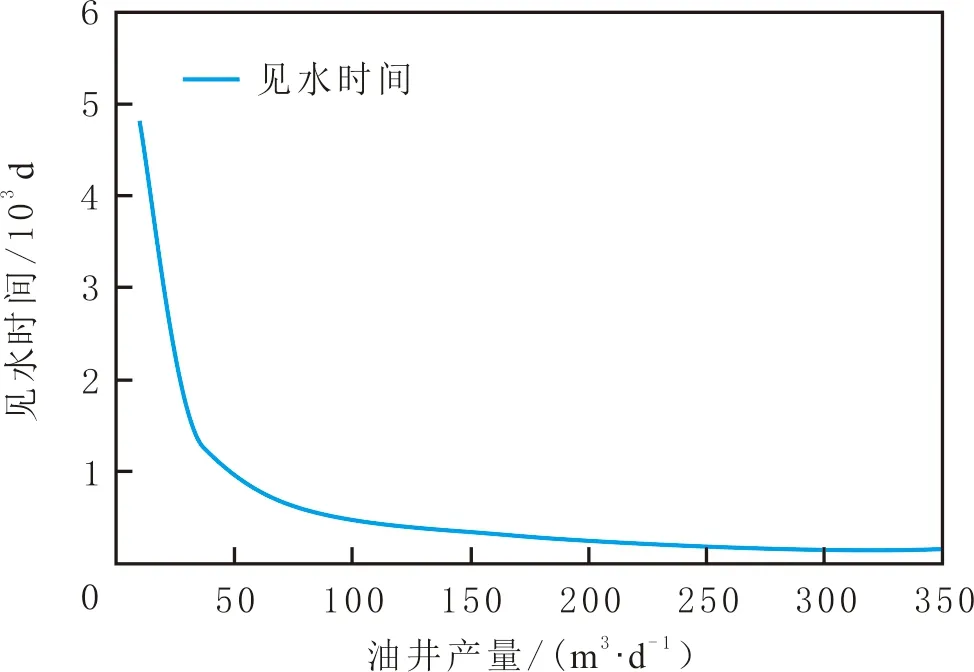
图11 油井产量对见水时间的影响

5 结论

(1)不同分区内，水脊高度随时间的变化规律不同。在Ⅰ分区内，水脊高度随时间的增加而增加，但增加速度逐渐减慢，甚至趋于定值，水脊高度与隔板所在位置的高度差范围内形成“屋檐油”；在某一时刻，水脊高度z在近原点位置处沿y方向差异较小，远离原点位置处z的差异变大。在Ⅱ分区内，水脊高度随时间的增加呈线性变化；在同一时刻，越靠近水平井井底，水脊高度沿y方向的差异越大。在Ⅲ分区内，水脊高度随时间的增加而增加，增加的速度逐渐减慢；离隔板边缘正下方处越远，水脊高度越低，水脊高度差沿y方向的变化越小。

(2)水平井见水时间随隔板半径的增大而相应延后，当隔板半径大于20 m时，见水时间随隔板半径的增加变化幅度增大；隔板距离水平井的垂直距离越大，油井见水越晚，当隔板与井的垂直距离在5 m以上时，见水时间明显延缓；见水时间随油井产量的增加而缩短，油井产量大于50 m3/d后，见水时间变化幅度逐渐减小；见水时间与实际误差约为4.9%。

[1] 黄小荷,朱维耀,岳明,等.基于分形几何的裂缝型底水气藏产能模型[J].东北石油大学学报,2013,37(6):86-93.

Huang Xiaohe, Zhu Weiyao, Yue Ming, et al. Productivity model of fractured bottom-water gas reservoir based on fractal geometry [J]. Journal of Northeast Petroleum University, 2013,37(6):86-93.

[2] 王春智,李兆敏,李松岩,等.水平井开发底水稠油油藏氮气泡沫和冻胶控水三维物理模拟试验[J].中国石油大学学报:自然科学版,2015,39(6):118-123.

Wang Chunzhi, Li Zhaomin, Li Songyan, et al. Experimental study on water control and oil recovery in bottom water driving reservoirs using plugging agents [J]. Journal of China University of Petroleum: Edition of Natural Science, 2015,39(6):118-123.

[3] 刘欣颖,胡平.非均质底水油藏水平井三维物理模拟实验[J].石油学报,2011,32(6):1012-1016.

Liu Xinying, Hu Ping. A 3-D visible physical experiment on horizontal wells of heterogeneous reservoirs with bottom water [J]. Acta Petrolei Sinica, 2011,32(6):1012-1016.

[4] Giger F M. Analytic 2-D models of water cresting before breakthrough for horizontal wells [R]. SPE 15378, 1989.

[5] Chaperon I. Theoretical study of coning toward horizontal and vertical wells in anisotropic formations: Subcritical and critical rates [R]. SPE 15377, 1986.

[6] Ozkan E, Raghavan R. Performance of horizontal wells subject to bottomwater drive [R]. SPE 18559, 1990.

[7] 范子菲,林志芳.底水驱动油藏水平井临界产量公式及其变化规律研究[J].石油勘探与开发,1994,21(1):65-70.

Fan Zifei, Lin Zhifang. A study of critical rate of a horizontal well in a reservoir with bottom-water drive [J]. Petroleum Exploration and Development, 1994,21(1):65-70.

[8] 程林松,郎兆新,张丽华.底水驱油藏水平井锥进的油藏工程研究[J].石油大学学报:自然科学版,1994,18(4):43-47.

Cheng Linsong, Lang Zhaoxin, Zhang Lihua. Reservoir engineering problem of horizontal wells coning in bottom-water driven reservoir [J]. Journal of University of Petroleum: Edition of Natural Science, 1994,18(4):43-47.

[9] 侯君,程林松,李春兰.底水油藏水平井水脊高度的计算[J].水动力学研究与进展,2006,21(3):374-380.

Hou Jun, Cheng Linsong, Li Chunlan. Calculaiton of water cresting height for horizontal well in bottom-water [J]. Journal of Hydrodynamics, 2006,21(3):374-380.

[10] 刘振宇,程博,刘洋,等.水平井开发研究-底水油藏的水脊变化及见水时间预测[J].大庆石油学院学报,2002,26(4):100-103.

Liu Zhenyu, Cheng Bo, Liu Yang, et al. Water cresting characteristics and determination of breakthrough time for horizontal wells [J]. Journal of Daqing Petroleum Institute, 2002,26(4):100-103.

[11] 周代余,江同文,冯积累,等.底水油藏水平井水淹动态和水淹模式研究[J].石油学报,2004,25(6):73-77.

Zhou Daiyu, Jiang Tongwen, Feng Jilei, et al. Waterflooding performance and pattern in horizontal well with bottom water reservoir [J]. Acta Petrolei Sinica, 2004,25(6):73-77.

[12] 姜汉桥,李俊键,李杰.底水油藏水平井水淹规律数值模拟研究[J].西南石油大学学报:自然科学版,2009,31(6):172-176.

Jiang Hanqiao, Li Junjian, Li Jie. Investigation on water-out mechanism of bottom water driven reservoir in horizontal wells [J]. Journal of Southwest Petroleum University: Science and Technology Edition, 2009,31(6):172-176.

[13] 王敬,刘慧卿,刘松原,等.非均质底水油藏水平井水淹规律研究[J].石油学报,2010,31(6):970-974.

Wang Jing, Liu Huiqing, Liu Songyuan, et al. A flooding law in horizontal wells of heterogeneous reservoirs with bottom water [J]. Acta Petrolei Sinica, 2010,31(6):970-974.

[14] 李传亮,宋洪才,秦宏伟.带隔板底水油藏油井临界产量计算公式[J].大庆石油地质与开发,1993,12(4):43-46.

Li Chuanliang, Song Hongcai, Qin Hongwei. Computation formula of critical production oil wells in reservoir with bottom water and confining bed [J]. Petroleum Geology and Oilfield Development in Daqing, 1993,12(4):43-46.

[15] 李传亮.半渗透隔板底水油藏油井见水时间预报公式[J].大庆石油地质与开发,2001,20(4):32-33.

Li Chuanliang. Prediction formula for water breakthrough time of semipermeable partition bottom water reservoir [J]. Petroleum Geology and Oilfield Development in Daqing, 2001,20(4):32-33.

[16] 赵新智,朱圣举.低渗透带隔板底水油藏油井见水时间预测[J].石油勘探与开发,2012,39(4):471-474.

Zhao Xinzhi, Zhu Shengjyu. Prediction of water breakthrough time for oil wells in low-permeability bottom water reservoirs with barrier [J]. Petroleum Exploration and Development, 2012,39(4):471-474.

[17] 刘峰,洪建伟,任建红,等.低渗透带半渗透隔板的底水油藏油井见水时间预测[J].钻采工艺,2014,37(2):51-53.

Liu Feng, Hong Jianwei, Ren Jianhong, et al. Study on water breakthrough time prediction for oil wells in low-permeability bottom water reservoirs with semi-permeable barrier [J]. Drilling & Production Technology, 2014,37(2):51-53.

[18] Yue Ping, Du Zhimin, Chen Xiaofan, et al. The critical rate of horizontal wells in bottom-water reservoirs with an impermeable barrier [J]. Petroleum Science, 2012,9(2):223-228.

[19] 黄全华,陆云,付云辉,等.带隔板底水油藏水平井见水时间预测方法[J].油气地质与采收率,2016,23(6):82-86.

Huang Quanhua, Lu Yun, Fu Yunhui, et al. Prediction method of water breakthrough time of horizontal wells in bottom water reservoir with barrier [J]. Petroleum Geology and Recovery Efficiency, 2016,23(6):82-86.

[20] 刘欣颖,胡平.水平井开采含夹层底水油藏三维物理模拟试验研究[J].石油天然气学报,2011,33(8):129-133.

Liu xinying, Hu Ping. 3-D Physical experiment on horizontal well production in bottom water reservoirs with interbeds [J]. Journal of Oil and Gas Technology, 2011,33(8):129-133.

[21] 薛永超,粱卫,耿传林.夹层对底水油藏油水运动的控制作用[J].西安石油大学学报:自然科学版,2011,26(1):14-17.

Xue Yongchao, Liang Wei, Geng Chuanlin. Control effect of inter-layers on the migration of oil and water in bottom-water reservoirs [J]. Journal of Xi'an Shiyou University: Natural Science Edition, 2011,26(1):14-17.