SWIM水文模型在王家坝地区的适用性评估
2018-03-29姚梦婷孙艳伟
高 超, 陆 苗, 姚梦婷, 孙艳伟
(1.宁波大学 地理与空间信息技术系, 浙江 宁波 315211; 2.安徽师范大学 国土资源与旅游学院, 安徽 芜湖 241000)
在气候急剧变化的背景下,水文序列的稳定性遭到了破坏,使得极端水文事件频发[1-2]。利用水文模型可为探索水文过程在气候变化下的响应关系与极端水文事件发生规律提供科学依据和实现平台[3-6]。然而,水文模型结构较为复杂,模型的各个参数具有时空变异性,尤其是具有物理基础的分布式水文模型,其参数与下垫面条件有着密切的联系。因此,评估模型参数取值变化对模拟精度的影响,可为水文模型的高效优化和率定工作提供基础支撑[7-8]。
分布式水文模型是一种较为真实科学模拟水文过程的有效途径[9],HBV(hydrologiska fyrans vattenbalans modell)[10-11]、SWAT(soil and water assessment tool)[12-13]、新安江模型[14]等模型在中国应用较广。SWIM(soil and water integrated model)模型由德国波茨坦研究所在SWAT和MATSALU模型基础上开发,该模型整合了流域尺度内的水文、植被、侵蚀和养分输送等各个方面,具有良好的物理基础,且相较于SWAT,SWIM模型能实现日尺度的模拟,对流域进行空间上划分为多个子流域,结合适当的水资源管理数据等,以及适中的数据需求都是该模型的重要优点[15]。有学者研究得出SWIM模型的模拟在中国淮河流域、黑龙江流域等均具有较好的适应性,适合气候变化背景下的水文过程研究[16]。然而,SWIM模型在中国尚未得到广泛应用,目前国内对于SWIM模型的研究仍然有限,主要集中在研究模型的尺度效应问题[17],探讨模型在不同区域的适用性,利用模型研究下垫面对水文过程的影响,水文要素对气候变化的响应等[18-19],但对模型参数的率定大多基于经验进行,率定过程的科学性有所欠缺。有学者比较了SWIM模型中7个可率定参数与模型的敏感性[18],但是缺少分析这7个参数的取值变化对模型精度的影响。因此,本研究通过人工扰动分析法对重点参数确定调整范围并手动赋值,分析并检验特定参数变化对模型输出结果的影响。
综上,本研究拟以淮河流域王家坝地区为研究区,利用王家坝地区率定期(1959—1978年)和验证期(1979—2008年)的实测数据,自动率定SWIM水文模型,得到最优的参数组合,并对率定好的SWIM模型的模拟精度进行评价,讨论SWIM模型在王家坝地区的适用性,为王家坝地区洪涝灾害的预报和减灾提供科学支持,旨在为SWIM模型参数率定工作提供参照,推进SWIM模型率定工作的科学化。
1 研究区概况
本研究区是利用SWIM水文模型,以中国淮河流域上游地区王家坝闸(115°47′E,32°19′N)为出口断面,基于数字高程图(DEM)划分得到的王家坝闸的集水区,研究区范围为淮河流域以内、自王家坝闸以上至桐柏地区的区域,总面积约2 050 500 hm2,地处淮河流域中游和上游之间,在蒙洼蓄洪区的上游,王家坝闸水文站的地理坐标位置为东经115°47′,北纬32°19′。研究区地势整体上呈西高东低的态势,地貌类型丰富,海拔高度最高可达869 m。研究区内属半湿润季风气候,降水年际变化大,多年平均年降水量为1 018 mm。据资料记载,王家坝地区分别在1954,1964,2003年以及2007年发生了大洪水。
2 数据来源
实测气象数据包括研究区内8个气象站点(桐柏、平玉、新蔡、正阳、息县、信阳、罗山、潢川)的1959年1月1日至2008年12月31日实测气象数据,由中国气象局国家气候中心提供。包括最高温、最低温、平均温、降水、湿度、日照时数、日辐射量等。
径流数据主要是指王家坝闸1959年1月1日至2008年12月31日的实测径流数据,由淮河水利委员会提供。涉及到的地理数据主要包括研究区内DEM数据,土地利用数据和土壤数据。DEM数据为90 m空间分辨率的SRTM数据,来自中国科学院的地理空间数据云网站(http:∥www.gscloud.cn)。土壤数据空间分辨率为800 m,由联合国粮农组织(FAO)全球土壤数据库(http:∥www.fao.org/)提供。土地利用数据为1∶100 000,由中国科学院资源环境科学数据中心提供。所有地理数据在输入SWIM水文模型之间,均需要对像元大小进行重采样至400 m×400 m。
3 模型参数与率定
3.1 自动率定
本研究中SWIM模型采用自动率定方法,分别对模型的7个可调节参数进行率定。考虑到模型存在预热期,自动率定以除第一年以外计算出的纳西效率系数为判定标准。基本思想为:从第一个可调节参数开始,在其取值范围内以一定的步长取数,运行模型并计算纳西效率系数,取最优值并记录,再以同样的方法调节所有参数并记录下他们的最优值,此为一个循环。考虑到不同参数组合会有不同效果,自动率定过程一般进行多个循环,直到纳西效率系数不再提高时,得到最优结果。
3.2 参数的物理意义及范围
SWIM模型水文过程的模拟总体上涉及到10个过程,分别是融雪计算过程、地表径流计算过程、径流峰值计算过程、下渗量计算过程、侧向壤中流计算过程、潜在蒸散计算过程、土壤蒸发和植物蒸腾计算过程、地下径流计算过程、传输损耗的计算过程以及最终的径流汇流过程。其中,对模拟结果影响最大的主要是地表径流计算过程、潜在蒸散计算过程以及径流汇流过程,其参数具有明确的物理意义,其中可调节的主要包括以下7个参数[15]。
(1) thc。SWIM模型基于Priestley-Taylor公式计算潜在蒸散,thc是模型在潜在蒸散计算模块中,对大气散射率的校正因子。该参数取值范围为0~1,为0时代表不考虑大气散射率因子,为1时代表考虑大气散射率因子。
(2) bff。基流因子,用于计算回流的行进时间,取值范围为0~1。回流时间可被用于计算土壤层的渗透量。其取值与流域的特性有关,不同特性河流的基流因子取值参考值如表1所示。

表1 不同河流基流因子参考值
(3) cnum1,cnum3。SWIM模型基于SCN-CN模型(即径流曲线数法)计算地表径流,cnum1和cnum3分别为径流曲线数法中条件1和条件3下的CN值,仅当参数icn为1时,cnum1和cnum3才可作为率定参数。其取值范围为1~100,且cnum1 (4) gwq0。gwq0是初始地下流对径流量的贡献,单位为mm/d,取值范围为0.01~1。 (5) abf0。abf0为地下水阿尔法因子,与地下水回流到地表径流的速率有关,用于反映地下水的衰退特征,其取值范围是0.01~1。 (6) roc2,roc4。roc2,roc4是河道的汇流系数,受河道的长度和流速影响。其取值范围为1~100,且roc2 (7) sccor。为饱和传导率校正因子,其取值范围为0.01~10。 模型采用Nash-Sutcliffe效率系数 和相对误差 作为目标函数对模型进行率定。Nash-Sutcliffe效率系数 的计算公式如下[18]: (1) (2) R的取值范围是0~100%,R越小,表示模拟误差越小,模拟精度越高。 SWIM模型的7个参数通过步长加速法进行率定,并利用纳西效率来判断最优参数组合,结果如表2所示。 表2 参数率定过程及结果 3.5.1 日序列模拟总体精度评价 利用最优参数组合率定后的SWIM模型对率定期(1959—1978年)及验证期(1979—2008年)日径流量序列模拟的结果如图1所示,纳西效率分别达到0.79及0.81,相对误差R分别为22%及7.8%,总体上率定期及验证期SWIM模型模拟的径流量与实测径流量相关性较好。模拟的日径流量序列总体略高于实测日径流量序列,特别是在低值区和极端高值区。这主要是由于SWIM模型模拟的逐日径流量序列是天然的径流量序列,而实测的径流量则是受到一系列人类活动影响之后所测得的径流量。例如水利工程的修建,生活用水、工业用水以及农业用水对径流的损耗等。 图1 率定期(1959-1978年)与验证期(1979-2008年)日径流量序列模拟结果 3.5.2 日序列逐年模拟精度评价 率定期(1959—1978年)模拟径流量日序列逐年纳西效率如图2(a)所示。20 a中,有13 a的纳西效率在0.6以上,1961和1966年纳西效率较低。率定期SWIM模型在1961,1966和1978年的模拟精度很低,这与SWIM水文模型对于径流量低值模拟效果较差有一定关系。据历史资料记载,淮河流域1966和1978年发生一级大旱,1961年发生3级大旱。此外,1968年8月淮河流域发生特大洪水,由于SWIM模型在汛期模拟效果较好,致使1968年的模拟精度较好,进一步证实了SWIM模型对于径流量高值模拟效果较好,对于径流量低值模拟效果较差。 验证期(1979—2008年)模拟径流量日序列逐年纳西效率如图2(b)所示。30 a中,有25 a的纳西效率在0.6以上,1992,1993年以及1999年纳西效率较低。率定期SWIM模型在1999年的模拟精度最低。1999年,淮河流域发生严重旱灾,出现了自1979年以后的首次断流,王家坝水文站8月多日径流量为0。SWIM水文模型对于径流量低值模拟效果较差,故1999年模拟精度很低。 图2 率定期(1959-1978年)与验证期(1979-2008年)模拟径流量日序列逐年纳西效率 3.5.3 SWIM模型适用性评估 综合SWIM模型在率定期和验证期对王家坝地区日径流量序列的模拟精度,可以看出SWIM模型总体上对王家坝地区适用性较好,仅在少数干旱年份如1961,1966,1978和1999年模拟效果较差。SWIM模型可以用于王家坝地区的径流量模拟,尤其适合研究王家坝地区的洪水预报工作。 针对SWIM模型中可率定的7个参数,选取1979—2008年时间段,通过人工扰动分析法对重点参数确定调整范围并手动赋值,分析并检验特定参数变化对模型精度的影响。 为探讨日径流量序列对thc取值变化的敏感性,选取王家坝地区典型洪灾年份2003年进行讨论。王家坝水文站2003年逐日径流量序列随thc取值的变化曲线如图3所示。 由图3可知,王家坝站2003年日径流量序列的模拟结果对thc取值的变化较敏感,且汛期相对于非汛期而言,更加敏感。根据前文结论,SWIM模型在汛期模拟精度较高,非汛期模拟精度较低。由此可以进一步验证模拟精度差的时间段对于thc取值的变化更为敏感。 图3 2003年日径流量序列对thc取值变化的敏感性 选取对thc取值的变化较敏感的月份8—12月,进一步研究thc取值变化对径流量序列的影响。由图4看出,随着thc取值逐渐增大,模拟的日径流量序列值逐渐增大。在非汛期SWIM模型的模拟值偏高,因此,随着thc取值的增大,SWIM模型的模拟径流量值会进一步增大,模拟精度会进一步降低。 图4 2003年8-12月日径流量序列对thc取值变化的敏感性 对于纳西效率系数和相对误差等指标整体而言,随着thc值的增大,各年份纳西效率系数显著下降。尤其是纳西效率系数低的年份,对于thc取值的变化更为敏感,其中1999年的纳西效率对thc的变化最敏感,其次是1992年。随着thc值的增大,各年份相对误差显著下降。尤其是相对误差高的年份,对于thc取值的变化更为敏感,且整体上相对误差对thc取值的敏感性比纳西效率系数更强。 选取2003年日径流量序列,讨论研究日径流量序列对bff取值变化的敏感性。由图5可知,王家坝站2003年日径流量序列的模拟结果对bff取值的变化较敏感。随着bff值的增大,径流曲线的波动幅度变大,即模拟径流量序列在峰值区值变大,在低值区值变小。由于模拟值总体高于实测值,年内高值区模拟值增高导致模拟精度进一步下降,低值区模拟值减小,导致模拟精度上升。二者的叠加作用,导致各年份纳西效率总体无显著变化。 图5 2003年日径流量序列对bff取值变化的敏感性 对于纳西效率系数和相对误差等指标整体而言,各年份纳西效率系数与相对误差对bff的变化不敏感,随着bff值的升高,各年份纳西效率系数与相对误差基本没有变化,仅在1979年,纳西效率与相对误差有细微的变化。因此,总体上认为率定期纳西效率与相对误差对bff取值变化不太敏感。 cnum1,cnum3的取值范围为1~100,cnum2模型默认值为55,且cnum1 表3 1979-2008年纳西效率对cnum1,cnum3取值变化的敏感性 1979—2008年逐年纳西效率和逐年相对误差对gwq0取值变化的敏感性分别如图6所示,各年份纳西效率和相对误差对gwq0的变化不敏感,随着gwq0值的增大,逐年纳西效率和相对误差除1979年外,基本无变化。1979年是率定期第1 a,受模型预热影响,因此,认为模型逐年模拟精度对gwq0变化不敏感。 1979—2008年逐年纳西效率与相对误差对abf0取值变化的敏感性如图7所示。由图7可以看出,各年份纳西效率与相对误差对abf0的取值变化不敏感,基本可以忽略不计。 图6 1979-2008年逐年纳西效率及相对误差对gwq0取值变化的敏感性 图7 1979-2008年逐年纳西效率及相对误差对abf0取值变化的敏感性 王家坝地区2003年日径流量序列对roc2和roc4取值变化的敏感性分别如图8—9所示,可见日径流量序列对roc2和roc4取值的变化均较为敏感,其中:对roc4取值的变化更为敏感。对于roc2取值的变化,汛期大于非汛期。随着roc4取值的增大,径流曲线的波动幅度变小,径流曲线越来越趋向平滑。 图8 2003年日径流量序列对roc2取值变化的敏感性 图9 2003年日径流量序列对roc4取值变化的敏感性 王家坝水文站2003年逐日径流量序列随sccor取值的变化曲线如图10所示,王家坝站2003年日径流量序列的模拟结果对sccor取值的变化较敏感。随着sccor取值的增大,径流曲线的波动幅度变小,汛期模拟精度提高,非汛期模拟精度降低。 图10 2003年日径流量序列对sccor取值变化的敏感性 (1) 评估SWIM模型在王家坝地区适用性:结果表明,率定后的SWIM模型在王家坝地区适用性良好,率定期模拟日径流量序列纳西效率达到0.79,相对误差为22%,验证期模拟日径流量序列纳西效率达到0.81,相对误差为7.8%。 (2) SWIM模型在王家坝地区参数敏感性分析:根据参数的物理意义和取值范围,分析SWIM在王家坝地区对主要7个可率定参数的敏感性。结果表明,SWIM模型模拟结果在王家坝地区对thc,cnum1,cnum3,roc2,roc4,sccor取值变化较敏感,对参数bff,gwq(),abf()取值变化不敏感。其中:随着参数thc值的增大,各年份的相对误差显著下降,且整体上相对误差对thc取值的敏感性比纳西系数更强;相比较roc2,roc4取值的变化更能影响日径流序列,而对于roc2取值的变化,汛期大于非汛期;随着参数sccor取值的增大,汛期模拟精度提高,非汛期模拟精度降低。 本研究引入了具有物理基础的分布式水文模型SWIM模型,评价了其在王家坝地区的适用性,分析了其参数敏感性,从而得出结论。与常用的水文模型相比,SWIM模型调参过程中更加重视地下水水文过程。HBV(hydrologiska fyrans vattenbalans)模型在水文模拟过程中可以进行优选的参数有12个,分为积融雪模块、土壤模块、响应模块与路径模块。其中:涉及地下水水文过程的参数较少,仅有基流出流系数来调节基流的退水系数,控制基流的多少[19]。淮河流域地表水与浅层地下水会发生直接的水力联系,地下水对地表水的补给是水文过程中重要的一部分。在SWIM模型中,地下水水文过程中可调节的参数有基流因子(计算回流的行进时间)、初始地下流对径流量的贡献、地下水阿尔法因子(反映地下水的衰退特征),可以通过调节这些参数,更好地模拟地下水水文过程。在淮河流域水文模型参数率定方面,SWAT(soil and water assessment tool)模型中与水文过程相关的参数包括土壤参数、土地利用参数、地下水径流参数、融雪径流参数、地表特征参数[20]。有研究得出SWAT模型在淮河上游地区,有效水容量AWC,SCS径流曲线数CNZ,土壤蒸发补偿系数ESCO为主要敏感性参数[21],这与本研究结果中关于淮河流域上游SWIM模型的敏感参数类型较为一致。目前SWIM模型在国内尚未得到广泛应用,关于其参数敏感性方面的研究也较少涉及,在后续研究中可对模型的区域适用性及参数敏感性进行研究,以期提高水文模型模拟的精确性及科学性。 [1] Shi Zhong, Xiu Qunyang. Ensemble simulations of the urban effect on a summer rainfall event in the Great Beijing Metropolitan Area[J]. Atmospheric Research, 2015,153(3):318-334. [2] Yang Tao, Wang Xiaoyan, Yu Zhongbo, et al. Climate change and probabilistic scenario of streamflow extremes in an alpine region[J]. Journal of Geophysical Research Atmospheres, 2014,119(14):8535-8551. [3] Hesse C, Krysanova V, Stefanova A, et al. Assessment of climate change impacts on water quantity and quality of the multi-river Vistula Lagoon catchment[J]. Hydrological Sciences Journal, 2015,60(5):1-22. [4] Krysanova V, Hattermann F, Huang S, et al. Modelling climate and land use change impacts with SWIM: Lessons learnt from multiple applications[J]. Hydrological Sciences Journal, 2015,60(4):606-635. [5] 王怀志,高玉琴,袁玉,等.基于SWAT模型的秦淮河流域气候变化水文响应研究[J].水资源与水工程学报,2017,28(1):81-87. [6] 宋增芳,曾建军,金彦兆,等.基于SWAT模型和SUFI-2算法的石羊河流域月径流分布式模拟[J].水土保持通报,2016,36(5):172-177. [7] 黄金柏,王斌,温佳伟,等.基于分布式水文模型的阿伦河流域降雨—径流计算[J].水土保持通报,2015,35(1):224-229. [8] Gao Jungang, Sheshukov A Y, Yen Haw, et al. Impacts of alternative climate information on hydrologic processes with SWAT: A comparison of NCDC, PRISM and NEXRAD datasets[J]. Catena, 2017,156:353-364. [9] Ding Jie, Wallner M, Müller H, et al. Estimation of instantaneous peak flows from maximum mean daily flows using the HBV hydrological model[J]. Hydrological Processes, 2016,30(9):1431-1448. [10] 林志强,洪健昌,尼玛吉,等.基于HBV模型的尼洋曲流域上游洪水致灾临界面雨量研究[J].水土保持通报,2016,36(4):22-26. [11] Romagnoli M, Portapila M, Rigalli A, et al. Assessment of the SWAT model to simulate a watershed with limited available data in the Pampas region, Argentina[J]. Science of the Total Environment, 2017,596:437-450. [12] 王强,许有鹏,高斌,等.西苕溪流域径流对土地利用变化的空间响应分析[J].自然资源学报,2017,32(4):632-641. [13] Lu Zhuo, Han Dawei. Misrepresentation and amendment of soil moisture in conceptual hydrological modelling[J]. Journal of Hydrology, 2016,535:637-651. [14] 黄小祥,姚成,李致家,等.栅格新安江模型在天津于桥水库流域上游的应用[J].湖泊科学,2016,28(5):1134-1140. [15] Krysannona V, Wechsung F, Arnold,等.SWIM模型使用指南[M].苏布达,曹丽格,翟建青,等译.北京:气象出版社,2011. [16] 杨志远,高超,臧淑英,等.SWIM模型在东北黑土区流域的适用性评价:以乌裕尔河中上游流域为例[J].地理学报,2017,72(3):457-470. [17] 高超,金高洁.SWIM水文模型的DEM尺度效应[J].地理研究,2012,31(3):399-408. [18] 张淑兰,张海军,王彦辉,等.泾河流域上游景观尺度植被类型对水文过程的影响[J].地理科学,2015,35(2):231-237. [19] 谷一,郝振纯,王国庆,等.HBV模型在逊毕拉河流域的适用性研究[J].水资源与水工程学报,2017,28(1):20-25. [20] 黄清华,张万昌.SWAT模型参数敏感性分析及应用[J].干旱区地理:中文版,2010,33(1):8-15. [21] 丁飞.SWAT模型小尺度流域模拟的适宜性研究:以淮河上游迎河小流域为例[D].南京:南京农业大学,2007.3.3 参数率定的目标函数
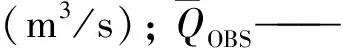

3.4 参数率定结果

3.5 模拟精度评价

4 参数敏感性研究
4.1 thc的敏感性评价


4.2 bff的敏感性评价

4.3 cnum1,cnum3的敏感性评价

4.4 gwq0的敏感性评价
4.5 abf0的敏感性评价


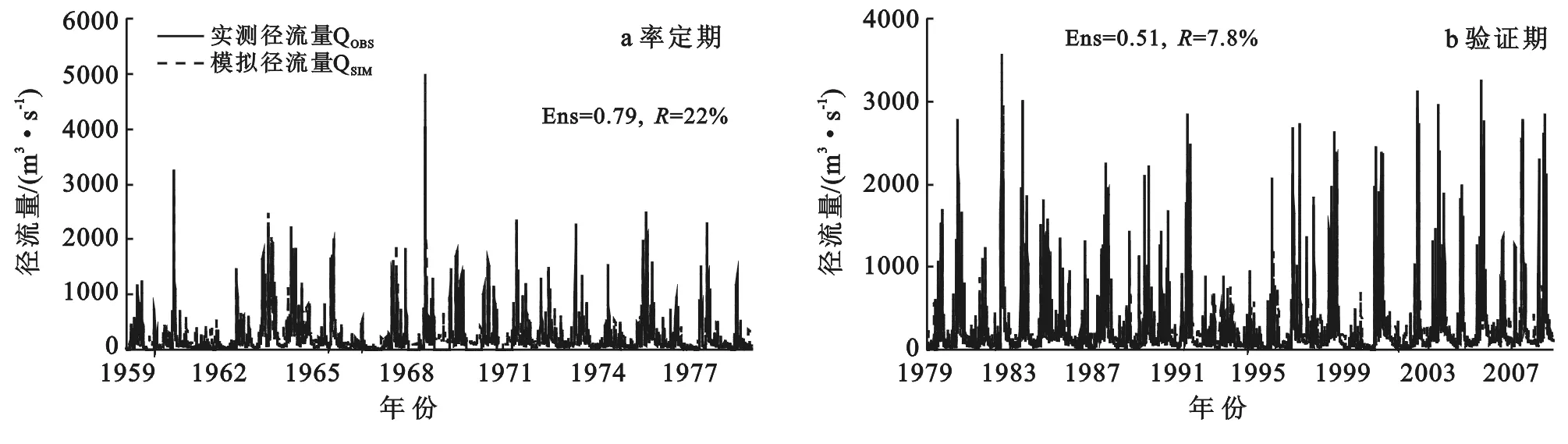
4.6 roc2,roc4的敏感性评价

4.7 sccor的敏感性评价

5 讨论与结论
