基于GWR模型的江西省山洪灾害区域异同性研究
2018-03-29苗月鲜方秀琴吴小君吴陶樱
苗月鲜, 方秀琴, 吴小君, 吴陶樱
(河海大学 地球科学与工程学院, 江苏 南京 211100)
山洪灾害是指山区小流域由暴雨引发的突发性、暴涨暴落的洪水及洪水引发的泥石流、山体滑坡、崩塌等给人民群众带来的灾害[1],其特点是突发性随机性强、历时短、涨幅大、洪峰高、水量集中、成灾迅速、破坏力大[2]。中国山洪灾害频发,尤其是位于中国东南部地区的江西省,属于东亚季风气候,雨量充沛,地形条件复杂,河湖众多,其降水时空分布不均匀,极易形成局部地区强降雨,再加上越来越频繁的人类活动的影响以及灾害性天气多发频发,导致山洪灾害更加频繁,损失和伤亡也更加严重[3]。
目前已经有很多研究表明应用地理加权回归模型(geographically weighted regression, GWR)能更好地解释空间趋势和局部变化情况,并对数据进行分析和解释。GWR在多个领域得到广泛应用,比如:Katarzyna等[4]用GWR方法预测了波罗的海的近底水盐度的空间分布;Sandra Oliveira等[5]利用GWR模型确定影响火灾发生的重要因子,评估因子对火灾发生的影响程度。Park[6]用GWR模型来估计年平均日交通流量,结果表明影响交通流量的因素与年平均日交通流量之间的关系在不同的地区不一样,并用GWR模型预测了不同地区的年平均日交通流量;苏方林[7]通过与其他模型对比发现GWR模型能够更好地反映经济量的空间依赖性;覃文忠等[8]应用GWR方法研究上海市住宅销售平均价格空间分布特征;Huang Jinliang等[9]用GWR估量沿海水域的空间变量与水污染之间的相关关系;Zeng Canying等[10]用GWR预测区域内氮的含量,并制作氮含量空间分布图。然而,就目前而言,利用GWR在山洪灾害空间分布及预测方面的研究还相当少,处于起点阶段,需要进一步的探索。基于此,本研究致力于应用GWR模型探究江西省的山洪灾害的空间分布,揭示不同区域引发山洪的主要原因和造成的灾害程度,以期为实施有效的山洪灾害预防策略和保护策略提供参考依据。
1 数据与研究方法
1.1 研究区概况
江西省河流众多,湖泊水库星罗棋布,有赣江、抚河、信江、饶河和修水五大水系。五大水系均发源于与邻省接壤的边缘山区,从东南西三个方向汇入鄱阳湖,经鄱阳湖调蓄后由湖口汇入长江。因赣江流域面积较广,下垫面变化大,考虑其上下游关系分为3个流域分区,加上环鄱阳湖区域、省界处高山发源的流向其他河流的流域,江西省共分为13个流域。江西省东部的饶河流域往西三面环山,起伏较大;修水流域北面和中部分别为幕阜山和九岭山,地势较高,两条山脉中间形成了河谷;南部的赣江上游流域内多山地,地形起伏比较大。赣东(饶河流域)、赣西(修水流域和赣江下游)和赣南(赣江上游)都是该省极易发生山洪灾害的区域,是山洪灾害重点防治地区,也是山洪灾害调查的重点区域,积累了大量的山洪灾害调查点数据。故本研究选取江西省赣东(饶河流域)、赣西(修水流域和赣江下游)和赣南(赣江上游)3个流域作为研究区。
1.2 数据收集与处理
1.2.1 数据收集
(1) 反应变量。山洪灾害主要是对社会、经济、环境等方面造成的损失[11]。统计不同地区、不同时间发生的山洪灾害情况得到历史山洪灾害灾情,可以反映山洪灾害发生的频率、规模和泛滥范围,较全面的概括这一段时期内山洪灾害的危害程度[12]。根据《山洪灾害技术调查要求》,江西省历史山洪灾害灾情的调查数据有:死亡人数、失踪人数、转移人数、损毁房屋数、直接经济损失。本研究将这几个因子的实际调查数据作为描述山洪灾害危害程度的定量指标,即灾害度指标,作为GWR的反应变量,来探索研究区山洪灾害程度的空间分布规律。
(2) 解释变量。山洪灾害的形成机理复杂,受到多种因素的影响。本研究将这些影响因子分为3类:山洪触发因子、下垫面孕灾环境因子和承灾能力因子。同时解释性变量的选择遵循以下几个原则:目的性、可操作性、简明性、独立性。 ①山洪触发因子。降雨是导致山洪灾害发生的最直接外动力因素,江西省小范围暴雨或局部大暴雨发生概率相对较高,全省80%以上的山洪灾害发生在主汛期4—6月。据统计,江西省实测年最大1 h暴雨量、年最大6 h暴雨量和年最大10 min暴雨量会导致山洪灾害的发生[13]。年降雨量和年暴雨天数也是影响山洪爆发的因素。本文考虑到数据的可获得性和可量化性,选取年最大1 h暴雨量、年最大6 h暴雨量、年最大10 min暴雨量、年降雨量和年暴雨天数5个特征指标作为山洪触发因子。 ②孕灾环境因子下垫面孕灾环境主要指下垫面自然条件,即地形条件。地形是控制山洪泛滥的重要因素,其影响主要表现在高程和坡度2个方面[14]。由于地形指数(TWI)借鉴于Beven 和Kirkby等[15]发展的地形指数模型Topography based hydrological model(TOPMODEL),考虑了地形坡度对产流区形成和变化的影响,其空间分布反映了土壤饱和缺水量的空间分布,具有明确的物理意义。因此,本研究选用高程和TWI作为作为孕灾环境因子。TWI是由公式(1)计算得到:
(1)
式中:α——汇流面积/(hm2);β——坡度(°)。
③承灾能力因子。承灾体的易损性与承灾能力
主要通过人口密度、社会经济发展状况来量化分析[16]。本研究选用GDP和人口密度作为指标。GDP高、人口密度大一方面可能导致该地区受灾程度严重,另一方面,也可能其防洪减灾设施和政策完善,抗灾能力较强。9个影响因子的数据来源如表1所示。
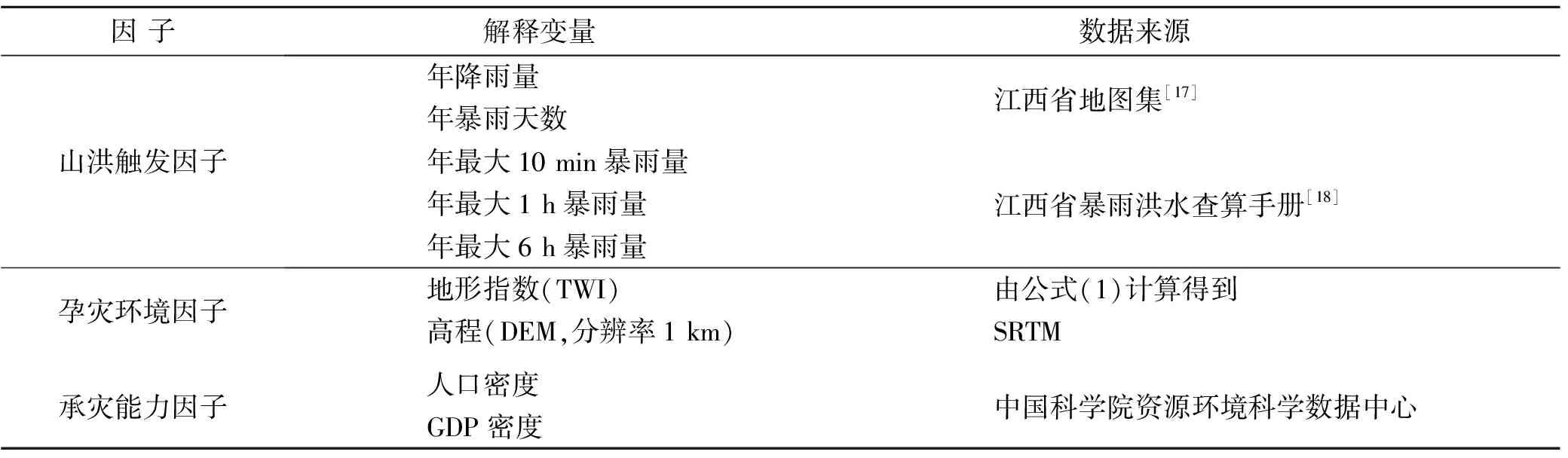
表1 9个解释变量及其数据来源
1.2.2 数据处理 由于选取的各个影响因素取值范围和计量单位存在较大的差别,所以在构建模型前需要进行归一化处理。目的在于消除计量单位的影响并使各指标具有同等的数量级,避免构建模型时可能产生的误差。
在进行归一化处理中,认为年降雨量、年暴雨天数、年最大1 h暴雨量、年最大10 min暴雨量、年最大6 h暴雨量、地形指数、人口密度和GDP等8个影响因素是与山洪灾害的反应变量成线性关系的,因此对于这些影响因素进行归一化处理的公式为:
(2)
式中:xi——归一化前的影响因子数值;Xi——归一化后的影响因子数值;xmin——影响因子的最小值;xmax——影响因子的最大值。
本研究中,历史山洪灾害点的高程值分布的概率密度函数符合偏正态分布,不能简单认为该因子与反应变量是线性相关。因此,我们对高程这个影响因素的归一化按照如下公式进行处理:
x=lg(DEM)
(3)
(4)
式中:x——归一化前高程值;X——归一化后高程值;μ——历史山洪灾害点处高程数据的算术平均值;σ——历史山洪灾害点处高程数据的标准差。
1.3 研究方法
地理加权回归模型(GWR)是近些年发展起来的一种对空间数据进行回归分析的方法,该方法考虑到地理位置邻近的数据具有空间相关性,因此,在传统的多元线性回归方法的基础上,将地理位置嵌入传统的回归模型中。在该模型中,回归系数随地理位置的变化而变化,研究区内有多少个观测点,就将研究区划分为多少个区域,针对每个观测点建立模型,作为该区域的局部回归方程对区域变量进行估计。GWR模型可表示为以下形式:
(i=1,2,…,n)
(5)
式中:(ui,vi)——第i个观测点的坐标;βk(ui,vi)——第i个观测点的第k个回归系数;εi——第i个观测点的随机误差。然后利用局部加权最小二乘方法进行逐点参数估计,各观测点的回归系数是根据距离衰减的一个函数,即对距离函数加权:
(6)
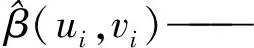
通常选用Gaussian函数作为距离的连续空间权重函数:
(7)
式中:wij——附近点j相对于观测点i的空间权重;dij——j点到i点的距离;b——带宽。带宽是描述权重与距离之间函数关系的一个重要非负参数,带宽的选择很大程度影响模型预测准确程度,通常有最佳固定距离和最佳邻近点数2种形式。带宽的选择通过交叉验证法(Cv)来实现,并通过AIC信息准则(Akaike information criterion)来确定最佳带宽[19]。
GWR结果可以得到模型的决定系数 和解释变量的回归参数,决定系数 代表模型在局部区域的拟合程度,回归参数表示该解释变量对反应变量的影响程度。以此来探测空间关系的非平稳性,揭示研究区重要性变量的分异性。该方法非常适用于具有空间异质性的空间数据的建模[8,20]。在构建GWR模型时,并不是解释变量越多越好,一些解释变量加入回归模型后反而会使模型的拟合精度下降,因此要选用适宜的解释变量使得模型拟合精度最优。
2 结果与分析
本次研究,首先利用ArcGIS中模型空间关系模块对9个解释变量进行共线性检验,即对解释变量进行方差膨胀因子(VIF)检验,剔除掉VIF>5的解释变量,因为VIF>5很有可能是变量间共线性出现的触发点[21]。对3个研究分区的9个初始解释变量进行VIF检验,发现赣东地区VIF>5的变量为年最大10 min降雨量的,应予以剔除;赣西地区无VIF>5的变量,因此9个初始解释变量之间不存在共线性关系;在赣南地区,年暴雨天数和年降雨量的VIF>6,年最大6 h降雨量VIF>5,剔除年暴雨天数和年降雨量后,剩余的解释变量的VIF值都小于5。然后用GWR 4.0软件分别对3个研究分区的每个灾害度指标构建GWR模型,所得模型的解释变量组合及拟合精度如表2。
由表2可知,赣东地区的死亡人口调查数据全为0,而赣南地区的死亡人口、转移人口和损毁房屋的调查数据值的数量级跨度非常大,出现异常值,因此这些灾害度指标无法构建模型。最后利用GIS工具箱制作各区域不同灾害度指标的空间分布图。本文从同一区域不同灾害度指标建模、不同区域同一灾害度指标建模和不同灾害度指标空间分布3个方面来进行探讨,对比各GWR模型之间的差异,分析讨论造成这种差异的原因。

表2 江西省灾害度指标构建的GWR模型组合及精度对比
2.1 同一区域不同灾害度指标建模
表2的纵向比较反映的是同一研究区域不同灾害度指标建模的异同。根据表2,无论在哪个区域,所有的灾害度指标都受到山洪触发因子的影响,但具体是山洪触发因子中的哪些解释变量影响灾害度指标存在差异。在赣东地区,转移人口与损毁房屋有相同的山洪触发因子,即年暴雨天数;转移人口与直接经济损失也有相同的山洪触发因子,即年最大6 h暴雨量;死亡人口和转移人口涉及到承灾体,因此人口密度也是影响这2个灾害度指标的有效解释变量,而GDP也是影响死亡人口的其中一个因素。在赣西地区,失踪人口、转移人口、损毁房屋和直接经济损失有相同的山洪触发因子,即年最大10 min暴雨量;死亡人口、失踪人口、转移人口和损毁房屋受到承灾能力因子中人口密度的影响,说明在该地区人口密度比人均GDP对模型结果的影响更大;死亡人口、转移人口、损毁房屋和直接经济损失都受到孕灾环境因子的影响,其中转移人口同时受到DEM和TWI这2个孕灾环境因子的影响,死亡人口和损毁房屋只受到DEM的影响,直接经济损失只受到TWI 的影响。这些模型中转移人口模型的解释变量数量最多,有7个,且拟合精度最高,达到0.920 2。在赣南地区,失踪人口与直接经济损失模型没有相同的山洪触发因子,失踪人口还同时受到2个孕灾环境因子的影响。
综上所述,5个灾害度指标的建模存在共性,即同一区域不同灾害度指标构建的模型都包含山洪触发因子,说明无论描述山洪灾害度的指标是什么,降雨条件都是导致山洪灾害发生的最主要因素。同时,5个灾害度指标的建模也存在差异性:在赣东地区,孕灾环境因子和承载能力因子对有的灾害度指标有影响,对有的灾害度指标影响不明显,有时甚至会使模型整体拟合精度降低;在赣西地区,在5个描述降雨的山洪触发因子中,对不同灾害度指标有影响的解释变量不同数量也不同,孕灾环境因子和承灾能力因子中的人口密度也是造成山洪灾害的重要原因;在赣南地区,失踪人口和直接经济损失量模型的影响因子包含了不同的山洪触发因子,而死亡人口还受到地形因子的影响。
2.2 不同区域同一灾害度指标建模
表2的横向比较反映的是不同区域同一灾害度指标建模的异同。根据表2,无论灾害度指标是什么,所有地区都受到山洪触发因子的影响,但具体是山洪触发因子中的哪些解释变量影响灾害度指标存在差异。当灾害度指标为死亡人口时,赣东和赣西地区都受到承灾能力因子人口密度的影响,赣东地区还受到GDP的影响,赣西地区受到地形条件DEM的影响。当灾害度指标为失踪人口时,赣西地区受到承灾因子人口密度的影响,而赣南地区同时受到2个孕灾环境因子TWI和DEM的影响。当灾害度指标为转移人口时,赣东和赣西地区有人口密度和年最大6 h暴雨量2个共同的解释变量,赣西地区还同时受到2个孕灾环境因子DEM和TWI的影响。当灾害度指标为损毁房屋时,赣东地区只包含了一个山洪触发因子年暴雨天数,而赣西地区同时受到山洪触发因子、孕灾环境因子和承灾能力因子的影响。当灾害度指标为直接经济损失时,赣东和赣南地区都受到一个相同的山洪触发因子年最大6 h暴雨量的影响,但拟合精度不同,而赣西地区还受到孕灾环境因子TWI的影响。
综上所述,3个研究区的建模存在共性,即不同区域同一灾害度指标构建的模型都包含山洪触发因子,说明不论在哪个区域,降雨条件都是导致山洪灾害发生的最主要因素。同时,3个研究区的建模也存在差异性:当灾害度指标为死亡人口时,赣东和赣西的模型有相同承灾能力因子,赣西的模型还包含孕灾环境因子;当灾害指标为失踪人口时,赣西的模型受到承灾能力因子的影响,而赣南的模型受到孕灾环境因子的影响;当灾害度指标为转移人口时,赣东和赣西的模型有相同的承灾能力因子和山洪触发因子,两个地区的模型包含的其他山洪触发因子有差异,赣西的模型还受到孕灾环境因子的影响;当灾害度指标为损毁房屋时,赣东的模型只包含一个山洪触发因子,赣西的模型除了山洪触发因子还受到孕灾环境因子和承灾能力因子的影响;当灾害度指标为直接经济损失时,赣东和赣南的模型有且只有一个相同的山洪触发因子,但模型的精度也不同,而赣西的模型还受到孕灾环境因子的影响。
2.3 不同区域山洪灾害度指标的空间分布
本文对每个区域的每个灾害度指标都构建了合适的模型,然后利用这些模型对无实地调查数据的地区进行预测。由于GWR模型得到的局部拟合精度变化范围较大,有些地区得到的预测结果不可靠,即出现超出正常范围的偏大或偏小现象,因此本文结合实际情况对预测结果数据进行剔除,使得数据能有效反映灾害度指标的空间分布情况。
在赣东地区,死亡人口、转移人口、损毁房屋和直接经济损失4个灾害度指标的值普遍在东部较低,在西北方向受灾程度偏大,原因是饶河流域东部为平原地区,地势平坦,往西三面环山,起伏较大,当有较大的降雨、暴雨时,容易形成山洪造成损失。但是当灾害度指标不同时,受灾严重的地区分布存在明显的差异:死亡人口较多的地方主要在婺源县北部、乐平市西部、波阳县南部和德兴市东部,转移人口较多的地方主要在乐平市和景德镇市,波阳县南部也有较多的人口转移,损毁房屋严重的地方主要在景德镇市,在浮梁县、婺源县和德兴市也有少数村落的房屋损毁严重。
在赣南地区,失踪人口较多的地区主要集中在该流域中心即甘心和于都县,而直接经济损失较严重的地区在该区崇义县西部、上犹县西部和信丰县北部。该流域内多山地,地形起伏比较大,且分布没有明显的规律,流域北部地区暴雨量相对南部较大,因此该地区不同指标受灾程度差异性较大。
在赣西地区,由修水流域和赣江下游两部分组成,修水流域北面和中部分别为幕阜山和九岭山,地势较高,两条山脉中间形成了河谷,东南部地区的降雨丰沛,因此该流域的山谷地带和东南地区容易形成山洪灾害,而赣江下游东部为平原地区,西北为九岭山脉,西南有武山,从西往东地形指数逐渐增大,年降雨量从西北到东南呈递减趋势,且暴雨中心都分布在流域的北部,因此在该流域北部和九岭山的南面容易形成山洪灾害。因此,受灾较严重的地区分布在修水流域东部和赣江下游西北部。但是,每个灾害度指标受灾严重地区的分布存在差异:死亡人口较多的地方在铜鼓县和万载县北部,失踪人口多的地方主要在铜鼓县和修水县南部,转移人口较多的地方在铜鼓县南部和高安市南部,宜春市、上高县和万载县有少部分地区需要人口较多,损毁房屋严重的地区主要分布在铜鼓县、新干县和万载县北部,直接经济损失严重的地区安义县和宜春市北部,高安市和铜鼓县的损失比较严重。
同一地区,当灾害度指标不同时,受灾程度的分布情况存在差异:一些行政区在多个灾害度指标中都呈现出比较严重的受灾程度,例如景德镇市在转移人口、损毁房屋和直接经济损失中的受灾程度都严重;乐平市在死亡人口、转移人口和直接经济损失中的受灾程度严重;铜鼓县在死亡人口、失踪人口、转移人口和损毁房屋中的受灾程度严重。一些行政区虽然在多个灾害度指标中都呈现出严重的受灾程度,但是由于灾害度指标不同,受灾严重的地方在该行政区的地域分布不同,例如万载县死亡人口多和损毁房屋严重的地方都在该县北部,转移人口较多的地方在该县的北方和西南角,直接经济损失严重的地区在该县西南角;高安市的转移人口较多的地区在该市南部,直接经济损失严重的地区在该市东北部。其他的行政区只在其中一个灾害度指标中有严重的受灾现象。
3 结 论
通过GWR对江西省赣东、赣西和赣南3个研究区的5项山洪灾害度指标构建模型,并将该模型应用到无实地调查数据的地区,并分别将这几项山洪灾害指标的空间分布进行制图,使我们更加直观的了解山洪灾害的空间分布情况,更加清楚地反映江西省不同研究区山洪灾害的空间分布规律以及差异。
结果表明,不同地区构建的模型有不同的共线性因子,所有构建的模型都有山洪触发因子,虽然不同的模型中表述山洪触发因子的解释变量及其数量有差异,但降雨是诱发山洪灾害的最主要因素;同一地区不同灾害度指标构建的模型之间和不同地区同一灾害度指标构建的模型之间都有共性和差异性。在其中任一条件下,一些模型会存在相同的解释变量,也有一些模型的解释变量完全不同;受灾严重的地区都集中分布在容易形成山洪的地区,该地区通常地形起伏较大,降雨量也大。但当灾害度指标不同时,受灾程度的具体分布情况存在明显差异。
因此,在构建各项灾害度指标模型时,不仅要考虑到地域上的差异,也要考虑到不同灾害度指标之间的差异,GWR能有效地解释局部空间变化情况和重要解释变量的分异性。而好的模型能详细准确的描述灾害度指标的空间分布情况,为行政区域综合灾害度评估提供基础数据,为抗洪救灾时资源以及人力的分配提供参考,帮助人们规划设置避灾的工程措施和非工程措施提供依据,同时也为政府对各分区的监测和管理提供重要决策支持。
[1] 许小华,何雯.基于土地利用分析的山洪灾害危险等级划分研究[J].江西水利科技,2015,41(4):283-290.
[2] 刘志雨.山洪预警预报技术研究与应用[J].中国防汛抗旱,2012,22(2):41-45.
[3] 李明辉,熊剑英.江西省山洪灾害防治规划概述[J].江西水利科技,2005,31(2):73-77.
[4] Lukawska-Matuszewska K, Urbański J A. Prediction of near-bottom water salinity in the Baltic Sea using Ordinary Least Squares and Geographically Weighted Regression models[J]. Estuarine Coastal and Shelf Science, 2014,149:255-263.
[5] Oliveira S, Pereira J M C, San-Miguel-Ayanz J, et al. Exploring the spatial patterns of fire density in Southern Europe using geographically weighted regression[J]. Applied Geography, 2014,51:143-157.
[6] Park N. Estimation of average annual daily traffic(AADT)using geographically weighted regression(GWR) method and geographic information systems[D]. Florida: Florida International University, ProQuest Dissertations Publishing, 2004.
[7] 苏方林.基于地理加权回归模型的县域经济发展的空间因素分析:以辽宁省县域为例[J].学术论坛,2005(5):81-84.
[8] 覃文忠,王建梅,刘妙龙.地理加权回归分析空间数据的空间非平稳性[J].辽宁师范大学学报:自然科学版,2005,28(4):476-479.
[9] Huang Jinliang, Huang Yaling, Pontius R G, et al. Geographically weighted regression to measure spatial variations in correlations between water pollution versus land use in a coastal watershed[J]. Ocean & Coastal Management, 2015,103(103):14-24.
[10] Zeng Canying, Yang Lin, Zhu Axing, et al. Mapping soil organic matter concentration at different scales using a mixed geographically weighted regression method[J]. Geoderma, 2016,281:69-82.
[11] 孙厚才,沙耘,黄志鹏.山洪灾害研究现状综述[J].长江科学院院报,2004,21(6):77-80.
[12] 唐川,朱静.基于GIS的山洪灾害风险区划[J].地理学报,2005,60(1):87-94.
[13] 刘少军,张京红,张明洁,等.海南岛山洪灾害风险区划研究[J].水土保持研究,2013,20(5):165-169.
[14] 许小华,何雯.基于DEM的山洪灾害风险区划分研究[J].中国农村水利水电,2015(10):83-86.
[15] 邓慧平,李秀彬.地形指数的物理意义分析[J].地理科学进展,2002,21(2):103-110.
[16] 哈斯塔木嘎,蔡云松,石力伟.基于GIS的暴雨山洪气象灾害风险评估[J].现代农业科技,2013(18):240-241.
[17] 《江西地图集》编纂委员会.江西省地图集[M].北京:中国地图出版社,2008.
[18] 江西省水文局.江西省暴雨洪水查算手册(2010版)[EB/OL].(2013-04-19)[2015-07-16]. http://www. bzfxw. com/soft/sort011/ShuiLi/168219063. html.
[19] 覃文忠.地理加权回归基本理论与应用研究[D].上海:同济大学,2007.
[20] 郭含茹,张茂震,徐丽华,等.基于地理加权回归的区域森林碳储量估计[J].浙江农林大学学报,2015,32(4):497-508.
[21] 王旭,林征,张志,等.基于GWR模型的北极滨海平原融冻湖表面温度空间分布模拟[J].武汉大学学报:信息科学版,2016,41(7):918-924.
