基于MATLAB的微波加热腔内介质扰动下的数值模拟研究*

汪维军，林 欢，陈 华,2

(1.昆明理工大学 理学院，云南 昆明 650500；2.昆明理工大学 非常规冶金省部共建教育部重点实验室，云南 昆明 650093)

20世纪60年代末，微波加热在生物医学工程、食品工业和橡胶工业中首先获得成功应用，如今，微波加热已经成为一种新兴的加热技术，并在冶金、材料、化学和能源等诸多领域受到越来越广泛的关注[1-2]，而电磁性能的改变对物料吸收微波能力、效果也有着明显的影响[3]；因此，研究腔体内的电磁特性对微波加热至关重要。1996年，Yee提出了时域有限差分法(Finite Difference Time Domain，FDTD)[4-5]，作为时域方法中最为经典的算法，该方法以其原理直观、编程简单和实用性强等特点，成为了一种典型的全波分析方法，一直在时域方法中占主导地位，在计算电磁学领域内被广泛、深入地研究，极大地推动了整个时域方法的发展[6]。FDTD法直接将有限差分式代替Maxwell旋度方程中的微分式，得到关于场分量的有限差分式，用具有相同电参量的空间网格去模拟研究体，选取合适的场初值和计算空间的边界条件，进行求解[7-9]。戴国强等[10]通过对完美匹配层边界条件的设置，应用MATLAB软件对自由空间散射场进行了仿真，解决了电磁场散射等问题，给出了在不同时间步下的仿真结果。王立[11]基于MATLAB软件，采用时域有限差分法对二维TM波在空间的传播进行了仿真，得到了电磁波在整个区域里面的动态传播，以便直观、清楚地观察电磁场的分布情况。本文应用MATLAB软件对波导和谐振腔内电磁波和其能量分布进行了模拟，同时也对此腔体内不同介质下的电磁场进行了仿真，进而得到了不同条件下传输波导的最好匹配频率。

1 时域有限差分法(FDTD)的基本原理

FDTD算法将Maxwell旋度方程组进行时间和空间的离散，得到递推的差分方程[12]，用差分方程的解近似代替原方程的解。在求解过程中，需要保证方程组解的收敛性和稳定性。对于无源的空间，在直角坐标系下，当μ、ε、σe和σm不是时间的函数时，Maxwell方程可以分解为6个标量方程。K. S. Yee在对这2组标量方程进行差分离散时的巧妙之处，就在于Yee网格的提出及在时间和空间上同时对6个电场和磁场分量进行差分，其结果就是使得电场和磁场在时间和空间上都相差半个网格。Yee网格如图1所示。

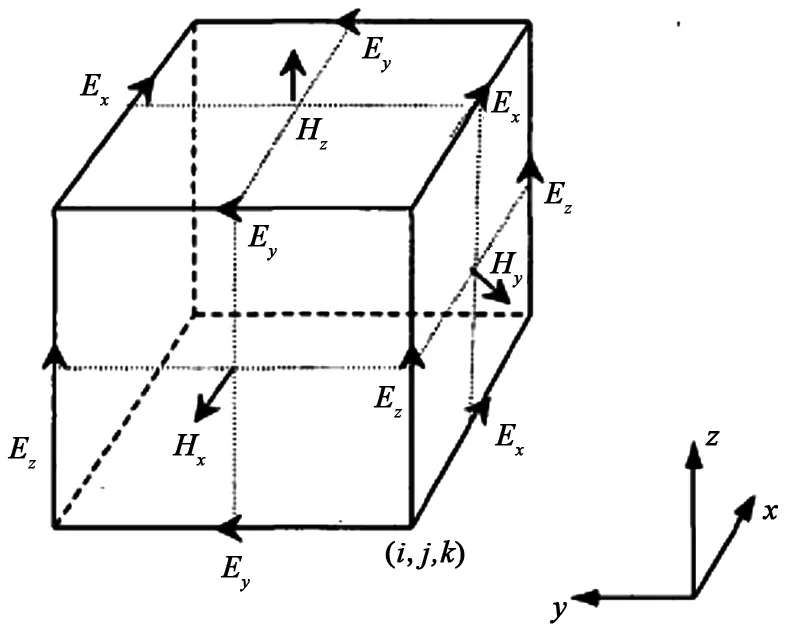
图1 FDTD离散中的Yee元胞

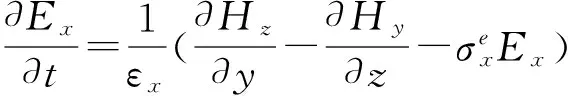
(1)

(2)

(3)

(4)

(5)

(6)

式中，Ex、Ey、Ez为电场强度；Hx、Hy、Hz为磁场强度；μ为媒质的磁导率；ε为介电常数；σe和σm分别为媒质的电损耗和磁损耗。

根据Yee提出的元胞原理，将式1进行离散得到：

(7)

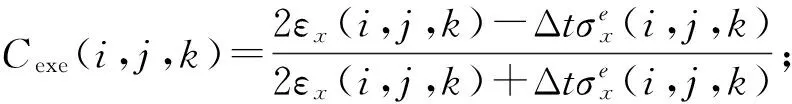
Δx、Δy和Δz为空间步长；Δt为时间步长。

2 FDTD中的激励源

用FDTD方法分析电磁问题时一个重要的任务是对激励源的模拟，即选择合适的入射波形式以及用适当的方法将入射波加入到FDTD迭代中。本文选取的是微分高斯脉冲，将高斯脉冲求导后得到的微分高斯脉冲函数如下：

(8)

其优点是不含零频率分量，频域形式为：

(9)

当以微分高斯脉冲为入射波时，如果关心的频谱范围的最高频率为fmax，则对应的真空波长为λmin(λmin=c/fmax，c为自由空间波速)。若FDTD的Yee元胞尺寸取为σ=λmin/N，其中N≥10，且取时间间隔为Δt(Δt=σ/(2c))，则有：

(10)

若脉冲宽度为τ，则在1个脉冲时间内，应至少取采样点总数Nτ为：

(11)

3 吸收边界条件

自从Yee提出FDTD方法以来，吸收边界条件的研究就一直没有停止过。目前，吸收边界条件主要有2种：一种是在边界上引入吸收材料，电磁波在无反射地进入吸收材料后被衰减掉，如PML(Perfectly Matched Layer)，这种方法构造复杂，内存需求较大，但在很大的入射角度上吸收效果较好；另一种是从外行波方程出发构造的透射边界条件，如Mur边界条件等，这种类型的透射边界条件具有构造简单、内存需求小和基本上不额外消耗内存等特点。

由于计算机的局限性，基于有限差分的电磁数值模拟只能在有限区域内进行，这样必须对计算区域的边界进行截断处理[13]，各向异性介质完全匹配层(Uniaxial PML，UPML)边界条件不需要对场分量进行分裂，迭代公式简单，便于程序实现[14]，且UPML对各频段电磁波的吸收具有比较好的稳定性[15]；因此，本文中将会用到UPML吸收边界条件、各向异性介质麦克斯韦旋度方程(无源)在时谐场情形时为：

▽×H=jωε·E
▽×E=-jωμ·H

(12)

为便于得到时间推进式，引入中间变量D、B，经过推导便能得到截断绝缘介质的UPML三维时域方程，其时间推进步骤为H→D→E→B→H，截断绝缘介质的UPML三维FDTD的推导及公式参见文献[16]。

推导出FDTD的更新方程后，可以构造出时间步进算法。MATLAB程序流程图如图2所示。

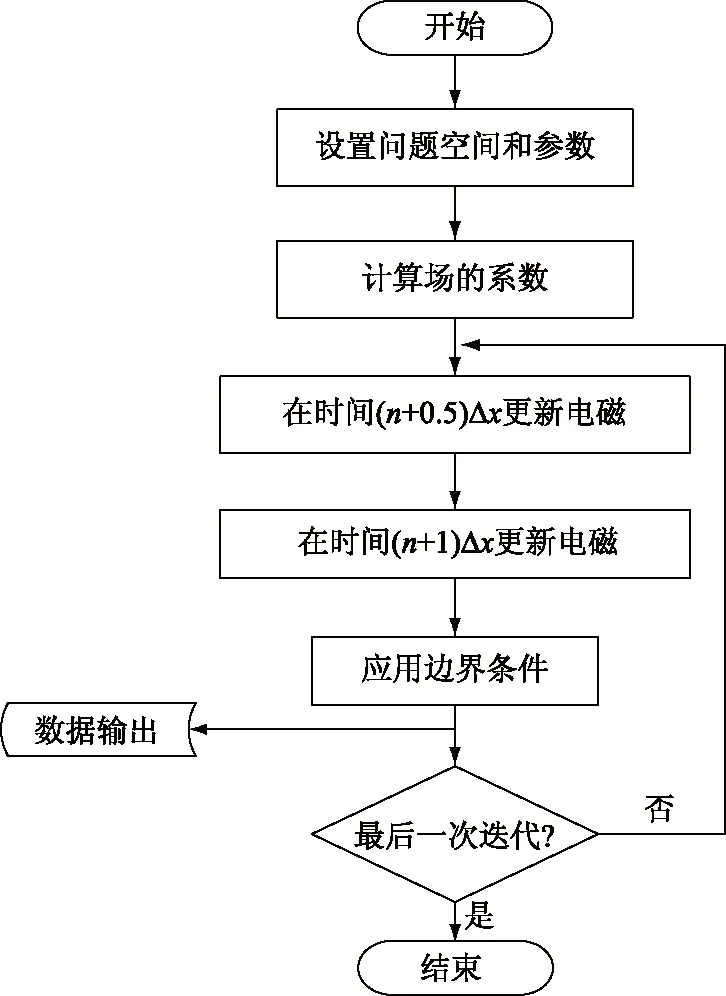
图2 FDTD算法流程图

4 数值算例

以X波段WR90矩形波导为例(见图3)，其宽为22.86 mm，高为10.16 mm，模式的理论截止频率为6.562 GHz。应用MATLAB软件仿真时，使用UPML吸收边界条件截断矩形波导的两端，其他的四边用PEC截断。矩形波导在横截面上划分为24×12个网格，而在传播方向上大约划分为60个网格。

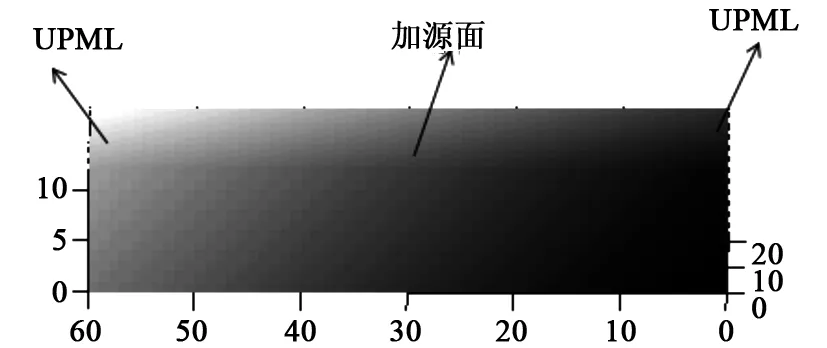
图3 X波段WR90矩形波导

应用MATLAB软件对该矩形波导的TE10模式的波阻抗进行仿真，得到波阻抗与频率的关系，将得到的结果与文献[17]中用FDTD仿真该矩形波导的结果进行比较，结果如图4所示。从图4中可以看出，随着频率的增大，波阻抗先增大后减小，当达到最大时，截止频率为6.56 GHz。2种仿真的结果与理论结果一样，说明此MATLAB程序的正确性。

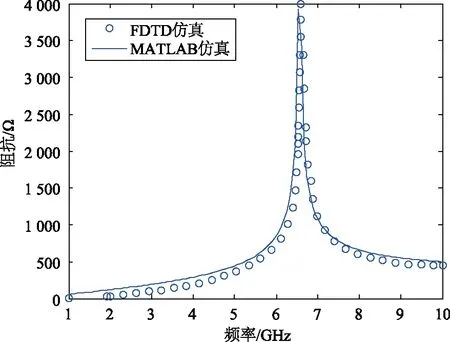
图4 X波段WR90矩形波导的波阻抗

本文研究的模型如图5所示。该模型由谐振腔和传输波导组成。其中，谐振腔的长、宽、高尺寸分别为200、100和100 mm，传输波导为BJ—26型波导，其长、宽、高尺寸分别为43、140和22 mm。采用的激励源为微分高斯脉冲源，中心频率为2.45 GHz。为建模方便，采用等间隔离散Δx=Δy=Δz=Δ=2 mm，时间步长Δt=Δ/(2c)。激励源从x-o-z面处馈入，仿真步长Δt=2 000时，应用MATLAB软件，仿真得到真空下腔体内部电场分布图如图6所示。

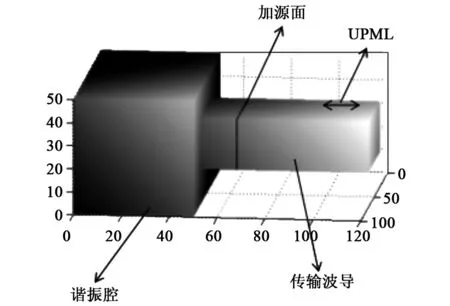
图5 波导加载谐振腔结构的FDTD设置

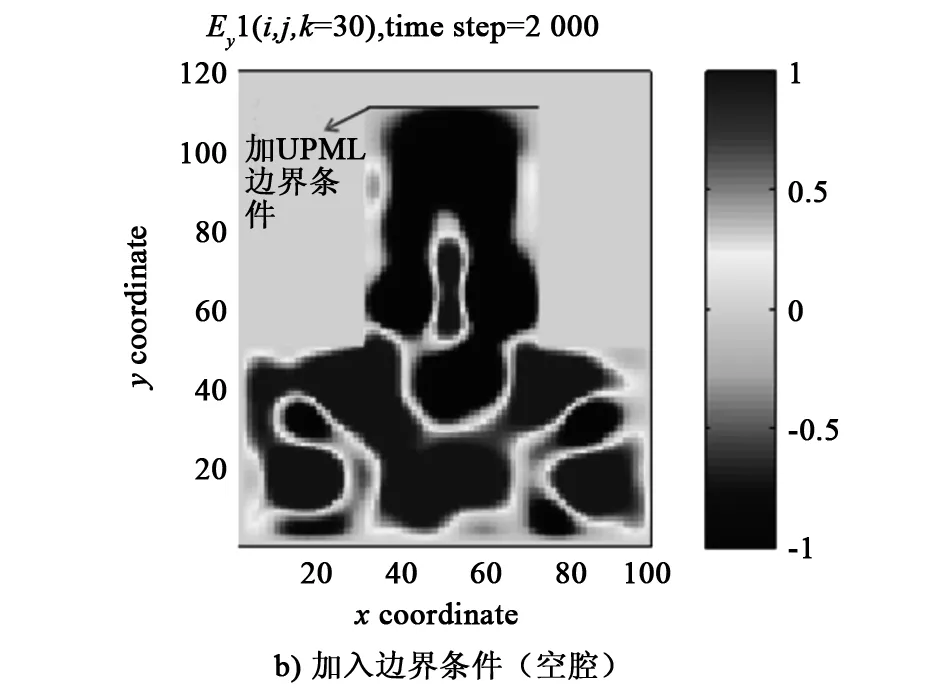
图6 真空下腔体内部电场分布图

图6a为未加入UPML边界条件，Ey在z=30σ平面内，Δt=2 000时刻的分布图；图6b为加入UPML边界条件Ey在z=30σ平面内，Δt=2 000时刻的分布图。从图6a可以看出，无边界条件下电磁场在边界上有反射，腔内的电场比较强；由图6b可知，加入UPML边界条件后，在该边界处电磁波不再向前传播，而是全部被吸收，腔体内电场比较弱，没有明显的反射，表明UPML层的吸收效果较好。

上述研究了空腔下电磁场的分布，但是在大多数情况下，所面对的腔体里是充满介质的，因此，本文分别采用干燥的木头(εr=3)和石英(εr=5)[18]对腔体进行填充，应用MATLAB软件进行仿真，得到在不同介质、相同时间步、同一截面处电场的分布情况(见图7)。

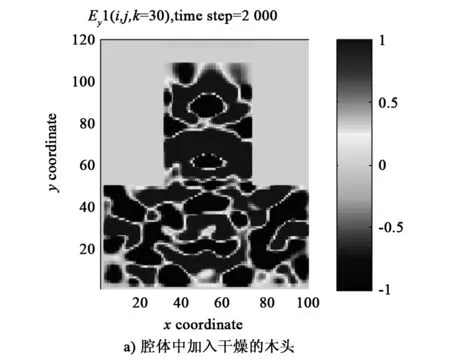
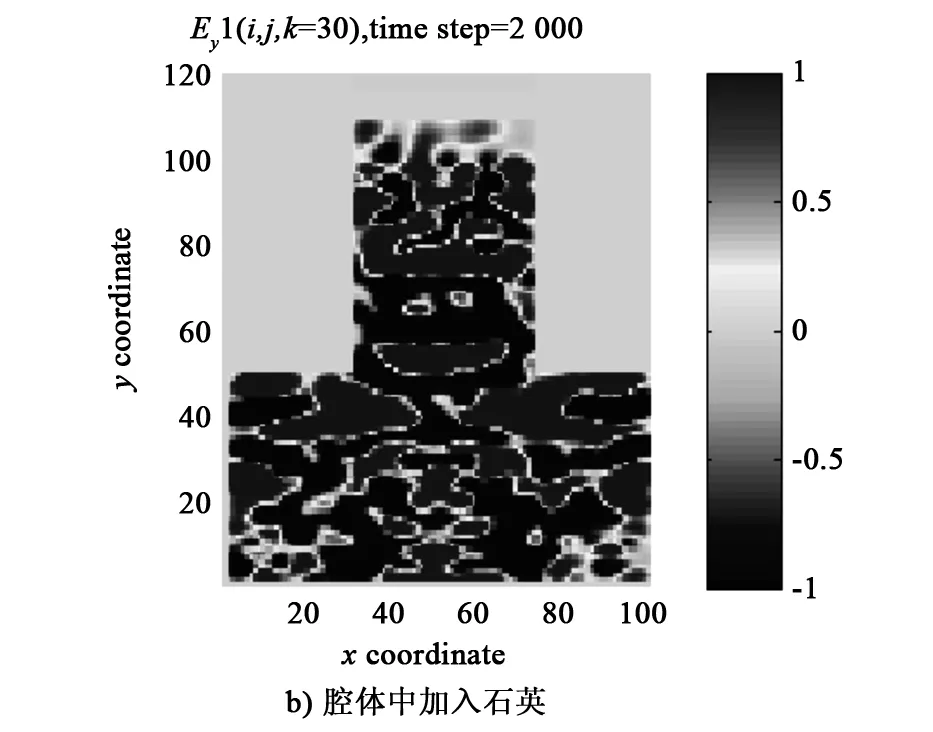
图7 不同介质、相同时间步、同一截面处电场的分布图

从图7可以看出，在同一时刻，在其他条件不变的情况下，随着腔体内所加介质相对介电常数的增大，其腔体内的电场分布越均匀，从而反映出该介质对电磁波的吸收效果越好。在该模型加入UPML边界条件，腔体内分别填充真空、干燥的木头和石英介质的条件下，可以得到y方向上同一截面处的s参数。当运行时间为2 000时间步，腔体内分别为真空、干燥的木头和石英介质时，传输波导在y方向同一截面处的s11参数(即反射参量)如图8所示。

从图8中可以看到，s11在不同的介质中有所不同：在空腔下匹配最好时的幅度值为-5 dB，频率为2.42 GHz；加入干燥的木头时的幅度值为-6.5 dB，频率为2.35 GHz；加入石英时幅度值为-7.08 dB，频率为2.41 GHz。说明随着腔体内填充介质的相对介电常数的增大，吸收电磁波的效果增强。虽然在模拟中应用了UPML吸收边界条件，但是在仿真中存在频差或者也有可能引入了其他的误差，所以，在不同的介质下达到最佳匹配时的频率与理论上相比存在偏差。

5 结语

利用时域有限差分法，在单一激励源的条件下，对传输波导和谐振腔内电磁场的分布进行了模拟。首先利用求矩形波导的波阻抗对程序进行了验证；其次分别在传输波导是否加边界条件的情况下，对波导内同一平面处的电磁波做了比较；最后在腔体内填充了不同的介质，进而得到了在不同的条件下腔体内的电磁场的分布、电介质对电磁波传播的影响以及在同一截面处的散射参量。

[1] 胡兵，黄柱成，王华. 铁及其氧化物在微波场中的升温特性[J]. 中南大学学报：自然科学版，2013, 44(8):3095-3101．

[2] 刘宏强，魏贤智，李飞，等. 基于射频隐身的雷达跟踪状态下单次辐射能量实时控制方法[J]. 电子学报，2015,43(10):2047-2052．

[3] Yee K S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media[J]. IEEE Trans. Antennas Propagat., 1966, 14:302-307.

[4] 王长清，祝西里. 电磁场中的时域有限差分法[M]. 北京：北京大学出版社，1994.

[5] 杜磊. 时域有限元电磁计算方法的研究[D]. 南京：南京理工大学，2009.

[6] Jha A K, Akhtar M J. A generalized rectangular cavity approach for determination of complex permittivity of materials[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(11):2632-2641.

[7] Guo W H, Li W J, Huang Y Z. Computation of resonant frequencies and quality factors of cavities by FDTD technique and Padé approximation[J]. IEEE Microwave and Wireless Components Letters, 2001, 11(5):223-225.

[8] Oskooi A F, Roundy D, Ibanescu M, et al. MEEP:A flexible free-software package for electromagnetic simulations by the FDTD method[J]. Computer Physics Communications, 2010, 181(3):687-702.

[9] 潘小娟，陈津，张猛，等. 微波加热含碳碳酸锰矿粉升温机理[J]. 中南大学学报：自然科学版，2008, 39(6):1233-1238．

[10] 戴国强，余震虹. 时域有限差分方法的研究[J]. 现代电子技术，2013, 36(1):140-143.

[11] 王立. 时域有限差分法仿真二维电磁波传播[J]. 舰船科学技术，2011, 33(2):49-52.

[12] Elsherbeni A, Demir V. MATLAB模拟的电磁学时域有限差分法[M]. 喻志远，译. 北京：国防工业出版社，2013.

[13] 姜彦南，等. 瞬变电磁场模拟的CPML吸收边界条件[J]. 计算物理，2015, 32(6):701-708.

[14] 魏丽君，张彬，张若冰. UPML吸收边界条件的无截断数值模拟[J]. 数学的实践与认识，2016, 46(6):254-260.

[15] 于涛，戚宗锋，李志鹏. 时域有限差分法常用吸收边界的性能分析[J]. 海军航空工程学院学报，2016, 31(5):506-512.

[16] 葛德彪，闫玉波. 电磁波时域有限差分方法[M]. 3版. 西安：西安电子科技大学出版社，2011.

[17] 杨儒贵. 高等电磁场理论[M]. 北京:高等教育出版社，2008.

[18] 谢处方，饶克谨. 电磁场与电磁波[M]. 4版. 北京：高等教育出版社，2006.